Логарифмические уравнения и неравенства
Логарифмическим уравнениям и неравенствам в вариантах ЕГЭ по математике посвящена задача C3. Научиться решать задания C3 из ЕГЭ по математике должен каждый ученик, если он хочет сдать предстоящий экзамен на «хорошо» или «отлично». В данной статье представлен краткий обзор часто встречающихся логарифмических уравнений и неравенств, а также основных методов их решения.
Итак, разберем сегодня несколько примеров логарифмических уравнений и неравенств, которые предлагались учащимся в вариантах ЕГЭ по математике прошлых лет. Но начнет с краткого изложение основных теоретических моментов, которые нам понадобятся для их решения.
Логарифмическая функция
Определение
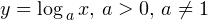
называют логарифмической функцией.
Основные свойства
Основные свойства логарифмической функции y = loga x:
| | a > 1 | 0 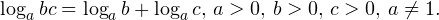 0,\, b>0,\, c>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/> 0,\, b>0,\, c>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>• Логарифм частного двух положительных чисел равен разности логарифмов этих чисел:
• Если a и b — положительные числа, причем a ≠ 1, то для любого числа r справедливо равенство:
• Если a, b, c — положительные числа, причем a и c отличны от единицы, то имеет место равенство (формула перехода к новому основанию логарифма):
Решение логарифмических уравнений и неравенствПример 1. Решите уравнение: Решение. В область допустимых значений входят только те x, при которых выражение, находящееся под знаком логарифма, больше нуля. Эти значения определяются следующей системой неравенств:
С учетом того, что получаем промежуток, определяющий область допустимых значений данного логарифмического уравнения: На основании теоремы 1, все условия которой здесь выполнены, переходим к следующему равносильному квадратичному уравнению: В область допустимых значений входит только первый корень. Ответ: x = 7. Пример 2. Решите уравнение: Решение. Область допустимых значений уравнения определяется системой неравенств:
Очевидно, что эти два условия противоречат друг другу. То есть нет ни одного такого значения x, при котором одновременно выполнялись бы оба неравенства. Область допустимых значений уравнения является пустым множеством, а значит решений у данного логарифмического уравнения нет. Ответ: корней нет. Обратите внимание, что в этом задании нам вообще не пришлось искать корни уравнения. Достаточно оказалось определить, что его область допустимых значений не содержит ни одного действительно числа. Это одно из преимуществ такой последовательности решения логарифмических уравнений и неравенств (начинать с определения области допустимых значений уравнения, а затем решать его путем равносильных преобразований). Примет 3. Решите уравнение: Решение. Область допустимых значений уравнения определяется здесь легко: x > 0. Уравнение принимает вид: Оба ответа входят в область допустимых значений уравнения, поскольку являются положительными числами. Пример 4. Решите уравнение: Решение. Вновь начнем решение с определения области допустимых значений уравнения. Она определяется следующей системой неравенств:
Воспользовавшись правилом сложения логарифмов, переходим к равносильному в области допустимых значений уравнению: Основания логарифмов одинаковы, поэтому в области допустимых значений можно перейти к следующему квадратному уравнению: Первый корень не входит в область допустимых значений уравнения, второй — входит. Ответ: x = -1. Пример 5. Решите уравнение: Решение. Будем искать решения в промежутке x > 0, x≠1. Преобразуем уравнение к равносильному: Оба ответа входят в область допустимых значений уравнения. Пример 6. Решите уравнение: Решение. Система неравенств, определяющая область допустимых значений уравнения, имеет на этот раз вид: Используя свойства логарифма, преобразуем уравнение к равносильному в области допустимых значений уравнению: Используя формулу перехода к новому основанию логарифма, получаем: В область допустимых значений входит только один ответ: x = 4. Перейдем теперь к логарифмическим неравенствам. Это как раз то, с чем вам придется иметь дело на ЕГЭ по математике. Для решения дальнейших примеров нам потребуется следующая теорема: Теорема 2. Если f(x) > 0 и g(x) > 0, то: Решение. Начнем с определения области допустимых значений неравенства. Выражение, стоящее под знаком логарифмической функции, должно принимать только положительные значения. Это значит, что искомая область допустимых значений определяется следующей системой неравенств:
Так как в основании логарифма стоит число, меньшее единицы, соответствующая логарифмическая функция будет убывающей, а потому равносильным по теореме 2 будет переход к следующему квадратичному неравенству: Окончательно, с учетом области допустимых значений получаем ответ: Пример 8. Решите неравенство: Решение. Вновь начнем с определения области допустимых значений:
На множестве допустимых значений неравенства проводим равносильные преобразования: После сокращения и перехода к равносильному по теореме 2 неравенству получаем: С учетом области допустимых значений получаем окончательный ответ: Пример 9. Решите логарифмическое неравенство: Решение. Область допустимых значений неравенства определяется следующей системой:
Видно, что в области допустимых значений выражение, стоящее в основании логарифма, всегда больше единицы, а потому равносильным по теореме 2 будет переход к следующему неравенству: С учетом области допустимых значений получаем окончательный ответ: Пример 10. Решите неравенство: Решение. Область допустимых значений неравенства определяется системой неравенств:
I способ. Воспользуемся формулой перехода к новому основанию логарифма и перейдем к равносильному в области допустимых значений неравенству: Неравенство будет равносильно двум системам. Первой: Итак, окончательный ответ: II способ. Решаем методом интервалов. Преобразуем неравенство к виду: Вычтем из знаменателя С учетом того, что выражения Множество решений данного неравенства Итак, Итак, что нужно для того, чтобы решать логарифмические уравнения и неравенства?
Главное же требование — это настойчивость в достижении своей цели. Учитесь, тренируйтесь, если нужно — ежедневно, изучайте и запоминайте на примерах основные способы решения неравенств и их систем, анализируйте возникающие ошибки и не допускайте их в будущем. За помощью в этом нелегком деле вы можете обратиться к своему школьному учителю по математике, репетитору, родителям, друзьям и знакомым, книгам, а также огромному количеству материалов, доступных на просторах Интернета. Желаю вам успехов в подготовке к Единому государственному экзамену по математике. Логарифмические неравенстваРешая логарифмические неравенства, мы пользуемся свойством монотонности логарифмической функции. Также мы используем определение логарифма и основные логарифмические формулы. Давайте повторим, что такое логарифмы: Логарифм положительного числа по основанию — это показатель степени, в которую надо возвести , чтобы получить . Основное логарифмическое тождество: Основные формулы для логарифмов: (Логарифм произведения равен сумме логарифмов) (Логарифм частного равен разности логарифмов) (Формула для логарифма степени) Формула перехода к новому основанию: Алгоритм решения логарифмических неравенств Можно сказать, что логарифмические неравенства решаются по определенному алгоритму. Нам нужно записать область допустимых значений (ОДЗ) неравенства. Привести неравенство к виду Знак здесь может быть любой: Важно, чтобы слева и справа в неравенстве находились логарифмы по одному и тому же основанию. И после этого «отбрасываем» логарифмы! При этом, если основание степени , знак неравенства остается тем же. Если основание такое, что знак неравенства меняется на противоположный. Конечно, мы не просто «отбрасываем» логарифмы. Мы пользуемся свойством монотонности логарифмической функции. Если основание логарифма больше единицы, логарифмическая функция монотонно возрастает, и тогда большему значению х соответствует большее значение выражения . Если основание больше нуля и меньше единицы, логарифмическая функция монотонно убывает. Большему значению аргумента х будет соответствовать меньшее значение Важное замечание: лучше всего записывать решение в виде цепочки равносильных переходов. Перейдем к практике. Как всегда, начнем с самых простых неравенств. 1. Рассмотрим неравенство log3x > log35. Что делать дальше? Стандартный ответ, который дают школьники, — «Отбросить логарифмы!» Что ж, эта формулировка лихо звучит и легко запоминается. Но почему мы все-таки можем это сделать? Мы люди, мы обладаем интеллектом. Наш разум устроен так, что все логичное, понятное, имеющее внутреннюю структуру запоминается и применяется намного лучше, чем случайные и не связанные между собой факты. Вот почему важно не механически вызубрить правила, как дрессированная собачка-математик, а действовать осознанно. Так почему же мы все-таки «отбрасываем логарифмы»? Ответ простой: если основание больше единицы (как в нашем случае), логарифмическая функция монотонно возрастает, значит, большему значению x соответствует большее значение y и из неравенства log3x1 > log3x2 следует, что x1 > x2. Следующее логарифмическое неравенство тоже простое. Начнём с области допустимых значений. Логарифмы определены только для положительных чисел, поэтому Решая эту систему, получим: x > 0. Теперь от логарифмического неравенства перейдем к алгебраическому — «отбросим» логарифмы. Поскольку основание логарифма больше единицы, знак неравенства при этом сохраняется. А что же будет, если основание логарифма меньше единицы? Легко догадаться, что в этом случае при переходе к алгебраическому неравенству знак неравенства будет меняться. 3. Запишем ОДЗ. Выражения, от которых берутся логарифмы, должны быть положительно, то есть Решая эту систему, получим: x > 4,5. Поскольку Получим, что x ≤ 9. Учитывая, что x > 4,5, запишем ответ: В следующей задаче показательное неравенство сводится к квадратному. Так что тему «квадратные неравенства» рекомендуем повторить. Теперь более сложные неравенства: 4. Решите неравенство 5. Решите неравенство Если , то . Нам повезло! Мы знаем, что основание логарифма больше единицы для всех значений х, входящих в ОДЗ. Обратите внимание, что сначала мы полностью решаем неравенство относительно новой переменной t. И только после этого возвращаемся к переменной x. Запомните это и не ошибайтесь на экзамене! 6. Запомним правило: если в уравнении или неравенстве присутствуют корни, дроби или логарифмы — решение надо начинать с области допустимых значений. Поскольку основание логарифма должно быть положительно и не равно единице, получим систему условий: Упростим эту систему: Это область допустимых значений неравенства. Мы видим, что переменная содержится в основании логарифма. Перейдем к постоянному основанию. Напомним, что
Вернемся к переменной x:
Ответ: 7. Следующая задача тоже решается с помощью метода интервалов
0″ src=»https://latex.codecogs.com/png.latex?%5Cfrac%3C2-3x%3E%3Cx%3E%3E0″ />Это условие обязательно должно выполняться, и к нему мы вернемся. Рассмотрим пока само неравенство. Запишем левую часть как логарифм по основанию 3:
Получилось? Что же, повышаем уровень сложности: 8. Решите неравенство: Неравенство равносильно системе: 9. Решите неравенство: Выражение 5 — x 2 навязчиво повторяется в условии задачи. А это значит, что можно сделать замену: Поскольку показательная функция принимает только положительные значения, t > 0. Тогда
Неравенство примет вид: Уже лучше. Найдем область допустимых значений неравенства. Мы уже сказали, что t > 0. Кроме того, ( t − 3) (5 9 · t − 1) > 0 Если это условие выполнено, то и частное А еще выражение под логарифмом в правой части неравенства должно быть положительно, то есть (625 t − 2) 2 . Это означает, что 625 t − 2 ≠ 0, то есть Аккуратно запишем ОДЗ и решим получившуюся систему, применяя метод интервалов.
Ну что ж, полдела сделано — разобрались с ОДЗ. Решаем само неравенство. Сумму логарифмов в левой части представим как логарифм произведения: «Отбросим» логарифмы. Знак неравенства сохраняется. Перенесем все в левую часть и разложим по известной формуле разности квадратов: 0;» src=»https://latex.codecogs.com/png.latex?(t-3)%5E%3C2%3E-(625t-2)%5E%3C2%3E%3E0;» />
Вернемся к переменной x Поскольку
10. Еще один прием, упрощающий решение логарифмических неравенств, — переход к постоянному основанию. Покажем, как использовать переход к другому основанию и обобщенный метод интервалов.
Выражение lg | x − 3| равно нулю, если | x − 3| = 1, то есть x = 4 или x = 2. Выражение lg (| x| − 2) равно нулю, если | x| = 3, то есть в точках 3 и −3. Отметим эти точки на числовой прямой, с учетом ОДЗ неравенства.
Ответ: 11. А в следующей задаче спрятаны целых две ловушки для невнимательных абитуриентов.
0\\ x+2\neq 1\\ 36+16x-x^<2>>0\\ x\neq 18 \end Обратите внимание, что Это пригодится вам при решении неравенства. Упростим исходное неравенство: Теперь главное – не спешить. Мы уже говорили, что задача непростая – в ней расставлены ловушки. В первую вы попадете, если напишете, что
Выражение в левой части этого неравенства не может быть отрицательным, поэтому t = 2. Тогда Мы рассмотрели основные приемы решения логарифмических неравенств — от простейших до сложных, которые решаются с помощью обобщенного метода интервалов. Однако есть еще один интересный метод, помогающий справиться и показательными, и с логарифмическими, и с многими другими видами неравенств. Это метод рационализации (замены множителя). О нем — в следующей статье. Логарифмические уравнения и неравенства.Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах. “ Логарифмические уравнения и неравенства” Различные определения понятия уравнений и неравенств в математике и в школьном курсе математики. Содержательный и формальный подход к определению понятия равенства. Пусть один из элементов некоторого множества М обозначен буквой а, которая не соответствует никакому другому элементу из множества М. Если а считать именем (названием) элемента, то можно просто говорить: элемент а. Может оказаться что тот же самый элемент будет назван другим именем скажем b , причем обозначение b тоже не соответствует никакому другому элементу из М. Если определенно установлено, что a и b обозначают один и тот же элемент, то говорят, что элементы a и b совпадают или они тождественны. Тождественные элементы часто называют равными, для обозначения отношения равенства применяют знак =, а само отношение a = b называют равенством. В математике часто исходят из более общей, формальной трактовки понятия равенства: два аналитических выражения f и g , соединенные знаком = , образуют равенство f = g . Эти определения понятия равенства противоречивы, что послужило источником споров, особенно проявившихся в дискуссиях по поводу трактовки понятия уравнения. Одни участники дискуссий считали, что если выражения U и V не находятся в отношении равенства, то отношение U = V надо называть неверным равенством; другие считали такую точку зрения нелепой: неверных равенств не может быть. Возникающие здесь недоразумения можно устранить, рассматривая вопрос с позиций математической логики. Если U и V – числовые выражения, то соотношение U = V рассматривается как символическая запись высказывания: значения выражения U равно значению выражения V . Но высказывание может быть либо истинным, либо ложным. Если высказывание U = V оказывается ложным, то соотношение U = V называют неверным равенством. Если выражение U или V содержат переменную, то соотношение U = V уже не будет высказыванием – в этом случае его называют высказывательной формой (иногда предикатом) и мы не можем говорить о его истинности до тех пор пока на место переменных в выражениях U и V не будут подставлены их значения. Одно из применений знака равенства в указанном смысле находит место в символической записи уравнения. Определение понятия уравнения. Можно заметить, что в различных определениях понятия уравнения – в некоторых явно в некоторых в более скрытой форме – оно трактуется как символическая запись задачи о разыскании таких систем значений аргументов х1, x 2… xn функций f ( x 1, x 2… xn ) и g ( x 1, x 2… xn ), при которых значения функций f и g равны. При такой трактовке понятия уравнения отчетливо заметна независимость понятий уравнения и тождества и неправомерность рассмотрения тождества как частного случая уравнения. Определение отдельных видов уравнений ( неравенств) – линейных, квадратных, вообще n -ой степени, рациональных, иррациональных, простейших тригонометрических, показательных, логарифмических – вводятся в связи с изучением соответствующих функций. Кстати, остановимся на вопросе о классификации уравнений и неравенств. Уравнения (неравенства) классифицируются по виду функций, представляющих левую и правую части уравнений (неравенств). Уравнение f ( x )= g ( x ) называется: алгебраическим, если f ( x ) и g ( x ) – алгебраические функции трансцендентными, если хотя бы одна из функций f ( x ) и g ( x ) трансцендентная рациональным алгебраическим, если алгебраические функции f ( x ) и g ( x ) рациональные иррациональным алгебраическим, если хотя бы одна из алгебраических функций f ( x ) и g ( x ) иррациональная целым рациональным, если функции f ( x ) и g ( x ) целые рациональные дробным рациональным, если хотя бы одна из рациональных функций f ( x ) и g ( x ) дробная рациональная Уравнение P ( x ) =0, где P ( x ) — многочлен стандартного вида, называется линейным (первой степени) квадратным ( второй степени) кубичным (третьей степени) четвертой степени и вообще n -ой степени если многочлен P ( x ) имеет соответственно первую вторую третью четвертую и вообще n -степень. Таким образом, понятие степени уравнения (неравенства) определено лишь для уравнений ( неравенств) указанного вида, поэтому нет смысла ставить вопрос, какую степень относительно переменной имеют уравнения другого вида. Отчетливое понимание существа понятий равенства, тождества и уравнения и знание различных вариантов соответствующих определений необходимы для учителя. Но следует иметь в виду, что в школьном курсе математики соответствующие определения не включаются в логические операции, поэтому нет необходимости требовать от учащихся запоминания этих определений. Говоря несколько прямолинейно надо не столько уметь определять, что такое уравнение, сколько научится их решать. Определение понятия неравенства. Если элементы а и b некоторого множества не находятся в отношении неравенства. Это отношение выражается записью: а неравно b . В некоторых множествах один из двух неравных элементов может находится в особом отношении с другим – в отношении предшествования. В зависимости от природы элементов множества в понятие предшествования может вкладываться различный конкретный смысл. Например, на множестве людей отношение предшествования может быть установлено следующим способом: будем говорить, что человек А предшествует человеку В, если А ниже (по росту) В. Другой интерпретацией предшествования на множестве людей может служить отношение моложе. На множестве действительных чисел отношение предшествования обычно называют отношением меньше. Оставляя в стороне вопрос о развитии понятия меньше, в связи с развитием понятия числа от натурального до действительного, введем следующее определение: если разность а- b действительных чисел а и b отрицательна, то говорят, что число а меньше числа b , и пишут a b . Если а b , то говорят, что b больше а, что выражают записью: b > a . На множестве действительных чисел рассматриваются также отношения не больше и не меньше: если a — b – число отрицательное или равно 0 ( т. е. не положительное), то говорят, что а не больше b . Все отношения имеют общее название неравенств. На множестве F функций от аргументов x 1, x 2… xn , с общей областью определения функций D отношение меньше устанавливается следующим образом. Говорят что функция F 1 принадлежит F находится в отношении меньше с функцией F 2 принадлежащей F над множеством D если при каждой системе значений аргументов ( x 1, x 2… xn ) принадлежащих D значение функций F 1 меньше значений функций F 2. Наличие отношения меньше функции F 1 с функцией F 2 над множеством D передается записью F 1 F 2. Это неравенство называется также тождественным неравенством над множеством D . Для понятия неравенства существует формальная характеристика: два аналитических выражения U и V соединенные знаком U V . Соответствующий знак неравенства выражает наличие высказывания или предиката о неравенстве U и V в зависимости от того являются ли U и V числовым выражением или выражениями с переменными. В учении о неравенствах аналогом понятия уравнения является понятие неравенства с переменными (неизвестными). Оно может быть определено следующим образом: пусть даны две функции F 1( x 1, x 2… xn ) и F 2 ( x 1, x 2… xn ). Символическая запись задачи о разыскании таких систем значений аргументов (х1, x 2… xn ) при которых значение функции F 1 находится в отношении ^ со значением функции F 2 называется неравенством с переменными x 1, x 2… xn . Символически неравенство с переменными записывается как обычное неравенство F 1 ( x 1, x 2… xn )^ F 2( x 1, x 2… xn ). Вэтой формуле знак выступает не в роли знака истинного отношения неравенства функции F 1 с функцией F 2 а в роли знака указывающего на отношение неравенства значения функции F 1 со значением функции F 2 предиката отвечающего постановке указанной задачи. На понятие суждения опирается и определение неравенства с неизвестными приведенное в специальном курсе элементарной алгебры С. И. Новоселова (1962, с. 230): Неравенство F 1 ( x , y … z ) F 2( x , y … z ), выражающее следующее суждение: значение функции F 1 меньше значения функции F 2 называется неравенством с неизвестными x y z . Когда-то в вузовских пособиях по элементарной математике такие неравенства было принято называть условными неравенствами. Не обсуждая вопроса о том насколько удачными являются названия неравенство с переменными или неравенство с переменными условное неравенство отметим что с методической точки зрения необходимо отчетливо выделить понятие роль которого в учении о неравенствах аналогична роли понятия уравнения в учении о равенствах, т.е. приписать этому понятию определенное название. Без этого возникает много неудобств и недоразумений, особенно при изучении неравенств в школе. Однако с той же точки зрения очевидно что вводя новый термин мы должны построить соответствующее определение аналогично построению определения уравнения. Но это оказывается крайне неудобным хотя бы с лингвистической точки зрения. Например, если в учебнике сказано что равенство с переменной называют уравнением то аналогичное определение должно звучать тавтологически (неравенство с переменной называют…). Естественно что в этом учебнике вообще дается определения новому понятию, а оно вводится на основе решения конкретной задачи. Мы предпочитаем пользоваться названием неравенства с переменными которое подчеркивает назначение понятия обозначаемого этим термином – выражать постановку задачи о которой уже говорилось. Там где это не приводит к недоразумениям вместо неравенства с переменными говорят короче неравенство. Общую часть областей определения функций F 1 и F 2 представляющих левую и правую части неравенства F 1^ F 2 называют областью определения неравенства или областью (множеством) допустимых систем значений переменных (ОДЗ). Всякая допустимая система значений неизвестных, при которой неравенство F 1^ F 2 верно называется решением неравенства. Решить неравенство – значит найти все множество его решений. Зачем в школе изучают логарифмы Вопрос о мотивации обучения по-прежнему остается первостепенным при организации учебного процесса, ведь интерес к учебе – это и есть необходимая почва для сотрудничества учащихся и учителя. Логарифмы появились в XVI веке под влиянием все возрастающих потребностей практики как средство для упрощения вычислений. Основная идея логарифмов лежит в сопоставлении арифметической и геометрической прогрессий: 0 1 2 3 4 5 6 7 8 9 … n … 1 2 4 8 16 32 64 128 256 512 …2 n … Эти строки позволяют упрощать вычисления: сводить умножение к сложению, деление к вычитанию, возведение в степень к умножению, извлечения корня к делению. Например, чтобы перемножить числа нижнего ряда 8 и 64, мы складываем соответствующие числа верхнего ряда 3 и 6 (3+6=9), находим в нижнем ряду ответ под цифрой 9. Аналогично объясняются и упрощения других вычислений с числами нижнего ряда с помощью чисел верхнего ряда. Числа верхнего ряда ( показатели степеней) и называются логарифмами чисел нижнего ряда. Однако у учащихся может возникнуть встречный вопрос. Если в XVI веке логарифмы появились как средство для упрощения вычислений то нужны ли они сегодня, когда вычислительная техника достаточно развита чтобы справляться с самыми сложнейшими расчетами? Вопрос правомерен. Ведь не изучаются же в современной школе такие старинные средства для упрощения вычислений как простейшие счетные приборы, не изучаются древние алгоритмы умножения и деления чисел, извлечения квадратных и кубических корней и прочее. Так зачем изучают логарифмы сегодня? Во-первых, на что можно обратить внимание учащихся – это на то, что они только начав изучение данной темы уже умеют записать решение показательного уравнения. Таким образом, значение логарифмов позволит им решать задачи сводящиеся к простейшим показательным уравнениям. Во-вторых, обязательно надо отметить, что логарифмы и сегодня позволяют упрощать вычисления. Представим себе, что нам необходимо найти максимум функции F ( x ) = f 1( x ) f 2( x )… f n ( x ), положительной для любого х. Для этого необходимо найти производную функции. Правило производной произведения двух функций не очень простое, а здесь его надо обобщить на n функций. В этом случае математики часто поступают следующим образом: рассматривают функцию ln F ( x ) = ln f 1( x ) + ln f 2( x ) +…+ ln f n ( x ). Производная суммы находится несложно, а найденное значение х, в котором функция ln F ( x ) достигает максимума также является тем значением, в котором достигает максимума и F ( x ) ( в силу монотонности логарифмической функции). Наконец нами произнесены ключевые слова: логарифмическая функция. Именно ее изучение в конечном итоге является целью рассматриваемого раздела школьной программы и именно эта тема так важна для общего образования учащегося. Испокон веков целью математической науки было помочь людям узнать больше об окружающем мире, познать его закономерности и тайны. Математики выделяя самые существенные черты того или иного наблюдаемого в природе явления вводя числовые характеристики и связывая эмпирические данные с помощью различных математических зависимостей тем самым сопоставляют математическую модель явления. Изучение этой модели позволяет людям больше узнать о природном явлении, глубже уяснить его природу и свойства. Ряд явлений природы помогает описать именно логарифмическая зависимость. Иначе говоря, математики, пытаясь составить математическую модель того или иного явления, достаточно часто обращаются именно к логарифмической функции. Одним из примеров такого обращения является логарифмическая спираль. Уравнение логарифмической спирали в полярной системе координат имеет вид р= a Переписав уравнение в виде Спираль в одну сторону развертывается до бесконечности, а вокруг полюса напротив закручивается стремясь к нему, но не достигая. Так почему же в качестве примера логарифмической зависимости в природе мы выбрали именно логарифмическую спираль? Известно что живые существа обычно растут сохраняя общее начертание свое формы. При этом чаще всего они растут во всех направлениях – взрослое существо и выше и толще детеныша. Но раковины морских животных могут расти лишь в одном направлении. Чтобы не слишком вытягиваться в длину им приходиться скручиваться причем рост совершается так, что сохраняется подобие раковины с ее первоначальной формой (рис.2). А такой рост может совершаться лишь по логарифмической спирали или ее некоторым пространственным аналогам. Поэтому раковины многих моллюсков, улиток, а также таких млекопитающих как архары ( горные козлы) закручены по логарифмической спирали (рис.3). Можно сказать, что эта спираль является математическим символом соотношения формы и роста. Великий немецкий поэт Иоганн-Вольфганг Гете считал ее даже математическим символом жизни и духовного развития. По логарифмической спирали очерчены не только раковины. Один из наиболее распространенных пауков эпейра, сплетая паутину, закручивает нити вокруг центра по логарифмическим спиралям. В подсолнухе (рис.4) семечки расположены по дугам близким к логарифмическим спиралям. По логарифмическим спиралям закручены и многие галактики, в частности, Галактика, которой принадлежит Солнечная система. (рис.5). Логарифмические линии в природе замечают не только математики, но и художники. Например, этот вопрос чрезвычайно волновал Сальвадора Дали. Однажды 18 декабря 1955 года он вынес его на повестку своего публичного выступления, которое проходило в Париже в главной аудитории Сорбонны. Сальвадоро Дали рассказал о том, что происходило в Сорбонне в своем дневнике, из которого мы приведем небольшие отрывки. “ Воспоминания 9-летнего возраста… моей навязчивой идеей настоящей маниакальной страстью стала картина Вермеера Кружевница репродукция которой висела в отцовском кабинете”. “ Уже много лет спустя я попросил в Лувре разрешение написать копию с этой картины. Потом я попросил киномеханика показать на экране репродукцию нарисованной мною копии … Я объяснил, что пока не написал эту копию, в сущности почти ничего не понимал в Кружевнице и мне понадобилось размышлять над этим вопросом целое лето, чтобы осознать наконец, что я инстинктивно провел на холсте строгие логарифмические кривые…”(рис.7). “ Одновременно с этим я углубил свои исследования по морфологии подсолнуха – вопросу, по которому в свое время сделал чрезвычайно интересные выводы еще Леонардо да Винчи. Сейчас морфологи выражают сомнения по поводу того, являются ли спирали подсолнуха действительно логарифмическими спиралями. Конечно, они к ним очень близки, но случаются такие пересечения которые вообще в принципе невозможно измерить со строго научной точностью, так что мнения морфологов насчет того спирали это или не спирали расходятся. В то же время я имел вчера вечером в Сорбонне все основания утверждать перед собравшейся публикой, что никогда еще в природе не существовало столь совершенного примера логарифмических спиралей”. Логарифмическая спираль знаменита не только тем, что ее образы достаточно широко встречаются в природе, но и своими удивительными свойствами. Приведем некоторые из них. На одно из таких свойств мы выходим при попытке построить логарифмическую спираль. Для этого возьмем n точек M ( u , t ). Пусть первые координаты этих точек образуют арифметическую прогрессию с разностью u 0, а тогда вторые координаты – геометрическую прогрессию. Построим луч, составляющий с полярной осью угол u 1 – первая координата первой выбранной нами точки и будем поворачивать все время этот луч на угол u 0 до тех пор, пока не достигнем значения первой координаты последней n -й из выбранных точек. (рис. 8). Далее на лучах отметим нужные точки M . Если для наглядности все отрезки OM i = a ui отложить на одном луче (рис. 9), то будет очевидно, что каждая точка Mi переходит в точку M i +1 при гомотетии с коэффициентом к= a u 0 Теперь рассмотрим преобразование g = h Пусть … M -2, M -1, M 0, M 1, M 2 … — последовательность точек, переходящих друг в друга при преобразовании g , т.е. для любого целого i верно, что g ( M i )= M i +1. Тогда в силу рассмотренных выше рассуждений эти точки лежат на одной логарифмической спирали. Рассмотренное преобразование g = h Логарифмическая спираль остается неизменной не только при преобразовании подобия, но и при других преобразованиях. Это свойство поразило впервые изучавшего ее Якоба Бернулли, что он был склонен придать им мистический смысл и пожелал иметь на своей могильной плите изображение логарифмической спирали (называл он ее дивной спиралью) с надписью: измененная, воскресаю прежней. Неизменяемость спирали при преобразовании подобия является основой любопытного явления состоящего в том, что если лист бумаги с изображенной на нем логарифмической спиралью быстро поворачивать вокруг полюса по ходу часовой стрелки или против, то можно наблюдать кажущееся увеличение или уменьшение спирали. Рассмотрим еще одно важное свойство, связанное с касательной. Определим угол v 0 составляемый касательной в произвольной точке логарифмической спирали с радиус – вектором точки касания по формуле tg v = Для логарифмической спирали tg v = Этот угол зависит лишь от параметра а и, следовательно, для каждой спирали является постоянным. Иными словами, логарифмическая спираль пересекает свои радиус-векторы под постоянным углом. На основании этого логарифмическую спираль называют также равноугольной. Из всех кривых подобным свойством обладает, кроме логарифмической спирали, окружность, которая пересекает свои радиусы под прямым углом. Но и окружность можно рассматривать как частный вид спирали ибо полагая а=1, получаем из уравнения спирали р= a u уравнение окружности р =1. Последнее свойство логарифмической спирали находит в частности применение в технике. Дело в том что в технике часто применяются вращающиеся ножи (рис. 10). Сила с которой они давят на разрезаемый материал зависит от угла резания, т.е. угла между лезвием ножа и направлением скорости вращения. Для постоянного давления нужно чтобы угол резания сохранял постоянное значение, а это будет в том случае, если лезвия ножей очерчены по дуге логарифмической спирали. Величина угла резания зависит от отрабатываемого материала. Логарифмическая спираль – это замечательная кривая, имеющая очень много интересных свойств, но примеры логарифмической функции в природе на этом не ограничиваются. Поэтому рассмотрим еще несколько интересных фактов. Известно, что астрономы распределяют звезды по степеням видимой яркости на светила первой величины, второй величины, третьей и т. д. Последовательные звездные величины воспринимаются глазом как члены арифметической прогрессии. Но физическая яркость их изменяется по иному закону: объективные яркости составляют геометрическую прогрессию со знаменателем 2,5. Получается, что величина звезды представляет собой не что иное как логарифм ее физической яркости. Таким образом, оценивая видимую яркость звезд, астроном оперирует с таблицей логарифмов по основанию 2,5. Практически аналогичная картина получается при оценивании громкости шума. Единицей громкости служит бел ( в честь изобретателя телефона А.Г. Белла), практически – его десятая доля, децибел. Последовательные степени громкости 10 децибел 20 децибел и т.д. составляют для нашего слуха арифметическую прогрессию. Физическая же сила этих шумов ( точнее-энергия) составляет геометрическую прогрессию со знаменателем 10. Громкость шума выраженная в белах равна десятичному логарифму его физической силы. Рассмотрим этот вопрос подробнее. Сила звука – это количество звуковой энергии, проходящей через единицу поверхности в единицу времени. Установлено, что эта величина не выражает величины нашего звукового ощущения – громкости. Если мы будем слушать звуки различных частот но одинаковой силы то они покажутся нам отличающимися по громкости. То есть наше ухо с разной чувствительностью воспринимает звуки различной частоты. Если увеличивать силу какого-нибудь звука в 2, 3, 4 раза, то наше звуковое ощущение (громкость звука) во столько же раз не увеличивается. Тихий шелест листьев оценивается в 1 бел, громкая разговорная речь – в 6,5 бела, рычание льва – в 8,7 бела. Но разности громкостей в 1 бел отвечает отношение силы шумов равное 10. По силе звука разговорная речь превышает шелест листьев в 10 6,5-1 = 10 5,5 =316000 раз; львиное рычание сильней громкой разговорной речи в 10 8,7-6,5 =10 2,2 =158 раз. При оценке видимой яркости светил и при измерении громкости шума мы имеем дело с логарифмической зависимостью между величиной ощущения и порождающего его раздражения. Оказывается, что оба эти явления – следствие общего психофизического закона Вебера-Фехнера, согласно которому ощущение изменяется пропорционально логарифму раздражения. Как видно, логарифмы вторгаются и в область психологии. Учащиеся, обучаясь в школе не просто впитывают некоторый набор информации. Они усваивают научные данные об окружающем мире об его устройстве и законах. Именно в этот период у них складывается картина мира и чем полнее объективнее она будет тем лучше они будут понимать и оценивать окружающую их жизнь тем более полноценным человеком будут себя ощущать. Поэтому в программу общеобразовательной школы входят вопросы, без которых картина мира учащегося будет неполноценной. Учителя математики должны особенно помнить об этом, ведь часто увлекаясь математической стороной вопроса, мы забываем раскрыть его гуманитарную ауру. А это приводит, с одной стороны, к отсутствию личной заинтересованности учащихся в успешности своих занятий математикой в школе, а с другой стороны, к неверному пониманию роли математики в системе человеческого знания. Если первая беда застигает в основном слабых учащихся, то от второй не застрахован даже сильный ученик. В школьных курсах алгебры тема “Логарифмы и логарифмическая функция” изложена недостаточно четко и полно. Приведем несколько примеров. При переходе от уравнения При решении уравнения вида a f ( x ) = a h ( x ) используется свойство: при одном и том же основании равные числа имеют равные логарифмы. На эти свойства в учебниках алгебры внимание учащихся не акцентируется. Недостаточно четко и полно излагаются и свойства логарифмической функции. Логарифмирование производится путем подсчета, сколько раз основание входит множителем в данное выражение или, другими словами, с каким показателем степени надо взять основание, чтобы получить данное число, а результат такого подсчета называется логарифмом определяемого числа при данном основании. Найти логарифм число N при основании а значит ответить на вопрос из скольких сомножителей равных а составляется число N . Логарифм N при основании а есть тот показатель степени, который надо снабдить основание а, чтобы получить число N . Логарифм N при основании а обозначаются знаком log a N . Запись log a N = m равносильна, утверждению, что N = a m . Преподавание алгебры в школах основывается на базе функциональной зависимости величин, а поэтому и теория логарифмов строится на той же базе. Все действия с показателями объединяются в одну главу и рассматриваются в связи с показательной функцией. Логарифмическая функция (как обратная показательной) изучается после показательной. Такой метод изложения теории является наиболее рациональным, так как понятие о функции доминирует в современной математике и должно играть руководящую роль в курсе алгебры средней школы, в частности при изучении логарифмов. Подобное изложение теории логарифмов содержат очень многие современные элементарные учебники по алгебре. В учебной и методической литературе существует три приема изложения теории логарифмов и логарифмической функции. 1. Рассматриваются две прогрессии: арифметическая и геометрическая. Сопоставление этих двух прогрессий приводит к выводу: умножение, деление, возведение в степень членов геометрической прогрессии можно заменить сложением, вычитанием, умножением членов арифметической прогрессии. Затем вводится понятие логарифма, а далее рассматриваются логарифмы при любом основании и применение логарифмов при вычислениях. Только после этого изучается логарифмическая функция. 2. Вначале дается определение логарифма как показателя степени, а затем рассматриваются логарифмическая функция и применение логарифмов при вычислениях. 3. Прежде всего дается понятие логарифмической функции как функции, обратной по отношению к показательной, рассматриваются их свойства, затем вводится определение логарифма, говорится и о применении логарифмов к вычислениям. По сложившейся традиции логарифмическая функция в средней школе определяется как обратная показательной. При таком методе изложения показательная функция является основой построения теории логарифмов. Формулы, свойства, применяемые в школьном курсе математики при изучении логарифмов, логарифмических уравнений и неравенств. В школьных курсах алгебры тема “Логарифмы и логарифмическая функция” изложена недостаточно четко и полно: в учебниках отсутствует теоретический материал, необходимый для обоснования решения некоторых видов логарифмических уравнений, примеров на свойства логарифмов, неравенств, содержащих логарифмы и т.д. Приведем несколько примеров. При переходе от уравнения При решении уравнения вида a f ( x ) = a h ( x ) используется свойство: при одном и том же основании равные числа имеют равные логарифмы. На эти свойства в учебниках алгебры внимание учащихся не акцентируется. Недостаточно четко и полно излагаются и свойства логарифмической функции. Логарифмирование производится путем подсчета, сколько раз основание входит множителем в данное выражение или, другими словами, с каким показателем степени надо взять основание, чтобы получить данное число, а результат такого подсчета называется логарифмом определяемого числа при данном основании. Найти логарифм число N при основании а значит ответить на вопрос из скольких сомножителей равных а составляется число N . Логарифм N при основании а есть тот показатель степени который надо снабдить основание а чтобы получить число N . Логарифм N при основании а обозначаются знаком log a N . Запись log a N = m равносильна, утверждению, что N = a m . Свойство 1. При положительном основании отрицательные числа и нуль не имеют логарифмов. Дано: log a N не существует. Доказательство: Предположим что log a N , где N k т.е. log a N = k . Тогда по определению логарифма a k = N . Но a k >0 (при положительном основании функция у=а х — положительна), а N Таким образом, пришли к противоречию: положительное число (а к ) равно отрицательному числу или нулю ( N ). Следовательно отрицательные числа и нуль при положительном основании не имеют логарифмов. Свойство 2. При положительном основании каждое положительное число имеет логарифм. Доказать: lg a N – действительное число. Доказательство этого свойства мы опустим из-за его сложности, а покажем на частном примере нахождение логарифма некоторого положительного числа по какому-либо основанию с любой степенью точности. Пусть требуется например lg 2 с точностью до 0,1. Положим lg 2 = x /10. Отсюда ( по определению логарифма) 10 x /10 = 2 или возвысив обе части последнего равенства в 10-ю степень получим: 10 x =2 10 или 10 x = 1024 Значит, lg 2 = x /10 Для нахождения log 2 с точностью до 0,01 положим lg 2 = x /100. Сделав аналогичные преобразования получим: 10 x /100 =2,10 x =2 100 =(2 10 ) 10 =1024 10 10 x Замечание. Применяя указанный способ и рассмотренные ниже свойства логарифмов можно было бы составить таблицы логарифмов чисел по любому положительному основанию с любой степенью точности но указанный способ очень сложный. Математика дает более простые способы вычисления которые выходят за рамки школьной программы. Свойство 3. Числа имеющие при одном и том же основании равные логарифмы равны между собой. Доказательство. Обозначив log a N 1= log a N 2 через к по определению логарифма получим: N 1= a k и N 2= a k , откуда N 1= N 2. (Две величины порознь равные третьей равны между собой.) Свойство 4. При одном и том же основании равные числа имеют равные логарифмы. Доказательство. Положив log a N 1= k , a log a N 2= m (1) рассмотрим относительно основания а два случая: 1) а>1 Случай 1. (а>1). Из (1) по определению логарифма имеем: a k = N 1 и a m = N 2, откуда a k = a m , или a k — a m =0, a k (1- a m — k )=0. Но a k Последнее равенство возможно при m — k =0, т.е. при m = k . В самом деле если m — k >0, то a m — k >1, а если m — k a m — k 1). Случай 2 доказывается аналогично. Итак доказано что m = k , т. е. log a N 1= log a N 2. Замечание. Так как логарифм есть показатель степени то это свойство можно сформулировать и так: если степени равны основания степеней равны то и показатели степеней равны. Из свойств 2 и 4 заключаем: Каждое положительное число имеет единственный логарифм. Теоремы о логарифмах. Доказательства и формулировки теорем о логарифме произведения, частного, степени и корня общеизвестны, а потому я на них не останавливаемся. Однако я считаю целесообразным доказать справедливость теоремы о логарифмировании произведения произвольного числа n сомножителей, применяя метод математической индукции. Будем считать доказанным равенство: Докажем справедливость равенства: 1. Теорема справедлива для произведения двух сомножителей: 2. Предположим, что теорема справедлива и для произведения произвольного числа k сомножителей, т.е. что Докажем что эта теорема будет справедлива и для произведения k +1 сомножителя, т.е. справедливо равенство: Но по предположению Следовательно, окончательно имеем: что и требовалось доказать. Основное логарифмическое тождество. Это тождество вытекает из определения логарифма. В самом деле, положив log a N = k , получим a k = N , но k = log a N , а поэтому a log a N = N . Пользуясь этим тождеством, можно доказать теоремы о логарифмах, как это сделано, например, в учебнике алгебры А.Н. Барсукова. Модуль перехода от одной системы логарифмов к другой. Существуют различные системы логарифмов. Основными являются десятичные (основание 10) и натуральные (основание – иррациональное число е=2,718231…). Покажем, как, зная логарифм некоторого числа по основанию, например а, найти логарифм того же числа по основанию b . Итак, пусть log a N = k . Найдем log a N . log a N = k , отсюда b k = N . Прологарифмировав обе части полученного равенства по основанию а, получим: klog a b = log a N , откуда Поясним на примере, как с помощью этой формулы, зная логарифм числа по одному основанию, найти логарифм того же числа по другому основанию. Например, пользуясь десятичными таблицами логарифмов, найдем log 28. Таким образом, с помощью этой формулы, пользуясь таблицей десятичных логарифмов чисел, мы можем найти логарифм любого положительного числа по другому положительному основанию. Примем модуль перехода к доказательству следующего свойства логарифмов. Свойство 5. Величина логарифма не изменится, если основание логарифмов и число, стоящее под знаком логарифма, возвысим в одну и ту же степень (или извлечем корень одной и той же степени), т.е. log a N = log a n N n Доказательство: Воспользуемся модулем перехода для преобразования log a N n к логарифму с основанием а. Здесь log a a n = n – по определению логарифма. log a N n = nlog a N — по теореме о логарифме степени. Логарифмические и показательные уравнения и неравенства. Логарифмические и показательные уравнения.
a>0 a logaU=logaV a Равносильность следует из строгой монотонности как показательной (в(1)), так и логарифмической (в(2)) функций. З a Выбор зависит от того, какое из неравенств, U >0 или V >0, вам проще решить. a >0 a Рассмотрим несколько примеров решения показательных и логарифмических уравнений, с которыми вы встречаетесь на уроках алгебры и начал анализа. Пример 1. 3 х-3 =7 Решение. По определению логарифма имеем: 3 х-3 =7 О и log 3189 Пример 2. 2 2х-1 =3 2х-1 Решение. Т.к. 3 2х-1 2 2х-1 =3 2х-1 Поскольку 1=(2/3) 0 , последнее уравнение равносильно такому: 2 x -1=0 О 1/2 Можно было решать это уравнение, логарифмируя обе его части, то есть пользуясь равносильным переходом (2). Покажем этот способ решения на следующем примере. Пример 3. 3 х+1 =5 х-2 Решение. Воспользуемся равносильным переходом (2): логарифмическая функция строго монотонна, поэтому каждое свое значение она принимает ровно один раз. 3 х+1 =5 х-2 О Замечание. С таким же успехом как по основанию 10 можно было логарифмировать данное уравнение и по любому другому основанию. Несколько компактнее была бы запись при логарифмировании по основанию 3 или 5 – эти основания уже имеются в условии задачи. Теперь рассмотрим примеры в которых равносильный переход (2) набирает силу. Пример 4. log 5( x -2)=1 Решение. log 5( x -2)=1 Решение. log 7 log 3 log 2 x =0 Пример 6. log 2( x 2 -3 x +1)= log 2(2 x -3) Р 2 x -3>0
x >3/2 П Решение. lg x + lg ( x +3) =1
Поясним равносильность первого перехода. Здесь мы воспользовались формулой log a U + log a V = log a ( UV ), левая часть которой имеет смысл, когда U >0 и V >0, а правая часть – когда UV >0. Поэтому при использовании этой формулы слева направо расширяется область определения уравнения и для равносильности надо ввести дополнительное условие З logaU+logaV=c Решение. Воспользуемся тождеством log a b 2 = 2 log 2 log 2 При следующем переходе мы опускаем условия x +2>0 и x И x 2 +2 x -1=0 x = -1
x 2 +2 x +1=0 ( x +1) 2 =0 x =-1 Ответ: -1; Скажем несколько слов по поводу уравнений в которых встречается степенно-показательная функция y =( f ( x )) g ( x ) . Мы будем считать, что эта функция определена если f ( x )>0; таким образом если в уравнении или неравенстве встретилось выражение ( f ( x )) g ( x ) , то неравенство f ( x )>0 является одним из условий определяющих ОДЗ (область допустимых значений) Возможны и другие определения. Единой общепринятой договоренности в этом нет. Если вам встретилась задача с такой функцией надо обязательно четко указать какого определения вы придерживаетесь. Так в нашем определении значения х=0 и х=-1 не являются корнями уравнения x = x x +2 так как эти значения не входят в область определения функции y = x x +2 .
f g ( x ), h ( x ) определены Логарифмические и показательные неравенства. И следует равносильность таких переходов: a>1 a l a>1 Р Log 0,5 (x+1)>log 0,5 (2-x) Пример 2. (1/3) 2 x Решение. Заменив в правой части 2 на (1/3) log 1/3 2 и прологарифмировав неравенство по основанию 1/3 приходим к неравенству 2 x > log 1/32. Ответ: (1/2 log 1/32; Пример 3. log x 2 Р (3x+1) 2 >x 2 или 0 2 2 8 x 2 +6 x +1>0 или x
Ответ: (-1; -1/2)
f f
f(x) q(x) >f(x) h(x) q ( x ), h ( x ) определены. Он отличается от перехода (11) тем что случай f ( x ) =1 рассматривается отдельно, но при решении задач последний переход очевидно требует лишних вычислений. Однако иногда полезно применять его для самопроверки. l
log f(x) q(x)>log f(x) h(x) “ … Сейчас как никогда становится ясным что математика – это не только совокупность фактов изложенных в виде теорем но прежде всего – арсенал методов и даже еще прежде того – язык для описания фактов и методов самых разных областей науки и практической деятельности.” (Успенский В.) Математика как всякая другая наука находится в непрерывном развитии обусловленным двумя основными причинами: потребностями жизненной практики и внутренними потребностями становления самой математики. Бурное развитие математики оказывает большое внимание на развитие техники, экономики, управление производством, на другие науки, в том числе, на педагогику и методику математики. Практические цели стоящие перед математиками привели к серьезному расширению арсенала вычислительных средств и приемов численного решения задач. Главными достижениями в этом плане являлись : изобретение логарифмов и методов точного или приближенного вычисления корней алгебраических уравнений. Все эти нововведения обогатили элементарную математику. В то же время каждое из этих открытий несло в себе элементы получившие развитие в неэлементарных ее частях в математическом анализе и в высшей алгебре. В этом проявилась особенность неразделимого массового развития всего состава математики и относительность искусственность ее деления на элементарную и высшую на различные дисциплины и т. д. Не надо никогда забывать что выделение одной из сторон математики хотя и облегчает ее изучение но обедняет омертвляет огрубляет общую картину развития всей совокупности математических знаний. Вопрос о связях и взаимодействиях как внутри так и нематематических – остается коренным вопросом всей математики особенно в случаях когда речь идет о ее логарифмической структуре или о путях ее развития об ее истории. Логарифмы служат одним из бесчисленных подтверждений мысли о взаимоотношении теории и практики блестяще выраженное великим русским математиком П.Л.Чебышевым: ” Практика предлагает вопросы существенно новые для науки и таким образом вызывает на изыскание совершенно новый метод. Если теория требует много от новых приложении старой методы или от новых развитие ее то она еще больше приобретает открытием новый метод и в этом случае науки находят себе верного руководителя в практике”. источники: http://ege-study.ru/logarifmicheskie-neravenstva-1/ http://infourok.ru/logarifmicheskie-uravneniya-i-neravenstva-983355.html |
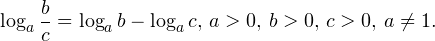 0,\, b>0,\, c>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>
0,\, b>0,\, c>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>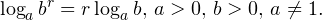 0,\, b>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>
0,\, b>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>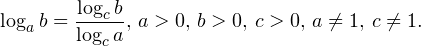 0,\, b>0,\, c>0,\, a\ne 1,\, c\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>
0,\, b>0,\, c>0,\, a\ne 1,\, c\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>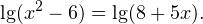
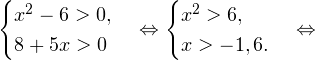 0, \\ 8+5x > 0 \end
0, \\ 8+5x > 0 \end 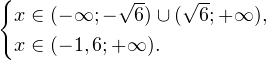
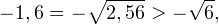 -\sqrt<6>, \]» title=»Rendered by QuickLaTeX.com»/>
-\sqrt<6>, \]» title=»Rendered by QuickLaTeX.com»/>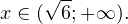
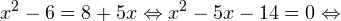
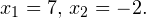
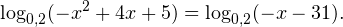
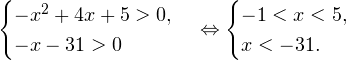 0, \\ -x-31>0 \end
0, \\ -x-31>0 \end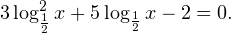
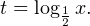
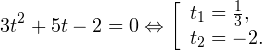
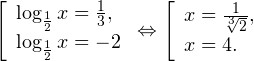
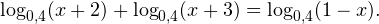
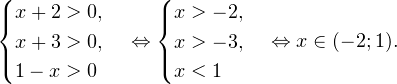 0, \\ x+3>0, \\ 1-x>0 \end
0, \\ x+3>0, \\ 1-x>0 \end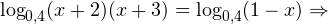
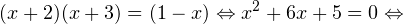
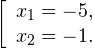
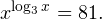
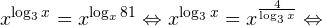
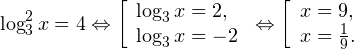
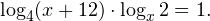
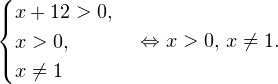 0, \\ x>0, \\ x\ne 1 \end
0, \\ x>0, \\ x\ne 1 \end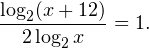
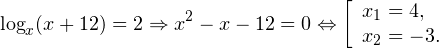
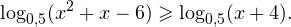
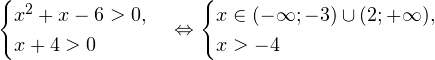 0, \\ x+4>0 \end
0, \\ x+4>0 \end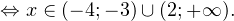
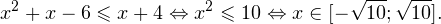
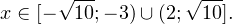
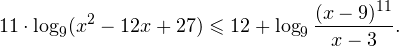
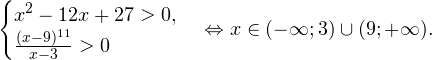 0, \\ \frac<(x-9)^<11>>
0, \\ \frac<(x-9)^<11>>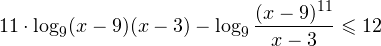
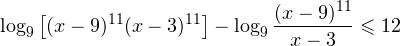
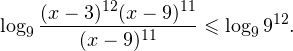
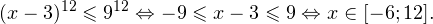
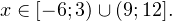
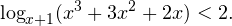
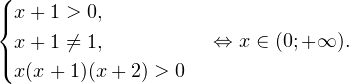 0, \\ x+1\ne 1,\\ x(x+1)(x+2)>0 \end
0, \\ x+1\ne 1,\\ x(x+1)(x+2)>0 \end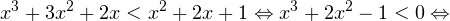
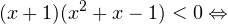
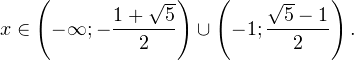
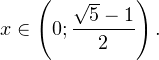
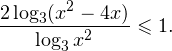
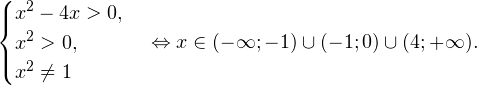 0, \\ x^2>0, \\ x^2\ne 1 \end
0, \\ x^2>0, \\ x^2\ne 1 \end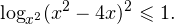
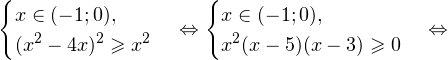
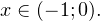
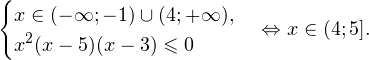
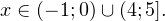
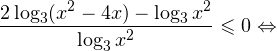
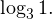 Это ничего не изменит, поскольку
Это ничего не изменит, поскольку 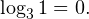
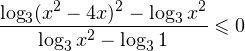
 и
и  — одного знака при
— одного знака при 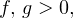 0,» title=»Rendered by QuickLaTeX.com» height=»18″ width=»74″ style=»vertical-align: -4px;»/> в области допустимых значений имеет место следующий равносильный переход:
0,» title=»Rendered by QuickLaTeX.com» height=»18″ width=»74″ style=»vertical-align: -4px;»/> в области допустимых значений имеет место следующий равносильный переход: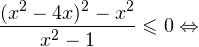
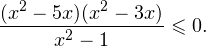
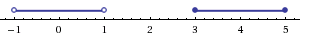
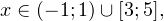 а с учетом области допустимых значений получаем тот же результат:
а с учетом области допустимых значений получаем тот же результат: 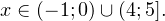






 Ответ:
Ответ:  Итак,
Итак, 
 Вспомним, что
Вспомним, что  Получим, что
Получим, что  Ответ:
Ответ:  Воспользуемся формулой
Воспользуемся формулой  Найдем знак функции g(x) на каждом из промежутков, на которые эти точки разбивают область допустимых значений. Точно так же мы решали методом интервалов обычные рациональные неравенства.
Найдем знак функции g(x) на каждом из промежутков, на которые эти точки разбивают область допустимых значений. Точно так же мы решали методом интервалов обычные рациональные неравенства.

 , где a >0 (рис. 1).
, где a >0 (рис. 1). = log a р мы видим, что величина полярного угла пропорциональна логарифму радиус-вектора. Отсюда и происходит название логарифмическая спираль.
= log a р мы видим, что величина полярного угла пропорциональна логарифму радиус-вектора. Отсюда и происходит название логарифмическая спираль.



 r , где r – поворот вокруг точки O на угол u 0 , а h – гомотетия с центром О и коэффициентом к= a u 0 >0.
r , где r – поворот вокруг точки O на угол u 0 , а h – гомотетия с центром О и коэффициентом к= a u 0 >0.

 =
=  = const .
= const .
 log a f ( x ) = log a h ( x ) к уравнению f ( x ) = h ( x ) используется свойство: при одном и том же основании, если логарифмы двух чисел равны, то и числа равны.
log a f ( x ) = log a h ( x ) к уравнению f ( x ) = h ( x ) используется свойство: при одном и том же основании, если логарифмы двух чисел равны, то и числа равны. 1000=10 3 , т.е. 10 x
1000=10 3 , т.е. 10 x  0, следовательно, 1- a m — k =0,
0, следовательно, 1- a m — k =0,
 a>0 (1)
a>0 (1)
 амечание: Вместо системы, полученной в (2), можно решать эквивалентную ей систему U = V
амечание: Вместо системы, полученной в (2), можно решать эквивалентную ей систему U = V Имеет место равносильный переход, выражающий стандартное определение логарифма: a p = b
Имеет место равносильный переход, выражающий стандартное определение логарифма: a p = b
 твет можно записать по-разному:
твет можно записать по-разному:


 твет: можно записать в таком виде lg 3+2 lg 5/ lg 5- lg 3 , или так: lg 75/ lg (5/3) или так: 1+2 log 35/ log 35-1 .
твет: можно записать в таком виде lg 3+2 lg 5/ lg 5- lg 3 , или так: lg 75/ lg (5/3) или так: 1+2 log 35/ log 35-1 .

 x 2 -5 x +4=0 x =4
x 2 -5 x +4=0 x =4 ример 7. lg x + lg ( x +3) = 1
ример 7. lg x + lg ( x +3) = 1
 и заменим выражение log 4 x 2 на log 2
и заменим выражение log 4 x 2 на log 2  . В результате получим равносильное уравнение:
. В результате получим равносильное уравнение:
 так,
так,

 -1
-1 Укажем равносильный переход для показательных уравнений в более общем виде, чем раньше:
Укажем равносильный переход для показательных уравнений в более общем виде, чем раньше:
 p >a q p
p >a q p
 )
)




 (-1/4; 0)
(-1/4; 0)  Так же как и в предыдущем параграфе приведем общий вид равносильных переходов используемых при решении показательных и логарифмических неравенств.
Так же как и в предыдущем параграфе приведем общий вид равносильных переходов используемых при решении показательных и логарифмических неравенств. (x) q(x) >f(x) h(x)
(x) q(x) >f(x) h(x)  Замечание. Последний равносильный переход можно записать следующим образом:
Замечание. Последний равносильный переход можно записать следующим образом:
 q(x)>h(x)
q(x)>h(x) q(x)>h(x)
q(x)>h(x)