ЕГЭ Профиль №15. Логарифмические неравенства
15 заданием профильного ЕГЭ по математике является неравенство. Самым часто встречаемым неравенством, которое предлагают на реальных экзаменах в 15 задание, является логарифмическое неравенство. При решении логарифмических неравенств, в большинстве случаев (но не всегда) необходимо полностью находить область допустимых неравенств. Большая часть логарифмических неравенств, предлагаемых на реальных экзаменах, решается с помощью замен, методом интервалов или разложением на множители. Прежде чем решать логарифмические неравенства необходимо выучить свойства логарифмов, свойства логарифмической функции и уметь решать логарифмические уравнения. В данном разделе представлены логарифмические неравенства (всего 138) разбитые на два уровня сложности. Уровень А — это простейшие логарифмические неравенства, которые являются подготовительными для решения реальных логарифмических неравенств предлагаемых на ЕГЭ по профильной математике. Уровень В — состоит из неравенств, которые предлагали на реальных ЕГЭ и в диагностических работах прошлых лет.
Логарифмические уравнения и неравенства
Логарифмическим уравнениям и неравенствам в вариантах ЕГЭ по математике посвящена задача C3. Научиться решать задания C3 из ЕГЭ по математике должен каждый ученик, если он хочет сдать предстоящий экзамен на «хорошо» или «отлично». В данной статье представлен краткий обзор часто встречающихся логарифмических уравнений и неравенств, а также основных методов их решения.
Итак, разберем сегодня несколько примеров логарифмических уравнений и неравенств, которые предлагались учащимся в вариантах ЕГЭ по математике прошлых лет. Но начнет с краткого изложение основных теоретических моментов, которые нам понадобятся для их решения.
Логарифмическая функция
Определение
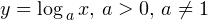
называют логарифмической функцией.
Основные свойства
Основные свойства логарифмической функции y = loga x:
| | a > 1 | 0 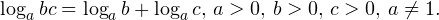 0,\, b>0,\, c>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/> 0,\, b>0,\, c>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>• Логарифм частного двух положительных чисел равен разности логарифмов этих чисел:
• Если a и b — положительные числа, причем a ≠ 1, то для любого числа r справедливо равенство:
• Если a, b, c — положительные числа, причем a и c отличны от единицы, то имеет место равенство (формула перехода к новому основанию логарифма):
Решение логарифмических уравнений и неравенствПример 1. Решите уравнение: Решение. В область допустимых значений входят только те x, при которых выражение, находящееся под знаком логарифма, больше нуля. Эти значения определяются следующей системой неравенств:
С учетом того, что получаем промежуток, определяющий область допустимых значений данного логарифмического уравнения: На основании теоремы 1, все условия которой здесь выполнены, переходим к следующему равносильному квадратичному уравнению: В область допустимых значений входит только первый корень. Ответ: x = 7. Пример 2. Решите уравнение: Решение. Область допустимых значений уравнения определяется системой неравенств:
Очевидно, что эти два условия противоречат друг другу. То есть нет ни одного такого значения x, при котором одновременно выполнялись бы оба неравенства. Область допустимых значений уравнения является пустым множеством, а значит решений у данного логарифмического уравнения нет. Ответ: корней нет. Обратите внимание, что в этом задании нам вообще не пришлось искать корни уравнения. Достаточно оказалось определить, что его область допустимых значений не содержит ни одного действительно числа. Это одно из преимуществ такой последовательности решения логарифмических уравнений и неравенств (начинать с определения области допустимых значений уравнения, а затем решать его путем равносильных преобразований). Примет 3. Решите уравнение: Решение. Область допустимых значений уравнения определяется здесь легко: x > 0. Уравнение принимает вид: Оба ответа входят в область допустимых значений уравнения, поскольку являются положительными числами. Пример 4. Решите уравнение: Решение. Вновь начнем решение с определения области допустимых значений уравнения. Она определяется следующей системой неравенств:
Воспользовавшись правилом сложения логарифмов, переходим к равносильному в области допустимых значений уравнению: Основания логарифмов одинаковы, поэтому в области допустимых значений можно перейти к следующему квадратному уравнению: Первый корень не входит в область допустимых значений уравнения, второй — входит. Ответ: x = -1. Пример 5. Решите уравнение: Решение. Будем искать решения в промежутке x > 0, x≠1. Преобразуем уравнение к равносильному: Оба ответа входят в область допустимых значений уравнения. Пример 6. Решите уравнение: Решение. Система неравенств, определяющая область допустимых значений уравнения, имеет на этот раз вид: Используя свойства логарифма, преобразуем уравнение к равносильному в области допустимых значений уравнению: Используя формулу перехода к новому основанию логарифма, получаем: В область допустимых значений входит только один ответ: x = 4. Перейдем теперь к логарифмическим неравенствам. Это как раз то, с чем вам придется иметь дело на ЕГЭ по математике. Для решения дальнейших примеров нам потребуется следующая теорема: Теорема 2. Если f(x) > 0 и g(x) > 0, то: Решение. Начнем с определения области допустимых значений неравенства. Выражение, стоящее под знаком логарифмической функции, должно принимать только положительные значения. Это значит, что искомая область допустимых значений определяется следующей системой неравенств:
Так как в основании логарифма стоит число, меньшее единицы, соответствующая логарифмическая функция будет убывающей, а потому равносильным по теореме 2 будет переход к следующему квадратичному неравенству: Окончательно, с учетом области допустимых значений получаем ответ: Пример 8. Решите неравенство: Решение. Вновь начнем с определения области допустимых значений:
На множестве допустимых значений неравенства проводим равносильные преобразования: После сокращения и перехода к равносильному по теореме 2 неравенству получаем: С учетом области допустимых значений получаем окончательный ответ: Пример 9. Решите логарифмическое неравенство: Решение. Область допустимых значений неравенства определяется следующей системой:
Видно, что в области допустимых значений выражение, стоящее в основании логарифма, всегда больше единицы, а потому равносильным по теореме 2 будет переход к следующему неравенству: С учетом области допустимых значений получаем окончательный ответ: Пример 10. Решите неравенство: Решение. Область допустимых значений неравенства определяется системой неравенств:
I способ. Воспользуемся формулой перехода к новому основанию логарифма и перейдем к равносильному в области допустимых значений неравенству: Неравенство будет равносильно двум системам. Первой: Итак, окончательный ответ: II способ. Решаем методом интервалов. Преобразуем неравенство к виду: Вычтем из знаменателя С учетом того, что выражения Множество решений данного неравенства Итак, Итак, что нужно для того, чтобы решать логарифмические уравнения и неравенства?
Главное же требование — это настойчивость в достижении своей цели. Учитесь, тренируйтесь, если нужно — ежедневно, изучайте и запоминайте на примерах основные способы решения неравенств и их систем, анализируйте возникающие ошибки и не допускайте их в будущем. За помощью в этом нелегком деле вы можете обратиться к своему школьному учителю по математике, репетитору, родителям, друзьям и знакомым, книгам, а также огромному количеству материалов, доступных на просторах Интернета. Желаю вам успехов в подготовке к Единому государственному экзамену по математике. Тренажёр № 5 (в форме ЕГЭ) Тема: Логарифмические уравнения и неравенства |
| Вложение | Размер |
|---|---|
| trenazher_po_logar.doc | 211 КБ |
Предварительный просмотр:
Тренажёр № 5 (в форме ЕГЭ)
Тема: Логарифмические уравнения и неравенства
(учебник алгебры и начал анализа авторов Ш.А.Алимова и др.)
I уровень сложности
При выполнении заданий А1 – А4 в ответе, выполняемого задания, поставьте цифру соответствующую номеру выбранного вами ответа.
А1. Укажите промежуток, которому принадлежит корень уравнения:
А2. Найдите произведение корней уравнения
А3. Решите неравенство
А4. Решите неравенство:
2)
Ответом к заданиям В1 – В3 должно быть некоторое целое число или число, записанное в виде конечной десятичной дроби. Это число надо записать в ответ.
В1. Решите уравнение: .
В2. Решите уравнение: . В ответе укажите наименьший из корней данного уравнения.
В3. Найдите наибольшее целое значение х , удовлетворяющее неравенству .
Запишите сначала номер выполняемого задания, а затем полное обоснованное решение.
С1. Решите уравнение: .
Тренажёр № 5 (в форме ЕГЭ)
Тема: Логарифмические уравнения и неравенства
(учебник алгебры и начал анализа авторов Ш.А.Алимова и др.)
I уровень сложности
При выполнении заданий А1 – А4 в ответе, выполняемого задания, поставьте цифру соответствующую номеру выбранного вами ответа.
А1. Укажите промежуток, которому принадлежит корень уравнения:
А2. Найдите произведение корней уравнения
А3. Решите неравенство
2)
А4. Решите неравенство:
Ответом к заданиям В1 – В3 должно быть некоторое целое число или число, записанное в виде конечной десятичной дроби. Это число надо записать в ответ.
В1. Решите уравнение: .
В2. Решите уравнение: . В ответе укажите наибольший из корней данного уравнения.
В3. Найдите наименьшее целое значение х , удовлетворяющее неравенству .
Запишите сначала номер выполняемого задания, а затем полное обоснованное решение.
С1. Решите уравнение: .
Тренажёр № 5 (в форме ЕГЭ)
Тема: Логарифмические уравнения и неравенства
(учебник алгебры и начал анализа авторов Ш.А.Алимова и др.)
II уровень сложности
При выполнении заданий А1 – А4 в ответе, выполняемого задания, поставьте цифру соответствующую номеру выбранного вами ответа.
А1. Укажите промежуток, которому принадлежат все корни уравнения:
А2. Найдите сумму всех корней уравнения
А3. Решите неравенство
А4. Решите неравенство:
Ответом к заданиям В1 – В3 должно быть некоторое целое число или число, записанное в виде конечной десятичной дроби. Это число надо записать в ответ.
В1. Решите уравнение: .
В2. Решите уравнение: . В ответе укажите наибольший из корней данного уравнения.
В3. Найдите наименьшее целое значение х , удовлетворяющее неравенству .
Запишите сначала номер выполняемого задания, а затем полное обоснованное решение.
С1. Решите неравенство: .
Тренажёр № 5 (в форме ЕГЭ)
Тема: Логарифмические уравнения и неравенства
(учебник алгебры и начал анализа авторов Ш.А.Алимова и др.)
II уровень сложности
При выполнении заданий А1 – А4 в ответе, выполняемого задания, поставьте цифру соответствующую номеру выбранного вами ответа.
А1. Укажите промежуток, которому принадлежат все корни уравнения:
А2. Найдите сумму всех корней уравнения
А3. Решите неравенство
А4. Решите неравенство:
Ответом к заданиям В1 – В3 должно быть некоторое целое число или число, записанное в виде конечной десятичной дроби. Это число надо записать в ответ.
В1. Решите уравнение: .
В2. Решите уравнение: . В ответе укажите наименьший из корней данного уравнения.
В3. Найдите наибольшее целое значение х , удовлетворяющее неравенству .
Запишите сначала номер выполняемого задания, а затем полное обоснованное решение.
С1. Решите неравенство: .
По теме: методические разработки, презентации и конспекты
Урок рефлексии по теме: «Логарифмические уравнения и неравенства» Алгебра 10 класс
На данном уроке поставленна цель повторения основных приёмов и методов решений логарфмических уравнений и неравенств. На уроке представленна презентация учащихся » Из истории возникновения логар.
Презентация по теме «Логарифмические уравнения и неравенства».
Тест по по алгебре по теме: «Логарифмические уравнения. Логарифмические неравенства», 10 класс
С помощью данного теста проверяются предметные знания и навыки по теме: «Решение логарифмических уравнений и их систем», «Решение логарифмических неравенств» по учебнику Ш.А. Алимова «Алгебра и начала.
Самостоятельная работа по теме :»Логарифмические уравнения и неравенства» 11 класс
Самостоятельная работа по теме : «Логарифмические уравнения и неравенства» 11 класс.
Урок — семинар по теме: «Логарифмические уравнения и неравенства».
Разработка урока-семинара с приложениями.
самостоятельная работа по теме Логарифмические уравнения и неравенства
материал для самостоятельной работы по теме Логарифмические уравнения и неравенства в четырех вариантах.
http://yourtutor.info/%D1%80%D0%B5%D1%88%D0%B5%D0%BD%D0%B8%D0%B5-%D0%B7%D0%B0%D0%B4%D0%B0%D1%87-%D1%813-%D0%B5%D0%B3%D1%8D-%D0%BF%D0%BE-%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B5-%D0%BB%D0%BE%D0%B3
http://nsportal.ru/shkola/algebra/library/2018/12/14/trenazhyor-no-5-v-forme-ege-tema-logarifmicheskie-uravneniya-i
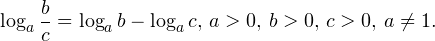 0,\, b>0,\, c>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>
0,\, b>0,\, c>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>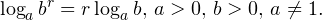 0,\, b>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>
0,\, b>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>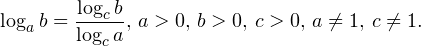 0,\, b>0,\, c>0,\, a\ne 1,\, c\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>
0,\, b>0,\, c>0,\, a\ne 1,\, c\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>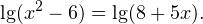
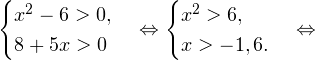 0, \\ 8+5x > 0 \end
0, \\ 8+5x > 0 \end 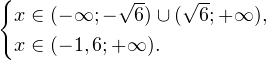
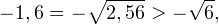 -\sqrt<6>, \]» title=»Rendered by QuickLaTeX.com»/>
-\sqrt<6>, \]» title=»Rendered by QuickLaTeX.com»/>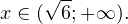
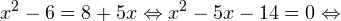
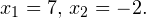
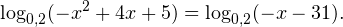
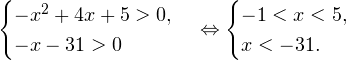 0, \\ -x-31>0 \end
0, \\ -x-31>0 \end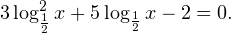
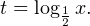
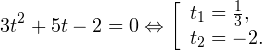
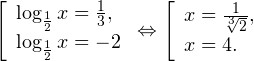
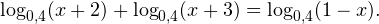
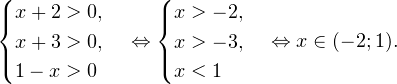 0, \\ x+3>0, \\ 1-x>0 \end
0, \\ x+3>0, \\ 1-x>0 \end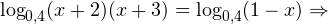
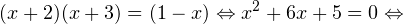
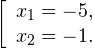
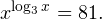
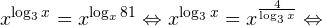
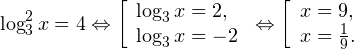
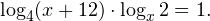
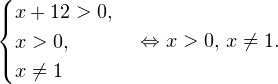 0, \\ x>0, \\ x\ne 1 \end
0, \\ x>0, \\ x\ne 1 \end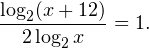
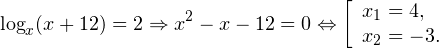
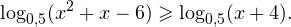
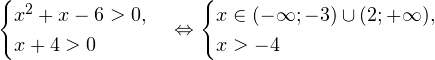 0, \\ x+4>0 \end
0, \\ x+4>0 \end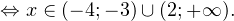
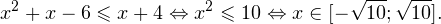
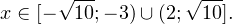
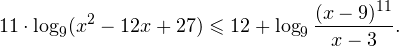
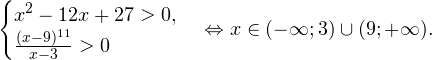 0, \\ \frac<(x-9)^<11>>
0, \\ \frac<(x-9)^<11>>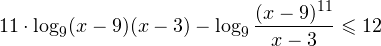
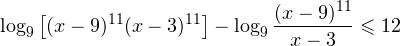
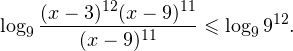
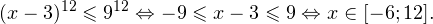
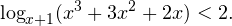
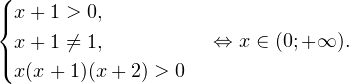 0, \\ x+1\ne 1,\\ x(x+1)(x+2)>0 \end
0, \\ x+1\ne 1,\\ x(x+1)(x+2)>0 \end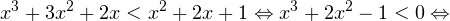
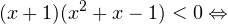
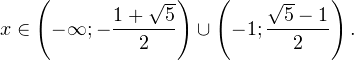
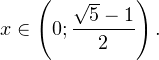
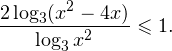
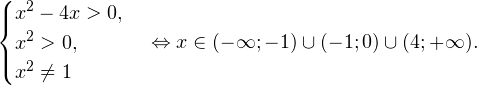 0, \\ x^2>0, \\ x^2\ne 1 \end
0, \\ x^2>0, \\ x^2\ne 1 \end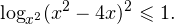
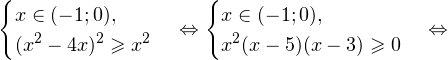
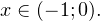
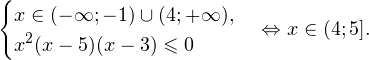
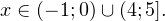
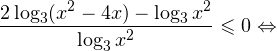
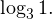 Это ничего не изменит, поскольку
Это ничего не изменит, поскольку 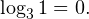
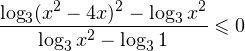
 и
и  — одного знака при
— одного знака при 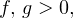 0,» title=»Rendered by QuickLaTeX.com» height=»18″ width=»74″ style=»vertical-align: -4px;»/> в области допустимых значений имеет место следующий равносильный переход:
0,» title=»Rendered by QuickLaTeX.com» height=»18″ width=»74″ style=»vertical-align: -4px;»/> в области допустимых значений имеет место следующий равносильный переход: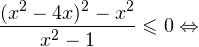
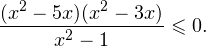
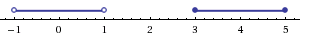
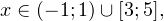 а с учетом области допустимых значений получаем тот же результат:
а с учетом области допустимых значений получаем тот же результат: