Логарифмические уравнения и неравенства
Логарифмическим уравнениям и неравенствам в вариантах ЕГЭ по математике посвящена задача C3. Научиться решать задания C3 из ЕГЭ по математике должен каждый ученик, если он хочет сдать предстоящий экзамен на «хорошо» или «отлично». В данной статье представлен краткий обзор часто встречающихся логарифмических уравнений и неравенств, а также основных методов их решения.
Итак, разберем сегодня несколько примеров логарифмических уравнений и неравенств, которые предлагались учащимся в вариантах ЕГЭ по математике прошлых лет. Но начнет с краткого изложение основных теоретических моментов, которые нам понадобятся для их решения.
Логарифмическая функция
Определение
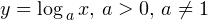
называют логарифмической функцией.
Основные свойства
Основные свойства логарифмической функции y = loga x:
| | a > 1 | 0 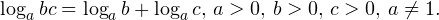 0,\, b>0,\, c>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/> 0,\, b>0,\, c>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>• Логарифм частного двух положительных чисел равен разности логарифмов этих чисел:
• Если a и b — положительные числа, причем a ≠ 1, то для любого числа r справедливо равенство:
• Если a, b, c — положительные числа, причем a и c отличны от единицы, то имеет место равенство (формула перехода к новому основанию логарифма):
Решение логарифмических уравнений и неравенствПример 1. Решите уравнение: Решение. В область допустимых значений входят только те x, при которых выражение, находящееся под знаком логарифма, больше нуля. Эти значения определяются следующей системой неравенств:
С учетом того, что получаем промежуток, определяющий область допустимых значений данного логарифмического уравнения: На основании теоремы 1, все условия которой здесь выполнены, переходим к следующему равносильному квадратичному уравнению: В область допустимых значений входит только первый корень. Ответ: x = 7. Пример 2. Решите уравнение: Решение. Область допустимых значений уравнения определяется системой неравенств:
Очевидно, что эти два условия противоречат друг другу. То есть нет ни одного такого значения x, при котором одновременно выполнялись бы оба неравенства. Область допустимых значений уравнения является пустым множеством, а значит решений у данного логарифмического уравнения нет. Ответ: корней нет. Обратите внимание, что в этом задании нам вообще не пришлось искать корни уравнения. Достаточно оказалось определить, что его область допустимых значений не содержит ни одного действительно числа. Это одно из преимуществ такой последовательности решения логарифмических уравнений и неравенств (начинать с определения области допустимых значений уравнения, а затем решать его путем равносильных преобразований). Примет 3. Решите уравнение: Решение. Область допустимых значений уравнения определяется здесь легко: x > 0. Уравнение принимает вид: Оба ответа входят в область допустимых значений уравнения, поскольку являются положительными числами. Пример 4. Решите уравнение: Решение. Вновь начнем решение с определения области допустимых значений уравнения. Она определяется следующей системой неравенств:
Воспользовавшись правилом сложения логарифмов, переходим к равносильному в области допустимых значений уравнению: Основания логарифмов одинаковы, поэтому в области допустимых значений можно перейти к следующему квадратному уравнению: Первый корень не входит в область допустимых значений уравнения, второй — входит. Ответ: x = -1. Пример 5. Решите уравнение: Решение. Будем искать решения в промежутке x > 0, x≠1. Преобразуем уравнение к равносильному: Оба ответа входят в область допустимых значений уравнения. Пример 6. Решите уравнение: Решение. Система неравенств, определяющая область допустимых значений уравнения, имеет на этот раз вид: Используя свойства логарифма, преобразуем уравнение к равносильному в области допустимых значений уравнению: Используя формулу перехода к новому основанию логарифма, получаем: В область допустимых значений входит только один ответ: x = 4. Перейдем теперь к логарифмическим неравенствам. Это как раз то, с чем вам придется иметь дело на ЕГЭ по математике. Для решения дальнейших примеров нам потребуется следующая теорема: Теорема 2. Если f(x) > 0 и g(x) > 0, то: Решение. Начнем с определения области допустимых значений неравенства. Выражение, стоящее под знаком логарифмической функции, должно принимать только положительные значения. Это значит, что искомая область допустимых значений определяется следующей системой неравенств:
Так как в основании логарифма стоит число, меньшее единицы, соответствующая логарифмическая функция будет убывающей, а потому равносильным по теореме 2 будет переход к следующему квадратичному неравенству: Окончательно, с учетом области допустимых значений получаем ответ: Пример 8. Решите неравенство: Решение. Вновь начнем с определения области допустимых значений:
На множестве допустимых значений неравенства проводим равносильные преобразования: После сокращения и перехода к равносильному по теореме 2 неравенству получаем: С учетом области допустимых значений получаем окончательный ответ: Пример 9. Решите логарифмическое неравенство: Решение. Область допустимых значений неравенства определяется следующей системой:
Видно, что в области допустимых значений выражение, стоящее в основании логарифма, всегда больше единицы, а потому равносильным по теореме 2 будет переход к следующему неравенству: С учетом области допустимых значений получаем окончательный ответ: Пример 10. Решите неравенство: Решение. Область допустимых значений неравенства определяется системой неравенств:
I способ. Воспользуемся формулой перехода к новому основанию логарифма и перейдем к равносильному в области допустимых значений неравенству: Неравенство будет равносильно двум системам. Первой: Итак, окончательный ответ: II способ. Решаем методом интервалов. Преобразуем неравенство к виду: Вычтем из знаменателя С учетом того, что выражения Множество решений данного неравенства Итак, Итак, что нужно для того, чтобы решать логарифмические уравнения и неравенства?
Главное же требование — это настойчивость в достижении своей цели. Учитесь, тренируйтесь, если нужно — ежедневно, изучайте и запоминайте на примерах основные способы решения неравенств и их систем, анализируйте возникающие ошибки и не допускайте их в будущем. За помощью в этом нелегком деле вы можете обратиться к своему школьному учителю по математике, репетитору, родителям, друзьям и знакомым, книгам, а также огромному количеству материалов, доступных на просторах Интернета. Желаю вам успехов в подготовке к Единому государственному экзамену по математике. Логарифмическая функция. Смотр знанийРазделы: Математика
Оборудование: мультимедийный проектор, экран, 2 компьютера с установленной программой “Математика 5–11” Ход урока1. Организационный моментУчитель: Французский писатель Анатоль Франс заметил: “Что учиться можно только весело… Чтобы переварить знания, надо поглощать их с аппетитом”. Последуем совету писателя: будем “поглощать” знания с большим желанием, ведь они скоро вам понадобятся. Цель урока : систематизировать знания по теме “Логарифмическая функция” Приложение 1 ( Слайд 1 ) На уроке рассматриваются пять вопросов:
2. Усвоение знанийВопрос 1: “Существование логарифмической функции”. Еще Аристотель говорил, что определение того или иного понятия, еще не доказывает его существования. Итак, докажем, что логарифмическая функция существует. Ученик 1 (слайд 4) Рассмотрим показательную функцию у = а х , где а ≠ 1, а > 0 Пусть а >1, у = а х непрерывна и возрастает на (– ∞; + ∞). По теореме об обратной функции на промежутке (0; + ∞) определена обратная функция по отношению к показательной, причем она непрерывна и возрастает. Пусть 0 а у = а х непрерывна и убывает на (-∞; + ∞), поэтому на участке (0; + ∞) определена обратная к ней функция. Эта обратная функция – логарифмическая. Функция у = log a x называется логарифмической, где а ≠ 1, а >0, х >0 Вопросы для обсуждения ( задают учащиеся ):
Вопрос 2: “Логарифмические тождества”
Его математические труды направлены на упрощение и упорядочение арифметики, алгебры и тригонометрии. В 1614 году Непер издал труд “Описание удивительной таблицы логарифмов”, в котором не только дал определение логарифма, описал его свойства, но и предложил таблицы логарифмов синусов, косинусов и тангенсов. Также Непер открыл логарифмическую кривую. Позднее им была изобретена логарифмическая линейка, которой пользовались до 70-х годов ХХ в. Какими же основными тождествами мы пользуемся для вычисления? Ученик 2: Логарифмом числа в по основанию а называется показатель степени, в которую нужно возвести основание а, чтобы получить число в
называют основным логарифмическим тождеством.
– логарифм произведения равен сумме логарифмов – логарифм частного равен разности логарифмов – логарифм степени равен произведению показателя степени на логарифм основания этой степени Вопросы для обсуждения: (задают учащиеся)
3 вопрос: “Область определения логарифмической функции”Ученик 3 (слайд 7)
Также, находить область определения выражения
Решением данного неравенства есть множество точек (-∞; –4) v (4; + ∞) Вопросы для обсуждения: (задают учащиеся):
4 вопрос: “Логарифмические уравнения”Ученик 4 ( слайд 8 ) Простейшее логарифмическое уравнение имеет вид log а х = в Логарифмическая функция возрастает или убывает на промежутке (0; + ∞) и принимает на этом промежутке все действительные значения. По теореме о корне, для любого в данное уравнение имеет и притом только одно решение. Теорема: Уравнение вида log а f(х) = log а g(х) равносильно уравнению вида f(х) = g(х) при ограничении
2 х – 4 > 0 |  |
Вопросы для обсуждения (задают ученики):
- всегда нужно находить область определения функции, когда решаем логарифмическое уравнение?
5 вопрос: “Логарифмические неравенства”
Ученик 5 (слайд 9)
- Простейшие логарифмические неравенства имеют вид:
| log 4 | х > log 4 (3 х – 4) х > 3 х – 4 х – 3 х > – 4 – 2 х > – 4 х х
Ответ: 3. ФизкультминуткаМы с вами комплексно повторили знания по теме “Логарифмическая функция”. На следующем этапе урока нам предстоит работать всем сосредоточенно. Внимательны были? Мы рассмотрели логарифмическую функцию у = log a x , если а >1 то функция возрастает. Покажем это.(учитель плавно показывает как функция возрастает).Если 0 у = log 3 x , 4. Проверка знанийПроверку знаний проведем в виде зачета. Одни ученики у нас выступают в роли преподавателей, другие ученики – абитуриенты. Ваша задача: успешно сдать зачет по теме “Логарифмическая функция”. Рассматриваются пять вопросов:
Преподаватели, могут оказывать помощь своим абитуриентам, но для этого нужно будет отдать жетон. Жетонов у каждого абитуриента 3, вопросов 5, так что абитуриенты надейтесь только на свои силы. Результаты сдачи зачета преподаватели будут заносить в контрольный лист. Приложение 2 Зачет начинается. Преподаватели приготовьте свои экзаменационные билеты. Абитуриентам, я желаю удачи, преподавателям хороших результатов, по своим темам. Начало и конец зачета начинаем звонком (колокольчик). 5. Зачетные заданияРабота за компьютером. Программа “Математика. 5–11”
Применяя формулы выполнить задания: Приложение 3 “Область определения логарифмической функции”
6. Итог урокаП.Л.Чебышев говорил: “Сближение теории с практикой дает самые благотворные результаты” Мы с вами сегодня на уроке убедились в справедливости этих слов . ( слайд 10 ) Преподаватели выставляют зачет в контрольные листы абитуриентов. Готовятся к выступлению, характеризуют свою тему, справились абитуриенты с заданиями или нет, пользовались ли подсказкой. Тема, на которую было допущено больше всего ошибок, выносится на доработку на следующие уроки. 7. Домашнее заданиеРабота с учебником М.И. Башмаков, с. 194 (модуль перехода) Вопрос : Как связать между собой степени и логарифмы с разными основаниями? № 55 стр. 225. Решить логарифмические уравнения 1.Найдите промежуток, которому принадлежит корень уравнения log a (1 – х ) = 4 2. Найдите сумму корней уравнения lg(4 х – 3) = 2 lg x Лекция по математике тема: «Логарифмические уравнения»Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах. Тема: Логарифмические уравнения 1. Определение логарифмического уравнения 2. Решение простейших уравнений 4. C ведение уравнений к виду log a f ( x ) = log a g ( x ) с помощью свойств логарифмов по одному основанию. 5. Уравнения вида Alog a f ( x ) + Blog b g ( x ) + C = 0. 6. Введение новой переменной Определение логарифмического уравнения Уравнение, содержащее переменную под знаком логарифма, называется логарифмическим. Простейшим примером логарифмического уравнения служит уравнение вида log a x = b (где а>0, и а ≠1). Функция у= log a x является возрастающей (или убывающей) на промежутке (0; +∞) и принимает на этом промежутке все действительные значения. По теореме о корне) для любого b это уравнение имеет корень, и только один. Решение простейших уравнений Простейшими логарифмическими уравнениями будем называть уравнения следующих видов: Эти уравнения решаются на основании определения логарифма: Решение. Область определения уравнения x > 0. По определению логарифма x = 2 3 , x = 8 принадлежит области определения уравнения. Уравнения данного вида решаются по определению логарифма с учётом области определения функции f ( x ). Уравнение равносильно следующей системе Обычно область определения находится отдельно, и после решения уравнения f ( x ) = a b проверяется, принадлежат ли его корни области определения уравнения. Пример 2.2. log 3 (5х – 1) = 2. Решение: ОДЗ: 5х – 1 > 0; х > 1/5. log 3 (5х– 1) = 2, log 3 (5х – 1) = log 3 3 2 , 5х — 1 =9, Решение. Область определения уравнения находится из неравенства 2 х 2 – 2 х – 1 > 0. Воспользуемся определением логарифма: Применим правила действий со степенями, получим 2 х 2 – 2 х – 1 = 3. Это уравнение имеет два корня х = –1; х = 2. Оба полученные значения неизвестной удовлетворяют неравенству 2 х 2 – 2 х – 1 > 0, т.е. принадлежат области определения данного уравнения, и, значит, являются его корнями. Уравнения этого вида решаются по определению логарифма с учётом области определения уравнения. Данное уравнение равносильно следующей системе Чаще всего, область определения логарифмического уравнения находится отдельно, и после решения уравнения ( f ( x )) c = b или равносильного уравнения проверяется, принадлежат ли его корни найденной области. Решение. Данное уравнение равносильно системе Суть метода заключается в переходе от уравнения не равносильно исходному. На основании свойства монотонности логарифмической функции заключаем, что f ( x ) = g ( x ). Переход от уравнения log a f ( x ) = log a g ( x ) к уравнению f ( x ) = g ( x ) называется потенцированием . Нужно отметить, что при таком переходе может нарушиться равносильность уравнения. В данном уравнении f ( x ) > 0, g ( x ) > 0, а в полученном после потенцирования эти функции могут быть как положительными, так и отрицательными. Поэтому из найденных корней уравнения f ( x ) = g ( x ) нужно отобрать те, которые принадлежат области определения данного уравнения. Остальные корни будут посторонними. Пример 3.1 log 3 ( x 2 – 3 x – 5) = log 3 (7 – 2 x ). Решение. Область определения уравнения найдётся из системы неравенств Потенцируя данное уравнение, получаем х 2 – 3 х – 5 = 7 – 2 х , х 2 – х – 12 = 0, откуда х 1 = –3, х 2 = 4. Число 4 не удовлетворяет системе неравенств. Ответ. х = –3. Если уравнение содержит логарифмы по одному основанию, то для приведения их к виду log a f ( x ) = log a g ( x ) используются следующие свойства логарифмов: Пример 4. 1. log 6 ( x – 1) = 2 – log 6 (5 x + 3). Решение. Найдём область определения уравнения из системы неравенств Применяя преобразования, приходим к уравнению log 6 (( x – 1)(5 x + 3)) = 2, далее, потенцированием, к уравнению ( х – 1)(5 х + 3) = 36, имеющему два корня х = –2,6; х = 3. Учитывая область определения уравнения, х = 3. Ответ. х = 3. Пример 4. 2. Решение. Найдём область определения уравнения, решив неравенство (3 x – 1)( x + 3) > 0 методом интервалов. Учитывая, что разность логарифмов равна логарифму частного, получим уравнение log 5 ( x + 3) 2 = 0. По определению логарифма ( х + 3) 2 = 1, х = –4, х = –2. Число х = –2 посторонний корень. Решение. На области определения 0 x x = x 2 , откуда х = –3, х = 2. Число х = –3 посторонний корень. Метод потенцирования применяется в том случае, если все логарифмы, входящие в уравнение, имеют одинаковое основание. Для приведения логарифмов к общему основанию используются формулы: Пример 5. 1. Решение. Область определения уравнения 1 x Так как 3 = log 2 8, то на области определения получим равносильное уравнение (2– x )/( x –1) = 8, откуда x = 10/9. Ответ. x = 10/9. Пример 5. 2. Решение. Область определения уравнения x > 1. Приведём логарифмы к основанию 3, используя формулу (4). Пример 5. 3. Решение. Область определения уравнения x > –1, x 0. Приведём логарифмы к основанию 3, используя формулу (2). Умножим обе части уравнения на log 3 ( x + 1) 0 и перенесем все слагаемые в левую часть уравнения. Получим ( log 3 ( x + 1)–1) 2 = 0, откуда log 3 ( x + 1) = 1 и Введение новой переменной Рассмотрим два вида логарифмических уравнений, которые введением новой переменной приводятся к квадратным. Уравнения вида Решив его, найдём х из подстановки t = log a f ( x ). Учитывая область определения, выберем только те значения x , которые удовлетворяют неравенству f ( x ) > 0. Пример 6. 1 . lg 2 x – lg x – 6 = 0. Решение. Область определения уравнения – интервал (0; ).Введём новую переменную t = lg x , t R . Уравнение примет вид t 2 – t – 6 = 0. Его корни t 1 = –2, t 2 = 3. Вернёмся к первоначальной переменной lg x = –2 или lg x = 3, х = 10 –2 или х = 10 3 . Оба значения x удовлетворяют области определения данного уравнения ( х > 0).Ответ. х = 0,01; х = 1000. Пример 6. 2 . Решение. Найдём область определения уравнения Применив формулу логарифма степени, получим уравнени е Так как х x | = – x и следовательно Введём новую переменную t = log 3 (– x ), t R . Квадратное уравнение t 2 – 4 t + 4 = 0имеет два равных корня t 1,2 = 2. Вернёмся к первоначальной переменной log 3 (– x ) = 2, отсюда – х = 9, х = –9. Значение неизвестной принадлежит области определения уравнения. Ответ. х = –9. Уравнения вида Уравнения данного вида приводятся к квадратным умножением обеих частей его на log a f ( x ) 0. Учитывая, что log a f ( x ) log f ( x ) a = 1 Замена log a f ( x )= t , tR приводит его к квадратному At 2 + C t + B = 0. Из уравнений log a f ( x )= t 1 , log b f ( x )= t 2 найдем значения x и выберем среди них принадлежащие области определения уравнения: f ( x ) > 0, f ( x ) 1. Пример. 6.3 Решение. Область определения уравнения находим из условий x +2>0, x +2 1 , т.е. x >–2, x –1 . Умножим обе части уравнения на log 5 ( x + 2) 0, получим Возвращаемся к первоначальной переменной: Оба корня принадлежат области определения уравнения. Упражнения для закрепления материала 1) 4) 1. Сформулировать определение логарифмического уравнения. 2. Назвать основные методы решения логарифмических уравнений 1.Ш.А.Алимов, стр. 105-111 2 О.Н.Афанасьева, стор.2753-279 3.А.Г.Мерзляк, стор.202-2 источники: http://urok.1sept.ru/articles/537190 http://infourok.ru/lekciya-po-matematike-tema-logarifmicheskie-uravneniya-716816.html |
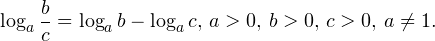 0,\, b>0,\, c>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>
0,\, b>0,\, c>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>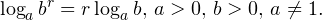 0,\, b>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>
0,\, b>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>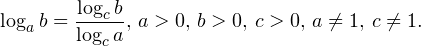 0,\, b>0,\, c>0,\, a\ne 1,\, c\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>
0,\, b>0,\, c>0,\, a\ne 1,\, c\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>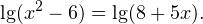
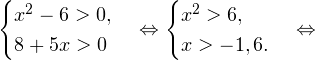 0, \\ 8+5x > 0 \end
0, \\ 8+5x > 0 \end 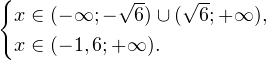
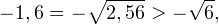 -\sqrt<6>, \]» title=»Rendered by QuickLaTeX.com»/>
-\sqrt<6>, \]» title=»Rendered by QuickLaTeX.com»/>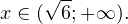
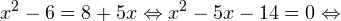
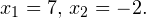
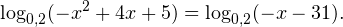
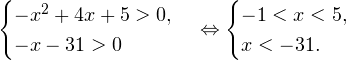 0, \\ -x-31>0 \end
0, \\ -x-31>0 \end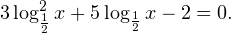
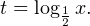
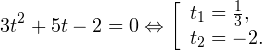
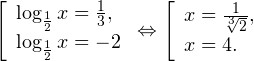
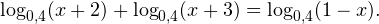
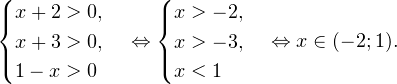 0, \\ x+3>0, \\ 1-x>0 \end
0, \\ x+3>0, \\ 1-x>0 \end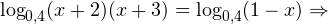
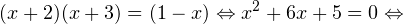
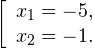
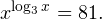
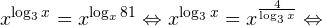
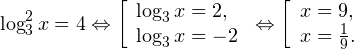
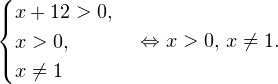 0, \\ x>0, \\ x\ne 1 \end
0, \\ x>0, \\ x\ne 1 \end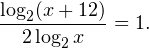
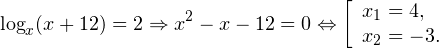
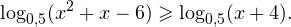
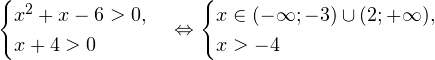 0, \\ x+4>0 \end
0, \\ x+4>0 \end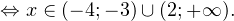
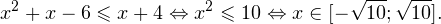
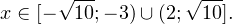
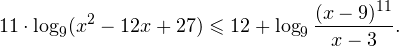
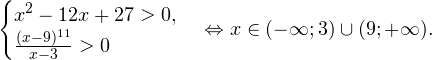 0, \\ \frac<(x-9)^<11>>
0, \\ \frac<(x-9)^<11>>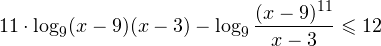
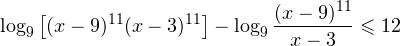
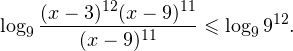
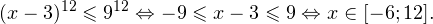
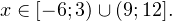
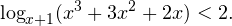
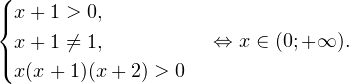 0, \\ x+1\ne 1,\\ x(x+1)(x+2)>0 \end
0, \\ x+1\ne 1,\\ x(x+1)(x+2)>0 \end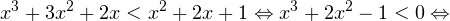
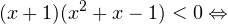
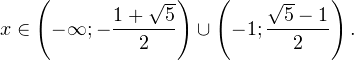
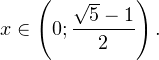
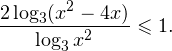
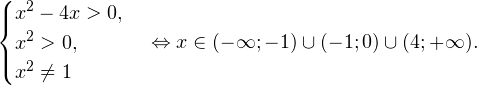 0, \\ x^2>0, \\ x^2\ne 1 \end
0, \\ x^2>0, \\ x^2\ne 1 \end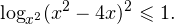
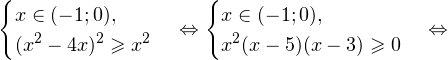
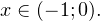
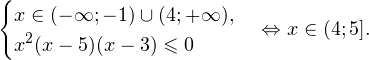
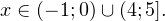
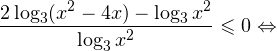
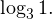 Это ничего не изменит, поскольку
Это ничего не изменит, поскольку 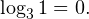
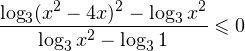
 и
и  — одного знака при
— одного знака при 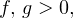 0,» title=»Rendered by QuickLaTeX.com» height=»18″ width=»74″ style=»vertical-align: -4px;»/> в области допустимых значений имеет место следующий равносильный переход:
0,» title=»Rendered by QuickLaTeX.com» height=»18″ width=»74″ style=»vertical-align: -4px;»/> в области допустимых значений имеет место следующий равносильный переход: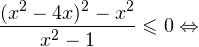
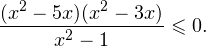
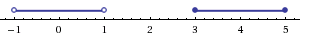
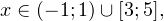 а с учетом области допустимых значений получаем тот же результат:
а с учетом области допустимых значений получаем тот же результат: 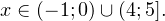









 ; lg 8 + lg 125
; lg 8 + lg 125


 (2 х – 4) = –2
(2 х – 4) = –2 


 , у = log 5 x )
, у = log 5 x ) и график симметричный относительно у = х .
и график симметричный относительно у = х . х и график симметричный относительно у = х .
х и график симметричный относительно у = х .

 (5 +2 ч) = 1;
(5 +2 ч) = 1; (2 х – 5) 0,2 (1 – х ) >1; log 3 (16 – 2 х ) 3 4 х
(2 х – 5) 0,2 (1 – х ) >1; log 3 (16 – 2 х ) 3 4 х > l
> l (2 х – 5) >
(2 х – 5) >




 Ответ. x = 4.
Ответ. x = 4.










 Ответ. х = 6.
Ответ. х = 6.



 где a > 0, a 1, A , В , С – действительные числа .
где a > 0, a 1, A , В , С – действительные числа .



 где a > 0, a 1, A , В , С – действительные числа , A 0, В 0 .
где a > 0, a 1, A , В , С – действительные числа , A 0, В 0 .

 или, заменив log 5 ( x + 2) = t , придем к квадратному уравнению t 2 – t – 2 = 0, t 1 = –1, t 2 =2.
или, заменив log 5 ( x + 2) = t , придем к квадратному уравнению t 2 – t – 2 = 0, t 1 = –1, t 2 =2. ; 2)
; 2)  ; 3)
; 3)  ;
; ; 5)
; 5)  ;
;