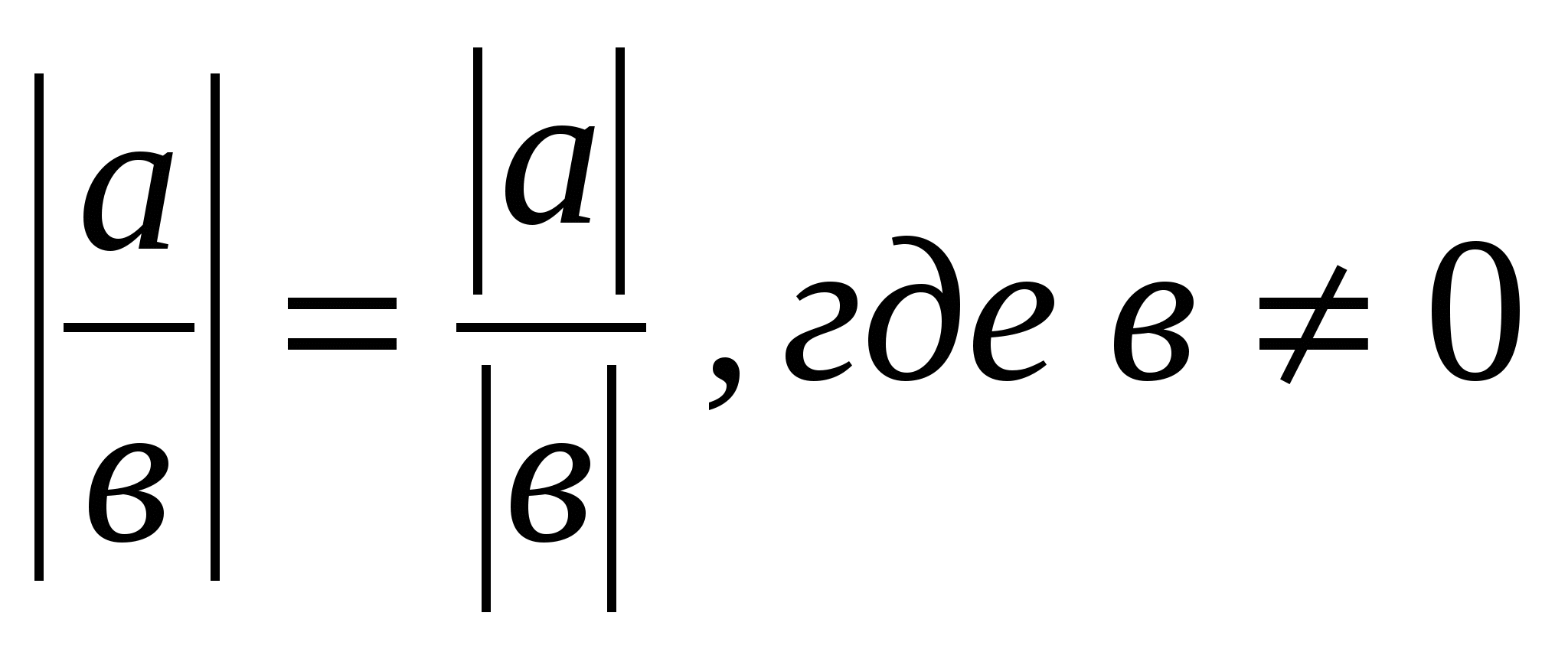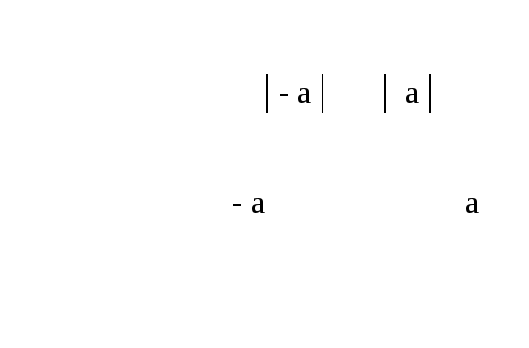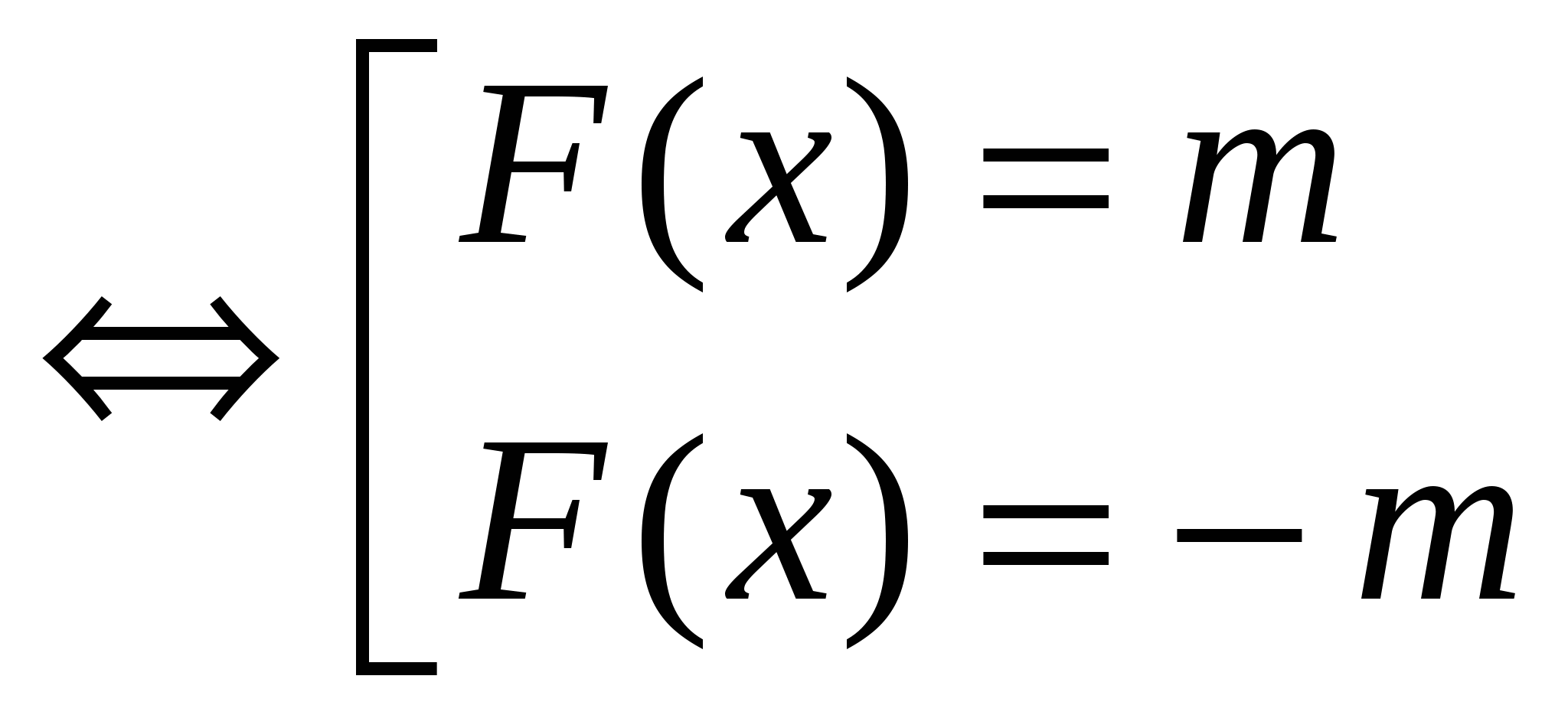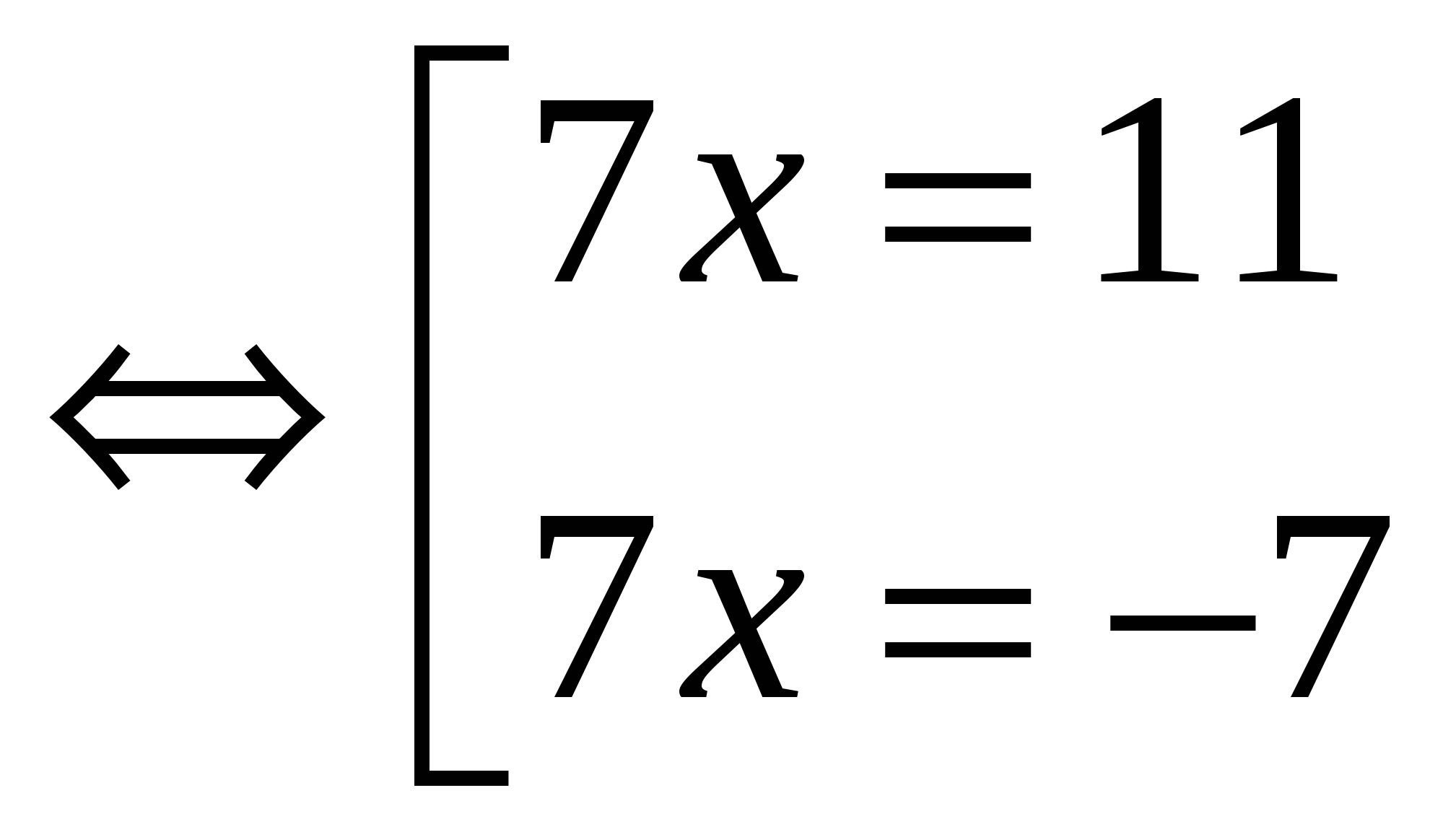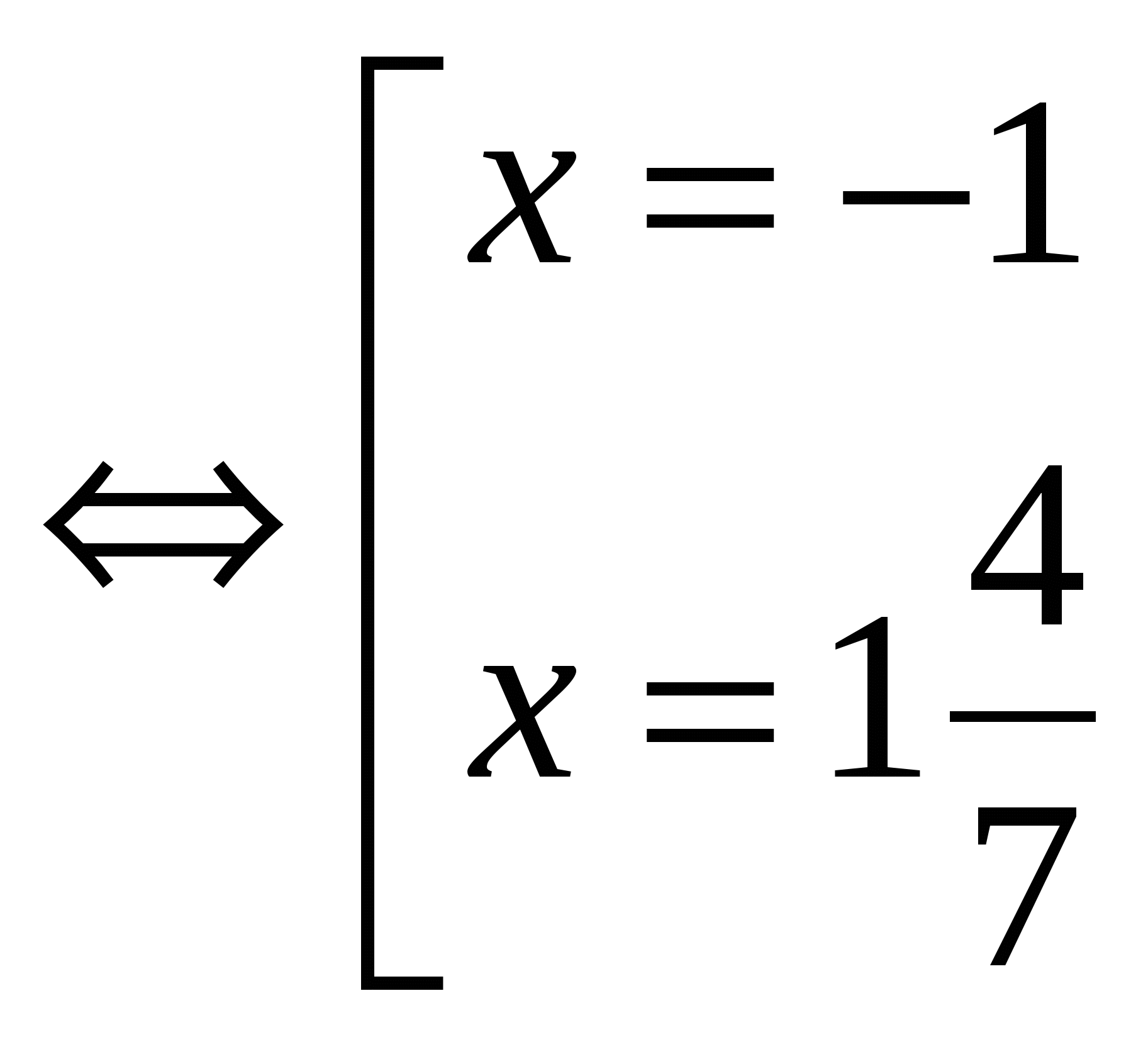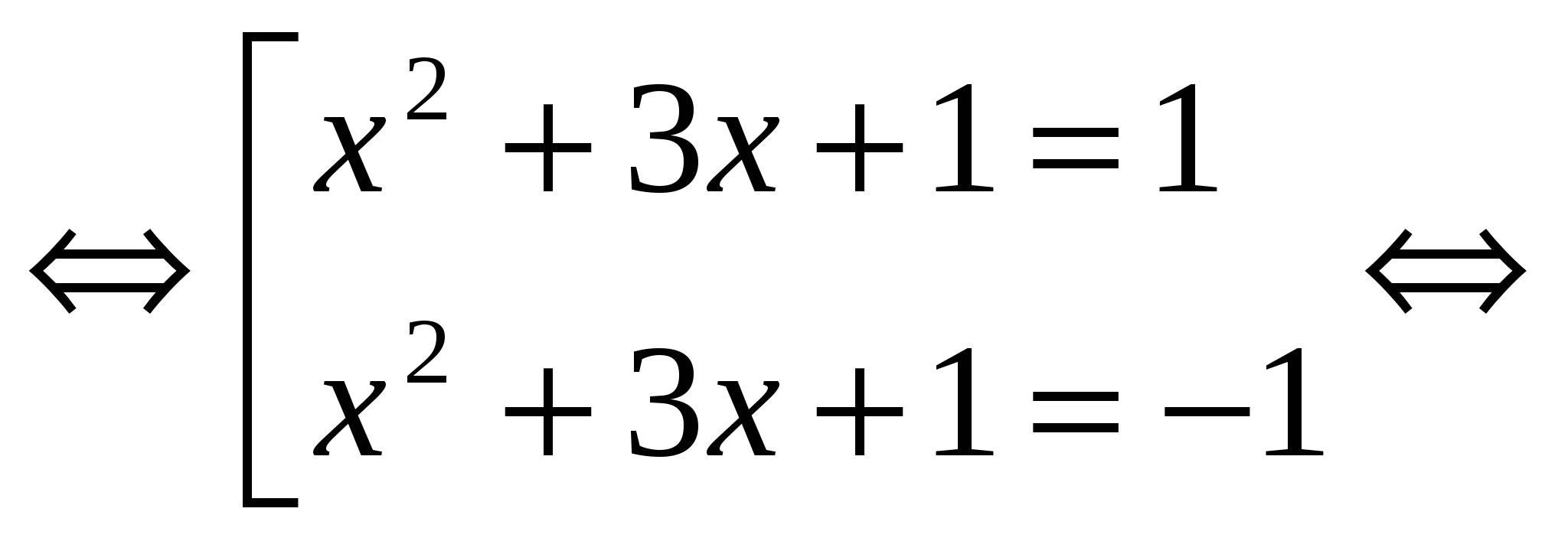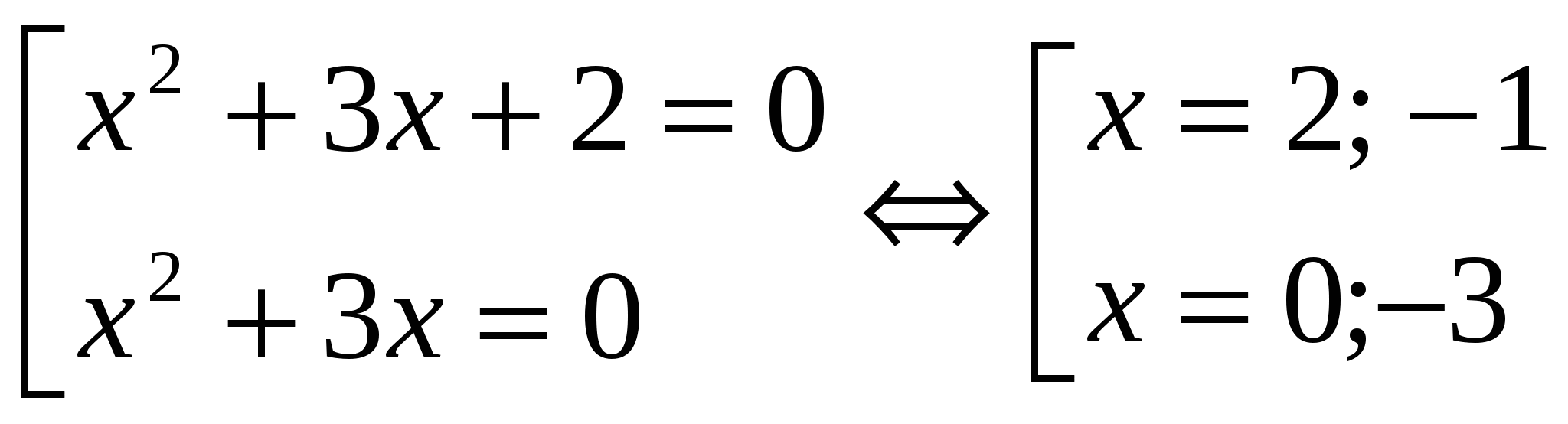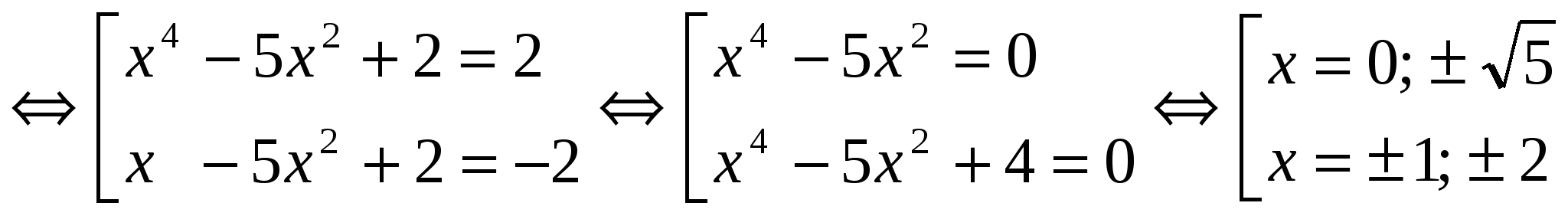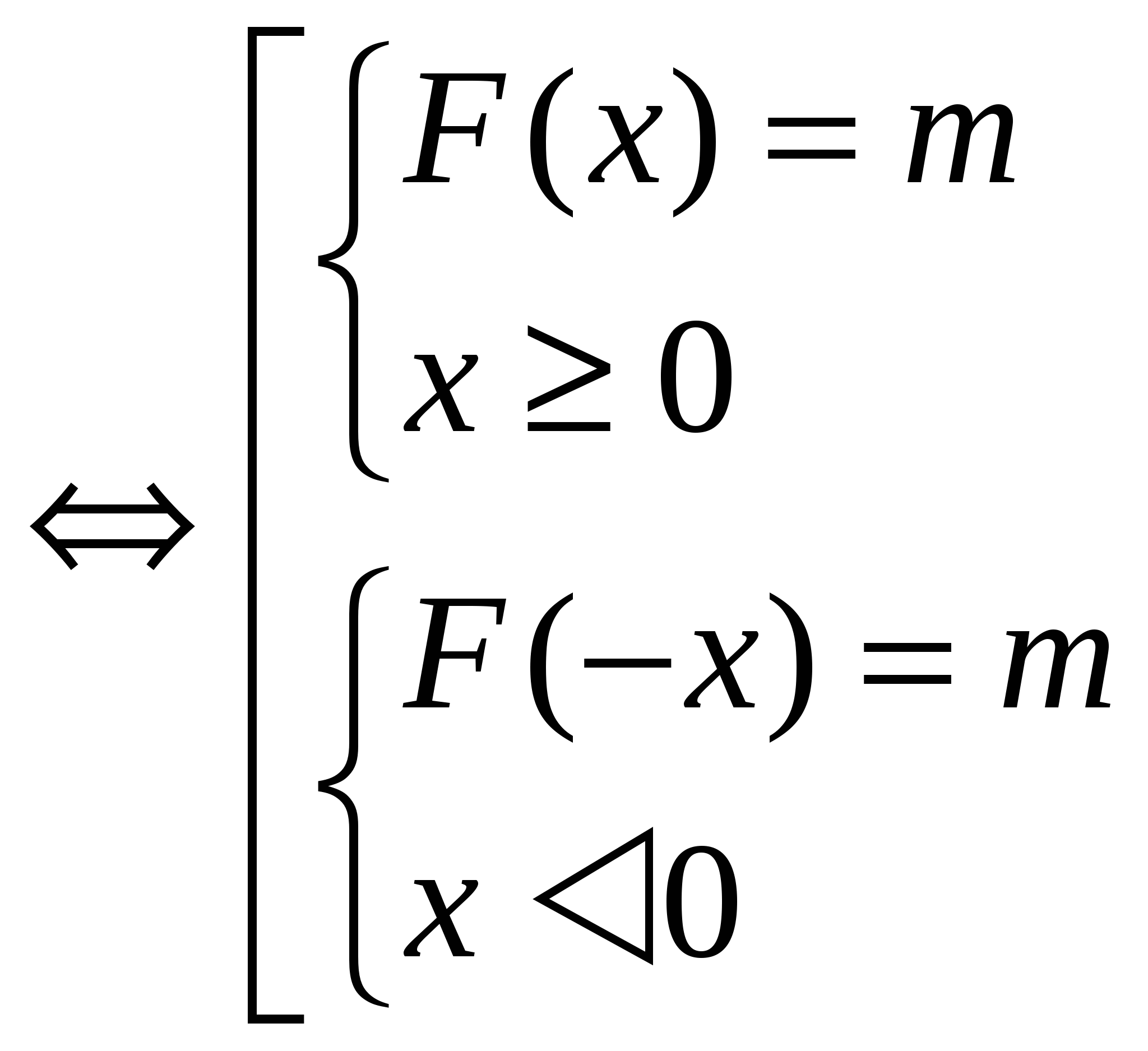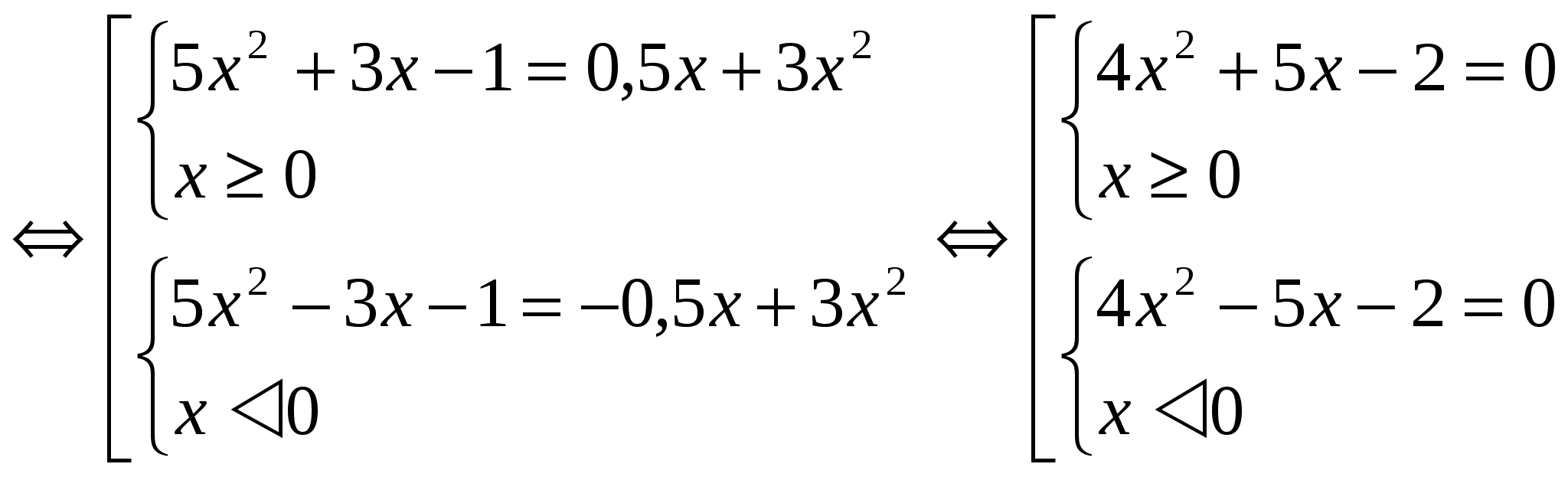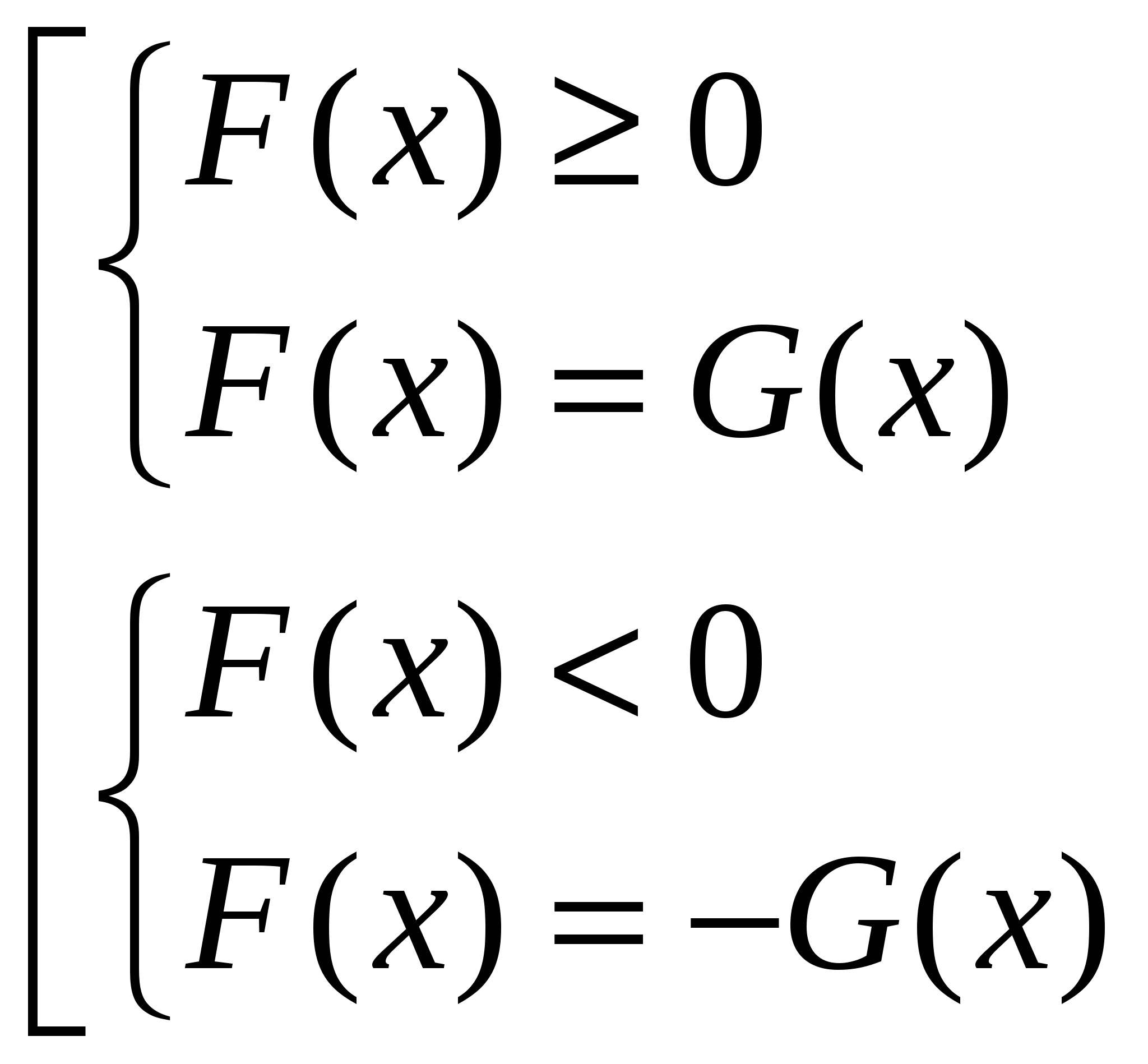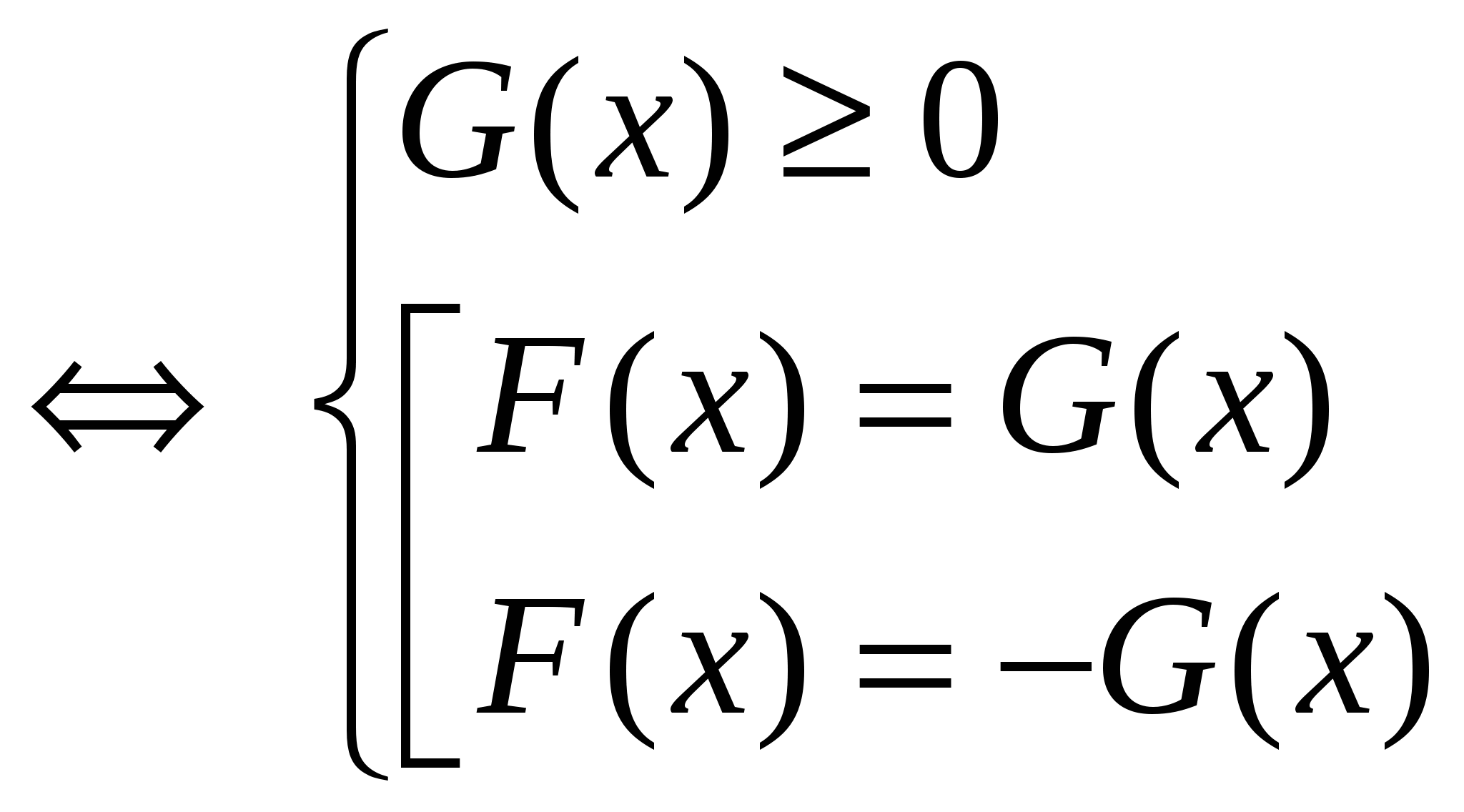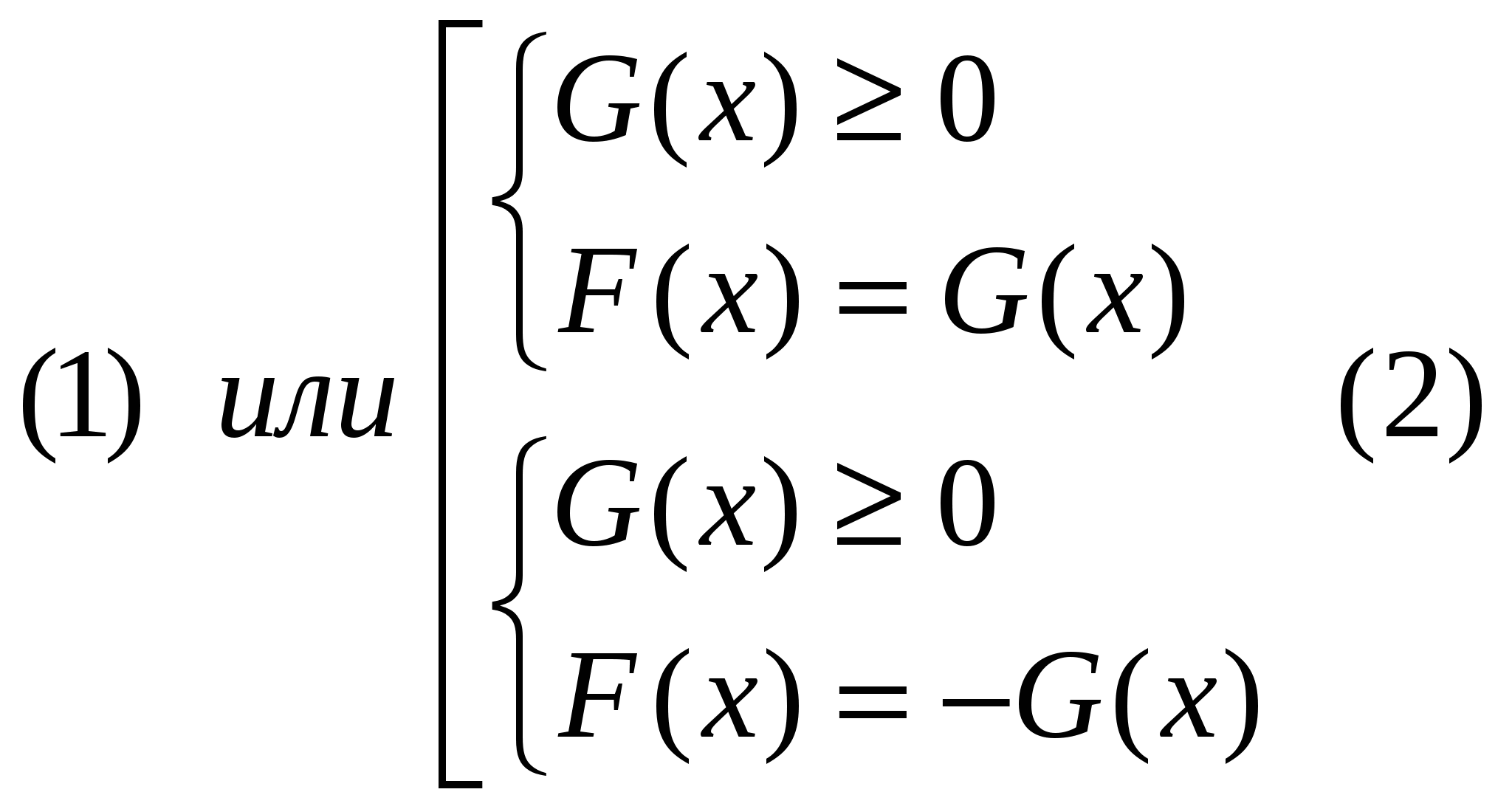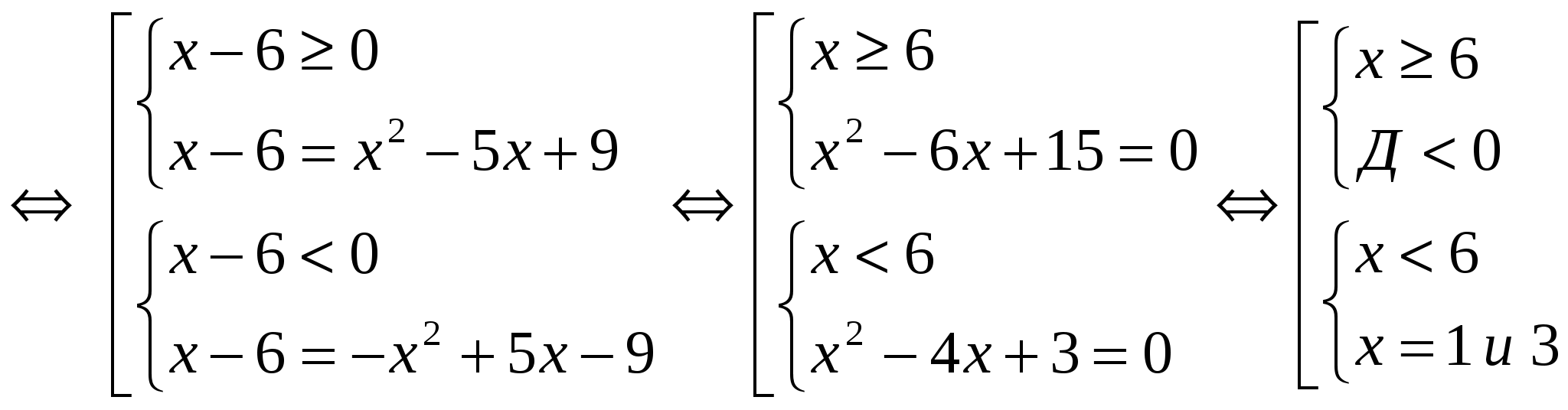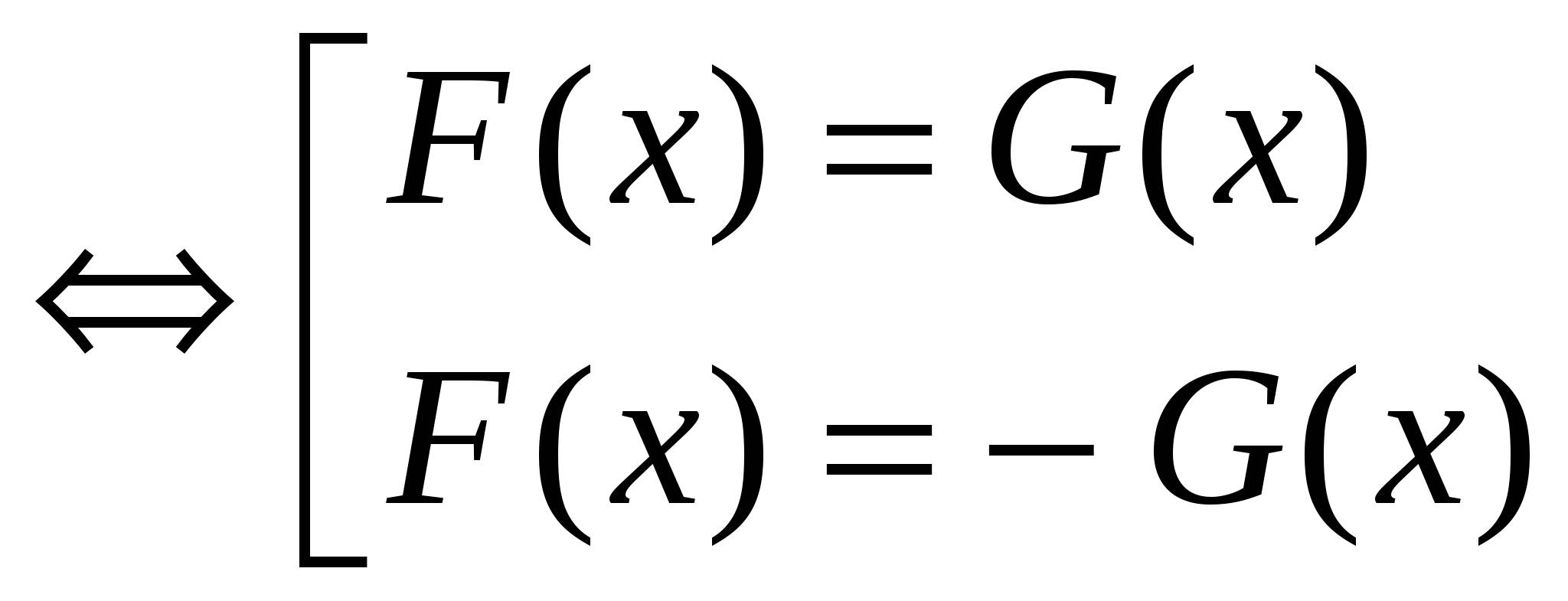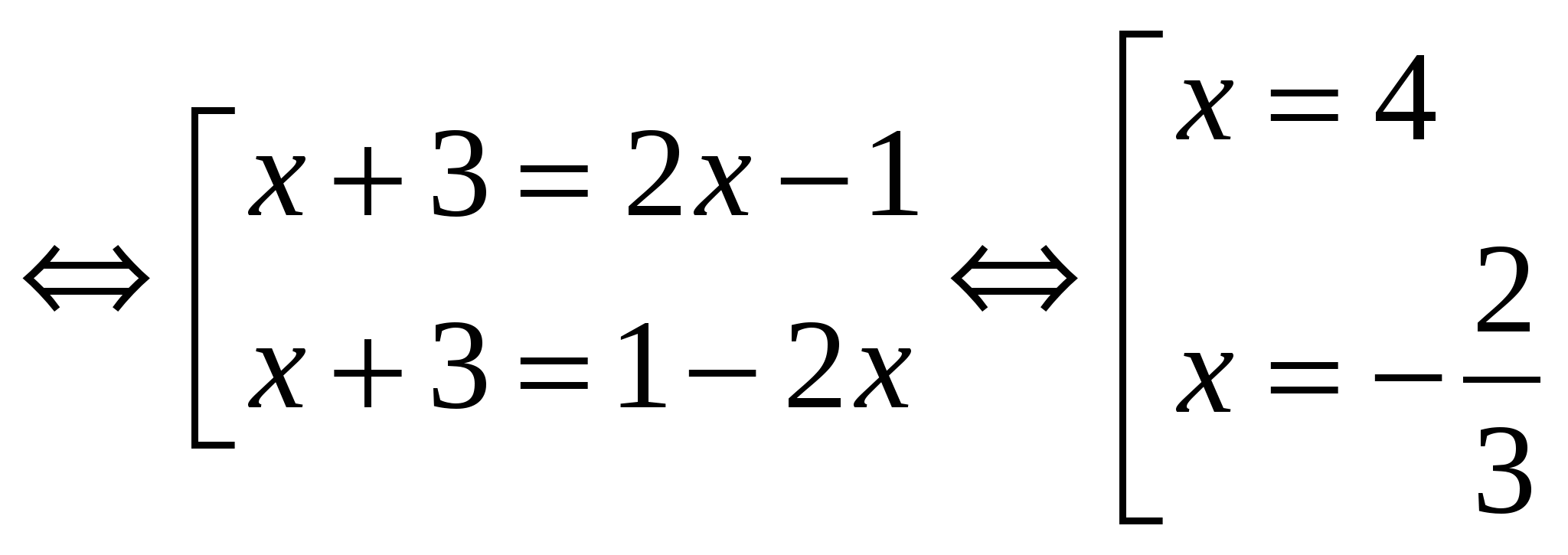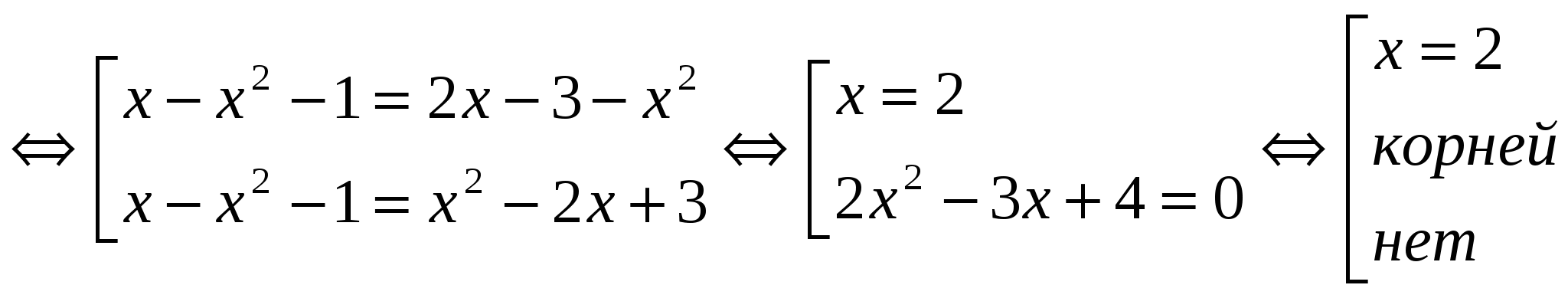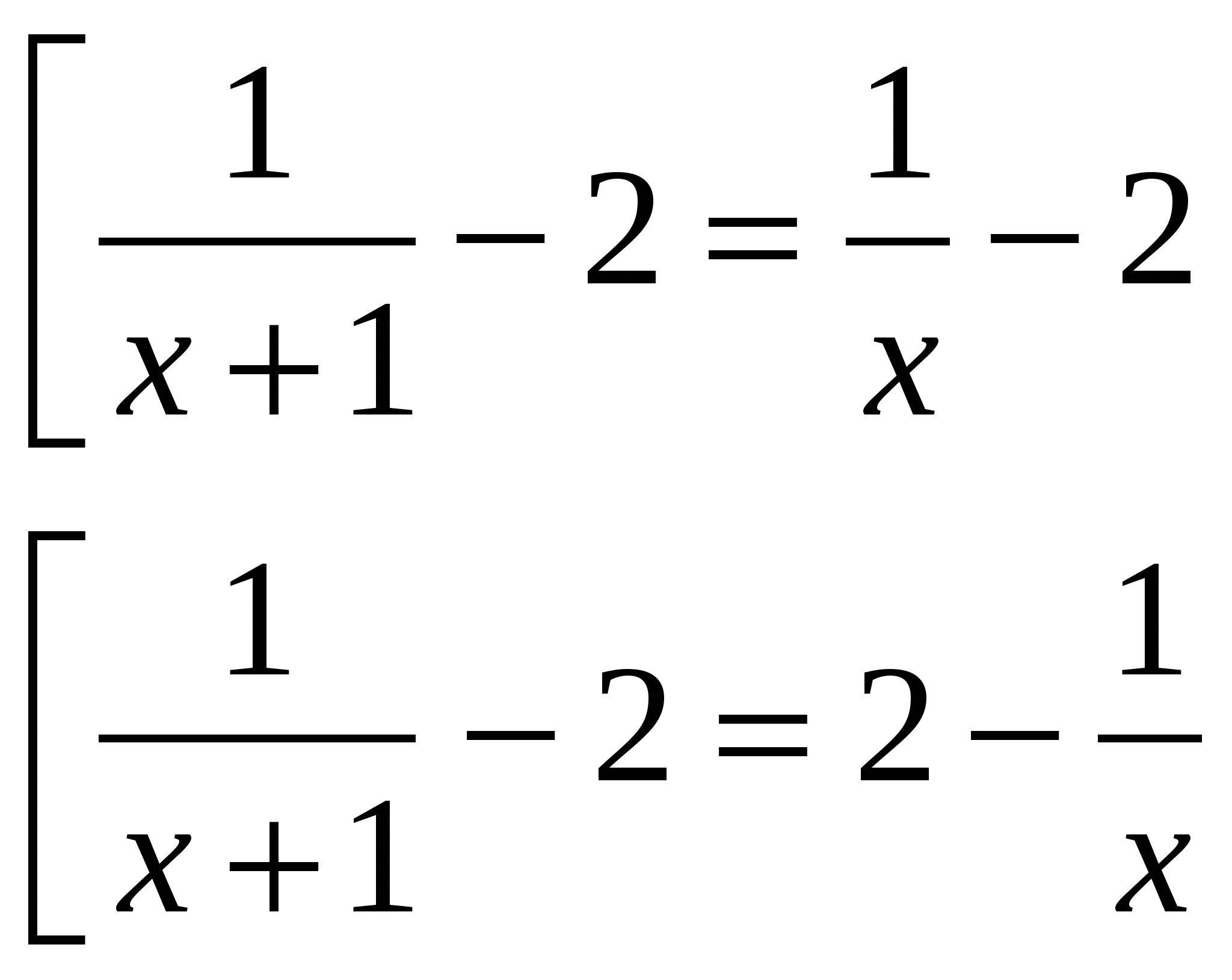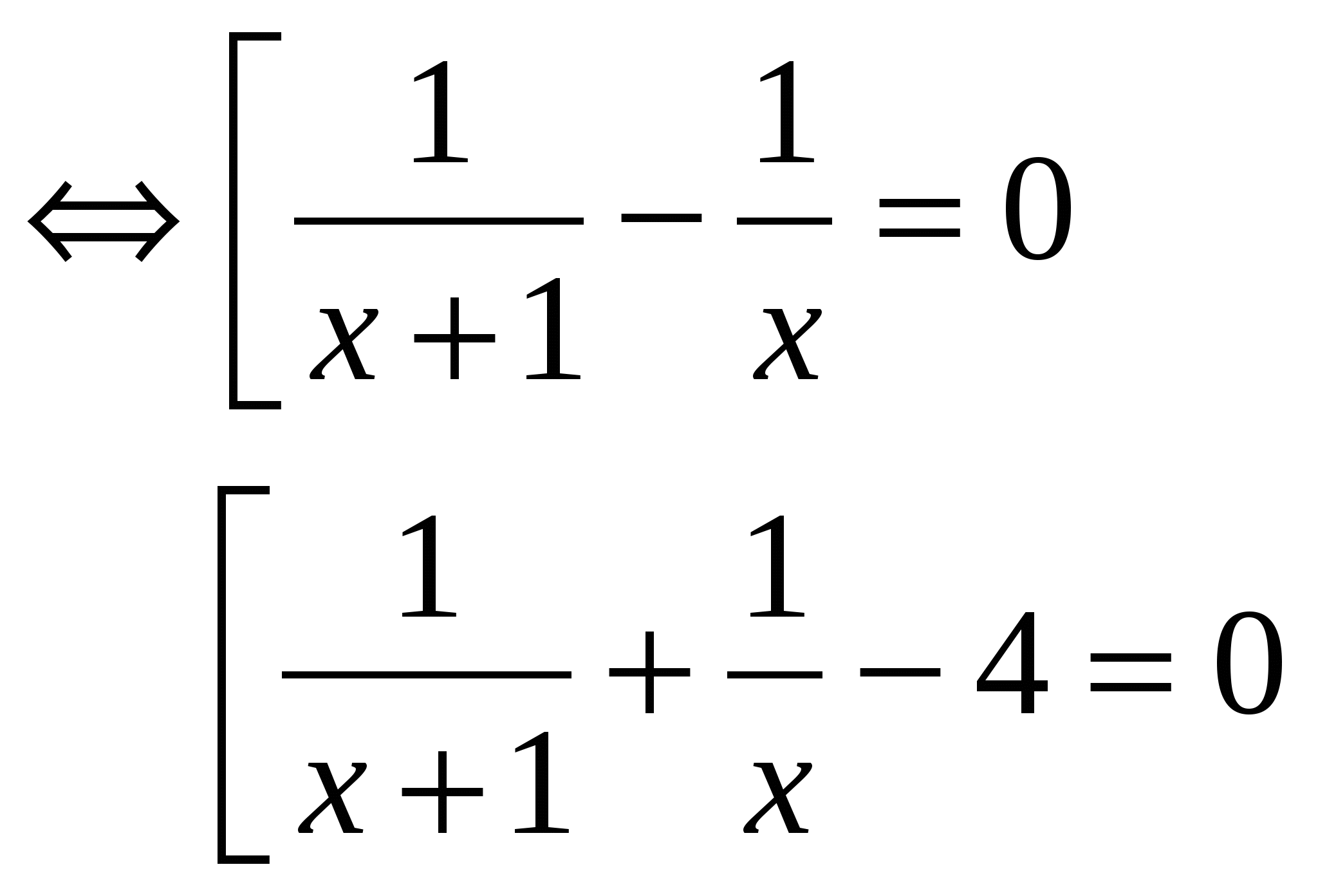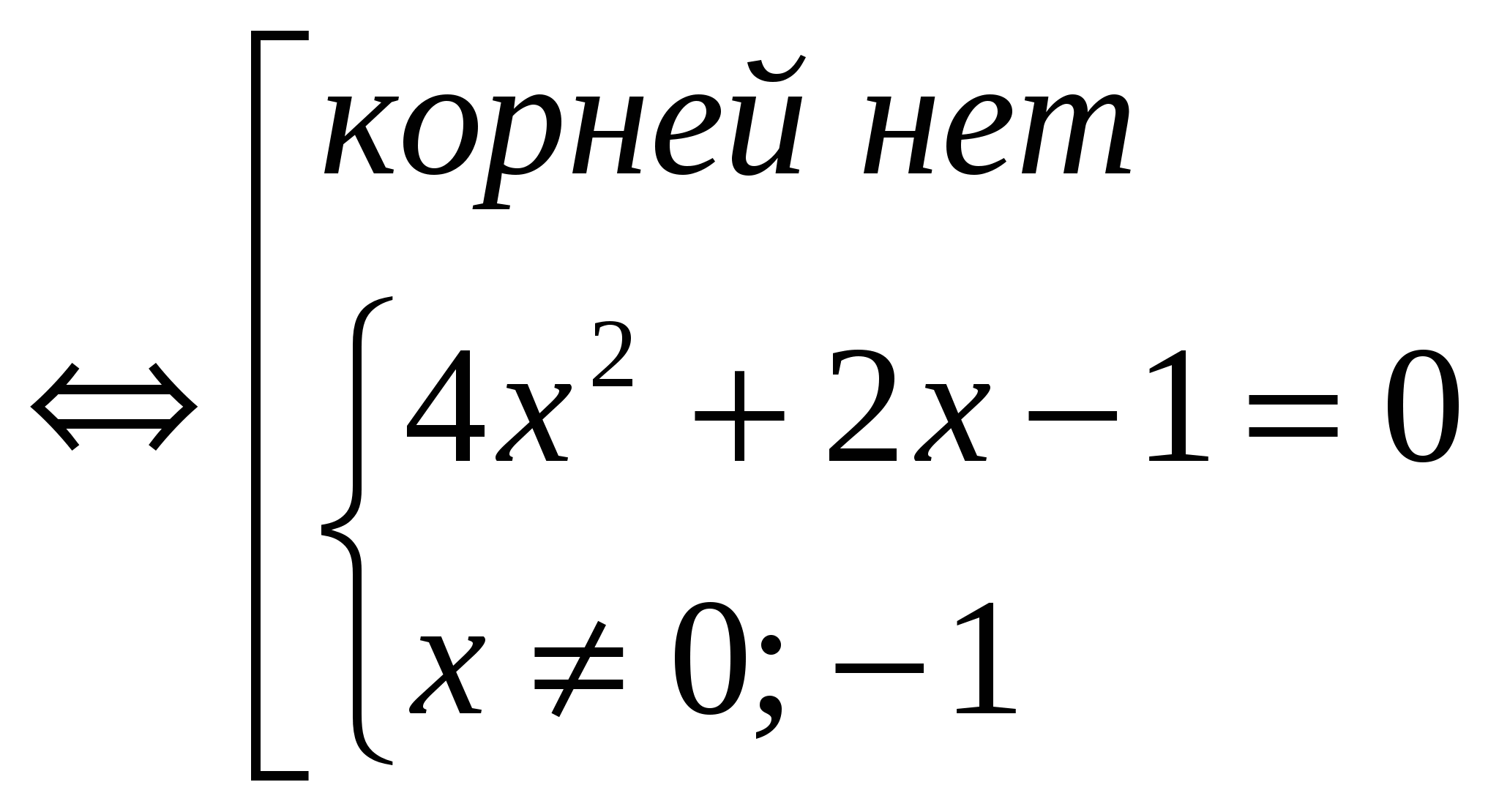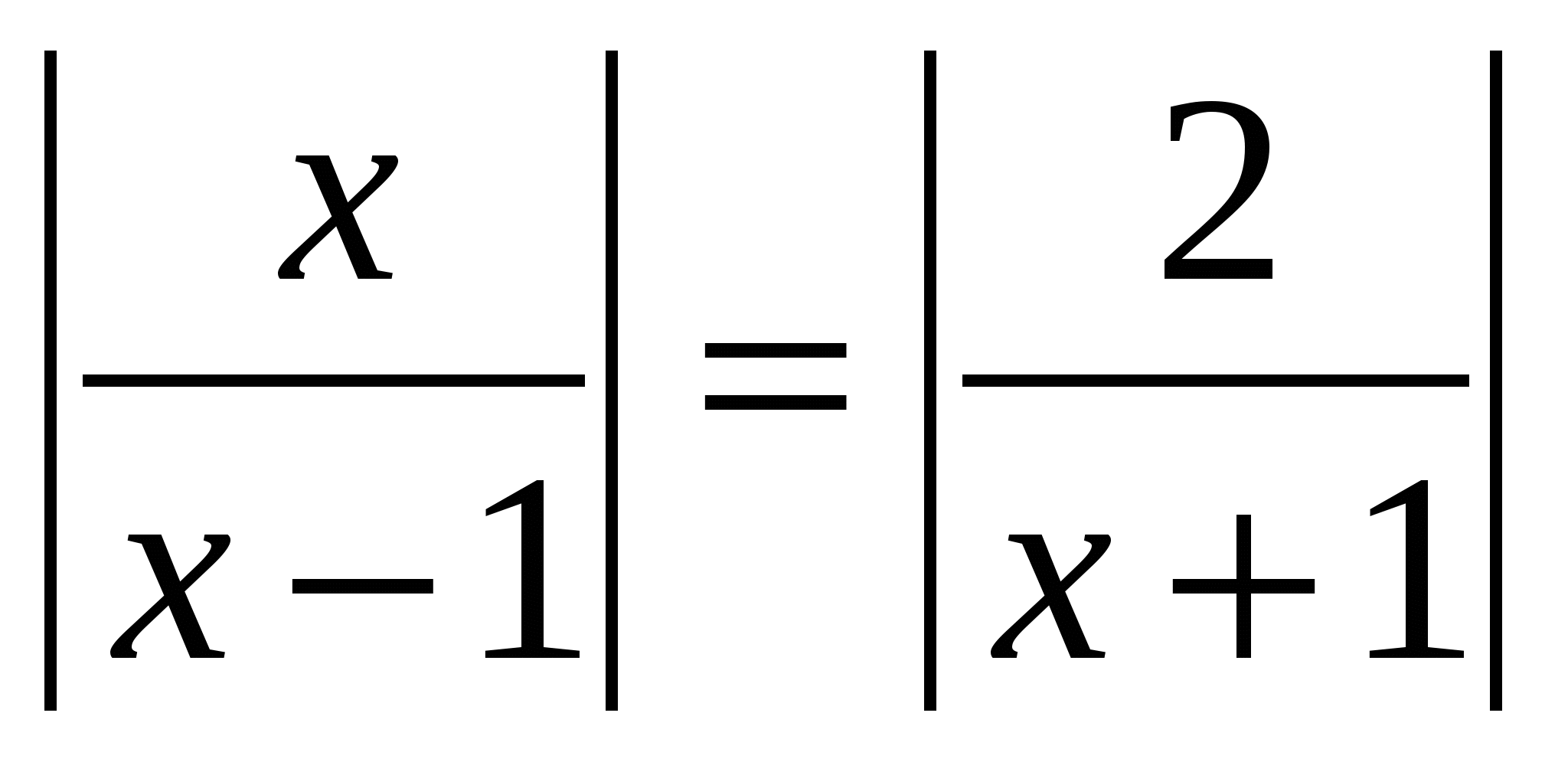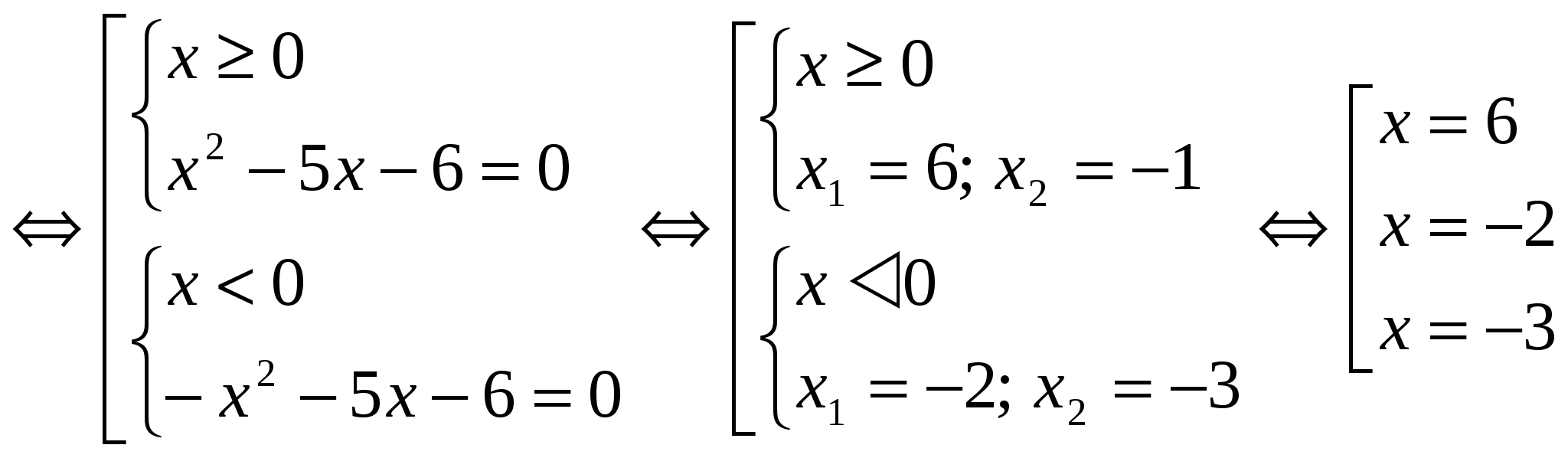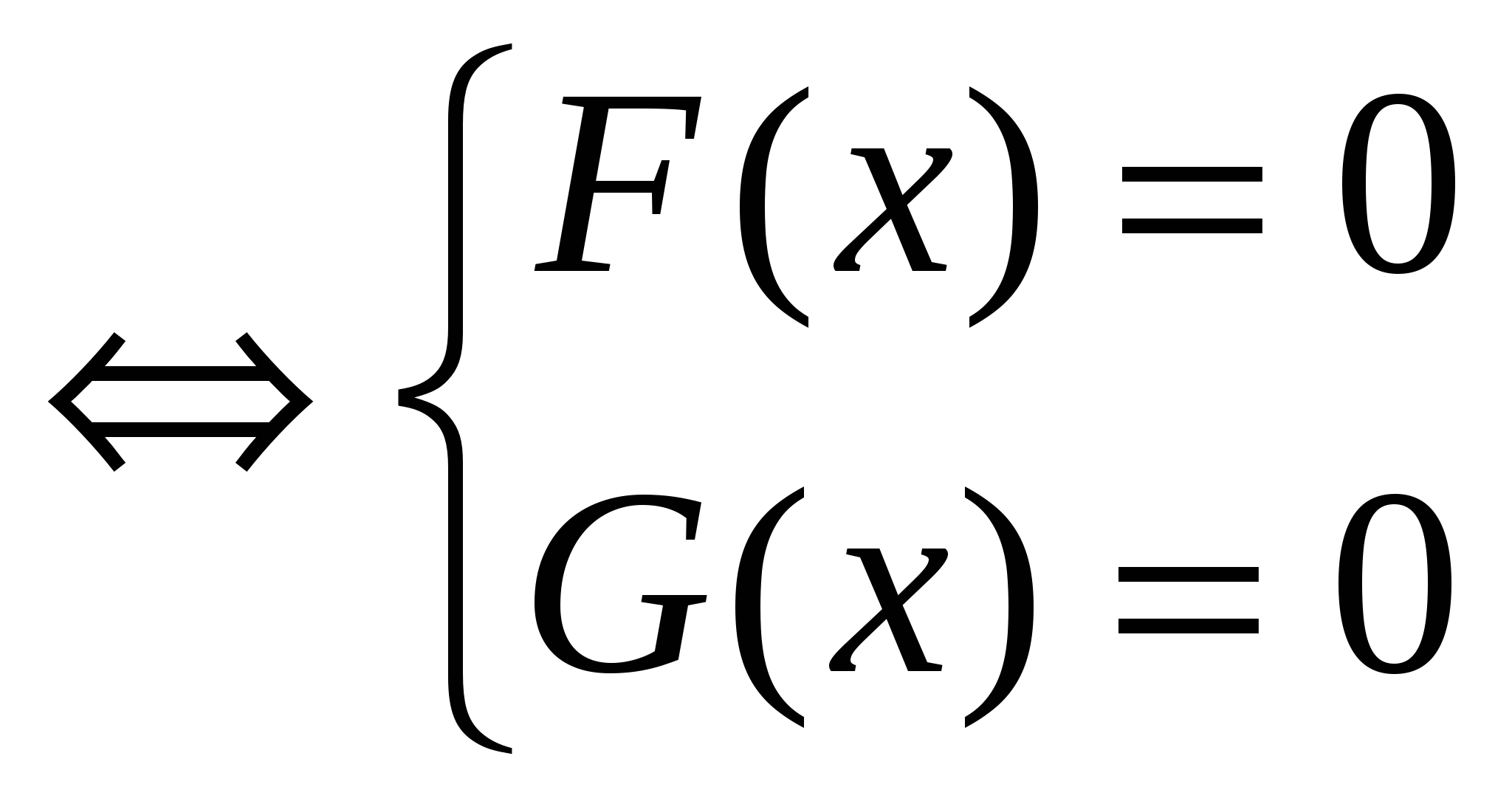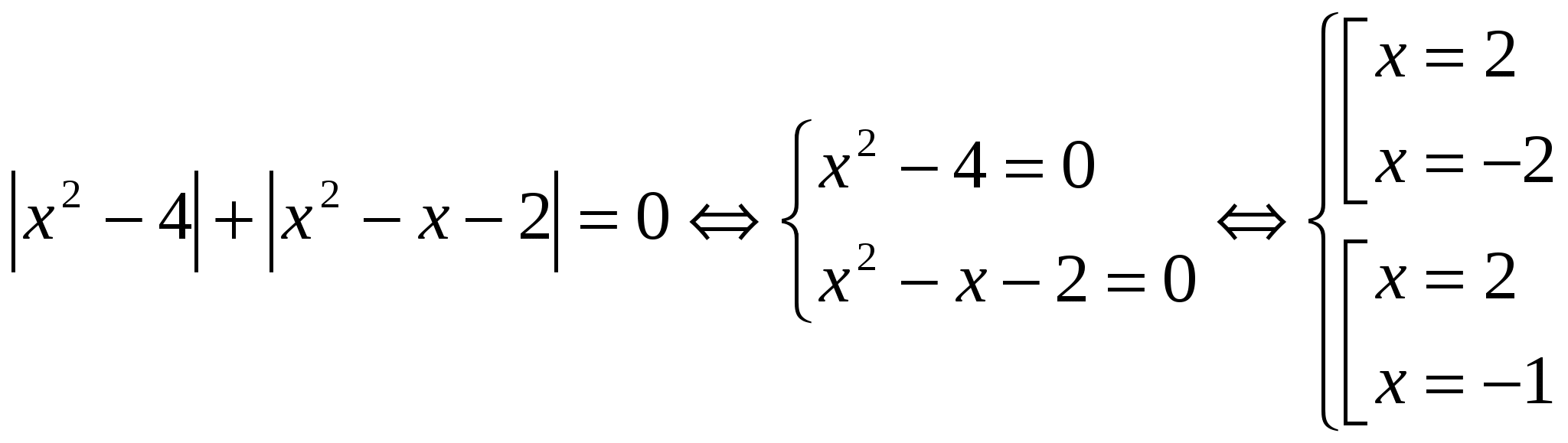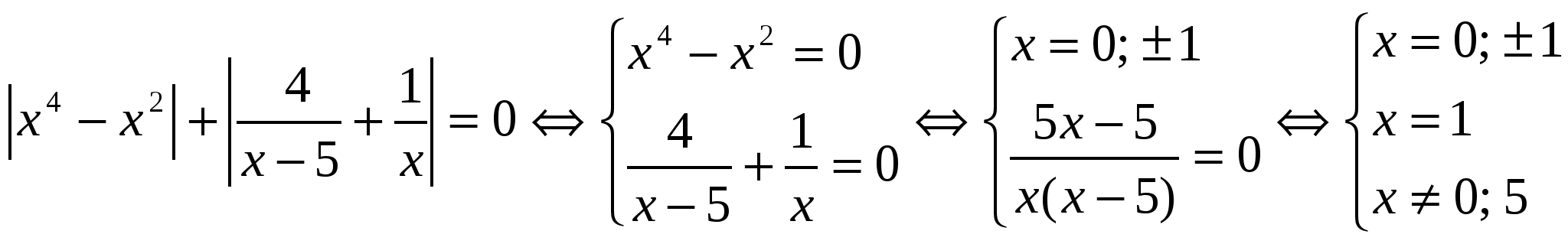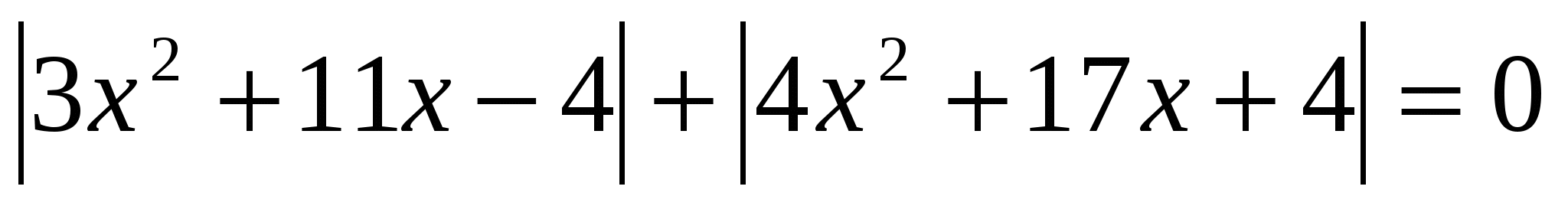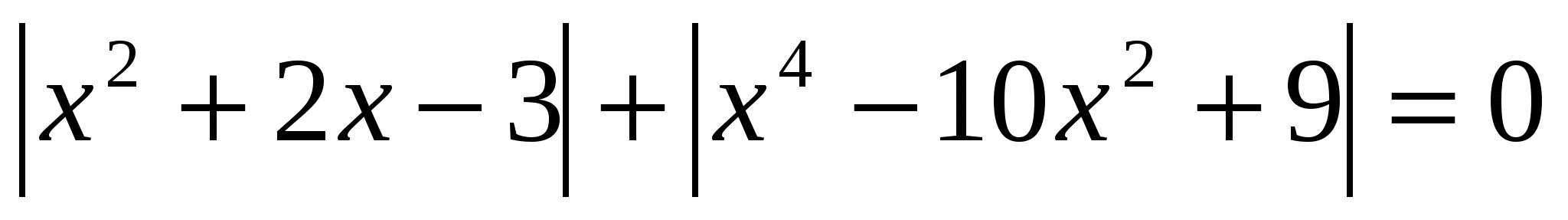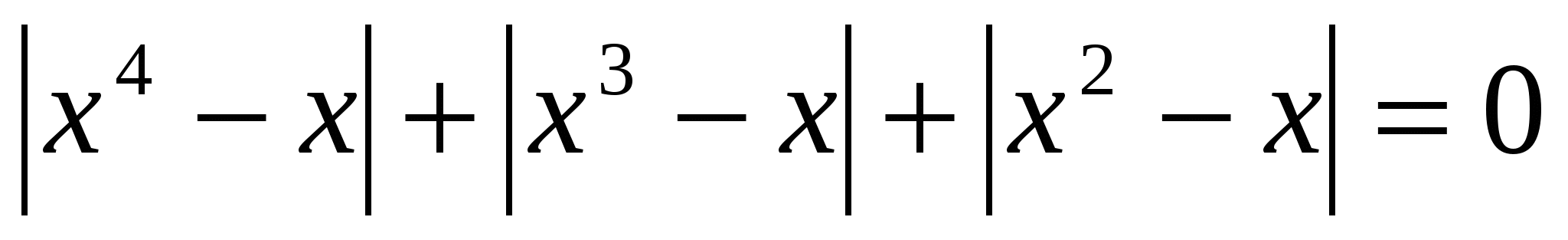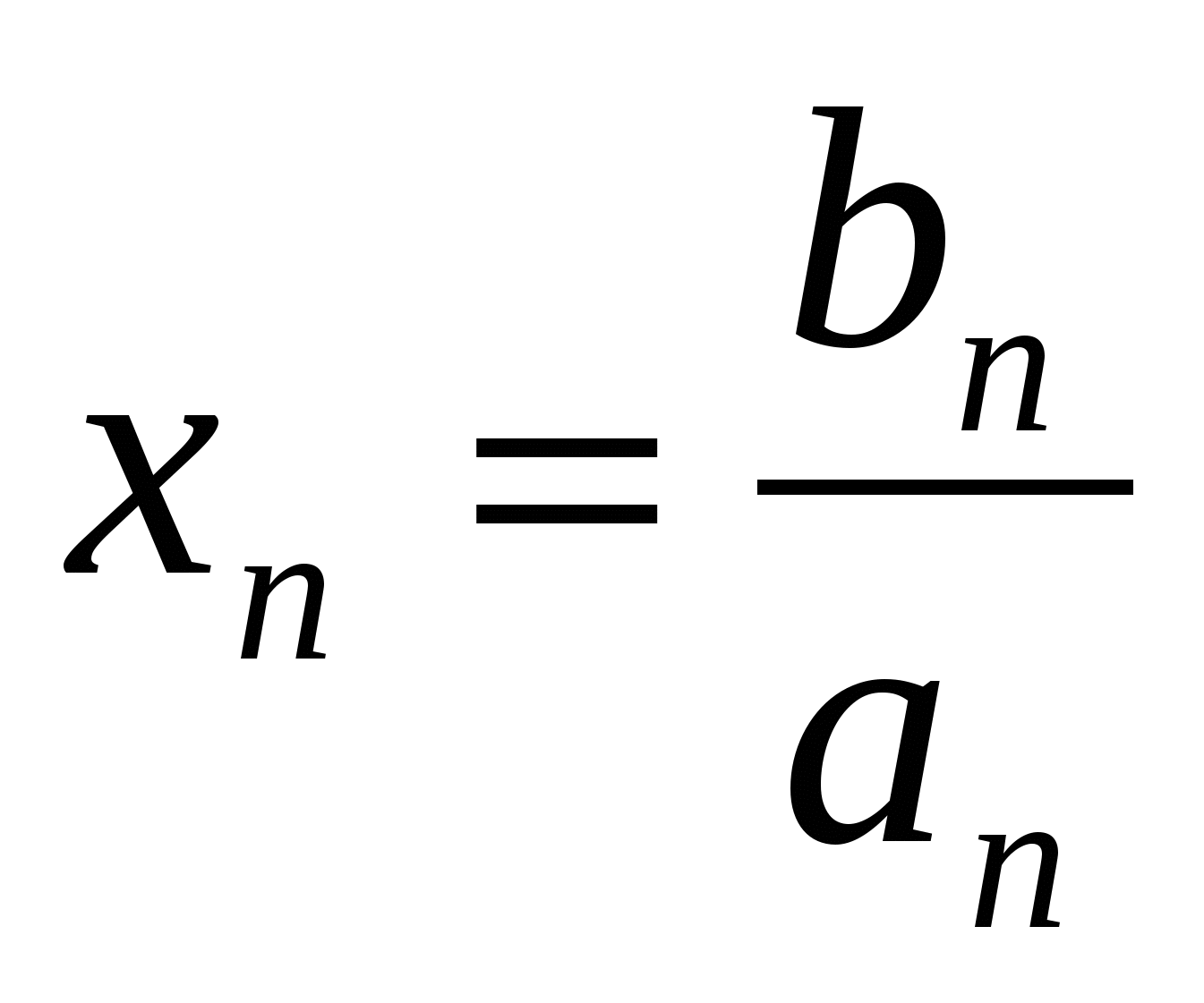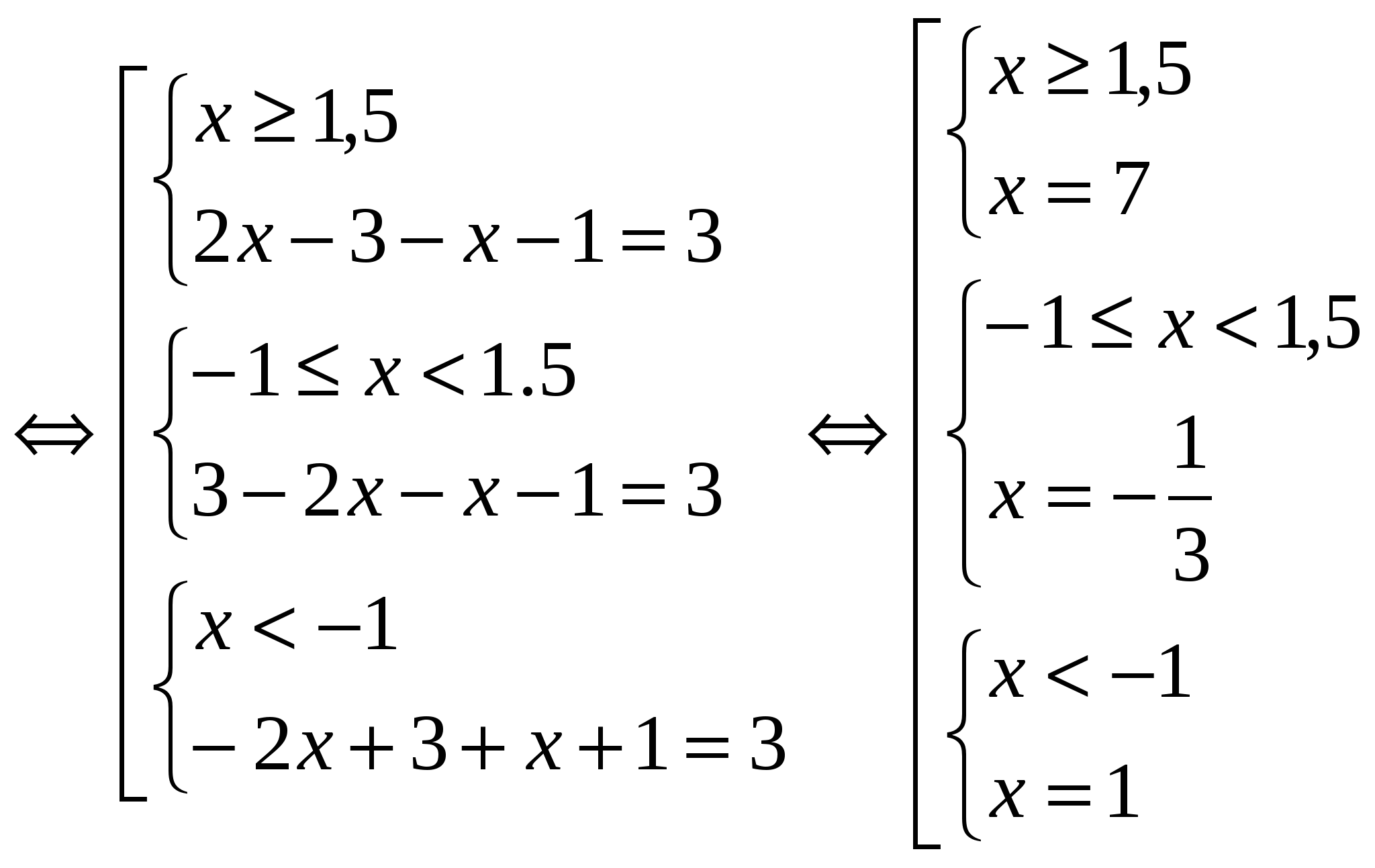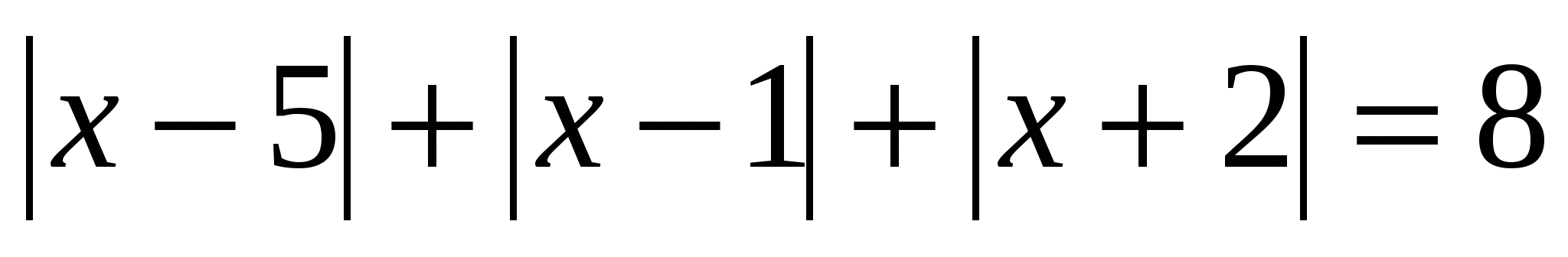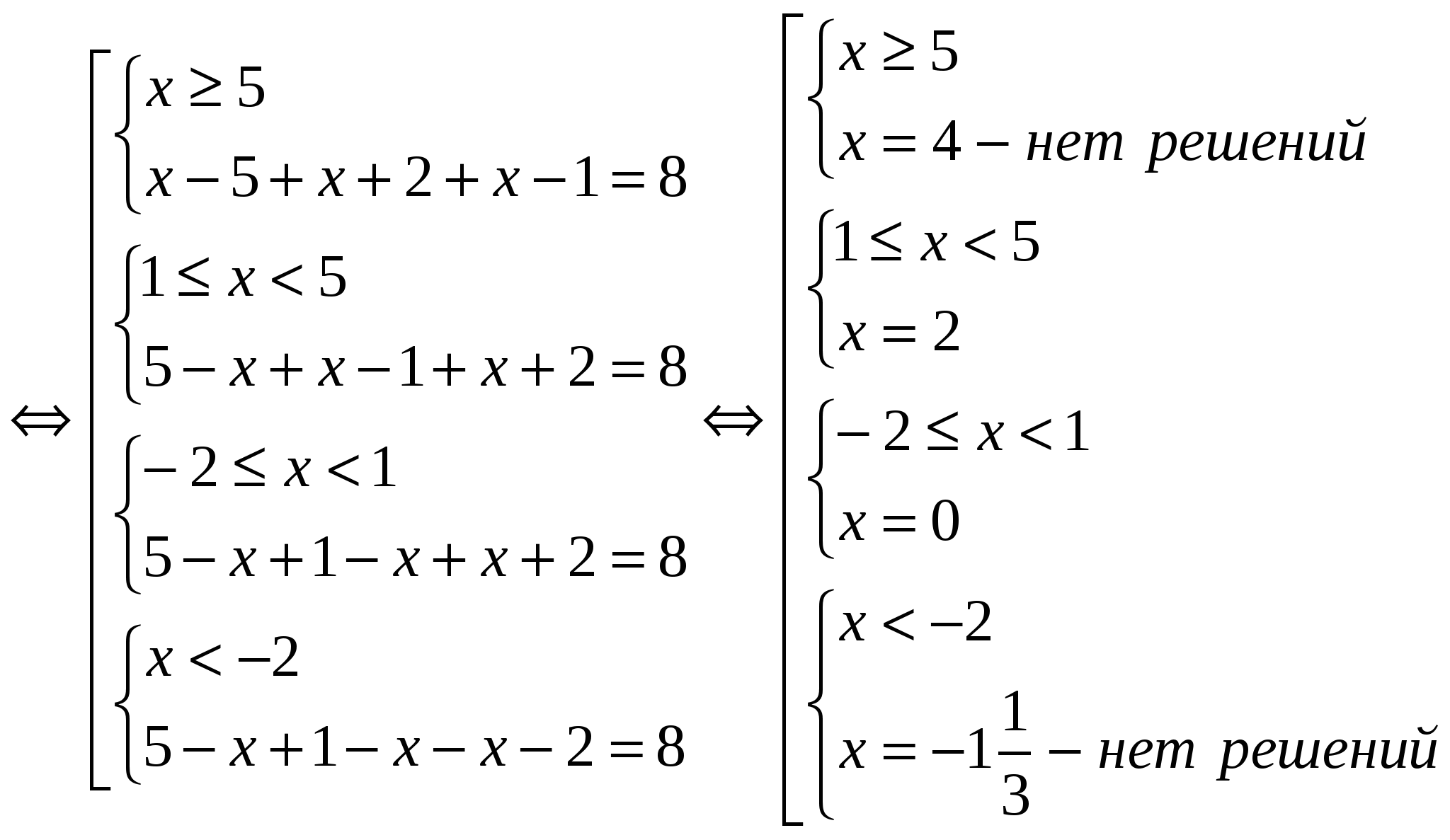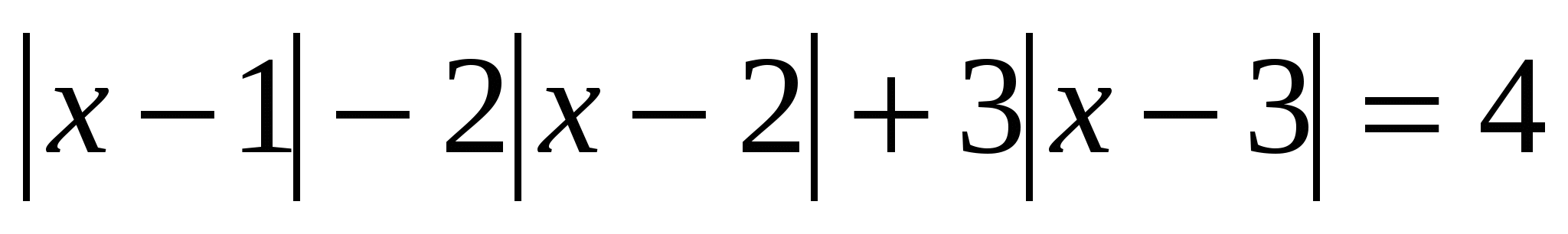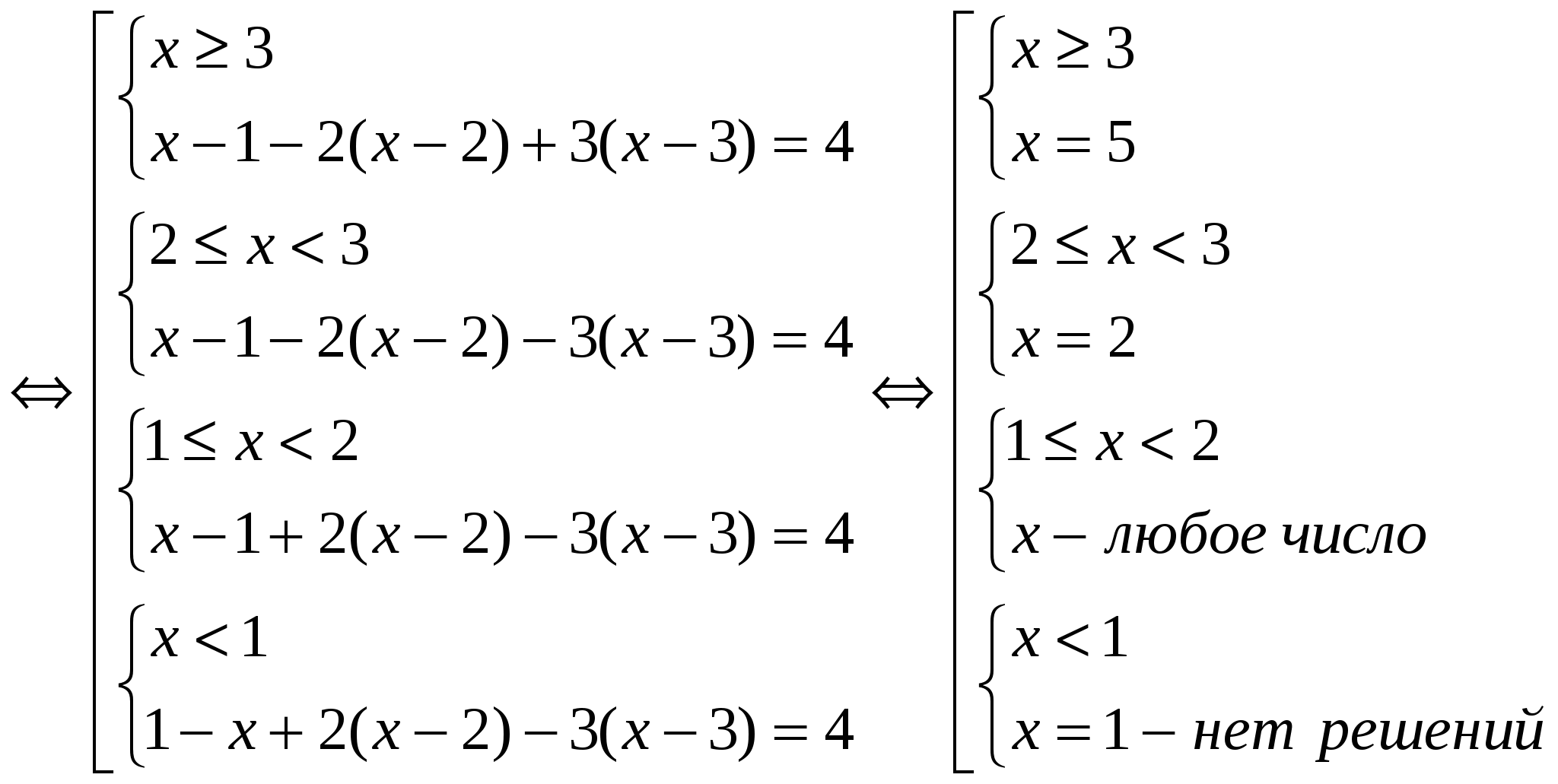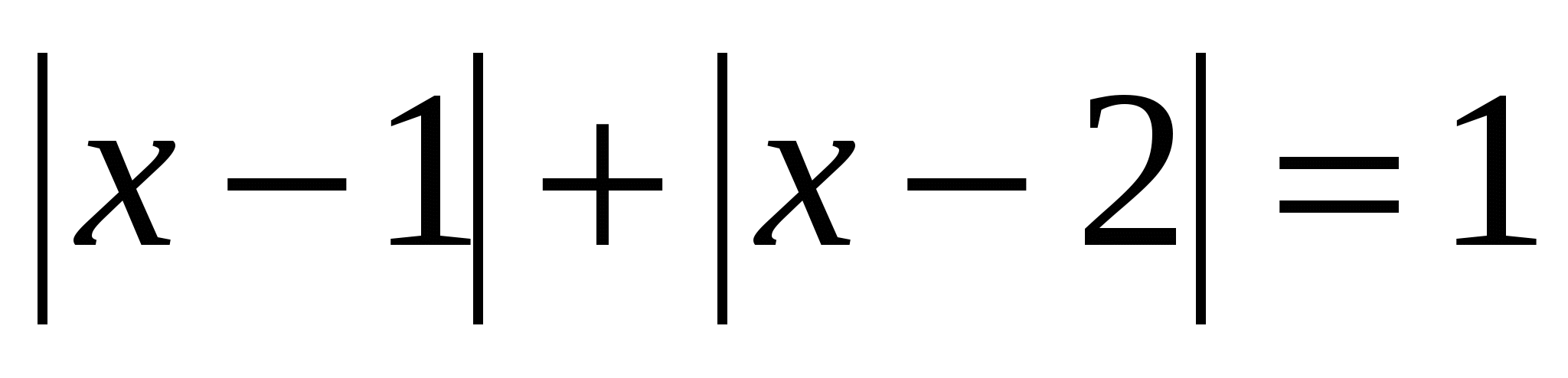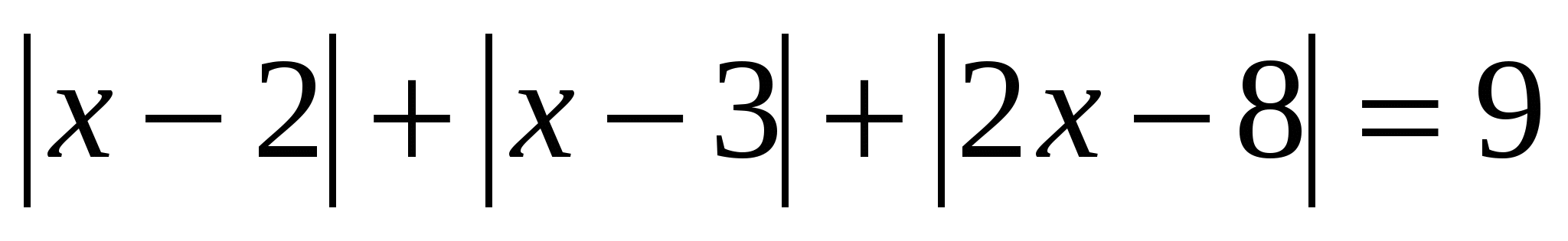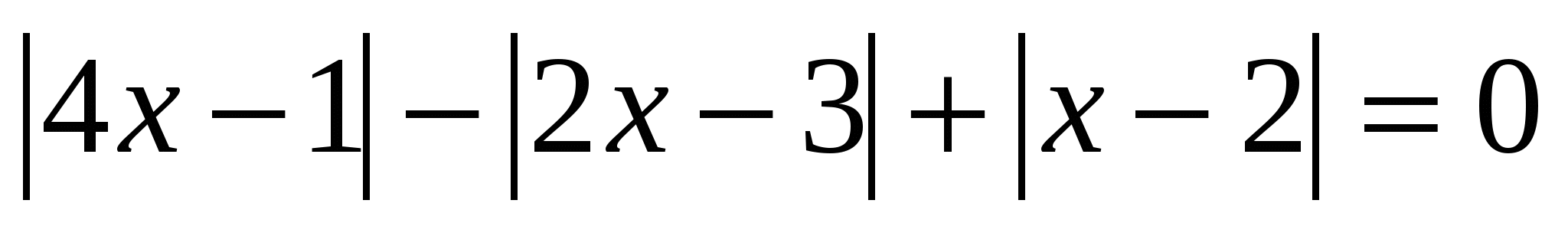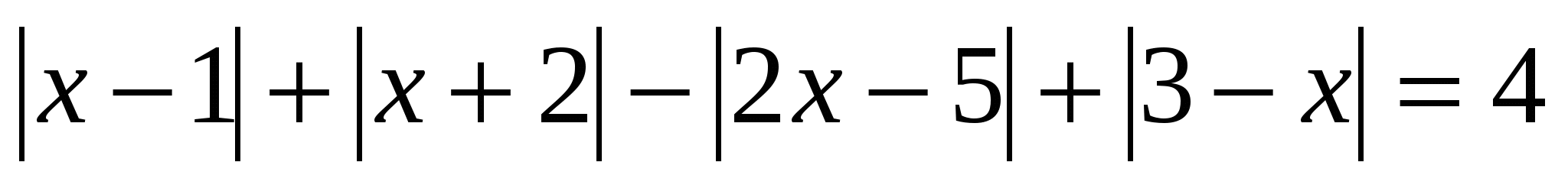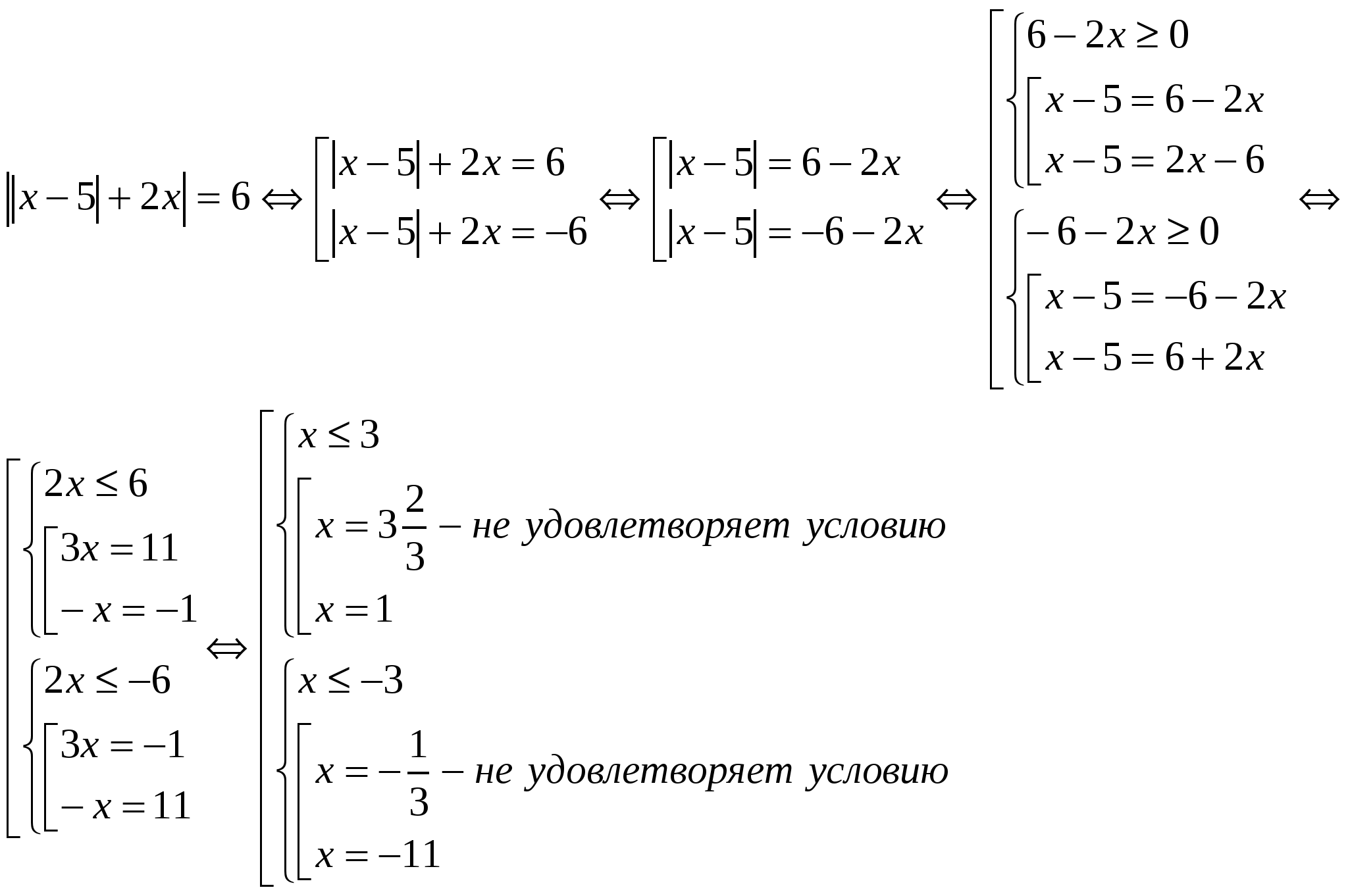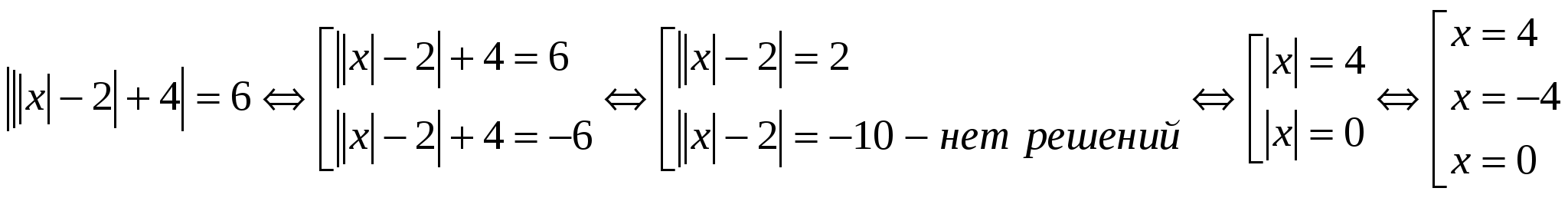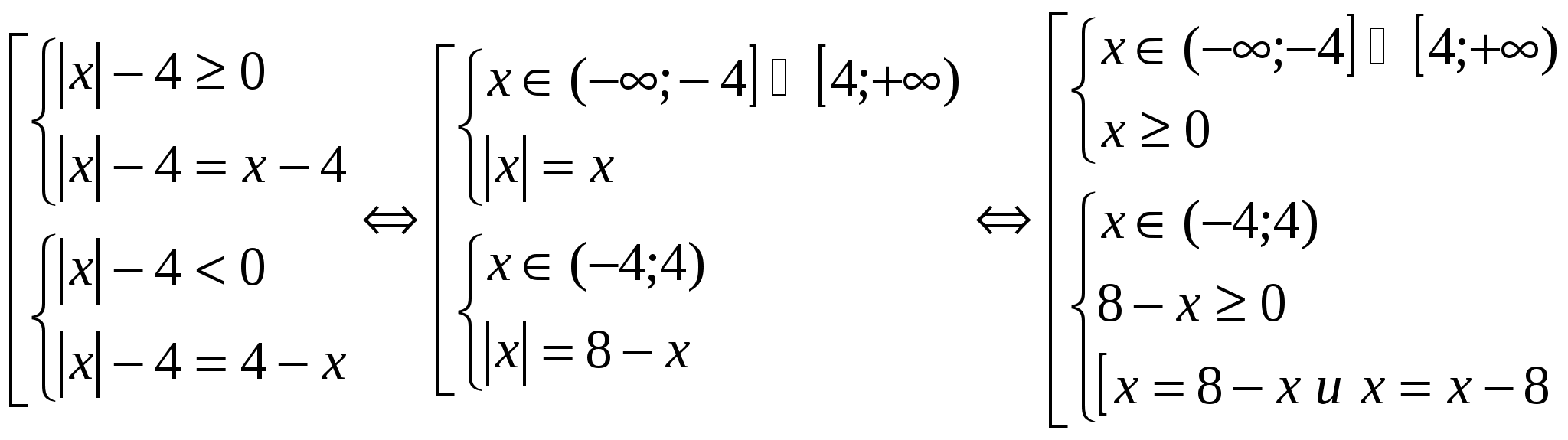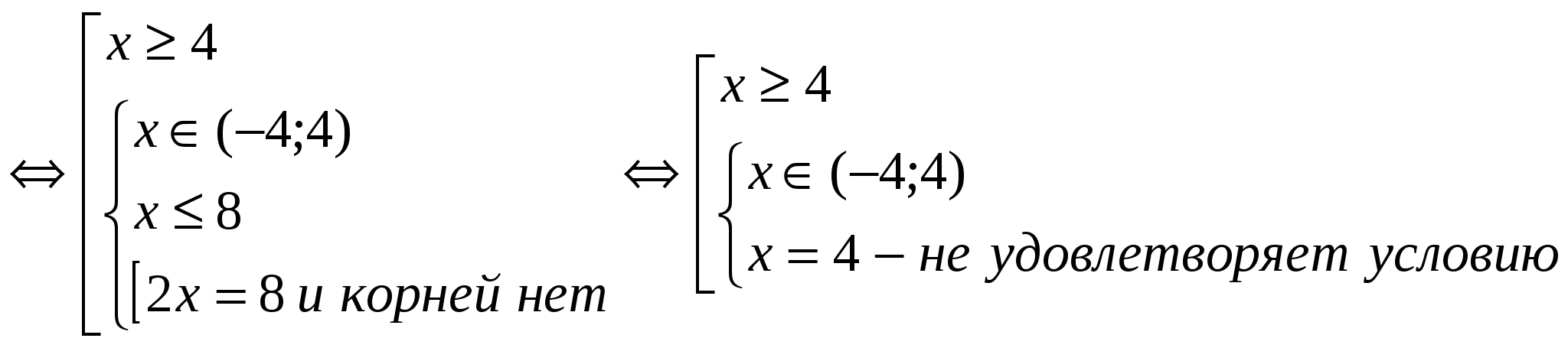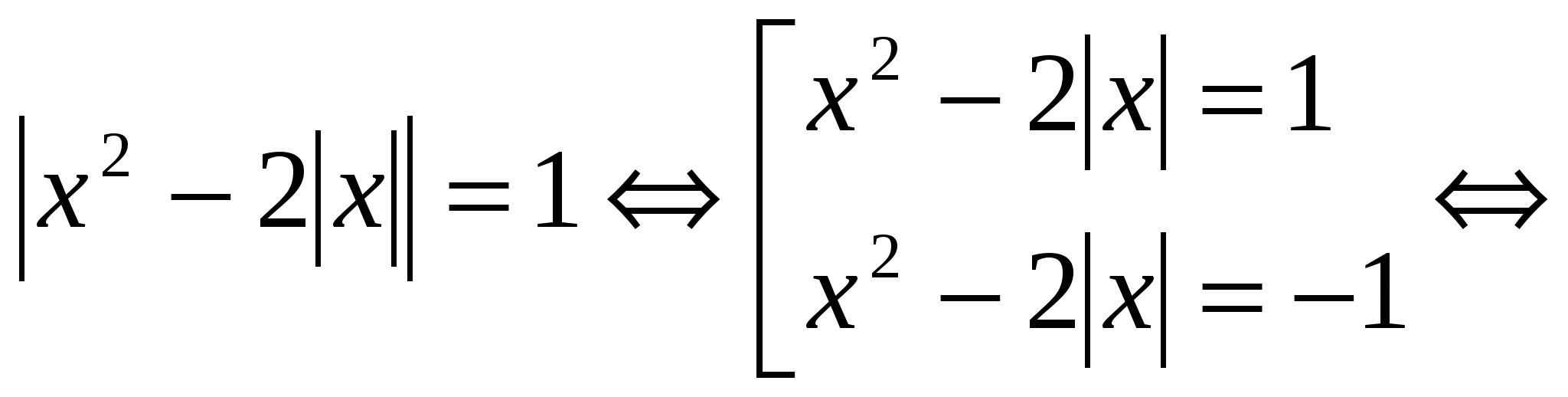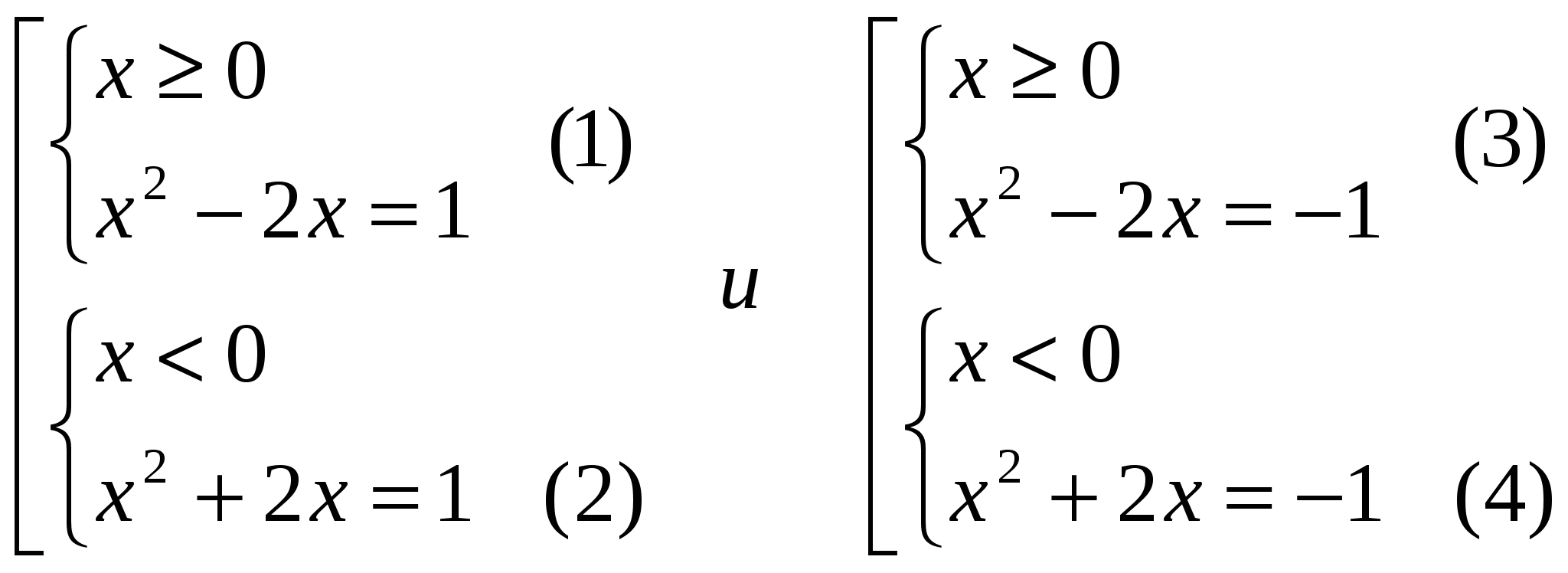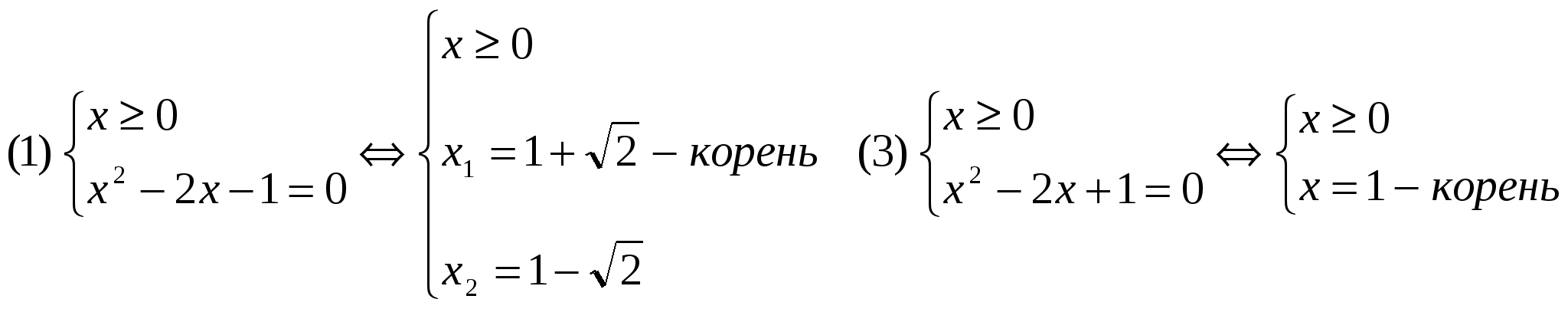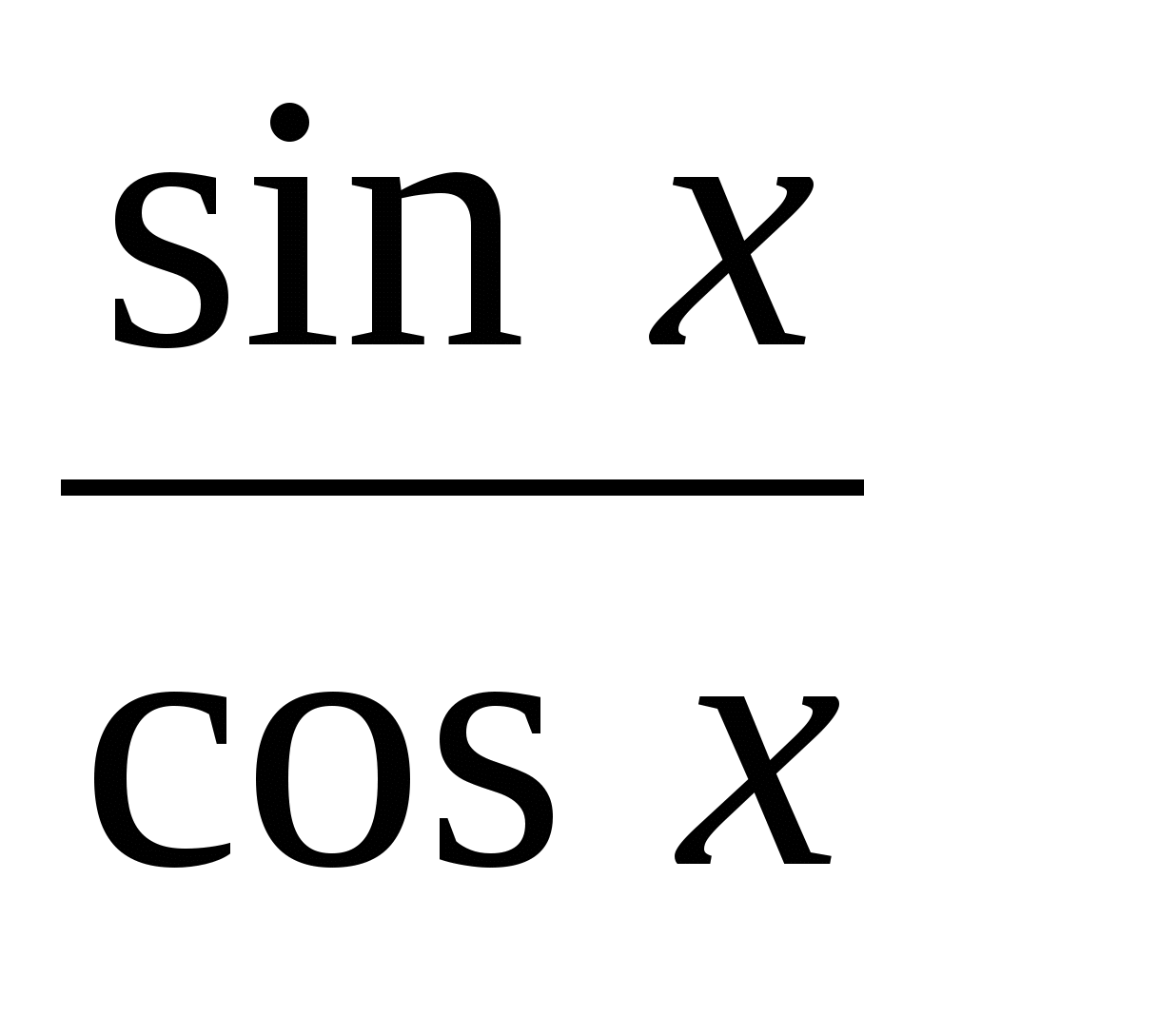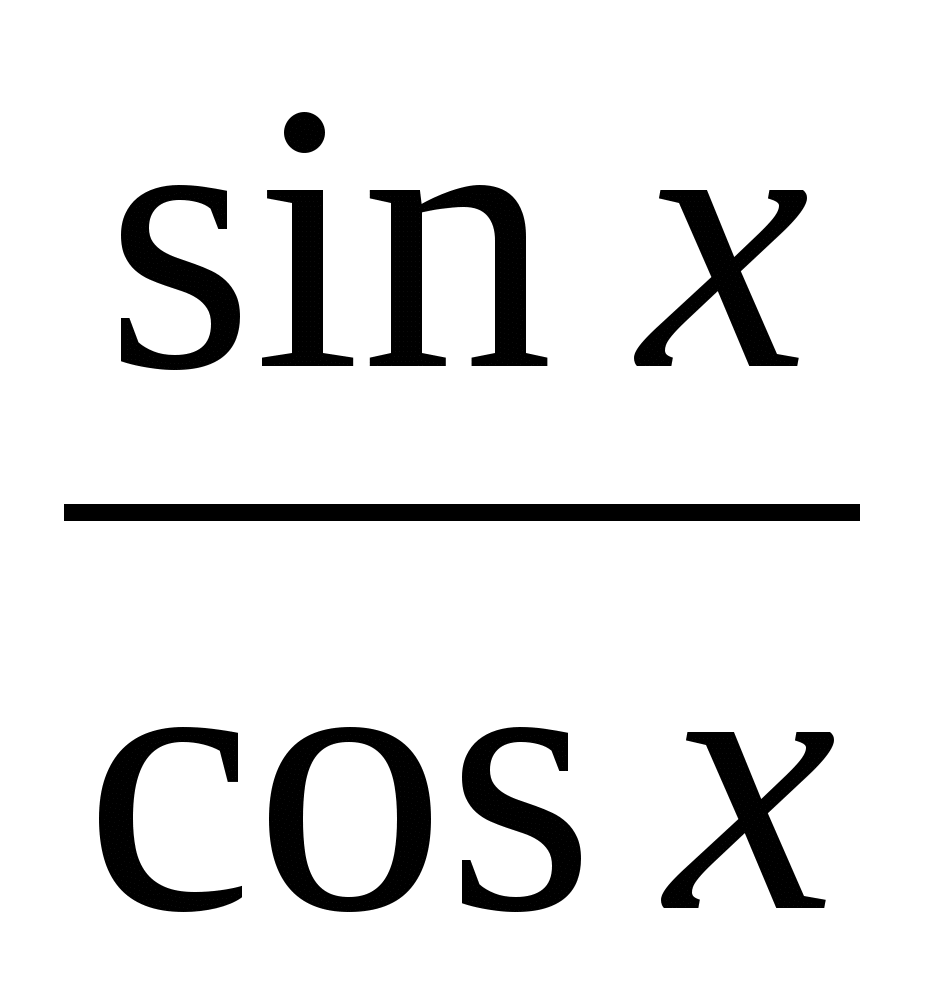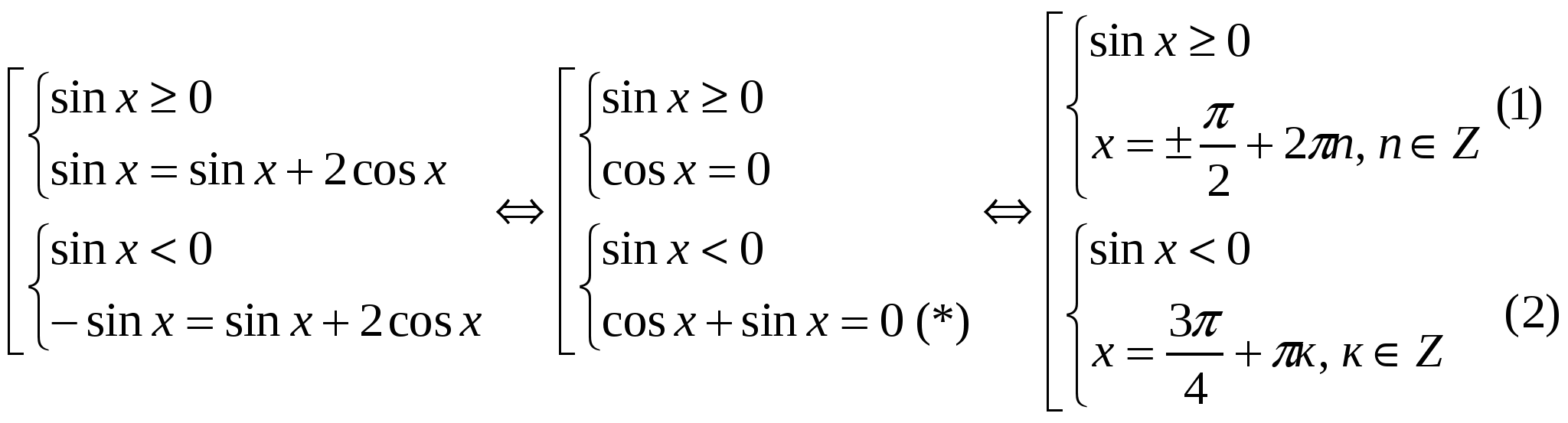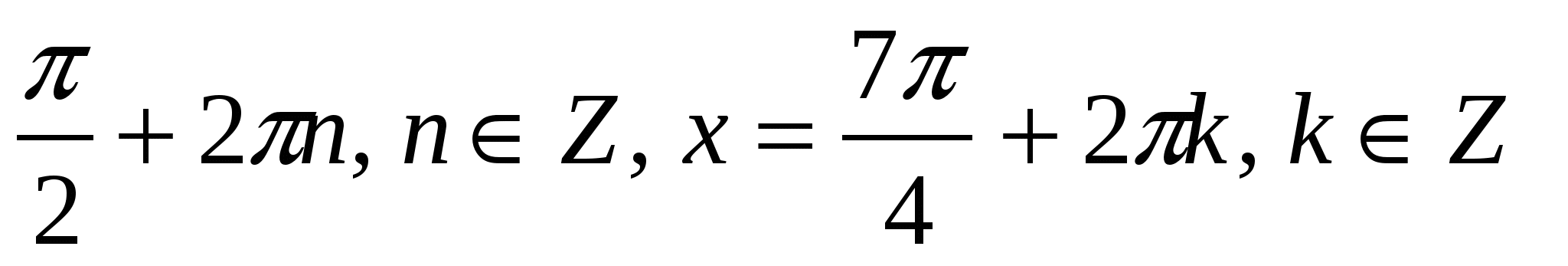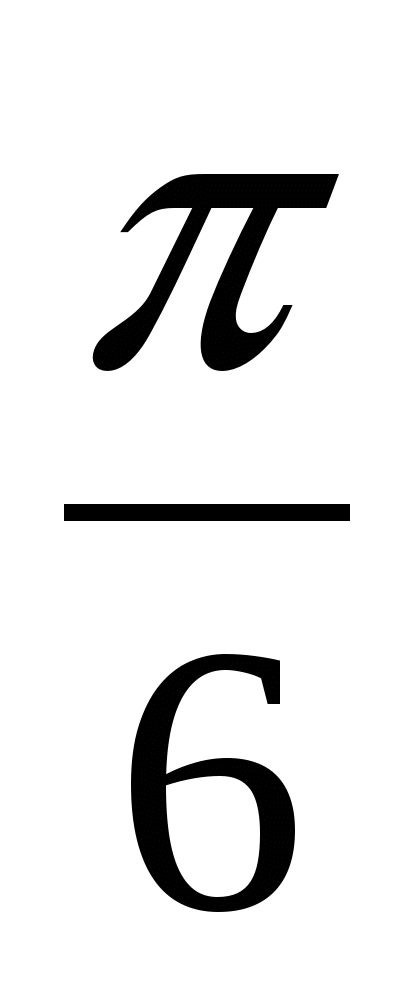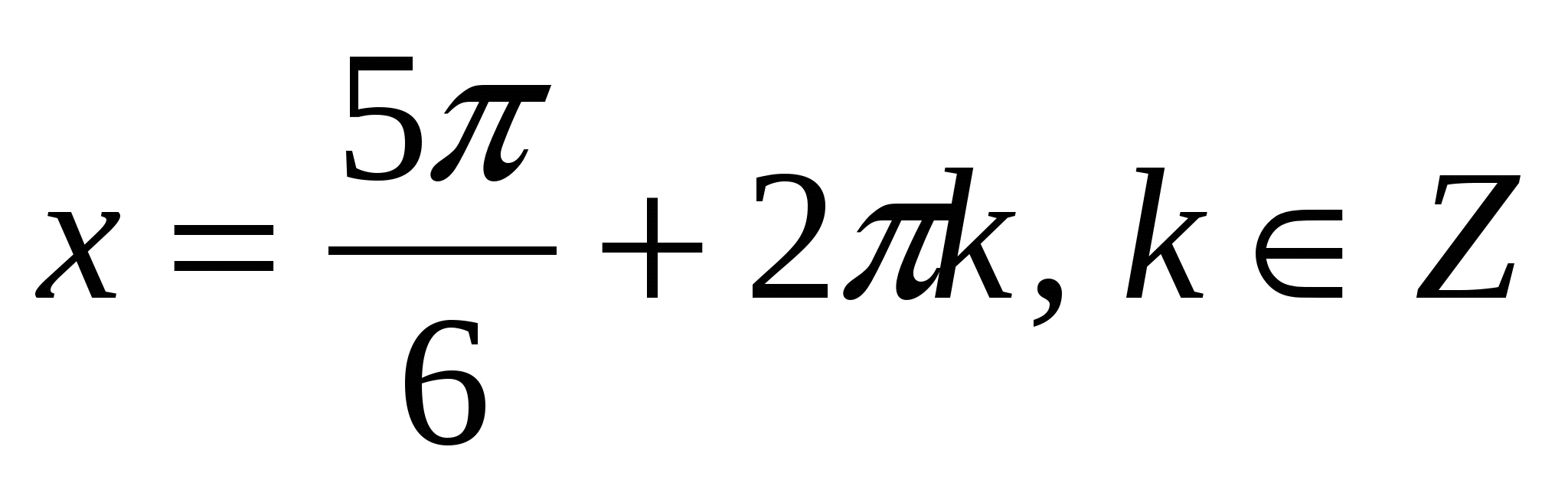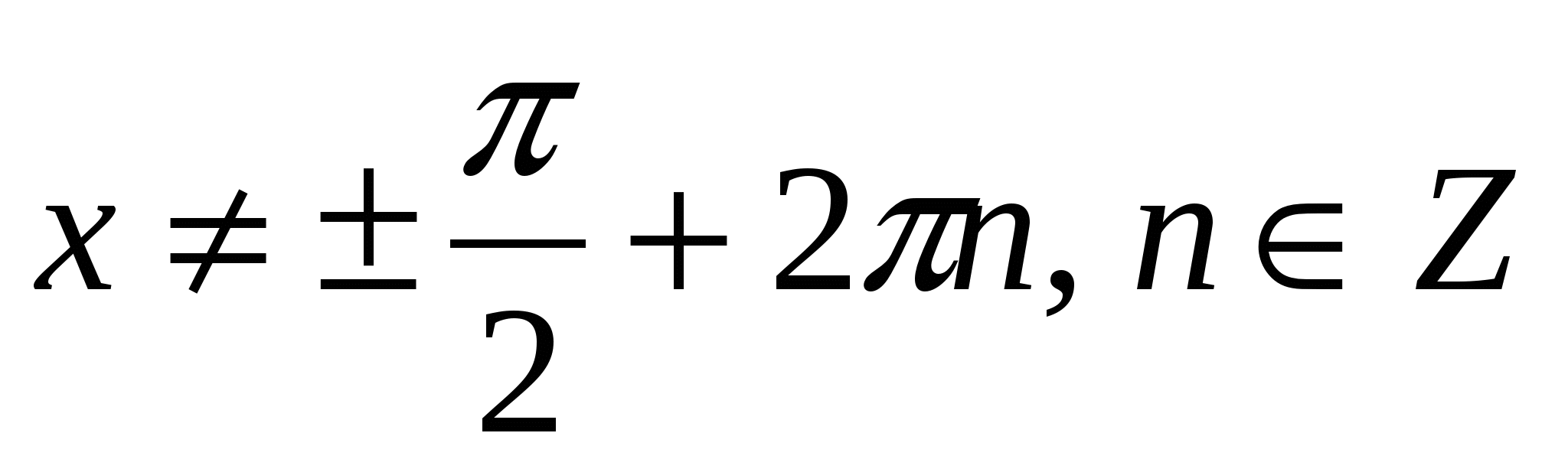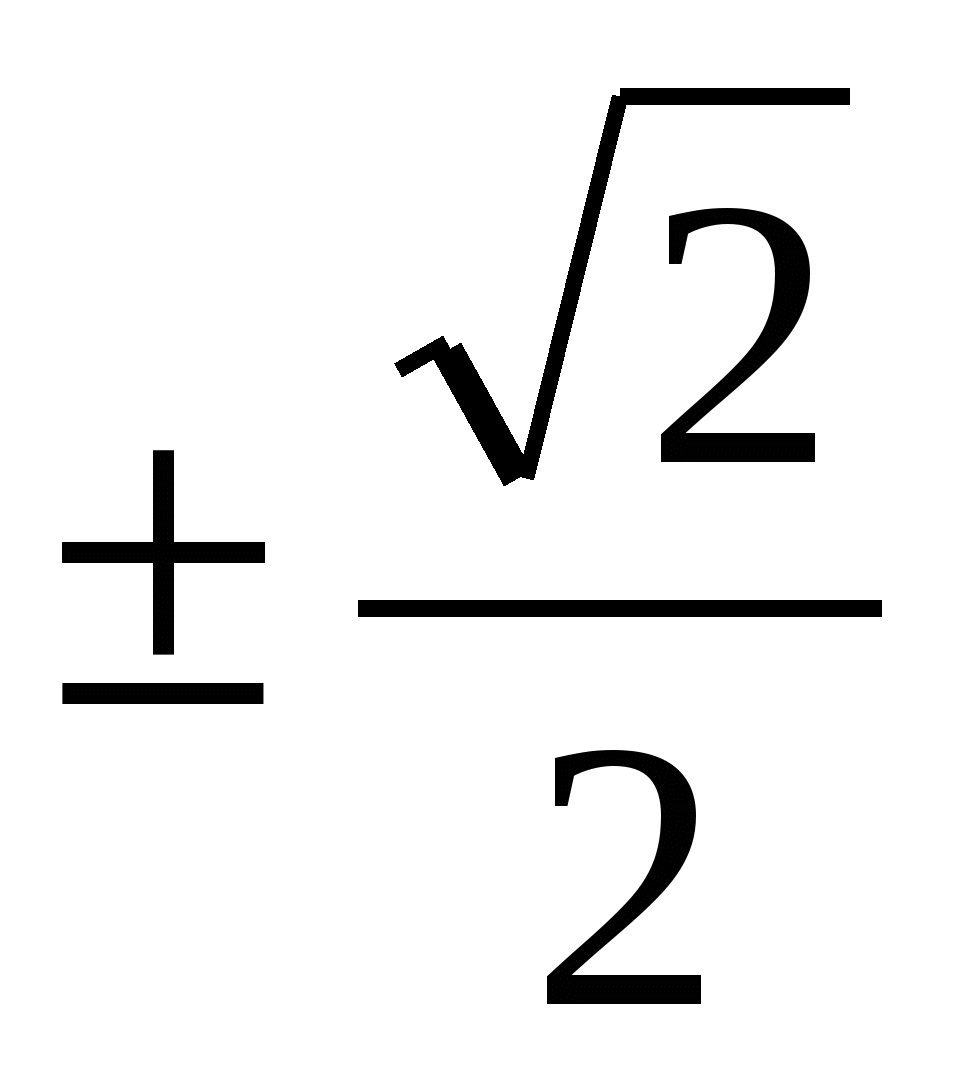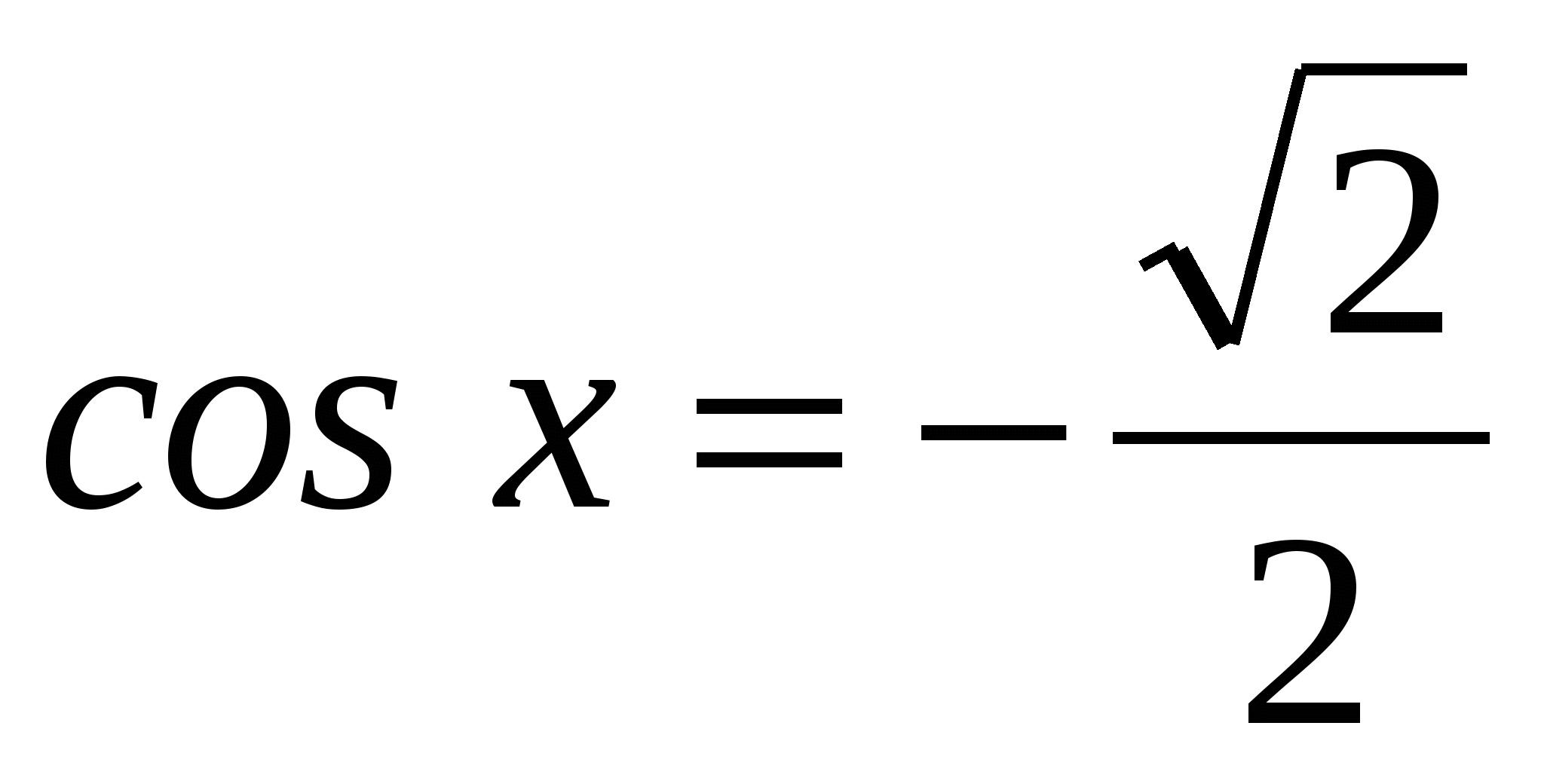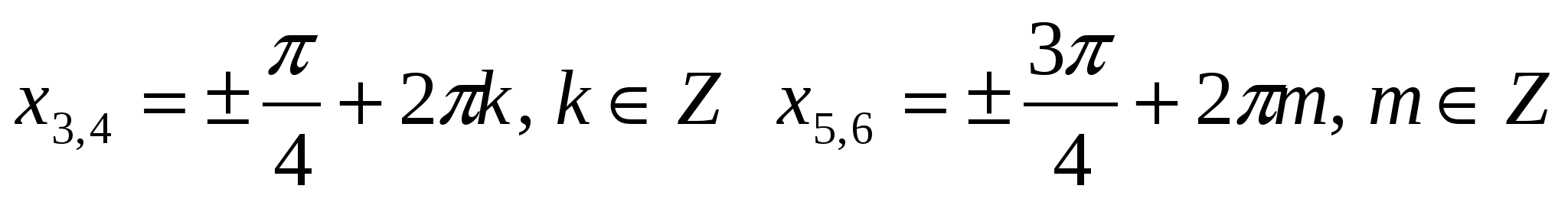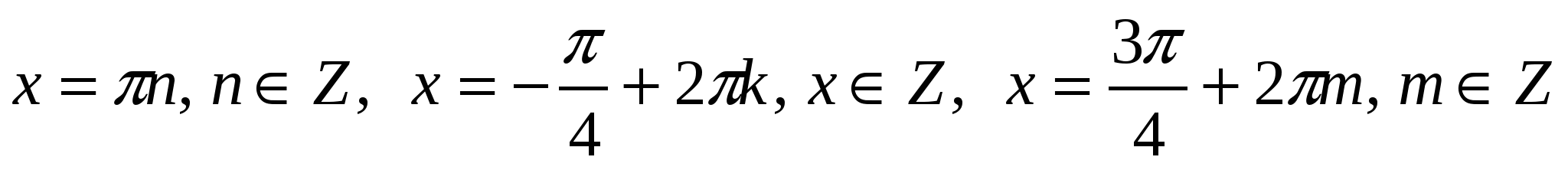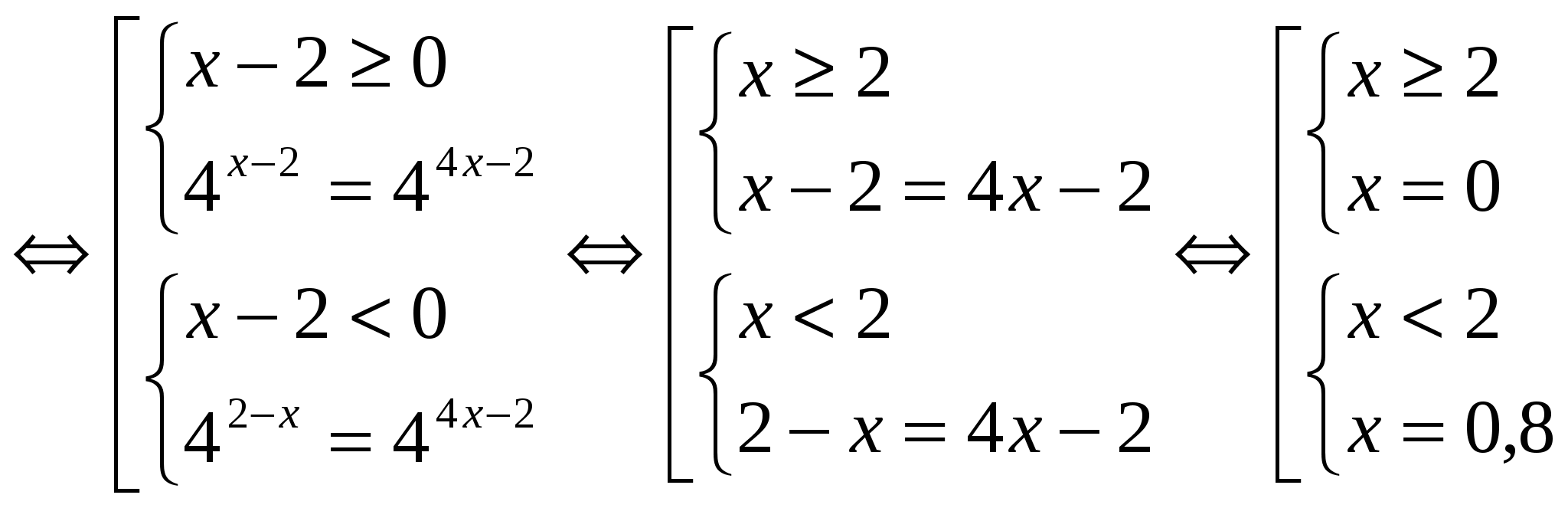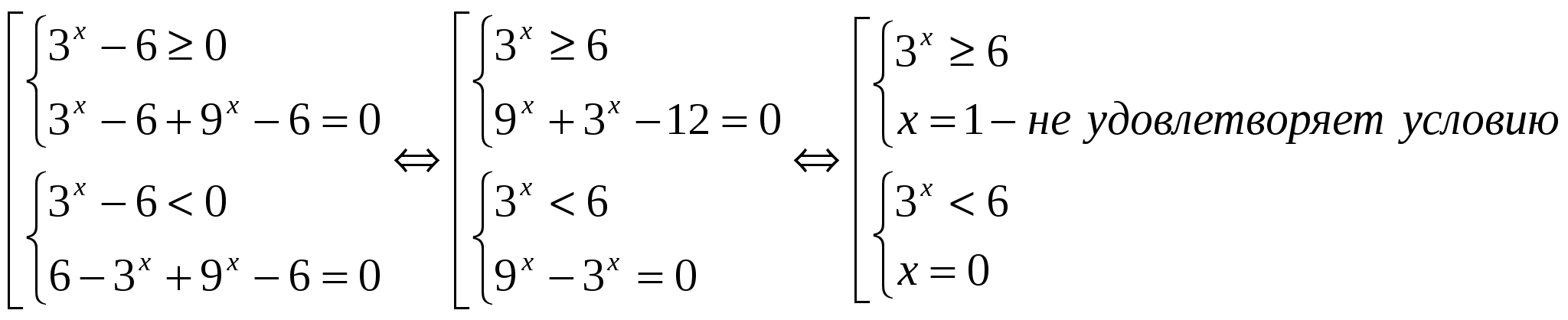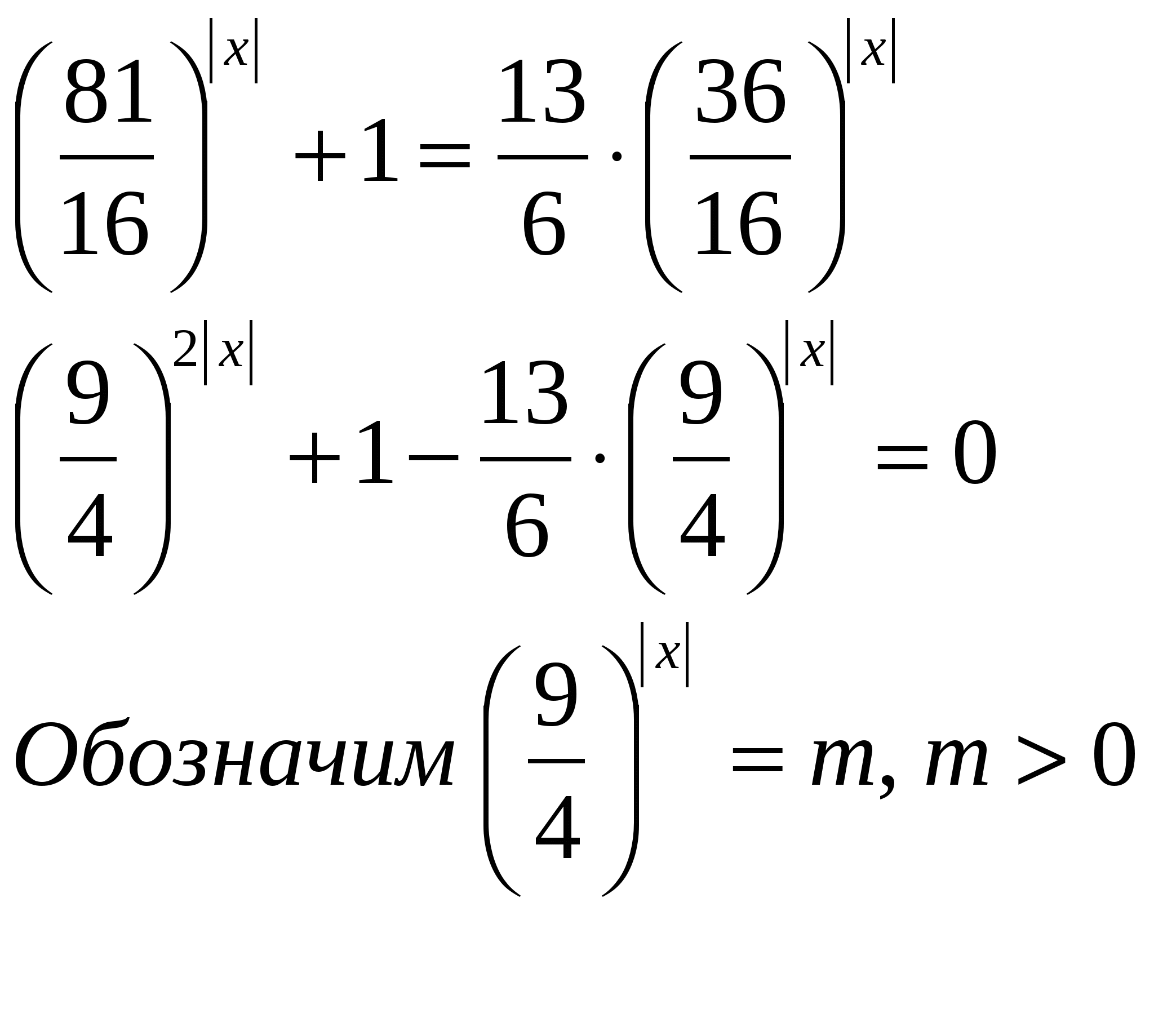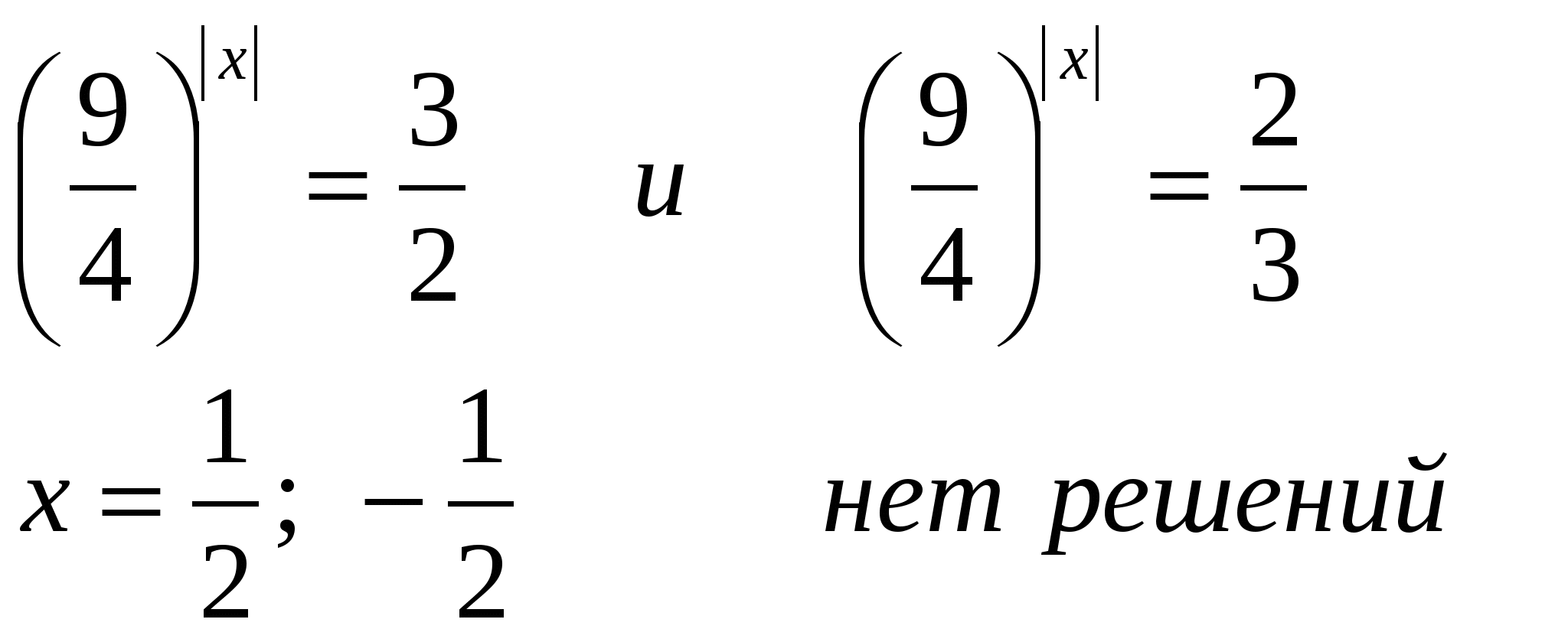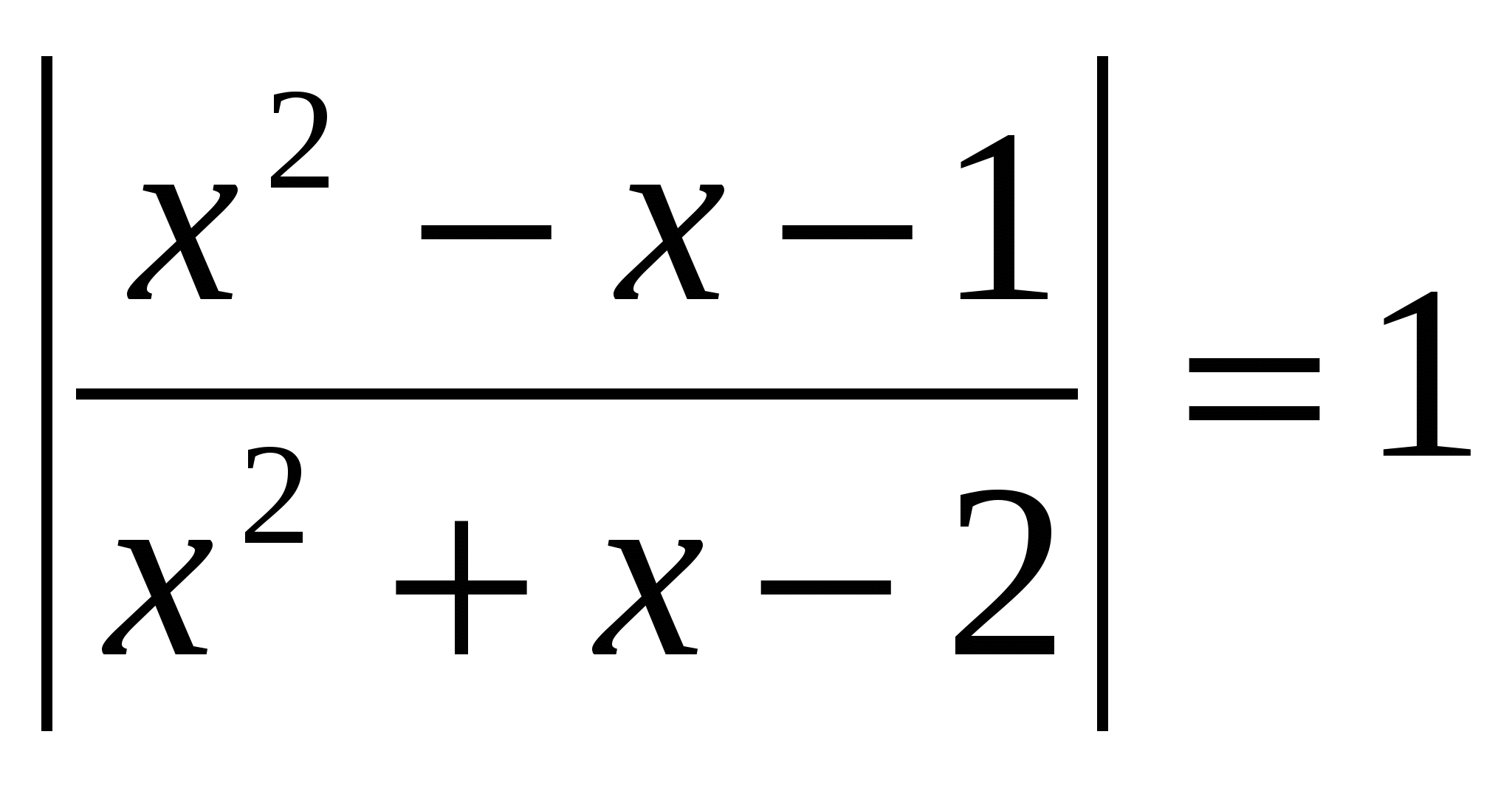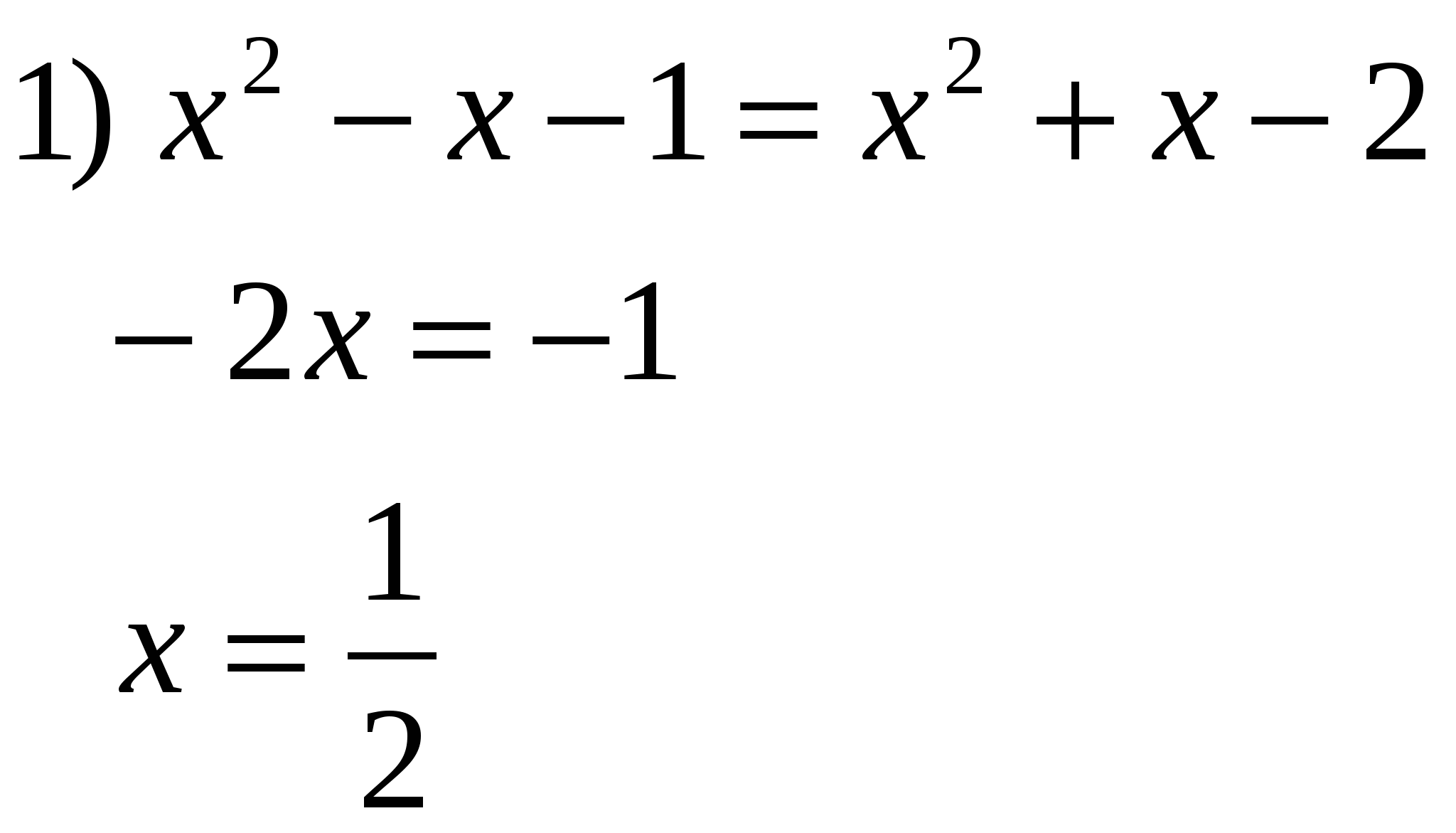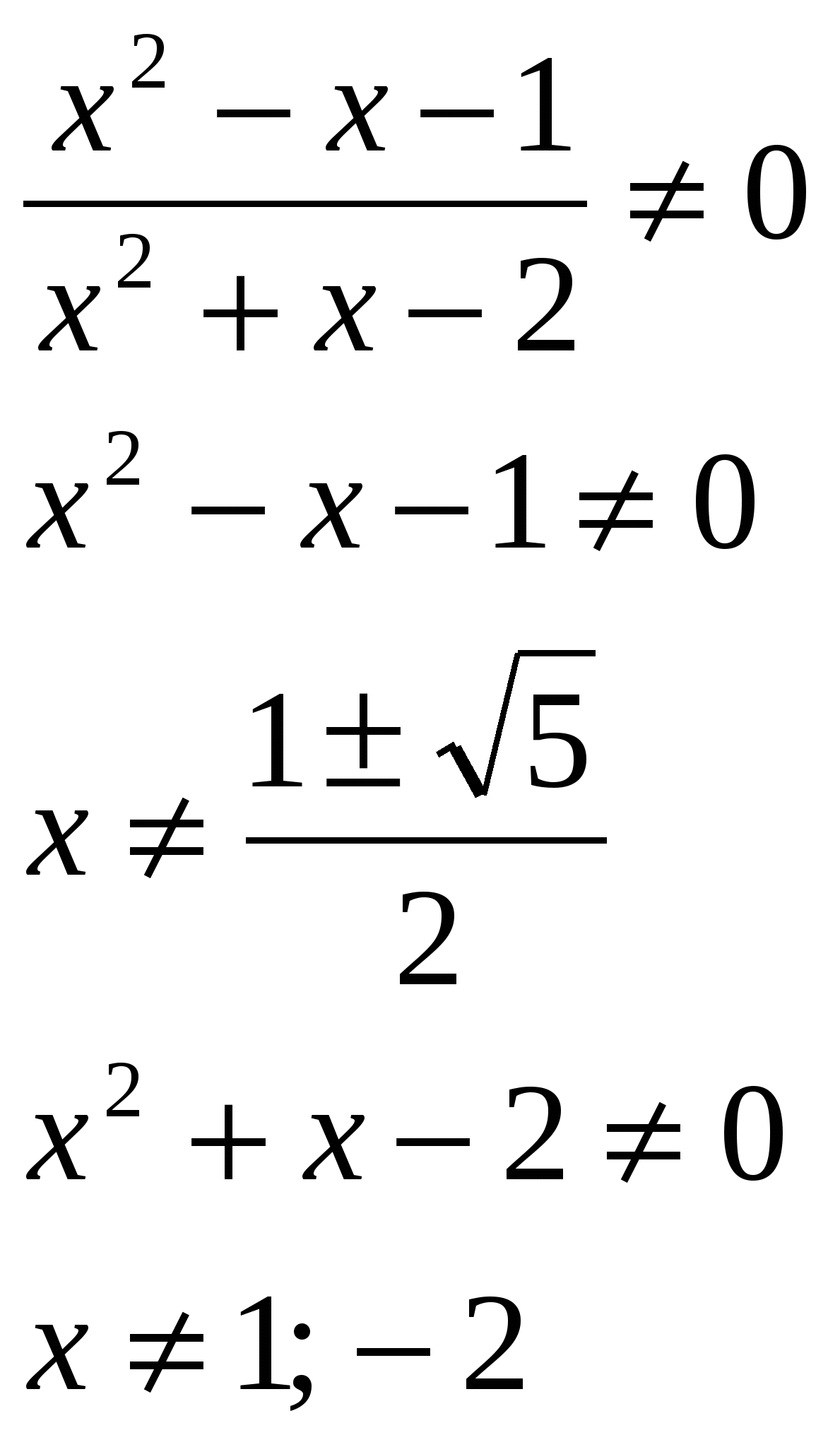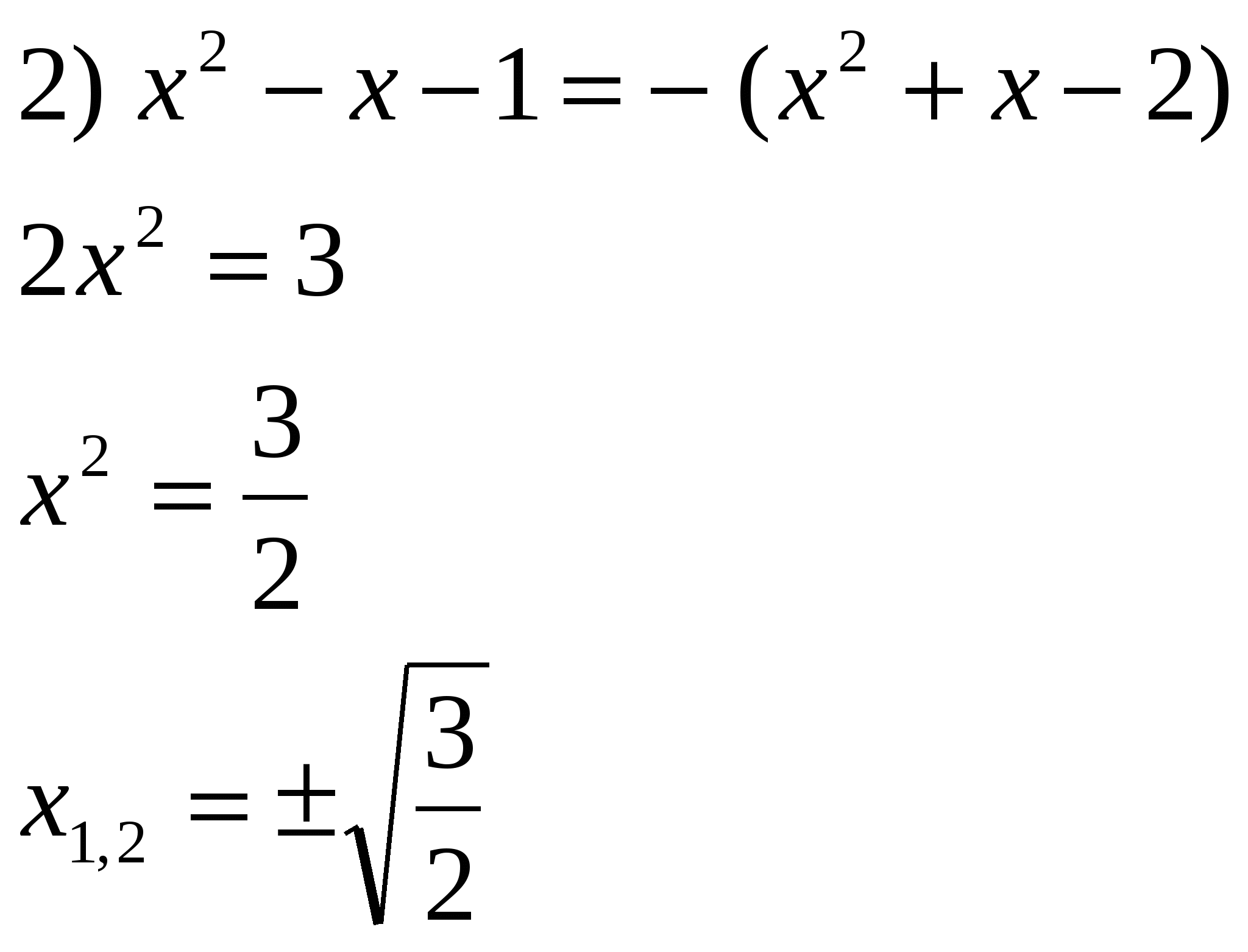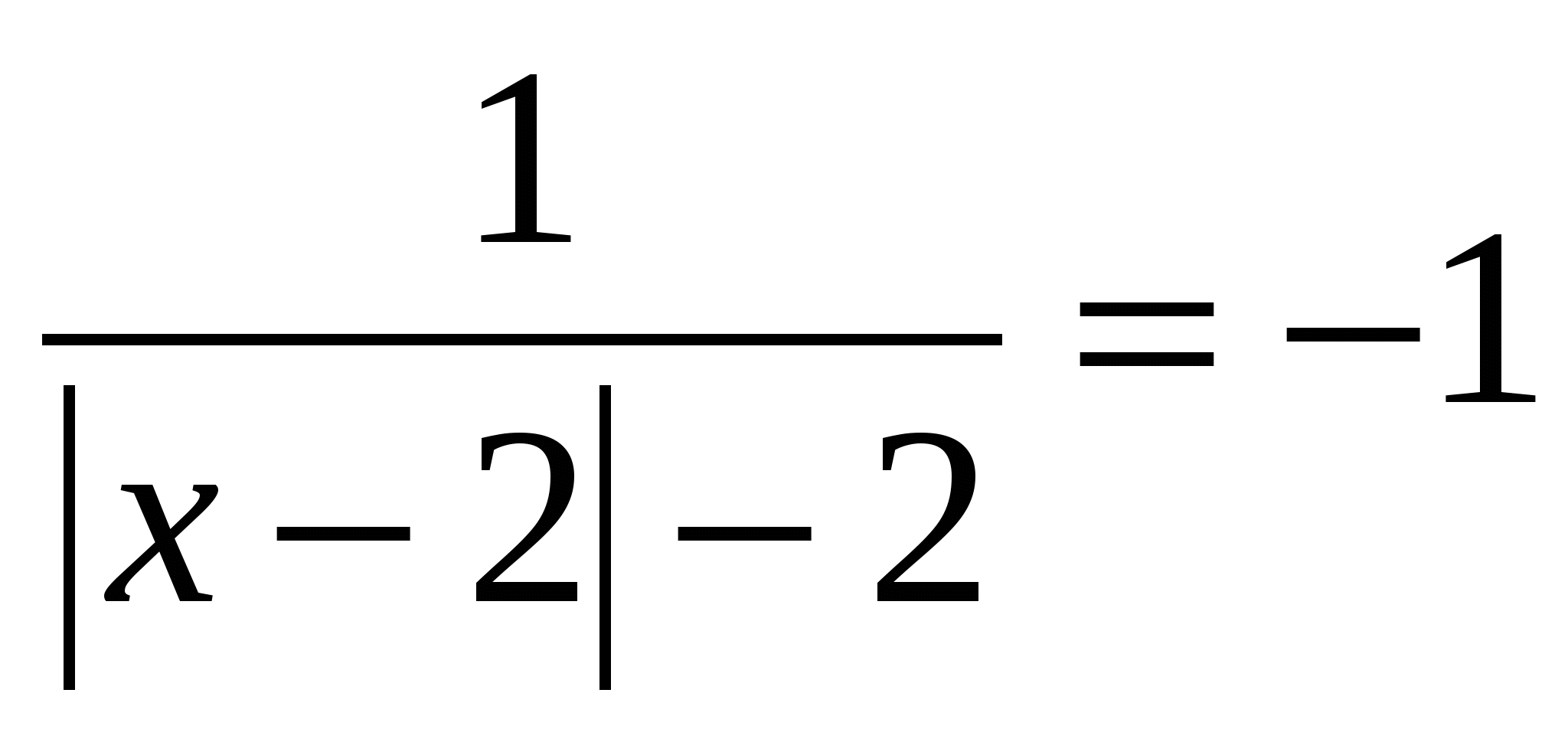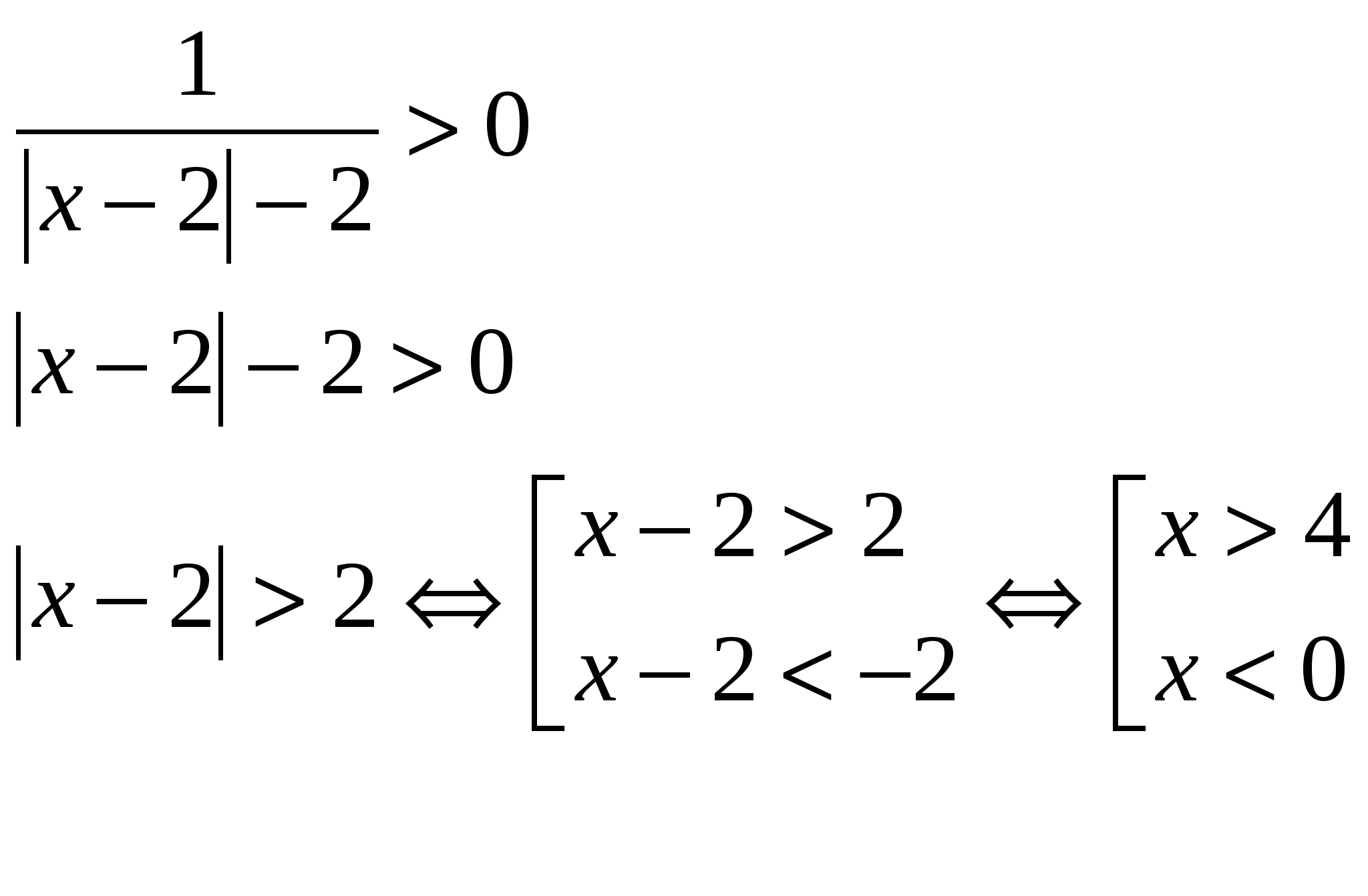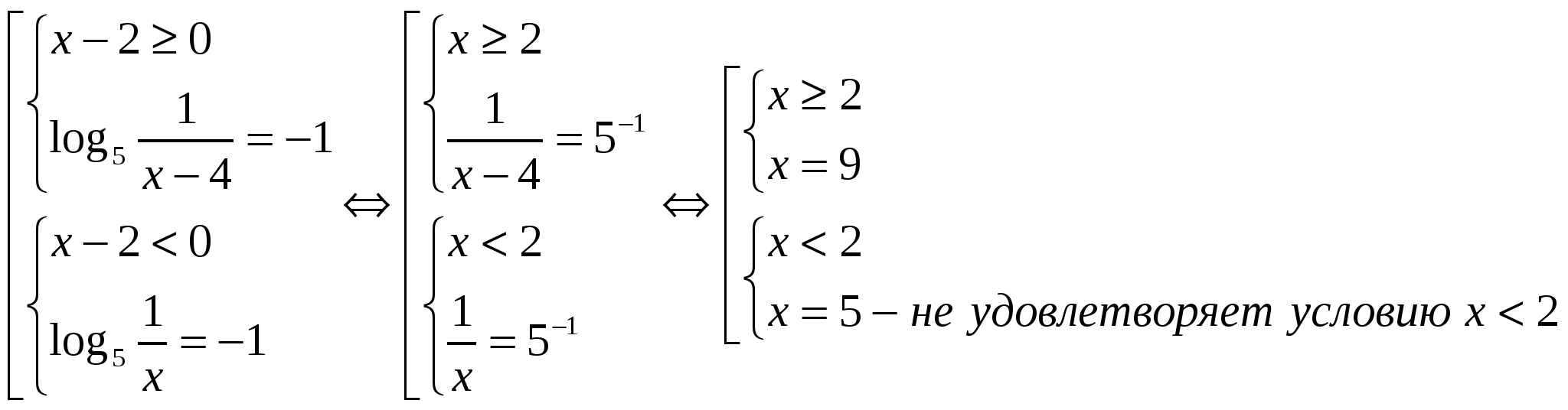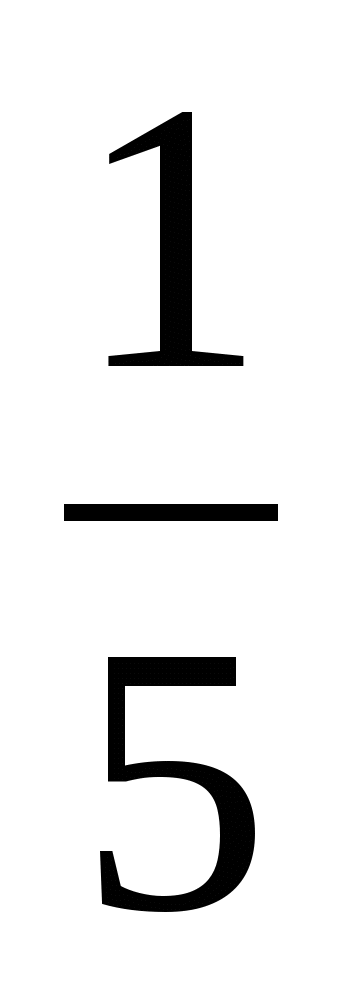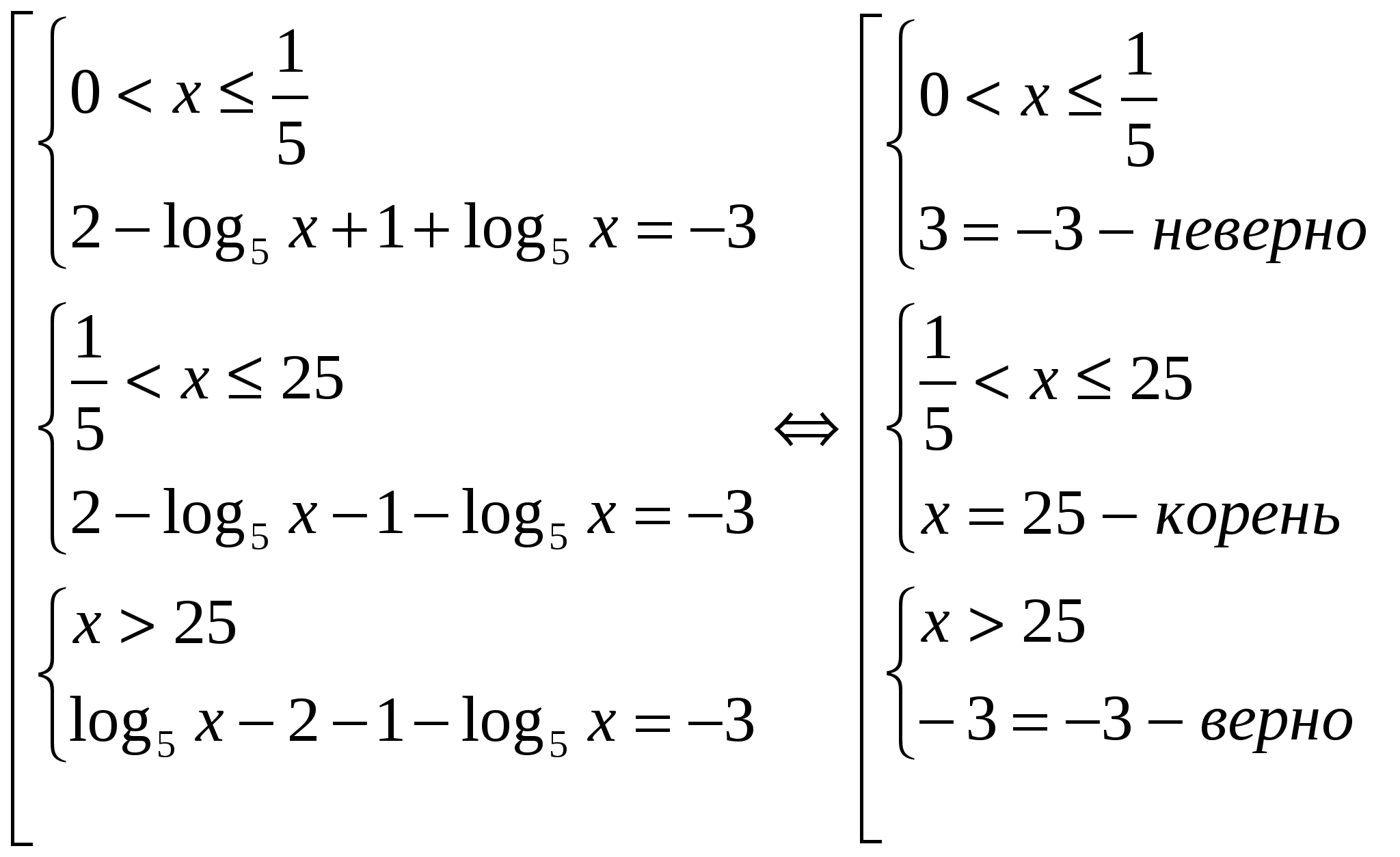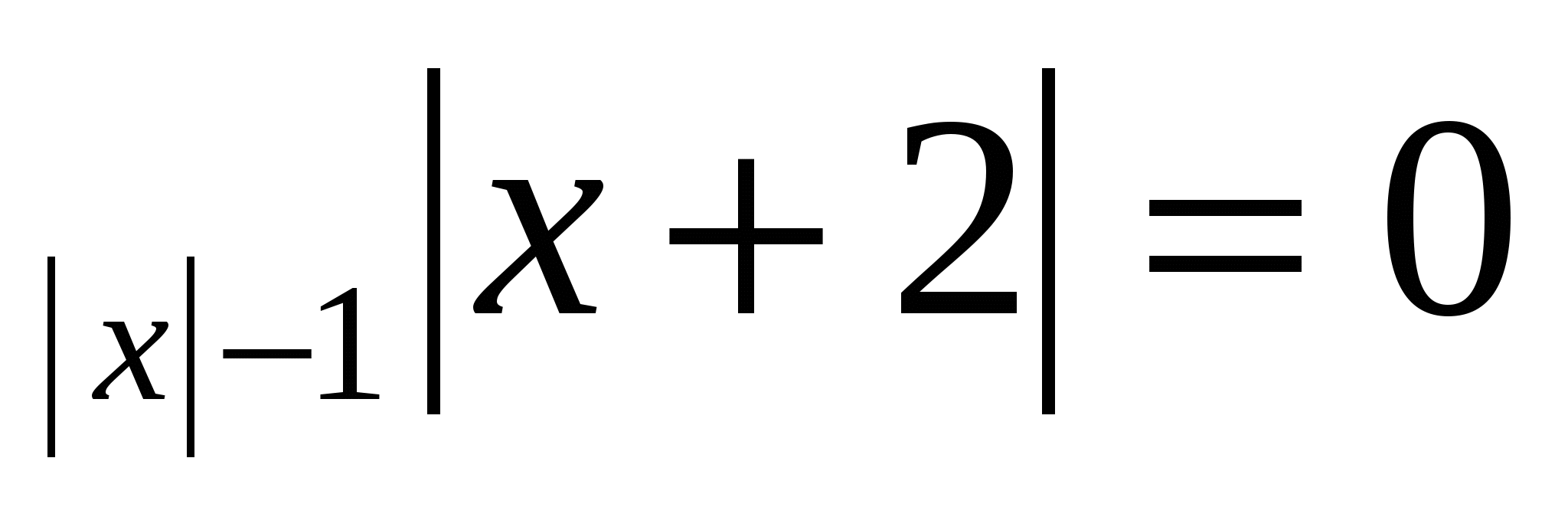Урок по алгебре и началам анализа в 11-м классе «Решение логарифмических неравенств, содержащих знак модуля»

Разделы: Математика

Цели:

1) Научить решать логарифмические неравенства со знаком модуля различными способами.

2) Повторить свойства логарифмической функции и её график.

Оборудование:

3) координатная плоскость.

Целью данного урока является повторение свойств логарифмической функции при решении логарифмических неравенств, содержащих знак модуля и изучение различных способов решения таких неравенств. Решение названных неравенств относится к задачам повышенной сложности.

Теоретическое обоснование различных способов решения неравенств, содержащих знак модуля, учащиеся изучили самостоятельно в творческих группах. На уроке представители групп применяют изученную теорию к решению неравенства |3 – log₂x| 1), значит,

logx 3 logx log8 0 logx>1 logx > log2 x > 2.

Общее решение x є (2;8]

Рассмотрим 2 случай решения.

| а | =

Если 3 — logx logx > 3 logx > log8 x > 8.

При выполнении этого условия данное неравенство примет вид:

— 3 + logx logx logx 0 | log₂x — 3 | 1).

2 0, то |x| — в в

Решение |3 — log₂x | — 2 — 5 1 2 6.02.2008

Алгебра

План урока:

Задание. Укажите корень логарифмического уравнения

Задание. Решите урав-ние

В чуть более сложных случаях под знаком логарифма может стоять не сама переменная х, а выражение с переменной. То есть урав-ние имеет вид

Задание. Найдите решение логарифмического уравнения

Задание. Решите урав-ние

Задание. Решите урав-ние

Получили показательное уравнение. Показатели степеней можно приравнять, если равны их основания:

Уравнения вида log_af(x) = log_ag(x)

Порою логарифм стоит в обеих частях равенства, то есть и слева, и справа от знака «равно». Если основания логарифмов совпадают, то должны совпадать и аргументы логарифмов.

Задание. Решите урав-ние

Задание. Найдите корень урав-ния

Ситуация несколько усложняется в том случае, когда, под знаком логарифма в обоих частях равенства стоят выражения с переменными, то есть оно имеет вид

С одной стороны, очевидно, что должно выполняться равенство f(x) = g(x). Но этого мало, ведь под знаком логарифма не должно стоять отрицательное число. Поэтому после получения корней следует подставить их в урав-ние и убедиться, что они не являются посторонними корнями.

Задание. Решите урав-ние

Получили квадратное уравнение, которое решаем с помощью дискриминанта:

Получили два корня, (– 3) и 4. Однако теперь подставим их в исходное урав-ние и посмотрим, что у нас получится. При х = – 3 имеем:

Это верное равенство, поэтому х = – 3 действительно является корнем урав-ния. Теперь проверяем х = 4:

Хотя выражения и справа, и слева одинаковы, равенство верным считать нельзя, ведь выражение log₃ (– 1) не имеет смысла! Действительно, нельзя вычислять логарифм от отрицательного числа. Поэтому корень х = 4 оказывается посторонним, и у нас остается только один настоящий корень – число (– 3).

Уравнения, требующие предварительных преобразований

Естественно, не всегда в обоих частях логарифмических уравнений и неравенств стоят только логарифмы с совпадающими основаниями. Часто требуется выполнить некоторые предварительные преобразования, чтобы привести урав-ние к виду log_af(x) = log_ag(x).

Задание. Решите урав-ние

с помощью которой любой множитель можно внести под знак логарифма. Сделаем это и в нашем случае:

Теперь в обеих частях равенства не стоит ничего, кроме логарифмов с одинаковыми основаниями. Поэтому мы можем приравнять их аргументы:

Задание. Решите урав-ние

Снова проверяем каждый из корней, подставляя его в исходное ур-ние. Прих = –1 получаем

Задание. Решите урав-ние

Решение. В правой части снова стоит сумма, но на этот раз не логарифмов. Однако число 1 можно представить как log₅ 5. Тогда урав-ние можно преобразовать:

Задание. Решите урав-ние

Решение. Данный пример похож на простейшее логарифмическое уравнение, однако переменная находится в основании логарифма, а не в аргументе. По определению логарифма мы можем записать, что

Первый вариант придется отбросить, так как основание логарифма, (а в данном случае это выражение х – 5) не может быть отрицательным числом. Получается, что

Задание. Решите урав-ние

Решение. Здесь ситуация осложняется тем, что основания логарифмов разные. Поэтому один из них необходимо привести к новому основанию. Попробуем привести log₂₅x 4 к основанию 5, используя известную нам формулу

Мы добились того, что у логарифмов одинаковые основания, а потому мы можем приравнять их аргументы:

Логарифмические уравнения с заменой переменных

Иногда приходится делать некоторые замены, чтобы уравнение приняло более привычный вид.

Задание. Решите уравнение методом замены переменной

Задание. Найдите решение уравнения методом замены переменной

Решение. Для начала напомним, что символ lg означает десятичный логарифм. Отдельно знаменатель дроби в правой части:

Логарифмирование уравнений

Ясно, что если от равных величин взять логарифмы по одному и тому же основанию, то тогда эти логарифмы окажутся также равными. Если подобный прием применяют при решении урав-ния, то, говорят, что производится логарифмирование уравнения. Иногда оно позволяет решить некоторые особо сложные примеры.

Задание. Укажите корни урав-ния

Здесь переменная величина находится одновременно и в основании степени, и в ее показателе. Возьмем от правой и левой части урав-ния логарифм по основанию 5:

Возвращаемся от переменной t к переменной х:

Переход от логарифмических неравенств к нелогарифмическим

Рассмотрим график логарифмической функции у = log_ax при условии а > 1. Она является возрастающей функцией. Если на оси Ох отложить два числа tи s так, чтобы t располагалось левее s (то есть t 1). Но это не совсем так. Дело в том, что надо учесть ещё и тот факт, что под знаком логарифма может стоять исключительно положительное число. Получается, что от простейшего логарифмического неравенства

Естественно, вместо величин t и s могут стоять как числа, так и выражения с переменными.

Задание. Найдите решение логарифмического неравенства

Ответ можно оставить и в такой форме, однако всё же принято записывать его в виде промежутка. Очевидно, что нерав-во 0 log_as:

Но, снова-таки, мы должны учесть, числа t может быть лишь положительным (тогда s, которое больше t, автоматически также окажется положительным). Получается, что при 0 log_a s можно перейти к двойному нерав-ву 0 2 – 45х + 200 имеет решение

Однако в системе (5) есть ещё два неравенства, х > 0 и 45 >x. Их решениями являются промежутки (0; + ∞) и (– ∞; 45). Чтобы определить решение всей системы, отметим на одной прямой решения каждого отдельного нерав-ва и найдем область их пересечения:

Видно, что решениями нерав-ва будут являться промежутки (0; 5) и (40; 45), на которых справедливы все три нерав-ва, входящих в систему (5).

Содержание:

Пояснительная записка

Глава 1. Введение

Раздел 1. Определение абсолютной величины

Раздел 2. Основные свойства

Раздел 3. Геометрическая интерпретация понятия модуля числа

Раздел 4. График функции у = |х|

Раздел 5. Условные обозначения

Глава 2. Решение уравнений, содержащих модуль

Раздел 1.Уравнения вида | F (х)| = m (простейшие)

Раздел 2. Уравнения вида F (|х|) = m

Раздел 3. Уравнения вида | F (х)| = G (х)

Раздел 4. Уравнения вида | F (х)| = ± F (х) (красивейшие)

Раздел 5. Уравнения вида | F (х)| = | G (х)|

Раздел 6. Примеры решения нестандартных уравнений

Раздел 7. Уравнения вида | F (х)| + | G (х)| = 0

Раздел 8. Уравнения вида |а 1 х ± в 1 | ± |а 2 х ± в 2 | ± …|а n х ± в n | = m

Раздел 9. Уравнения, содержащие несколько модулей

Глава 3. Примеры решения различных уравнений с модулем.

Раздел 1. Тригонометрические уравнения

Раздел 2. Показательные уравнения

Раздел 3. Логарифмические уравнения

Раздел 4. Иррациональные уравнения

Раздел 5. Задания повышенной сложности

Ответы к упражнениям

Пояснительная записка.

Понятие абсолютной величины (модуля) действительного числа является одной из существенных его характеристик. Это понятие имеет широкое распространение в различных разделах физико-математических и технических наук. В практике преподавания курса математики в средней школе в соответствии с Программой МО РФ понятие «абсолютная величина числа» встречается неоднократно: в 6 – м классе вводиться определение модуля, его геометрический смысл; в 8 – м классе формируется понятие абсолютной погрешности, рассматривается решение простейших уравнений и неравенств, содержащих модуль, изучаются свойства арифметического квадратного корня; в 11 – м классе понятие встречается в разделе «Корень n -ой степени».

Опыт преподавания показывает, что учащиеся часто сталкиваются с трудностями при решении заданий, требующих знания данного материала, а нередко пропускают, не приступая к выполнению. В текстах экзаменационных заданий за курс 9 – ого и 11 – ого классов также включены подобные задания. Кроме того, требования, которые предъявляют к выпускникам школ Вузы отличаются, а именно, более высокого уровня, чем требования школьной программы.

Для жизни в современном обществе очень важным является формирование математического стиля мышления, проявляющегося в определённых умственных навыках. В процессе решения задач с модулями требуется умение применять такие приёмы, как обобщение и конкретизация, анализ, классификация и систематизация, аналогия. Решение подобных заданий позволяет проверить знание основных разделов школьного курса, уровень логического мышления, первоначальные навыки исследовательской деятельности.

Данная работа посвящена одному из разделов – решению уравнений, содержащих модуль. Она состоит из трёх глав. В первой главе вводятся основные понятия и наиболее важные теоретические выкладки. Во второй главе предлагаются девять основных типов уравнений, содержащих модуль, рассматриваются методы их решения, разбираются примеры разного уровня сложности. В третьей главе предлагаются более сложные и нестандартные уравнения (тригонометрические, показательные, логарифмические и иррациональные). К каждому типу уравнений есть упражнения для самостоятельного решения (ответы и указания прилагаются).

Основное назначение данной работы – это оказание методической помощи преподавателям при подготовке к урокам и при организации факультативных курсов. Материал также может быть использован в качестве учебного пособия для старшеклассников. Задания, предлагаемые в работе, интересны и не всегда просты в решении, что позволяет сделать учебную мотивацию учащихся более осознанной, проверить свои способности, повысить уровень подготовки выпускников школ к поступлению в Вузы. Дифференцированный подбор предлагаемых упражнений предполагает переход от репродуктивного уровня усвоения материала к творческому, а также возможность научить применять свои знания при решении нестандартных задач.

Глава 1. Введение.

Раздел 1. Определение абсолютной величины .

Определение : Абсолютной величиной (модулем) действительного числа а называется

неотрицательное число: а или –а.

Обозначение: │ а │ Запись читается следующим образом: «модуль числа а» или

«абсолютная величина числа а»

│ а│ = │ 0, если а = 0 (1)

Примеры: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 — √2│ = √2 – 1

Раскрыть модуль выражения:

а) │х — 8│, если х > 12 б) │2х + 3│, если х ≤ -2

│х – 8│= х – 8 │ 2х + 3│= — 2х – 3

Раздел 2. Основные свойства.

Рассмотрим основные свойства абсолютной величины.

Свойство №1: Противоположные числа имеют равные модули, т.е. │а│=│- а│

Покажем верность равенства. Запишем определение числа – а :

│ — а│ = 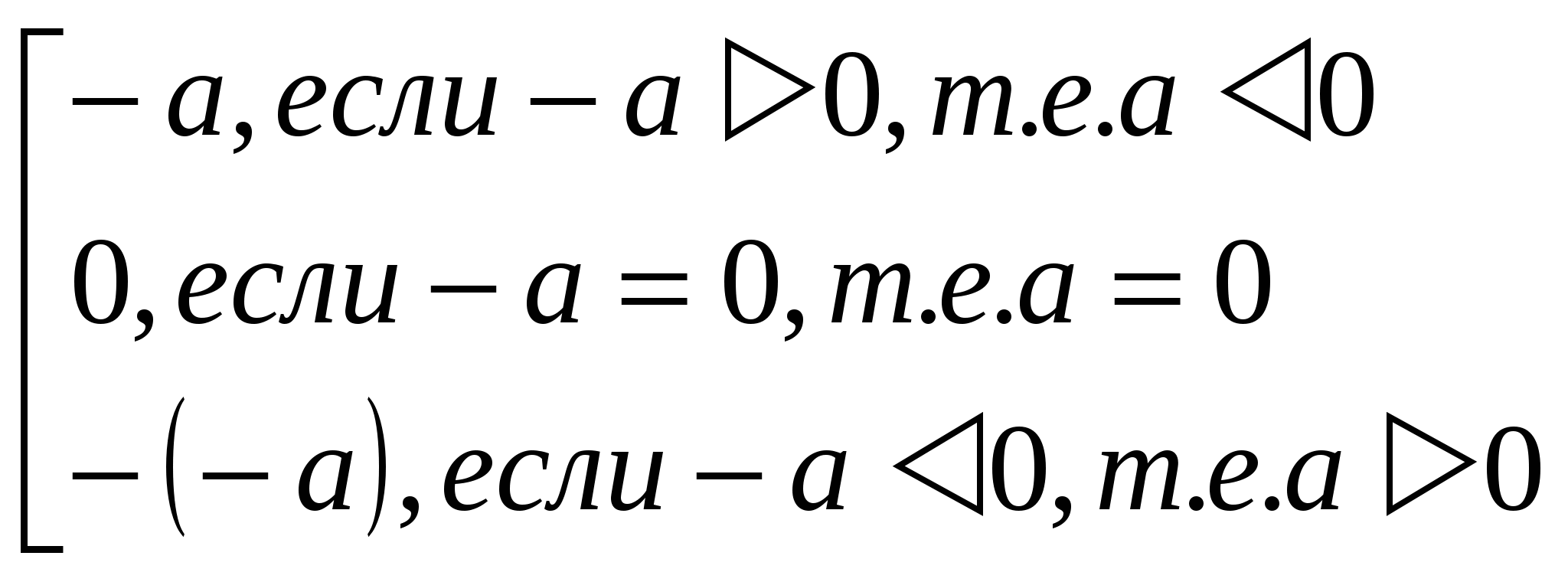(2)

Сравним совокупности (1) и (2). Очевидно, что определения абсолютных величин чисел а и – а совпадают. Следовательно, │а│=│- а│

При рассмотрении следующих свойств ограничимся их формулировкой, так как их доказательство приводится в

Свойство №2: Абсолютная величина суммы конечного числа действительных

чисел не превосходит суммы абсолютных величин слагаемых:

│а 1 + а 2 +…+ а n │ ≤│а 1 │+│а 2 │+ … + │а n │

Свойство №3: Абсолютная величина разности двух действительных чисел не

превосходит суммы их абсолютных величин: │а — в│ ≤│а│+│в│

Свойство №4: Абсолютная величина произведения конечного числа

действительных чисел равна произведению абсолютных величин

множителей: │а · в│=│а│·│в│

Свойство №5: Абсолютная величина частного действительных чисел равна

частному их абсолютных величин:

Раздел 3. Геометрическая интерпретация понятия модуля числа.

Каждому действительному числу можно поставить в соответствие точку на числовой прямой, которая будет геометрическим изображением данного действительного числа. Каждой точке на числовой прямой соответствует её расстояние от начала отсчёта, т.е. длина отрезка от начала отсчёта до данной точки. Это расстояние рассматривается всегда как величина неотрицательная. Поэтому длина соответствующего отрезка и будет геометрической интерпретацией абсолютной величины данного действительного числа

Представленная геометрическая иллюстрация наглядно подтверждает свойство №1, т.е. модули противоположных чисел равны. Отсюда легко понимается справедливость равенства: │х – а│= │а — х│. Также более очевидным становиться решение уравнения │х│= m , где m ≥ 0, а именно х 1,2 = ± m .

Примеры: 1) │х│= 4 х 1,2 = ± 4 2) │х — 3│= 1 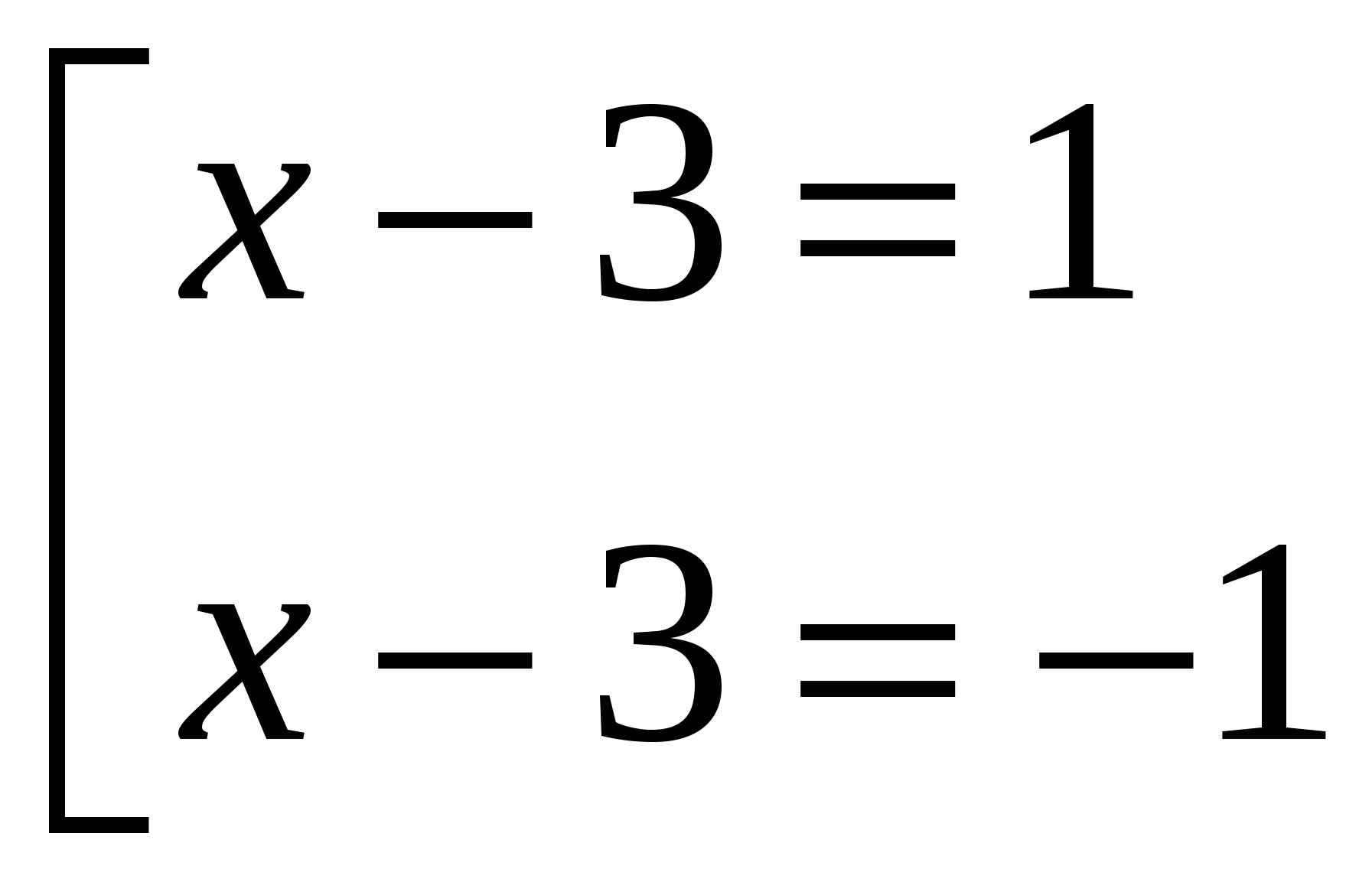х 1,2 = 2; 4

Раздел 4. График функции у = │х│

Область определения данной функции все действительные числа.

Раздел 5. Условные обозначения.

В дальнейшем при рассмотрении примеров решения уравнений будут использованы следующие условные обозначения:

При решение системы уравнений (неравенств) находится пересечение решений входящих в систему уравнений (неравенств). При решении совокупности уравнений (неравенств) находится объединение решений входящих в совокупность уравнений (неравенств).

Глава 2. Решение уравнений, содержащих модуль.

В этой главе мы рассмотрим алгебраические способы решения уравнений, содержащих один или более модуль.

Раздел 1. Уравнения вида │ F ( х )│= m

Уравнение данного вида называется простейшим. Оно имеет решение тогда и только тогда, когда m ≥ 0. По определению модуля, исходное уравнение равносильно совокупности двух уравнений:

│ F (х)│= m

№ 1. Решите уравнение:

│7х — 2│= 9

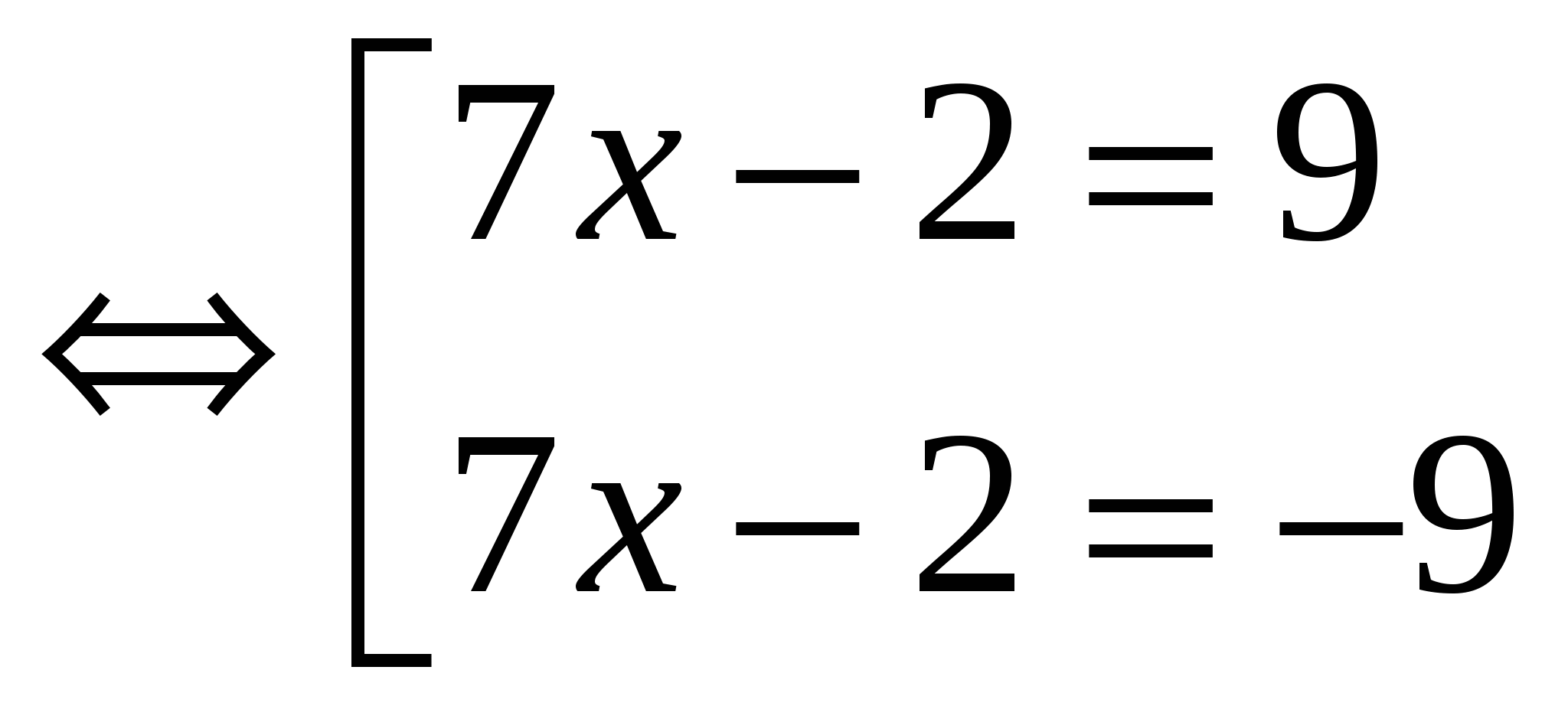
Ответ: х 1 = — 1; х 2 = 1 4 / 7

№ 2 . Решите уравнение, в ответе укажите сумму корней:

│х 2 + 3х + 1│= 1

х 2 + 3х + 2 = 0 х 2 +3х = 0

х 1 = -1; х 2 = -2 х · ( х + 3) = 0

Ответ: сумма корней равна — 2 .

№ 3 . Решите уравнение, в ответе укажите количество корней:

│х 4 -5х 2 + 2│= 2

х 4 – 5х 2 = 0 х 4 – 5х 2 + 4 = 0

х 2 · ( х 2 – 5) = 0 обозначим х 2 = m , m ≥ 0

х = 0; ±√5 m 2 – 5 m + 4 = 0

m = 1; 4 – оба значения удовлетворяют условию m ≥ 0

Ответ: количество корней уравнения 7.

№ 1. Решите уравнение и укажите сумму корней: │х — 5│= 3

№ 2 . Решите уравнение и укажите меньший корень: │х 2 + х│= 0

№ 3 . Решите уравнение и укажите больший корень: │х 2 – 5х + 4│= 4

№ 4 .Решите уравнение и укажите целый корень: │2х 2 – 7х + 6│= 1

№ 5 .Решите уравнение и укажите количество корней: │х 4 – 13х 2 + 50│= 14

Раздел 2. Уравнения вида F (│х│) = m

Аргумент функции в левой части находится под знаком модуля, а правая часть не зависит от переменной. Рассмотрим два способа решения уравнений данного вида.

1 способ: По определению абсолютной величины исходное уравнение равносильно совокупности двух систем. В каждой из которых накладывается условие на подмодульное выражение.

F (│х│) = m

Так как функция F (│х│) – чётная на всей области определения, то корни уравнений F (х) = m и F (- х) = m – это пары противоположных чисел. Поэтому достаточно решить одну из систем (при рассмотрении примеров указанным способом будет приводиться решение одной системы).

2 способ: Применение метода введения новой переменной. При этом вводиться обозначение │х│= а, где а ≥ 0. Данный способ менее объёмный по оформлению.

№ 1 . Решите уравнение:

3х 2 – 4│х│= — 1 Воспользуемся введением новой переменной. Обозначим │х│= а,

где а ≥ 0. Получим уравнение 3а 2 — 4а + 1 = 0

а 1 = 1 а 2 = 1 / 3

Возвращаемся к исходной переменной: │х│=1 и │х│= 1 / 3 . Каждое уравнение имеет

Ответ: х 1 = 1; х 2 = — 1; х 3 = 1 / 3 ; х 4 = — 1 / 3 .

№ 2. Решите уравнение:

5х 2 + 3│х│- 1 = 1 / 2 │х│ + 3х 2

Найдём решение первой системы совокупности: 4х 2 + 5х – 2 =0

Д = 57 х 1 = -5+√57 / 8 х 2 = -5-√57 / 8

Заметим, что х 2 не удовлетворяет условию х ≥ 0. Решением второй системы будет

число, противоположное значению х 1 .

Ответ: х 1 = -5+√57 / 8 ; х 2 = 5-√57 / 8 .

№ 3 . Решите уравнение:

Обозначим │х│= а, где а ≥ 0. Получим уравнение а 4 – а = 0

Возвращаемся к исходной переменной: │х│=0 и │х│= 1

Ответ: х 1 = 0; х 2 = 1; х 3 = — 1.

№ 6. Решите уравнение: 2│х│ — 4,5 = 5 – 3 / 8 │х│

№ 7 . Решите уравнение, в ответе укажите количество корней: 3х 2 — 7│х│ + 2 = 0

№ 8 . Решите уравнение, в ответе укажите целые решения: х 4 + │х│ — 2 = 0

Раздел 3. Уравнения вида │ F (х)│ = G (х)

Правая часть уравнения данного вида зависит от переменной и, следовательно, имеет решение тогда и только тогда, когда правая часть функция G (х) ≥ 0. Исходное уравнение можно решить двумя способами:

1 способ: Стандартный, основан на раскрытии модуля исходя из его определения и заключается в равносильном переходе к совокупности двух систем.

│ F (х)│ = G (х)

Данный способ рационально использовать в случае сложного выражения для функции G ( x ) и мене сложного – для функции F (х), так как предполагается решение неравенств с функцией F (х).

2 способ: Состоит в переходе к равносильной системе, в которой накладывается условие на правую часть.

│ F ( x )│= G ( x )

Данный способ удобнее применять, если выражение для функции G (х) мене сложное, чем для функции F (х), так как предполагается решение неравенства G (х) ≥ 0. Кроме того, в случае нескольких модулей этот способ рекомендуется применять второй вариант.

№ 1. Решите уравнение:

│х + 2│= 6 -2х 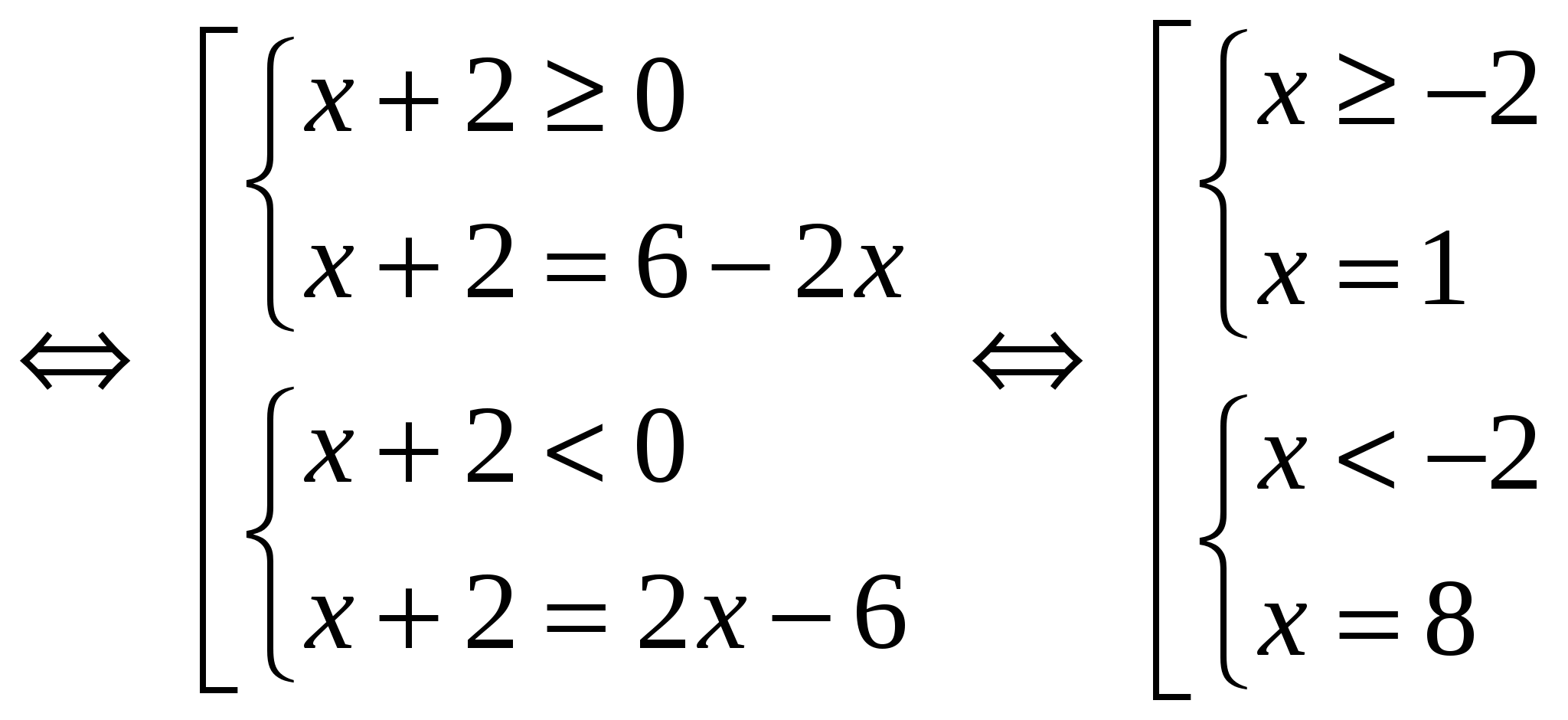(1 способ)

Ответ: х = 1 1 / 3

№ 2. Решите уравнение, в ответе укажите произведение корней:

│х 2 – 2х — 1│= 2·(х + 1)

(2 способ)

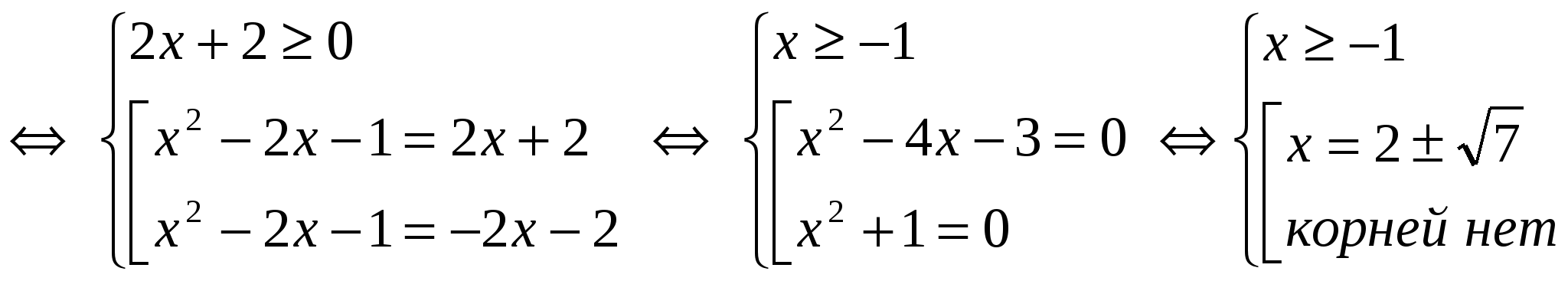
Ответ: Произведение корней – 3.

№ 3. Решите уравнение, в ответе укажите сумму корней:

│х — 6│= х 2 — 5х + 9

Ответ: сумма корней равна 4.

№ 9. Решите уравнение, в ответе укажите сумму корней:│х + 4│= — 3х

№ 10. Решите уравнение, в ответе укажите число решений:│х 2 + х — 1│= 2х – 1

№ 11 . Решите уравнение, в ответе укажите произведение корней:│х + 3│= х 2 + х – 6

Раздел 4. Уравнения вида │ F ( x )│= F ( x ) и │ F ( x )│= — F ( x )

Уравнения данного вида иногда называют «красивейшими». Так как правая часть уравнений зависит от переменной, решения существуют тогда и только тогда, когда правая часть неотрицательна. Поэтому исходные уравнения равносильны неравенствам:

│ F ( x )│= F ( x ) F ( x ) ≥ 0 и │ F ( x )│= — F ( x ) F ( x ) Примеры:

№ 1 . Решите уравнение, в ответе укажите меньший целый корень:

│5х — 3│= 5х – 3 5х – 3 ≥ 0

№ 2. Решите уравнение, в ответе укажите длину промежутка:

│х 2 — 9│= 9 – х 2 х 2 – 9 ≤ 0

Ответ: длина промежутка равна 6.

№ 3 . Решите уравнение, в ответе укажите число целых решений:

│2 + х – х 2 │= 2 + х – х 2 2 + х – х 2 ≥ 0

Ответ: 4 целых решения.

№ 4 . Решите уравнение, в ответе укажите наибольший корень:

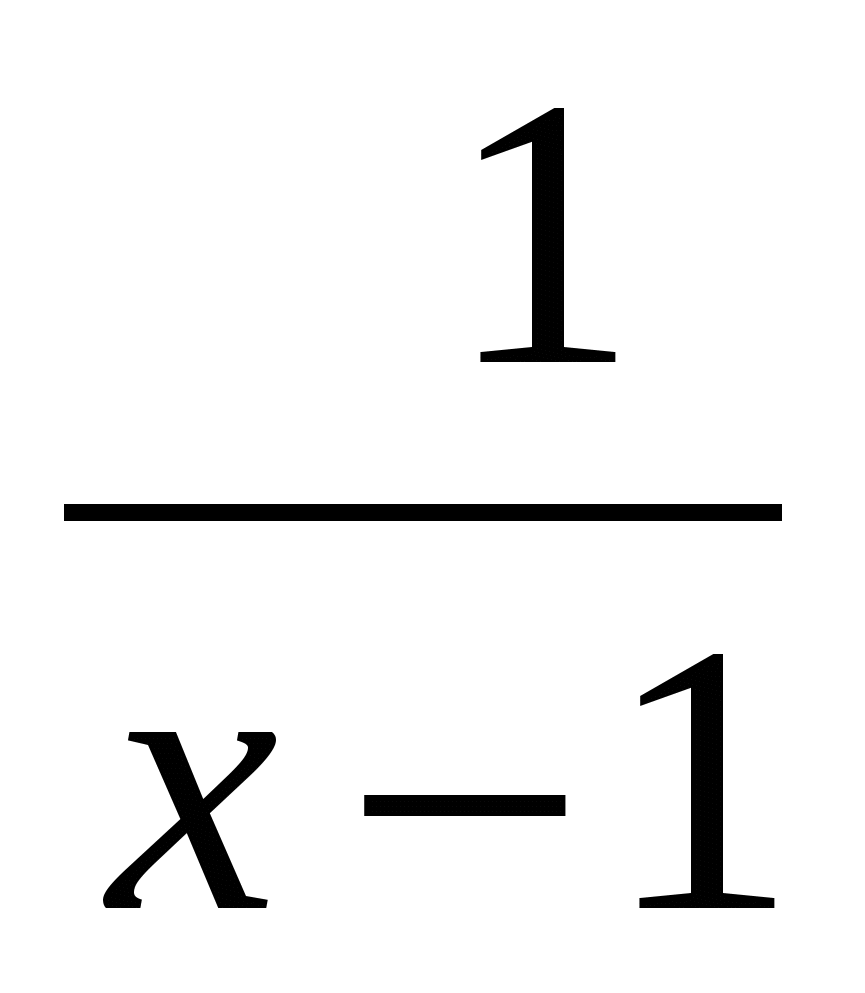
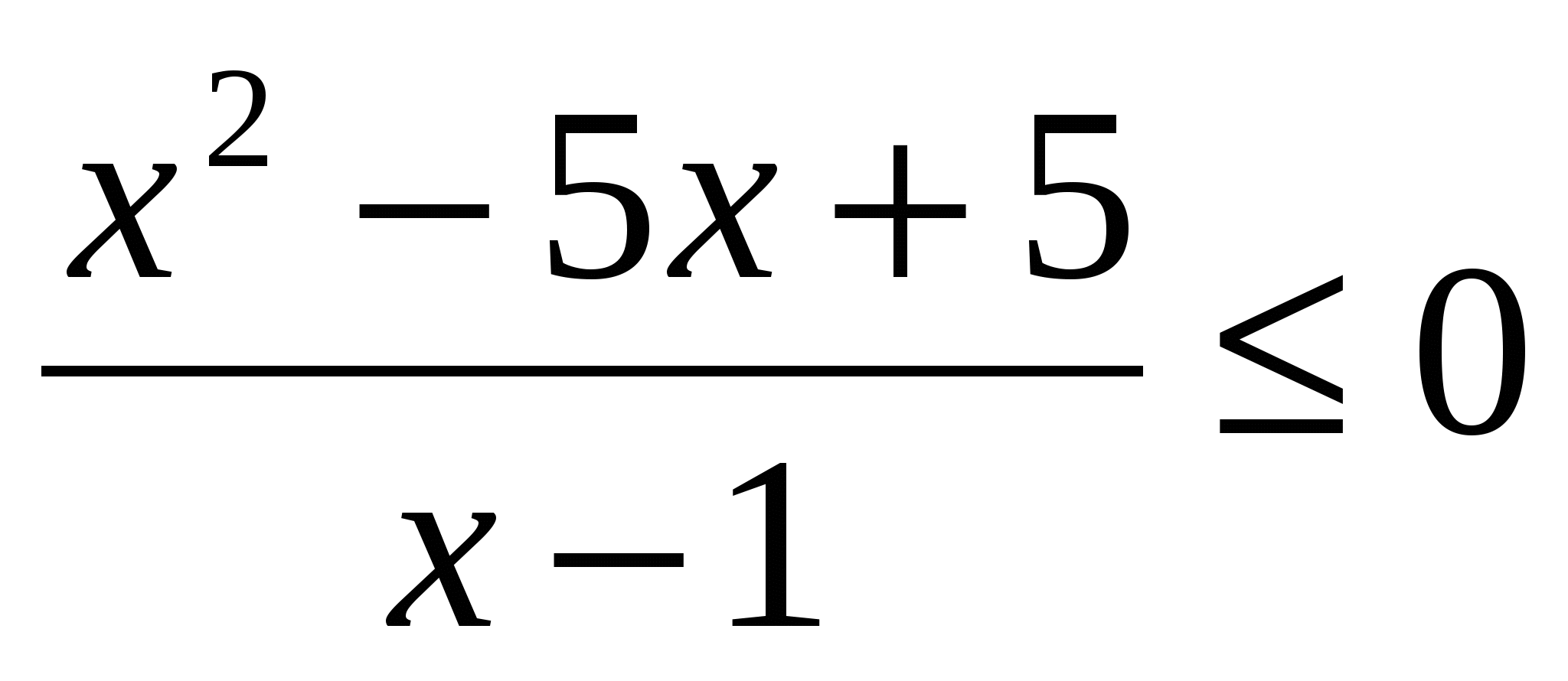
│4 – х — │= 4 – х –

х 2 – 5х + 5 = 0

Д = 5 х 1,2 = 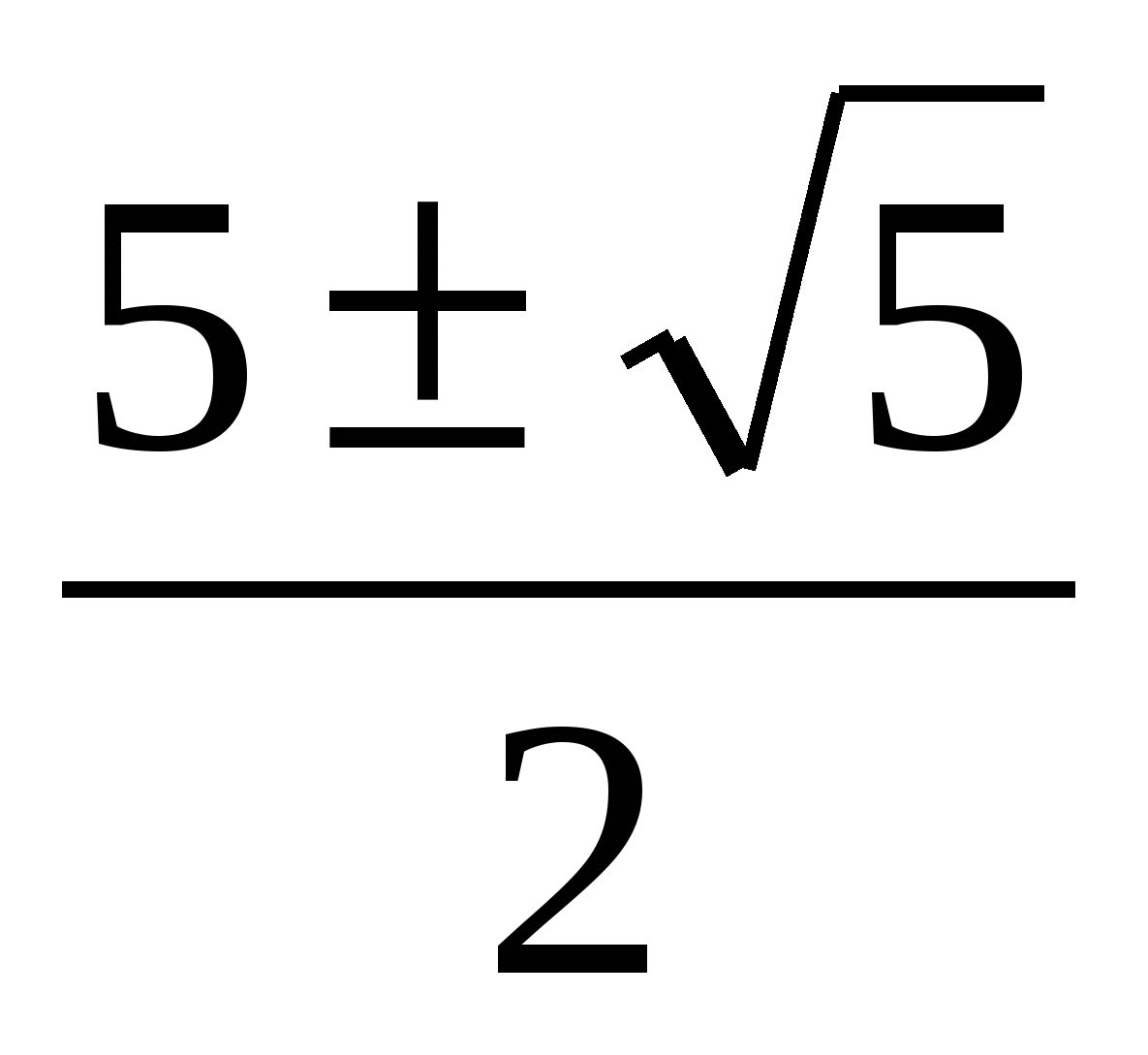≈ 1,4

№ 12. Решите уравнение, в ответе укажите целый корень: │х 2 + 6х + 8│= х 2 + 6х + 8

№ 13. Решите уравнение, в ответе укажите число целых решений:

│13х – х 2 — 36│+ х 2 – 13х + 36 = 0

№ 14. Решите уравнение, в ответе укажите целое число, не являющееся корнем уравнения:

Раздел 5. Уравнения вида │ F ( x )│= │ G ( x )│

Так как обе части уравнения неотрицательные, то решение предполагает рассмотрение двух случаев: подмодульные выражения равны или противоположны по знаку. Следовательно, исходное уравнение равносильно совокупности двух уравнений:

│ F ( x )│= │ G ( x )│

№ 1. Решите уравнение, в ответе укажите целый корень:

│х + 3│=│2х — 1│

Ответ: целый корень х = 4.

№ 2. Решите уравнение: │ х – х 2 — 1│=│2х – 3 – х 2 │

№ 3 . Решите уравнение, в ответе укажите произведение корней:

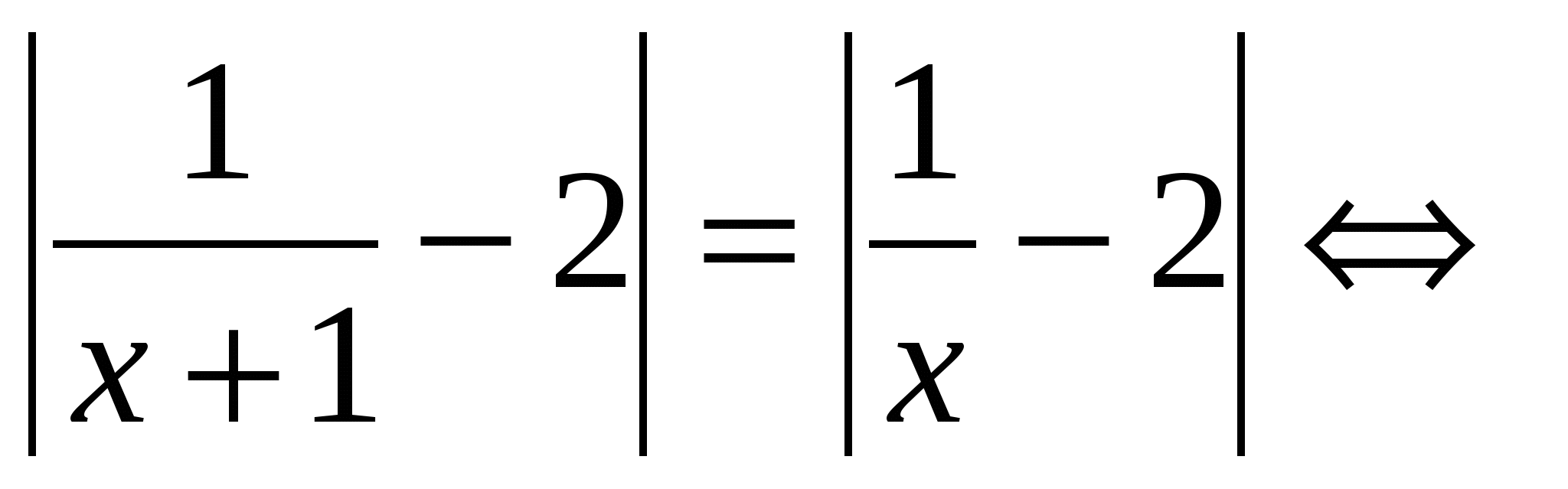
Корни уравнения 4х 2 + 2х – 1 = 0 х 1,2 = — 1±√5 / 4

Ответ: произведение корней равно – 0,25.

№ 15 . Решите уравнение, в ответе укажите целое решение:│х 2 – 3х + 2│= │х 2 + 6х — 1│

№ 16. Решите уравнение, в ответе укажите меньший корень:│5х — 3│=│7 — х│

№ 17 . Решите уравнение, в ответе укажите сумму корней:

Раздел 6. Примеры решения нестандартных уравнений

В данном разделе мы рассмотрим примеры нестандартных уравнений, при решении которых абсолютная величина выражения раскрывается по определению.

№ 1. Решите уравнение, в ответе укажите сумму корней:

х · │х│- 5х – 6 = 0

Ответ: сумма корней равна 1

№ 2. . Решите уравнение, в ответе укажите меньший корень:

х 2 — 4х · 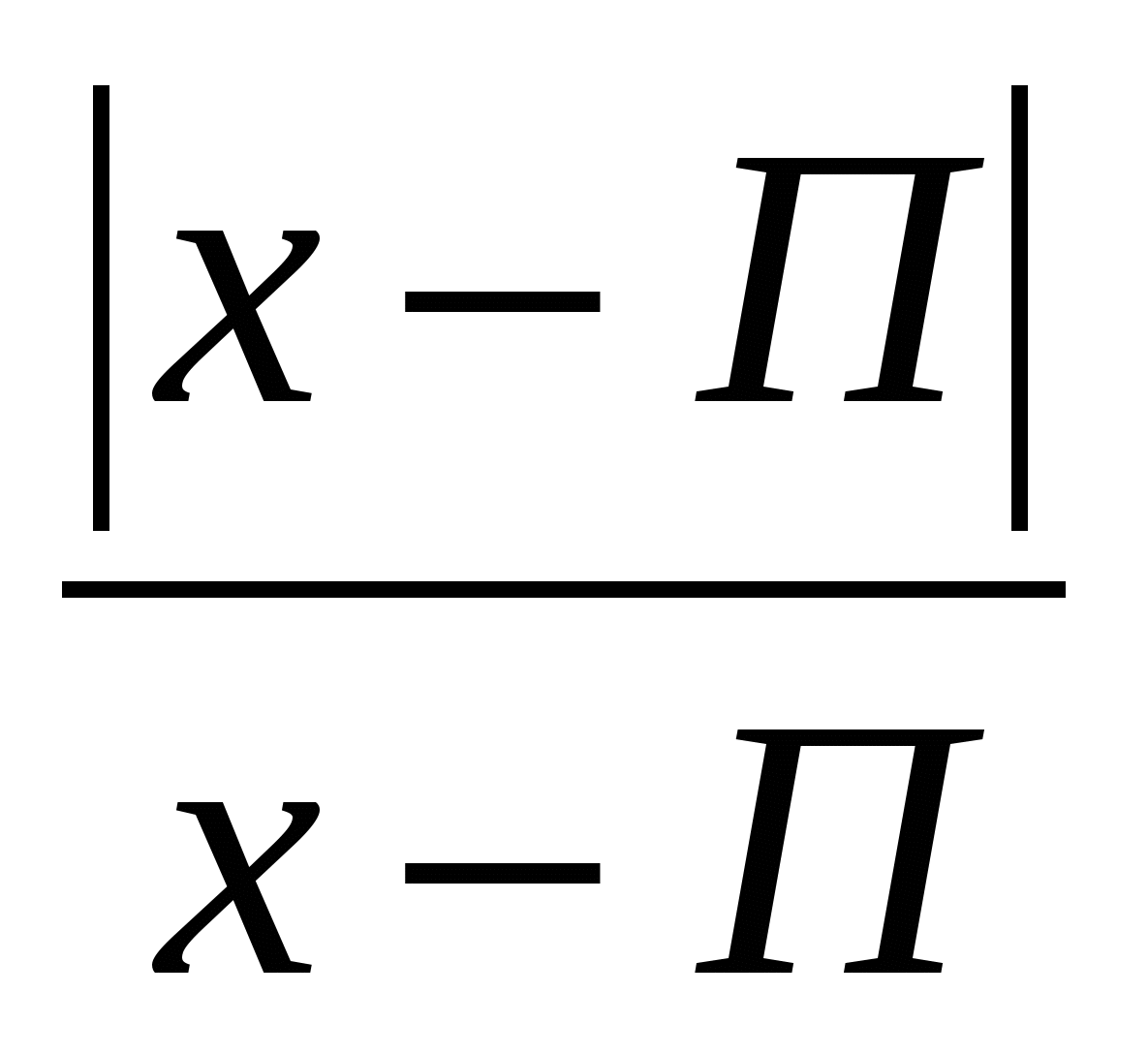— 5 = 0

Ответ: меньший корень х = — 5.

№ 3. Решите уравнение:

№ 18. Решите уравнение и укажите сумму корней: х · │3х + 5│= 3х 2 + 4х + 3

№ 19. Решите уравнение: х 2 – 3х =

№ 20. Решите уравнение:

Раздел 7. Уравнения вида │ F ( x )│+│ G ( x )│=0

Нетрудно заметить, что в левой части уравнения данного вида сумма

неотрицательных величин. Следовательно, исходное уравнение имеет решение тогда и

только тогда, когда оба слагаемых одновременно равны нулю. Уравнение равносильно

│ F ( x )│+│ G ( x )│=0

№ 1 . Решите уравнение:

№ 2. Решите уравнение:

№ 21. Решите уравнение:

№ 22 . Решите уравнение, в ответе укажите сумму корней:

№ 23 . Решите уравнение, в ответе укажите количество решений:

Раздел 8. Уравнения вида │а 1 х + в 1 │±│а 2 х + в 2 │± … │а n х +в n │= m

Для решения уравнений данного вида применяется метод интервалов. Если его решать последовательным раскрытием модулей, то получим n совокупностей систем, что очень громоздко и неудобно. Рассмотрим алгоритм метода интервалов:

1). Найти значения переменной х , при которых каждый модуль равен нулю (нули подмодульных выражений):

2). Найденные значения отметить на числовой прямой, которая разбивается на интервалы (количество интервалов соответственно равно n +1 )

3). Определить, с каким знаком раскрывается каждый модуль на каждом из полученных интервалов (при оформлении решения можно использовать числовую прямую, отметив на ней знаки)

4). Исходное уравнение равносильно совокупности n +1 систем, в каждой из которых указывается принадлежность переменной х одному из интервалов.

№ 1 . Решите уравнение, в ответе укажите наибольший корень:

1). Найдём нули подмодульных выражений: х = 2; х = -3

2). Отметим найденные значения на числовой прямой и определим, с каким знаком раскрывается каждый модуль на полученных интервалах:

2х + 6 2х + 6 2х + 6

3) — нет решений

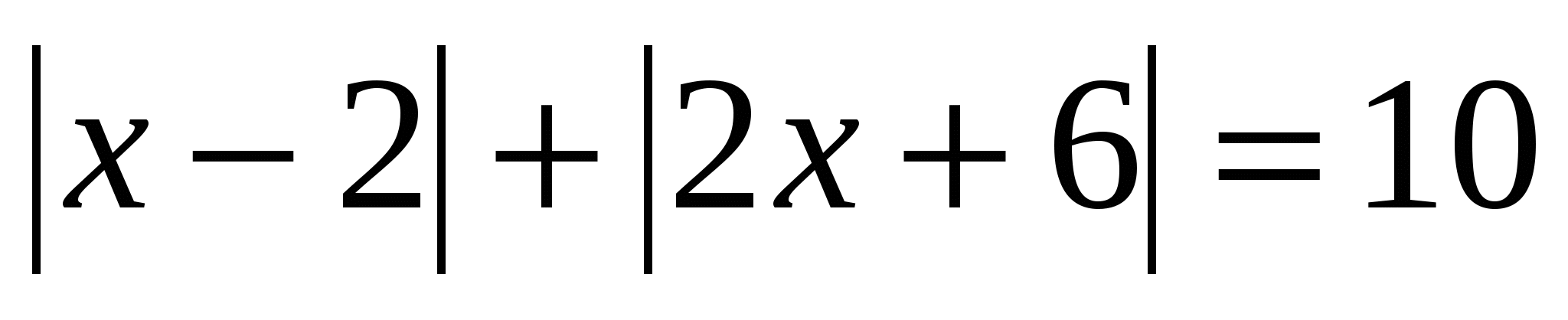
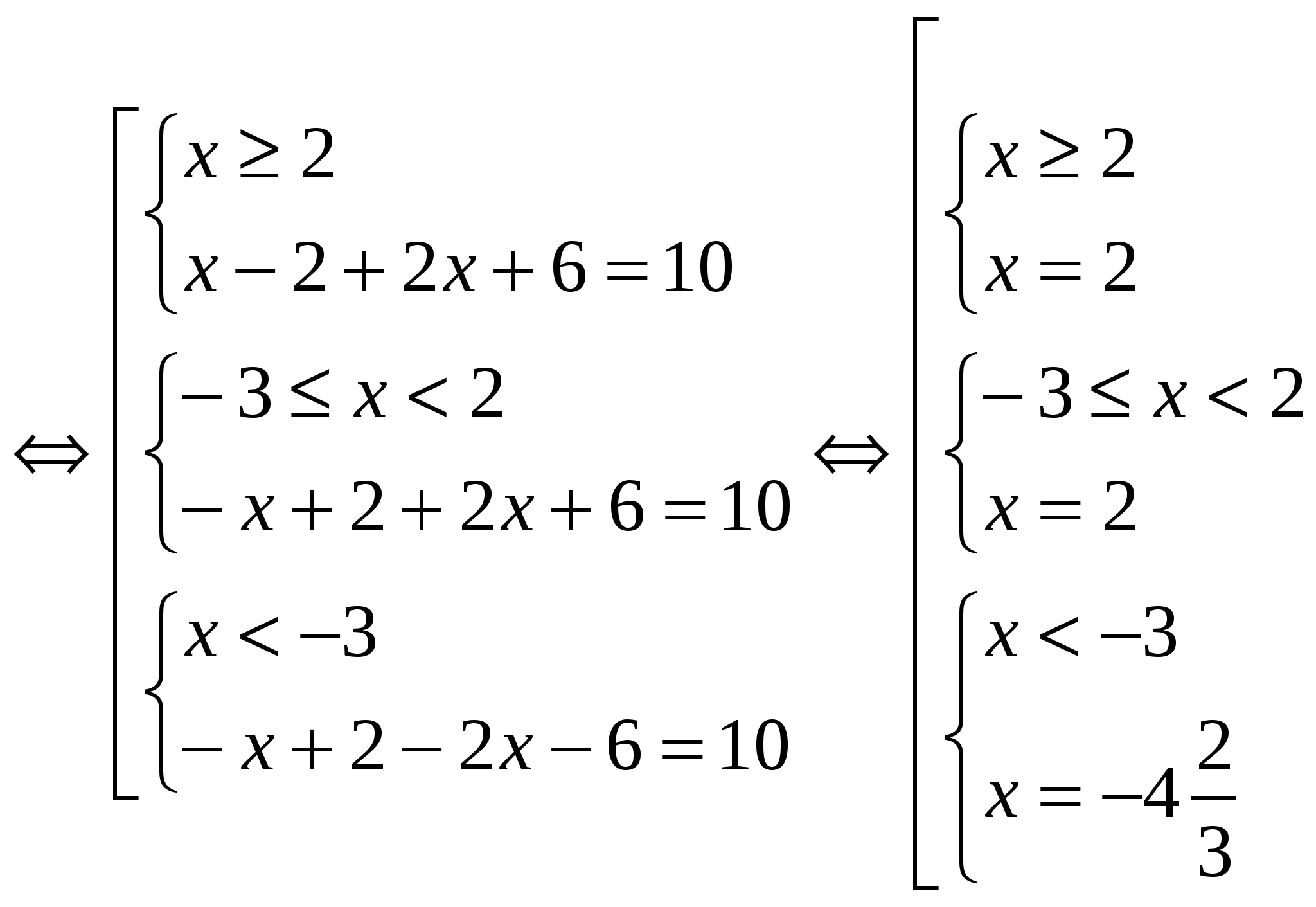
Уравнение имеет два корня.

Ответ: наибольший корень х = 2.

№ 2. Решите уравнение, в ответе укажите целый корень:

1). Найдём нули подмодульных выражений: х = 1,5; х = — 1

2). Отметим найденные значения на числовой прямой и определим, с каким знаком раскрывается каждый модуль на полученных интервалах:

2х – 3 2х – 3 2х – 3

3).

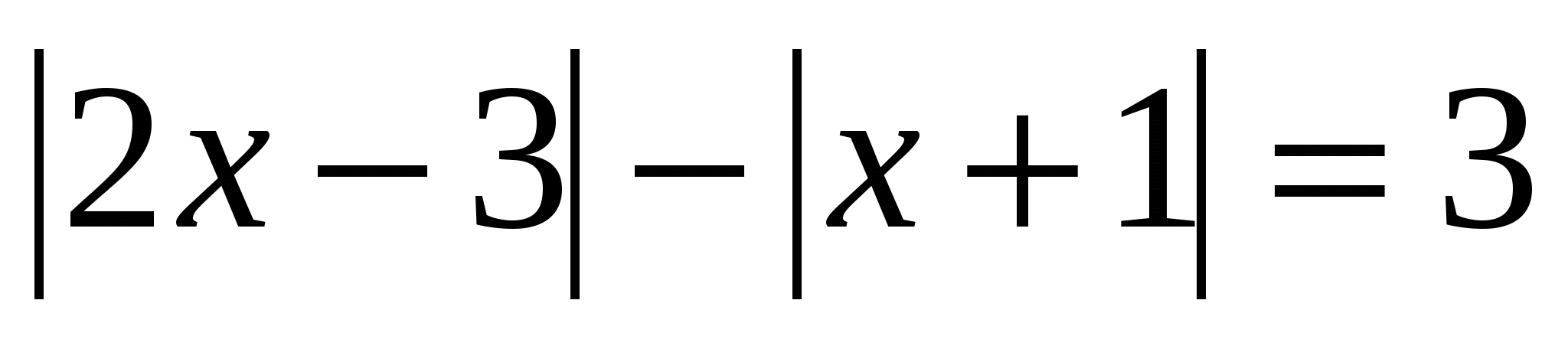
Последняя система не имеет решений, следовательно, уравнение имеет два корня. В ходе решения уравнения следует обратить внимание на знак « — » перед вторым модулем.

Ответ: целый корень х = 7.

№ 3. Решите уравнение, в ответе укажите сумму корней:

1). Найдём нули подмодульных выражений: х = 5; х = 1; х = — 2

2). Отметим найденные значения на числовой прямой и определим, с каким знаком раскрывается каждый модуль на полученных интервалах:

х – 5 х – 5 х – 5 х – 5

х – 1 х – 1 х – 1 х – 1

х + 2 х + 2 х + 2 х + 2

3).

Уравнение имеет два корня х = 0 и 2.

Ответ: сумма корней равна 2.

№ 4 . Решите уравнение:

1). Найдём нули подмодульных выражений: х = 1; х = 2; х = 3.

2). Определим, с каким знаком раскрывается каждый модуль на полученных интервалах.

3).

Объединим решения первых трёх систем.

№ 24. Решите уравнение:

№ 25. Решите уравнение, в ответе укажите сумму корней:

№ 26. Решите уравнение, в ответе укажите меньший корень:

№ 27. Решите уравнение, в ответе укажите больший корень:

Раздел 9. Уравнения, содержащие несколько модулей

Уравнения, содержащие несколько модулей, предполагают наличие абсолютных величин в подмодульных выражениях. Основной принцип решения уравнений данного вида – это последовательное раскрытие модулей, начиная с «внешнего». В ходе решения используются приёмы, рассмотренные в разделах №1, №3.

№ 1. Решите уравнение:

№ 2. Решите уравнение:

Ответ: х = 0; 4; — 4.

№ 3. Решите уравнение, в ответе укажите произведение корней:

Ответ: произведение корней равно – 8.

№ 4. Решите уравнение:

Обозначим уравнения совокупности (1) и (2) и рассмотрим решение каждого из них отдельно для удобства оформления. Так как оба уравнения содержат более одного модуля, то удобнее осуществить равносильный переход к совокупностям систем.

(1)

(2)

№ 5. Решите уравнение:

Каждое уравнение совокупности относится к виду F (│ x │) = m и равносильно совокупности двух систем:

В разделе 2 было замечено, что решением систем (1) и (2), (3) и (4) соответственно, являются пары противоположных чисел. Поэтому, достаточно решить системы (1) и (3).

Ответ: х = ± 1; ± (1+√2).

№ 28. Решите уравнение, в ответе укажите количество корней: │3 — │х — 2││=2

№ 29. Решите уравнение: ││х│+ х + 1│=1

№ 30 . Решите уравнение, в ответе укажите сумму корней: ││2х — 3│- 1│= х

№ 31 . Решите уравнение, в ответе укажите число решений: │х 2 -│х│- 1│= 1

Глава 3.

Примеры решения различных уравнений с модулем

Раздел 1. Тригонометрические уравнения

При рассмотрении следующих примеров используем определение модуля.

№ 1. Решите уравнение: sin 2 x = │ tg x │

О.Д.З. х R , х ≠ π/2 +π n , nZ

Данное уравнение равносильно совокупности двух систем, в каждой из которых

накладывается условие на подмодульное выражение. Для удобства рассмотрим

решение систем отдельно.

1) если tg х 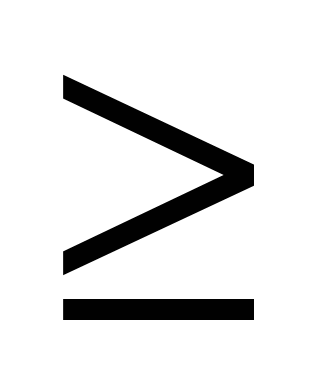0, то уравнение принимает вид sin 2 x = tg x

2 sin x · cos x =

Обе части уравнения умножим на cos х, получим

2sin x ·cos 2 x = sin x

sin x (2cos 2 x – 1) = 0

sin x = 0 или cos 2 x = 1 / 2

х 1 = π n, nZ cos x = √2 / 2 и cos x = — √2 / 2

х 2,3 = ± π / 4 +2πк, к Z х 4,5 = ± 3π / 4 +2π m , mZ

Проверим, удовлетворяют ли найденные решения условию tg x 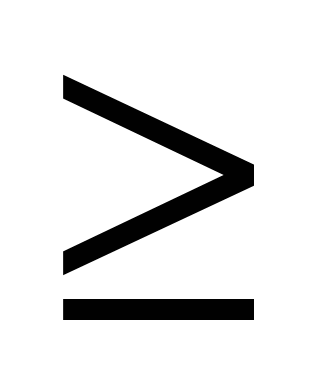0.

Этому условию удовлетворяют решения х 1 , х 2 , х 5 .

2) если tg x sin 2 x = — tg x

2sin x · cos x = —

Аналогично первому случаю, получаем

sin x = 0 или cos 2 x = — 1 / 2

х = π n , nZ нет корней

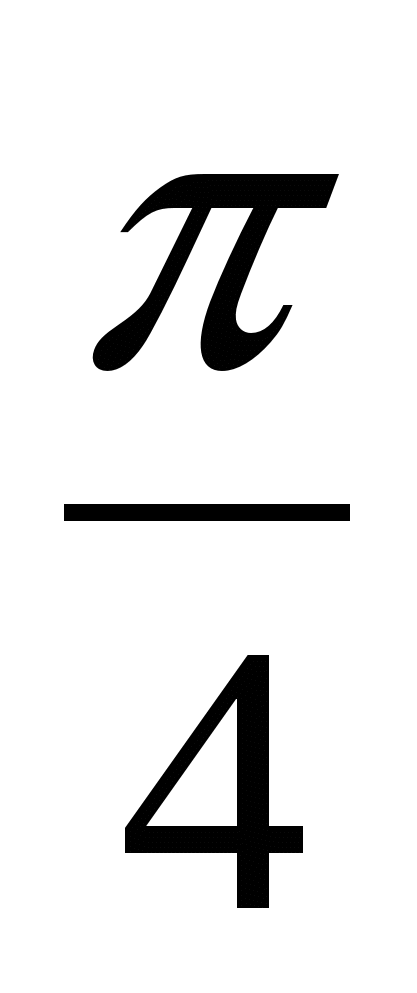
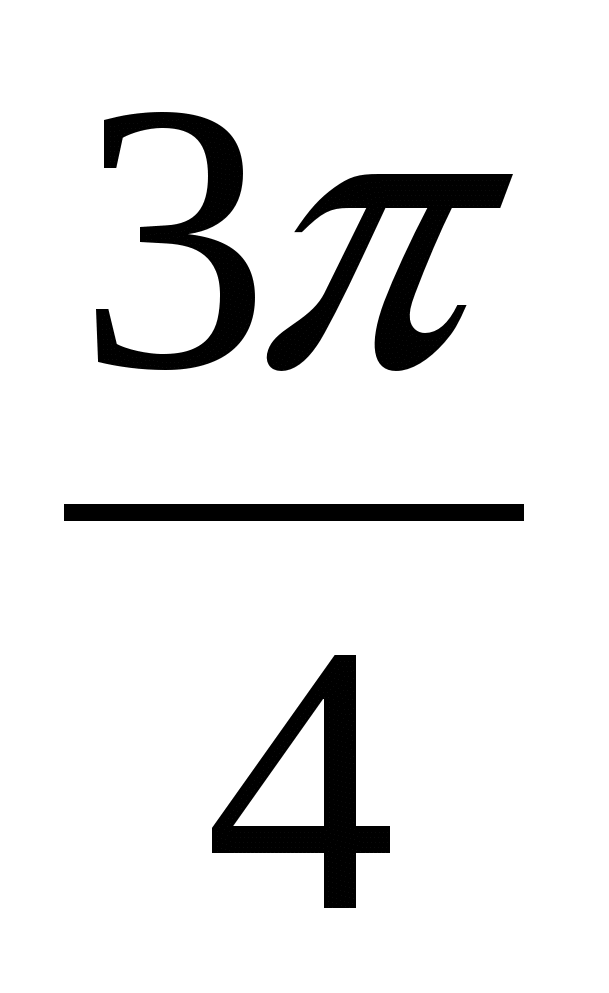
Решение х = π n не удовлетворяет условию tg х Ответ: х = π n , x = + 2πк, х = — + 2π m , где n , m , k Z

№ 2. Решите уравнение: │ sin x │= sin x + 2 cos x

О.Д.З. х R

Данное уравнение равносильно совокупности двух систем:

В уравнении (*) обе части разделим на sin x , т.к. sin x ≠ 0 и тогда ctg x = -1.

Проверим , удовлетворяют ли найденные решения условиям.

Решением системы (1) является значение х = 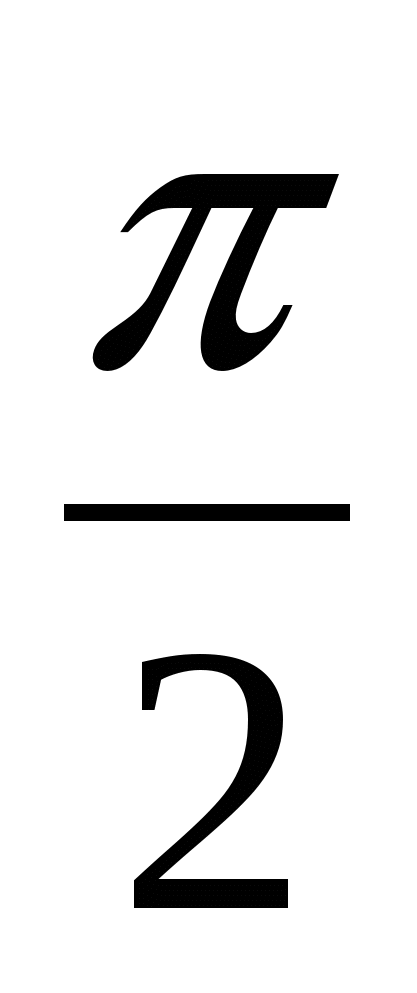+ 2π n , nZ , решением

системы (2) является значение х = 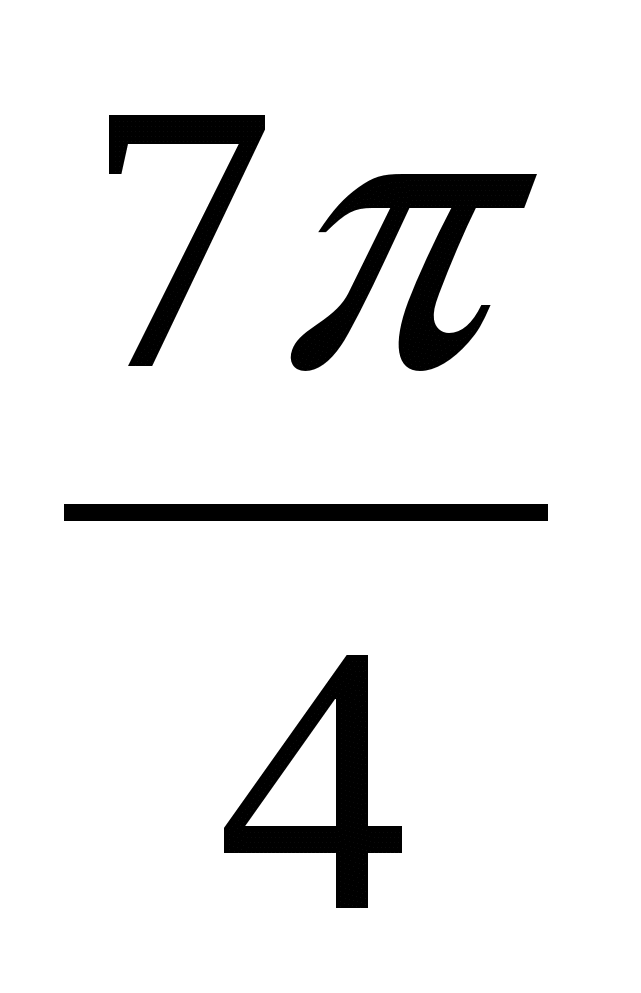+ 2πк, к Z .

Ответ: х =

№ 3. Решите уравнение: 2 cos x + │ cos x │= 2 sin 2 x · sin

О.Д.З. х R

Уравнение равносильно совокупности двух систем, решение которых

если cos 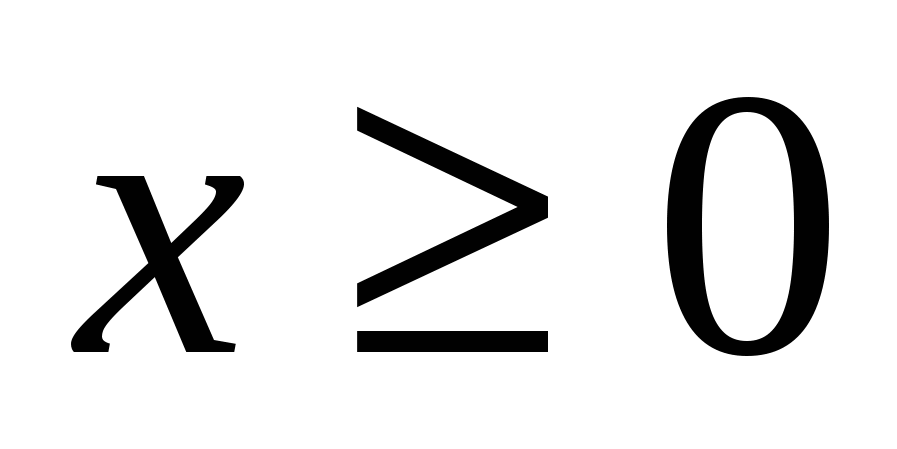, то получим следующее уравнение:

3 с os x – 2sin x · cos x = 0

cos x = 0 или sin x = 1,5

решений нет

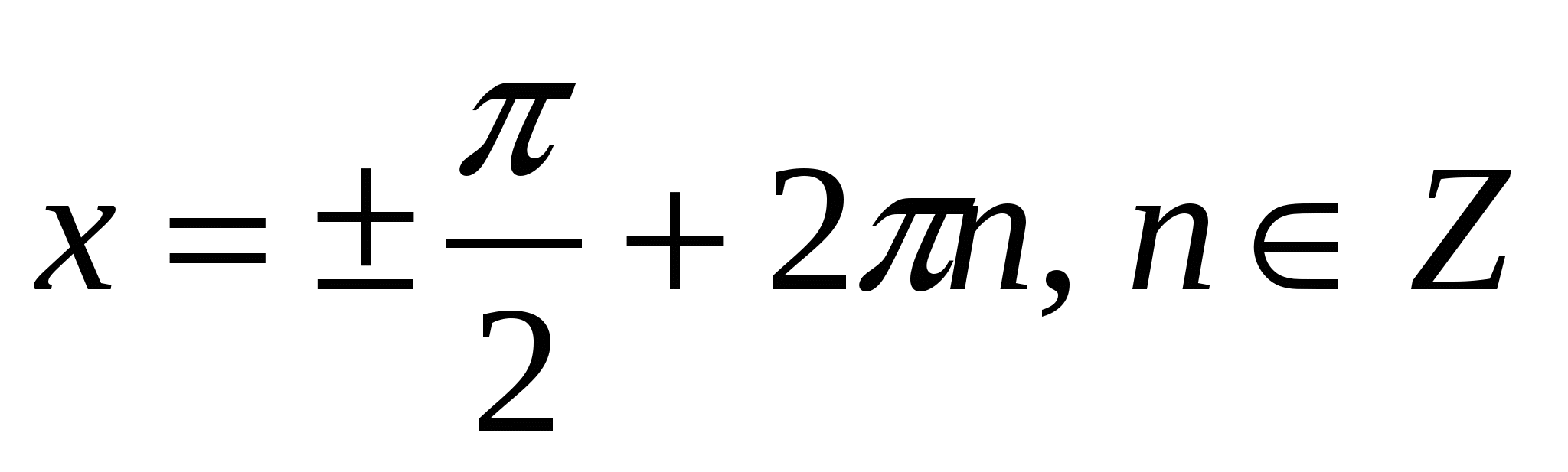
Найденное решение удовлетворяет условию cos x 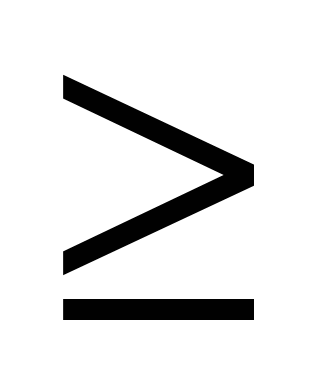0

если cos x cos x = 0 или sin x = 0,5

Условию cos x Ответ:

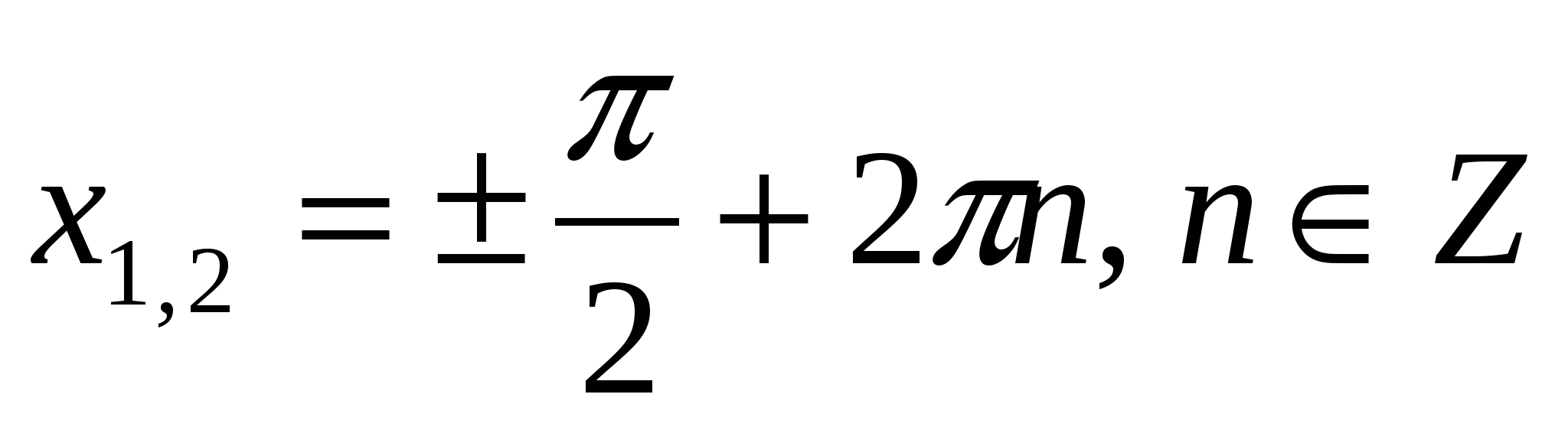
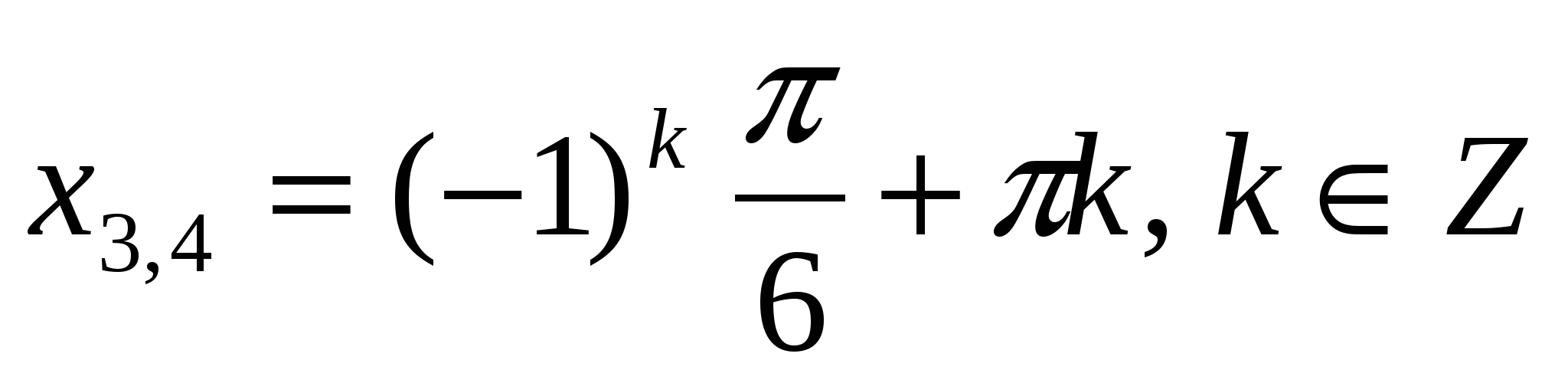
№ 4. Решите уравнение: 2 tg x + │ tg x │= sin 2 x

О.Д.З. cos x ≠ 0 , т.е.

Данное уравнение равносильно совокупности двух систем, решение

которых рассмотрим отдельно.

1) если tg x ≥ 0, то получим 2) если tg x sin x = 0 или с os 2 x = 1,5 sin x = 0 или cos 2 x = 0,5

x 1 = πn , nZ корней нет х 2 = πр, р Z cos x =

и

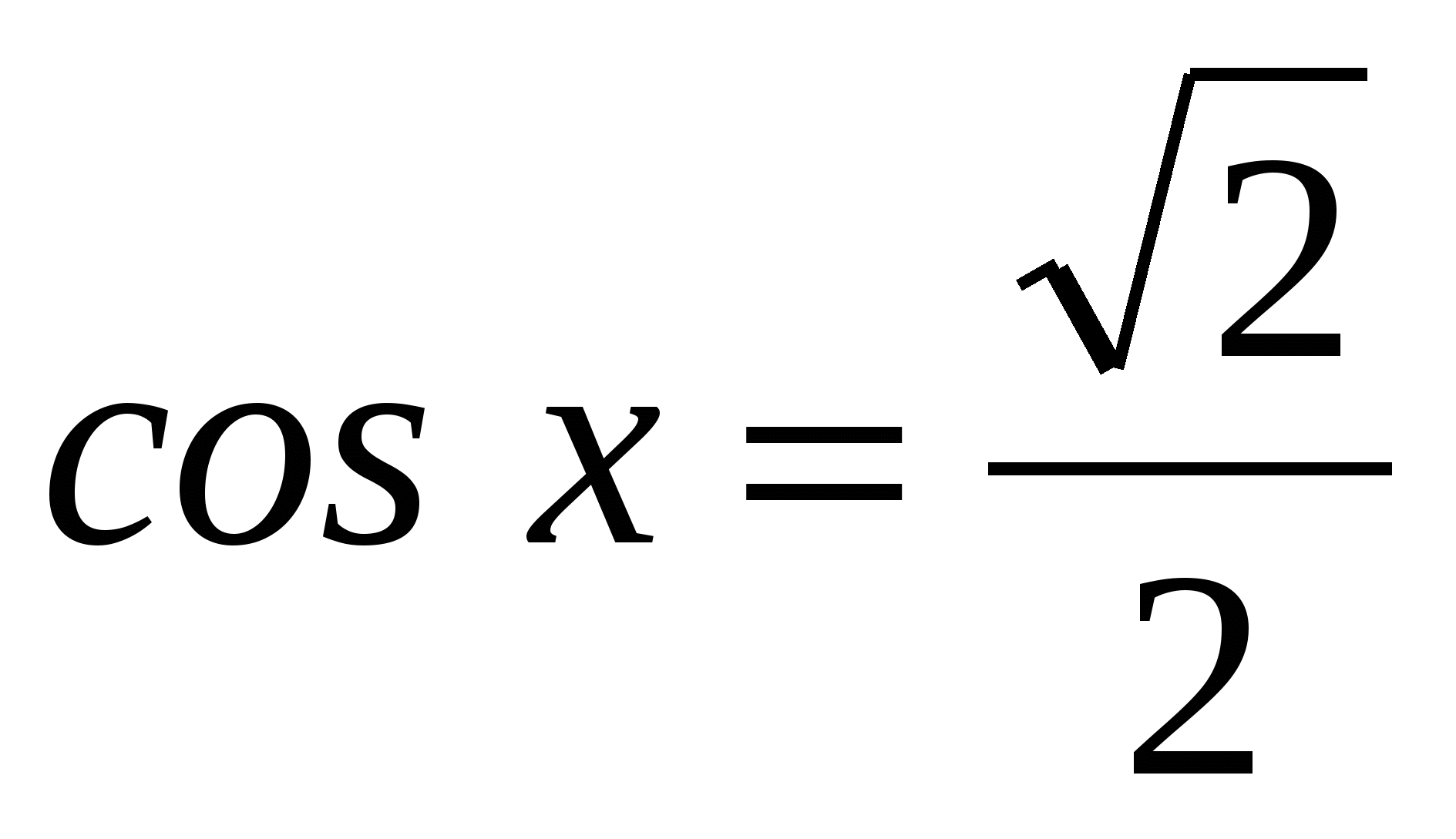
Условиям удовлетворяют решения х 1 , х 4 , х 5 .

Ответ:

№ 32. Решите уравнение: sin 2 x = │ sin x │

№ 33. Решите уравнение: 2│с os x │= ctg x

№ 34. Решите уравнение: 2 ctg x + │ ctg x │= sin 2 x

№ 35. Решите уравнение: 3 cos x — │ cos x │= 2 sin 2 x

Раздел 2. Показательные уравнения.

При рассмотрении следующих примеров используем определение модуля.

№ 1. Решите уравнение: 4 │х-2│ = 16 2х-1

О.Д.З. 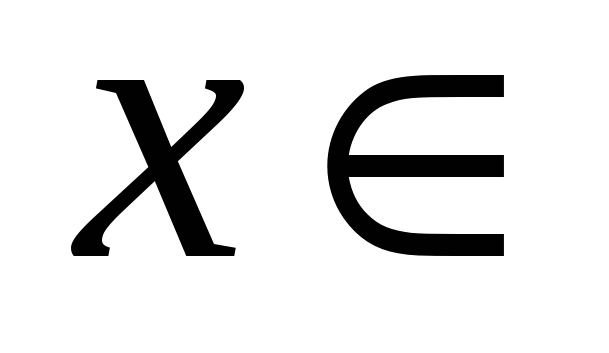R

Приведём обе части уравнения к степени с основанием 4.

4 │х-2│ = 4 4х-2

№ 2. Решите уравнение: │3 х — 6│+ 9 х – 6 = 0

О.Д.З. 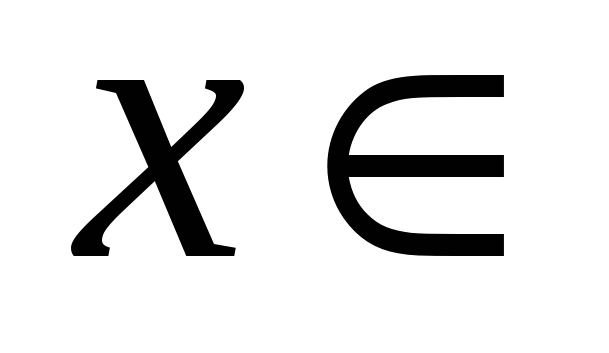R

Данное уравнение равносильно совокупности двух систем:

9 х + 3 х — 12 = 0 9 х – 3 х = 0

Обозначим 3 х = m , m > 0 Обозначим 3 х = m , m > 0

m 2 + m – 12 = 0 m 2 – m = 0

m 1 = 3; m 2 = — 4 m 1 = 1; m 2 = 0

№ 3. Решите уравнение, в ответе укажите произведение корней:

81 │х│ + 16 │х│ =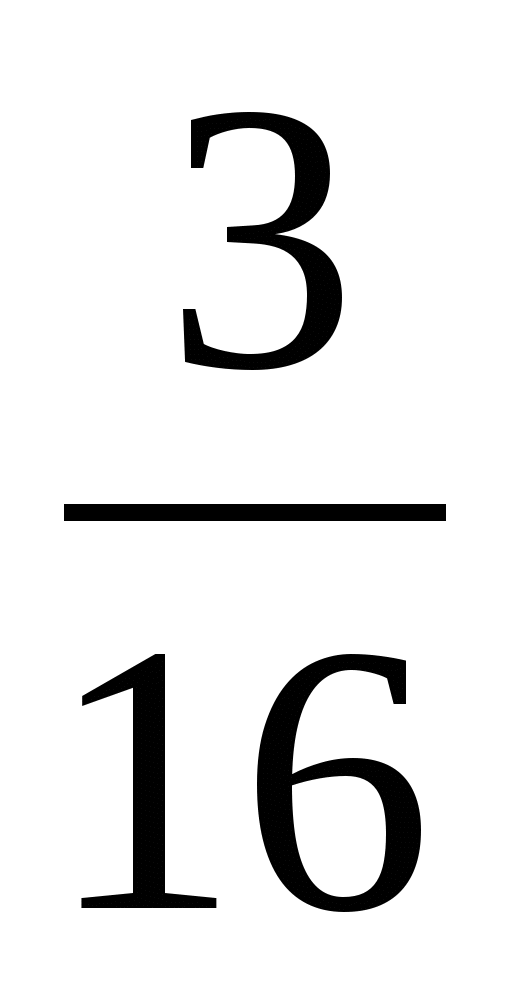· 36 │х│

Приведём показательную функцию к одному основанию, разделив обе части

уравнения на 16 │х│ .

m 2 — 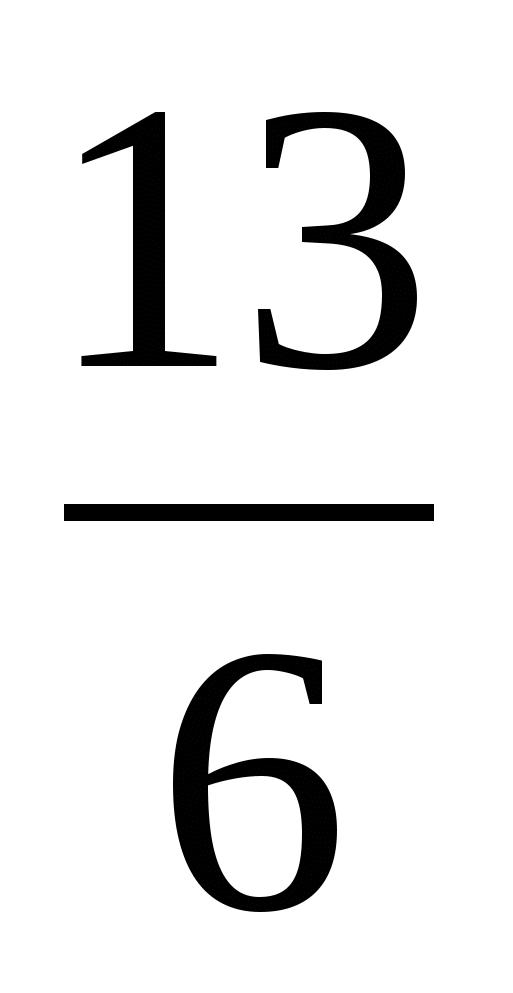m + 1 = 0

6 m 2 – 13 m + 6 = 0, Д=25, m 1 = 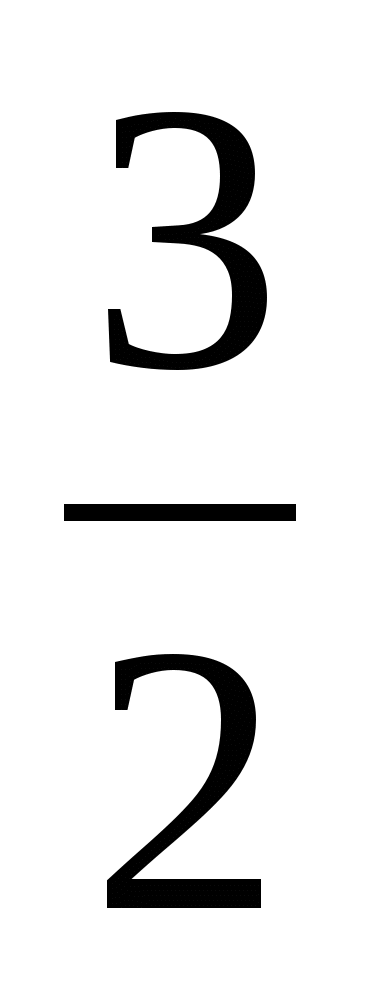, m 2 =

Ответ: произведение корней —

№ 4. Решите уравнение: 2 │3х — 5│ = 4 · 8 │х — 1│

2 │3х — 5│ = 2 2 · 2 3·│х — 1│

│3х — 5│ = 2 + 3 ·│х — 1│

│3х — 5│- 3 ·│х — 1│ = 2

Полученное уравнение решим методом интервалов.

Найдём нули подмодульных выражений: х = 1; 1.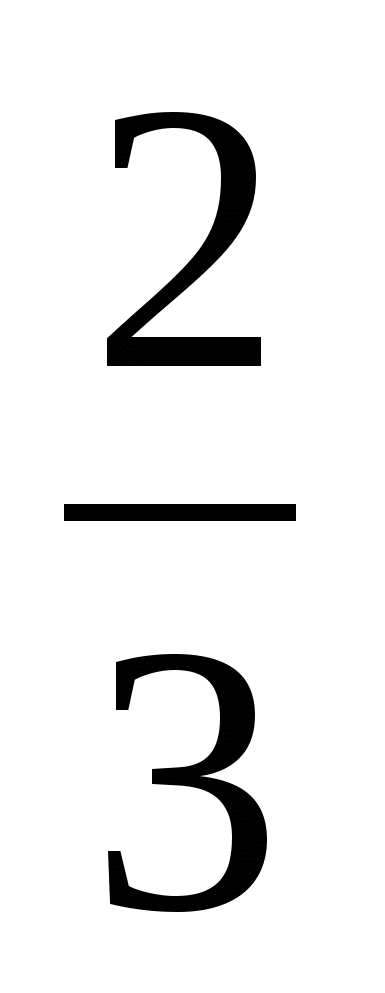

Эти числа разбивают числовую прямую на три интервала.

Уравнение равносильно совокупности трёх систем.

Ответ: (-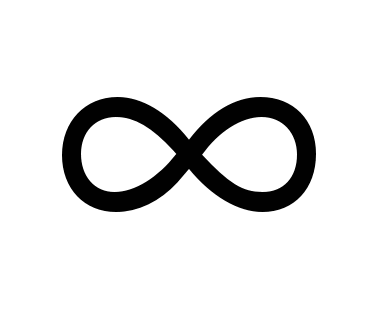; 1]

№ 36. Решите уравнение, в ответе укажите сумму корней: 5 │3х-5│ = 25 х

№ 37. Решите уравнение, если корней более одного, в ответе укажите сумму корней:

│х + 2│ х – 3х – 10 = 1

№ 38. Решите уравнение: 3 │2х -4│ = 9 │х│

№ 39. Решите уравнение, в ответе укажите количество корней на [0; 2π] : 2 │ sin х│ = √2

№ 40 . Решите уравнение, в ответе укажите количество корней:

Раздел 3. Логарифмические уравнения.

Перед решением следующих уравнений необходимо повторить свойства логарифмов

и логарифмической функции.

№ 1. Решите уравнение, в ответе укажите произведение корней:

log 2 (х+1) 2 + log 2 │ x +1│ = 6

1 случай: если х ≥ — 1, то log 2 ( x +1) 2 + log 2 ( x +1) = 6

log 2 (x+1) 3 = log 2 2 6

x = 3 – удовлетворяет условию х ≥ — 1

2 случай: если х log 2 ( x +1) 2 + log 2 (- x -1) = 6

log 2 (x+1) 2 + log 2 (-(x+1)) = 6

log 2 (-(x+1) 3 ) = log 2 2 6

x = — 5 – удовлетворяет условию х — 1

Ответ: произведение корней равно – 15.

№ 2. Решите уравнение, в ответе укажите сумму корней:

lg

О.Д.З.

Ответ: сумма корней равна 0,5.

№ 3. Решите уравнение: log 5

Исходное уравнение равносильно совокупности двух систем:

№ 4. Решите уравнение: │2 + log 0,2 x │+ 3 = │1 + log 5 x │

Воспользуемся формулой перехода к другому основанию.

│2 — log 5 x │+ 3 = │1 + log 5 x │

│2 — log 5 x │- │1 + log 5 x │= — 3

Найдём нули подмодульных выражений:

х = 25; х =

Эти числа делят область допустимых значений на три интервала, поэтому

уравнение равносильно совокупности трёх систем.

№ 41. Решите уравнение, в ответе кажите сумму корней: log 2 (│ x + 1│- 2) = — 2

№ 42. Решите уравнение, в ответе укажите сумму корней: log 2

№ 43. Решите уравнение: lg │2 x — 3│- lg │3 x — 2│= 1

№ 44. Решите уравнение, в ответе укажите наименьшее целое решение:

│1 + log 6 x │ + 2 = │3 + log 6 x │

№ 45. Решите уравнение: log

Список литературы:

1.Гайдуков И.И. «Абсолютная величина»

2.Литвиненко В.Н., Мордкович А.Г. «Практикум по решению математических задач»

3.Вавилов В.В. и другие «Задачи по математике. Уравнения и неравенства»

4. Черкасов О.Ю., Якушев А.Г. «Математика. Интенсивный курс подготовки к экзамену»

5.Дорофеев Г.В., Затахавай В.В. «Решение задач, содержащих модули и параметры»

6.Шарыгин И.Ф. «Факультативный курс по математике. Решение задач»

7.Виленкин Н.Я. и другие «Алгебра и математический анализ – 10 класс»

8.Ковалёва Г.И. и другие «Математика. Тренировочные тематические задания»

9.Куланин Е.Д. и другие «300 конкурсных задач по математике»

10.Ивлев Б.М. и другие « Задачи повышенной сложности по алгебре и началам анализа» 11.Гусев В.А. и другие « 1900 экзаменационных задач по математике»