Изучение логарифмов в старшей школе
Понятие логарифма
При решении показательных уравнений удается представить обе части уравнения в виде степеней с одинаковыми основаниями и рациональными показателями. Так, например, при решении уравнения 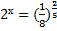
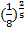
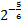
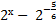
Действительно, если бы равенство 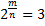
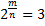
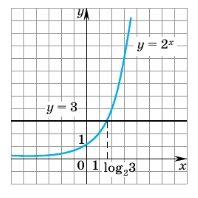
С другой стороны, график непрерывной функции y = 2 x пересекается с прямой y = 3, и, значит, уравнение 2 x = 3 имеет корень. Таким образом, перед нами стоят два вопроса: «Как записать этот корень?» и «Как его вычислить?».
Показатель степени, в которую нужно возвести число a (a > 0, a ≠ 1), чтобы получить число b, называется логарифмом b по основанию a и обозначается logab.
Теперь мы можем записать корень уравнения 2 х = 3:
Равенства a x = b и x = logab, в которых число a положительно и не равно единице, число b положительно, а число x может быть любым, выражают одно и то же соотношение между числами a, b и x. Подставив в первое равенство выражение x из второго, получим основное логарифмическое тождество.
Понятие логарифма в методическом пособии
Задание
Решите уравнение: а) 2 x = 64; б) 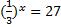
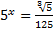
После проверки ученикам предлагается ответить на вопрос, какое из заданий показалось им наиболее трудным. Вероятный ответ: 2 (в), так как в нем нужно было приводить дробь к степени числа 5. Затем школьникам предлагается высказать мнение о сравнительной с заданием 2 (в) трудности уравнения 2 x = 3. На первый взгляд кажется, что это уравнение проще, однако представить 3 в виде степени числа 2 школьникам не удается.
Дальше изучение нового материала проводится в соответствии с учебником. При этом в зависимости от уровня класса рассматривается или не рассматривается дополнительный материал о невозможности представления 3 в виде 2 r , где r = m/n.
После этого диалог с классом можно строить примерно так:
— Как вы думаете, имеет ли уравнение 2 x = 3 корень? Ответ обоснуйте. [Если построить график функции у = 2 x и провести прямую у = 3, то они пересекутся в одной точке, значит, уравнение имеет один корень.]
— Что можно сказать о корне уравнения a x = b, где а > 0 и а ≠ 1? При всех ли значениях b оно имеет корни?
Затем вводится определение логарифма числа b по основанию а и записывается основное логарифмическое тождество 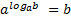
Логарифмическая функция
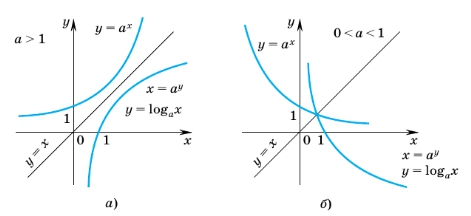
Выразим x из равенства y = logax, получим x = a y . Последнее равенство задает функцию x = a y , график которой симметричен графику показательной функции y = a x относительно прямой y = x.
Показательная функция x = a y является монотонной, и, значит, разные значения y соответствуют разным значениям x, но это говорит о том, что y = logax, в свою очередь, является функцией x.
Показательная функция y = a x и логарифмическая функция y = logax являются взаимно обратными. Сравнивая их графики, можно отметить некоторые основные свойства логарифмической функции.
Свойства функции y = logax, a > 0, a ≠ 11:
- Функция y = logax определена и непрерывна на множестве положительных чисел.
- Область значений функции y = logax — множество действительных чисел.
- При 0 1 функция y = logax является возрастающей.
- График функции y = logax проходит через точку (1; 0).
- Ось ординат — вертикальная асимптота графика функции y = loga.
Решение логарифмических уравнений и неравенств на основе свойств логарифмической функции
Освобождаясь от внешнего логарифма, имеющего основание 3, мы ссылаемся на возрастание соответствующей логарифмической функции, то есть на то, что большему значению логарифма соответствует большее значение выражения, стоящего под его знаком. Однако следует иметь в виду, что если функцию y = log3 log0,5(2x + 1) считать логарифмической, то ее аргумент не переменная x, а все выражение log0,5(2x + 1). Если же все-таки рассматривать x как аргумент функции y = log3 log0,5(2x + 1), то эта функция окажется убывающей, так как при увеличении значения x увеличивается значение выражения 2x + 1, уменьшается значение выражения log0,5(2x + 1) и, соответственно, уменьшается значение самой функции.
Свойства логарифмов
Связь двух форм записи соотношения между числами a, b и x (речь о a x = b и x = logab) позволяет получить свойства логарифмов, основываясь на известных свойствах степеней.
Рассмотрим, например, произведение степеней с одинаковым основанием: a x a y . Пусть a x = b и a y = c. Перейдем к логарифмической форме: x = logab и y = logac, тогда bc = a log a b × a log a c = a log a b + log a c . От показательной формы равенства bc = a log a b + log a c перейдем к логарифмической форме:
Заметим, что в левой части формулы числа a и b могут быть отрицательными. Тогда формула будет выглядеть так:
Аналогично можно получить еще два свойства для логарифмов частного и степени.
- логарифм произведения loga(bc) = loga|b| + loga|c|
- логарифм частного
- логарифм степени logabp= p loga|b|
Последнее свойство дает возможность вывести важную формулу, с помощью которой можно выразить логарифм с одним основанием через логарифм с другим основанием.
Пусть logab = x. Перейдем к показательной форме a x = b. Прологарифмируем это равенство по основанию c, т.е. найдем логарифмы с основанием c обеих частей этого равенства: logca x = logcb. Применяя к левой части свойство логарифма степени, получим x logca = logcb или 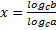
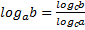
Формула перехода от одного основания логарифма к другому
Полезно запомнить частный случай формулы перехода, когда одно из оснований является степенью другого:
Рассмотренные свойства и формула перехода «работают», конечно, только когда все входящие в них выражения имеют смысл.
Логарифмы. Логарифмические уравнения. 11-й класс
Разделы: Математика
Класс: 11
Цели урока:
- Образовательные: отработка умений систематизировать, обобщать свойства логарифмов, логарифмической функции; применять их при решении логарифмических уравнений; уметь применять различные методы решения логарифмических уравнений.
- Развивающие: развитие сознательного восприятия учебного материала, развитие зрительной памяти, развитие математической речи учащихся. Формировать навыки самообучения, самоорганизации и самооценки, способствовать развитию исследовательской и творческой деятельности учащихся.
- Воспитательные: формирование познавательной активности; воспитать у учащихся любовь и уважение к предмету, научить видеть в математике не только строгость, сложность, но и логичность, простоту и красоту. (Слайд 2).
1. Организационный момент
а) Дорогие ребята! Я надеюсь, что этот урок пройдет интересно, с большой пользой для всех. Очень хочу, чтобы те, кто еще равнодушен к царице всех наук, с нашего урока ушел с глубоким убеждением: Математика – интересный и очень нужный предмет. Для того, чтобы выполнить все задания, вы должны уметь применять все приобретенные знания по логарифму, поэтому эпиграфом нашего урока будут слова:«Усердие все превозмогает».
б) Объявление темы урока, его цели:
Сегодня на уроке мы будем повторять.
Все свойства логарифмов подробно вспоминать.
Логарифмические уравнения с О.Д.З. решать.
Задания ЕГЭ С части разбирать.
На столе у каждого ученика лежит лист самооценки. После каждого этапа урока я рекомендую вам его заполнять.
Лист самооценки
Фамилия, имя ____________________________________________________
Этапы работы
Достижения
Количество баллов
Итоговое колличество баллов ____ Оценка ____
Критерии оценивания:
- «3» 10-15 баллов,
- «4» 16-30 баллов,
- «5» более 30 баллов. (Слайд 4).
2. Актуализация знаний
Логарифмом b по основанию a называется показатель степени, в которую надо возвести основание a, чтобы получить число b.
Значение основания a должно быть a > 0 и a =/= 1.
Число b принимает положительные значения.
Логарифм по основанию 10 называется десятичным.
Логарифм по основанию e называется натуральным. (Слайды5, 6).
Своиства логарифмов
График логарифмической функции
3. Устная работа
Ребята, вам даются задания, которые вы должны выполнить. Получив ответы к каждому заданию, внизу таблицы выберите свои ответы и рядом с заданием, в пустые клеточки впишите соответствующие значения букв.
| Н | Ю | Б | Е | П | Г | Т | И | В | Р |
| 3 | 0 | 1 | 4 | 0,6 | 0,5 | 5 | 49 | -3 | 2 |
4. Историческая справка
Джону Неперу принадлежит сам термин «логарифм», который он перевел как «искусственное число». Джон Непер – шотландец. В 16 лет отправился на континент, где в течение пяти лет в различных университетах Европы изучал математику и другие науки. Затем он серьезно занимался астрономией и математикой. К идее логарифмических вычислений Непер пришел еще в 80-х годах XVI века, однако опубликовал свои таблицы только в 1614 году, после 25-летних вычислений. Они вышли под названием «Описание чудесных логарифмических таблиц». (Слайд 10)
5. Исследовательская работа
«Исследование влияния преобразований логарифмических выражений на их область допустимых значений»
- Найдите ОДЗ уравнения log5(3x – 2) + log5(x – 7) = 2 + log52.
- Преобразуйте уравнение, используя свойства логарифмов.
- Найдите ОДЗ полученного уравнения и сравните её с исходной. Как изменилась ОДЗ (расширилась или сузилась)?
- Решите уравнение.
- Выполните проверку. Дайте ответ.
- Появились ли в ходе решения посторонние корни? Объясните причину их появления. (Слайды11, 12).
Вопросы:
1) Что происходит с ОДЗ при замене log2(x(x + 3))наlog2x + log2(x + 3 )?
2) Что происходит с ОДЗ при обратной замене?
3) В каком случае могут потеряться корни?
4) В каком случае могут образоваться посторонние корни?
Учащиеся высказывают свою гипотезу.
1) ОДЗ сужается.
2) ОДЗ расширяется.
3) при сужении ОДЗ.
4) при расширении ОДЗ. (Слайды 13, 14).
Коллективное обсуждение полученных результатов. Формулировка выводов.
Вывод: Некоторые формулы действий с логарифмами обладают тем свойством, что при их использовании О.Д.З. уравнения либо расширяется, либо – сужается. И если первую ситуацию легко исправить проверкой истинности равенства для найденных решений, то вторая ситуация совершенно недопустима, так как может привести к потере решений. (Слайд 15).
6. Диктант по свойствам логарифмической функции (Слайды 16-18).
| 1 | Логарифмическая функция у = logax определена при любом х | – |
| 2 | Функция у = logax определена при а > 0, а =/=1, х > 0 | + |
| 3 | Областью определения логарифмической функции является множество действительных чисел | – |
| 4 | Областью значений логарифмической функции является множество действительных чисел | + |
| 5 | Логарифмическая функция – четная | – |
| 6 | Логарифмическая функция – нечетная | – |
| 7 | Функция у = logax – возрастающая при а >1 | + |
| 8 | Функция у = logax при положительном, но меньшем единицы основании, – возрастающая | – |
| 9 | Логарифмическая функция имеет экстремум в точке (1; 0) | – |
| 10 | График функции у = log аx пересекается с осью ОХ | + |
| 11 | График логарифмической функции находится лишь в верхней полуплоскости | – |
| 12 | График логарифмической функции симметричен относительно ОХ | – |
| 13 | График логарифмической функции пересекает ОХ в точке (1; 0) | + |
| 14 | График логарифмической функции находится в 1 и 4 четвертях | + |
| 15 | Существует логарифм отрицательного числа | – |
| 16 | Существует логарифм дробного положительного числа | + |
| 17 | График логарифмической функции проходит через точку (0; 0) | – |
Виды логарифмических уравнени и способы их решения(Слайд 19).
1. Простейшие логарифмические уравнения: logax = b.
Решение данного вида уравнений следует из определения логарифма, т.е. х = а b и х > 0.
Т.к. основания одинаковые, то приравниваем выражения под логарифмами х = у , x > 0, y > 0 .
3. Уравнения квадратного вида log 2 ax + logax + c = 0.
Уравнения решаются способом введения новой переменной и переходом к обычному квадратному уравнению.
4. Уравнения вида a x = b
Решаются логарифмированием обеих частей по основанию а.
5. Уравнения, которые можно привести к простейшим, используя свойства логарифмов.
Строятся графики функций, расположенных в левой и правой частях уравнения и указывается корень уравнения.
7. Метод оценки границ.
Определяются границы значений всех функций, указанных в уравнении.
7. Самостоятельная работа (Слайд 20).
а) Решите уравнение log3(sinx – sin2x + 27) = 3
б) Найдите корни этого уравнения, принадлежащие отрезку
8. Логарифмический софизм 2>3 (Слайд 22).
Рассмотрим верное неравенство: 1/4 >1/8. Преобразуем его к виду: (1/2) 2 >(1/2) 3 , большему значению соответствует больший логарифм, значит: lg (1/2) 2 >lg(1/2) 3 .
По свойству логарифма: 2 lg(1/2)>3 lg(1/2). После сокращения на lg(1/2) имеем:2>3.
В чем состоит ошибка этого доказательства?
Ошибка в том, что при сокращении на lg1/2 не был изменен знак неравенства (> на
| Вид работы | Устная работа | Исследователь ская работа | Диктант | Самостоятель ная работа | Логарифмический софизм | Дополнительное задание | Итог |
| Мнение ученика | Можешь ли воспроизвести опорные знания? | Владеешь ли элементами исследования? | Можешь ли рассказать другим? | Все ли понятно? | Было ли интересно? | Было ли трудно? | Итоговое мнение |
– С какими трудностями вы встретились? (Слайд 30).
– Что помогло? (Опорные конспекты …)
– Что было сегодня необычного?
– Что понравилось?
– Что взяли с урока?
– Кому и в чем помог разобраться сегодняшний урок?
11. Итоги урока
1. Вычисление итогового количества баллов.
2. Самооценка своей работы на уроке.
3. Сдача листов самооценки. (Слайд 28)
заключение урока, я хочу вам прочитать высказывание: (Слайд 27).
Музыка может возвышать или умиротворять душу,
Живопись – радовать глаз,
Поэзия – пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать материальную сторону жизни людей,
А математика способна достичь всех этих целей».
Американский математик Морис Клайн.
Ода логарифму(Слайд 26)
| Сегодня тема: логарифмы. И это вам совсем не рифмы, Не повесть это, не рассказ, То – математика! Весь сказ! Что логарифмом называем? Так-так, так-так… Опять не знаем?! Кто «показатель» там сказал? Ну, молодец! Ты угадал! Чего, скажите, коль не трудно? Кто там шепнул: «О, как занудно»?! | Конечно, степени, друзья. Что возвести должна всё ж я? О, нет: не икс, не бэ, конечно. Перебирать что ль бесконечно? Так и урок пройдёт опять. Так кто же хочет всё же пять? «Я знаю! Это – основанье!», – Вдруг слышу гордое признанье. Внезапно зазвенел звонок… Ура! Закончился урок! |
12. Дополнительное задание
Сильные учащиеся, которые выполняют самостоятельную работу быстрее других, решают задания по карточкам. (Слайд 31).
Алгебра и начала математического анализа. 10 класс
Конспект урока
Алгебра и начала математического анализа, 10 класс
Урок № 24. Логарифм. Свойства логарифмов.
Перечень вопросов, рассматриваемых в теме
1. Определение логарифма.
2. Основное логарифмическое тождество.
3. Свойства логарифмов.
Глоссарий по теме
Логарифмом положительного числа 




Логарифмирование – это действие нахождения логарифма числа.
Основное логарифмическое тождество:
Свойства логарифмов. При 

— логарифм произведения: 
— логарифм частного: 
— логарифм степени: 
Колягин Ю. М., Ткачева М. В., Фёдорова Н.Е. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс. Базовый и углублённый уровни. – М.: Просвещение, 2014. – 384 с.
Открытые электронные ресурсы:
Теоретический материал для самостоятельного изучения
При решении простейших показательных уравнений не всегда можно найти точный ответ. Например, уравнение 




Абсцисса точки пересечения – единственное решение данного уравнения. Это число и называют логарифмом 5 по основанию 2.
Дадим определение логарифма.
Логарифмом положительного числа 




Т. е. логарифм числа 





1) 216 > 0; 2) 6 > 0, 6 ≠ 1; 3) 

1) 

Это действие называется логарифмированием.
Логарифмирование – это действие нахождения логарифма числа.
Существует краткая запись определения логарифма:
так называемое основное логарифмическое тождество. Его используют при вычислениях.


Решим несколько задач с использованием определения логарифма.
Задача 1. Вычислить 
Решение. Пусть 



Задача 2. Вычислить 
Решение. Для вычисления воспользуемся свойствами степеней: 1) 



Для решения более сложных задач потребуется знание свойств логарифмов. Рассмотрим их.
1. Логарифм произведения.
Логарифм произведения чисел 





2. Логарифм частного.
Логарифм частного чисел 





3. Логарифм степени.
Логарифм числа 




Важно! Свойства выполняются при 
Примеры и разбор решения заданий тренировочного модуля
№ 1. Вычислите: 
Чтобы выполнить это задание нам понадобятся следующие определения и свойства:
;
.
Представим 






Чтобы выполнить это задание нам понадобятся следующие определения и свойства:
;
;
;
.

http://urok.1sept.ru/articles/651739
http://resh.edu.ru/subject/lesson/5753/conspect/

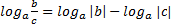
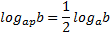
























 ;
; .
.



 ;
; ;
; ;
;

 .
.

