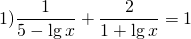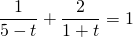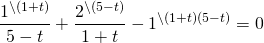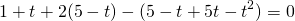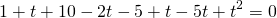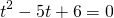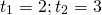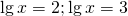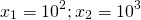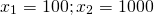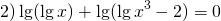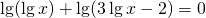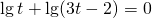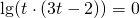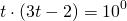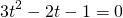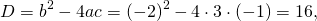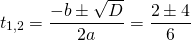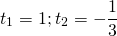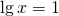План-конспект урока по теме: «Решение логарифмических уравнений методом замены переменной»
Разделы: Математика
Задача: опираясь на ранее изученные свойства логарифмов, научиться решать логарифмические уравнения с помощью замены переменной.
Цели:
- образовательная: научить применять метод замены переменной при решении логарифмических уравнений;
- развивающая: формировать приемы умственной деятельности: сравнения, аналогии, сопоставления, углублять и систематизировать знания по теме;
- воспитательная: учить преодолевать трудности, работать в быстром темпе, воспитывать стремление к совершенствованию знаний.
Тип урока: урок изучения нового.
Оборудование:
- плакаты: “Свойства логарифмов”, самостоятельная работа на два варианта;
- магнитная доска и магниты;
- карточки с домашним заданием.
Ход урока
1. Организационный момент.
Вступительное слово учителя. Сегодня я хочу познакомить вас с одним из интересных способов решения логарифмических уравнений – методом замены переменной. При их решении мы будем пользоваться свойствами логарифмов, которые приведены на плакате.
2. Объяснение нового материала. Рассмотрим примеры.
Пусть log9(x-2)=t , тогда x-2=9 t и исходное уравнение
t+
=1,5
1,5t=1,5
t=1 , отсюда x-2=9 1
x=11
Решите в группах уравнение:
Log4 x (5-x)+log8 x (5-x)+log16 x (5-x)=
Log4 x (5-x)=t, заменить 5-x на (4 x ) 
Применяя формулу перехода к другому основанию: log3x=
И полагая, что log2x=t; x>0, имеем
t+
=t*
, т.к.
= log32, то
t+tlog32-t 2 log32=0.
t(1+log32-t log32)=0, откуда
t=0 или tlog32= log32+ log33
tlog32= log36
t=
log2x=0 log2x= log26
x=2 0 =1 x=6
Решите в группах уравнение:
(ответ: 
Положим log2х=t; x>0, тогда х=2 t



t(2+t)+(2t+1)(t+1)=1,5(t+1)(2+t)
t 2 +2t+2t 2 +3t+1=1,5t 2 +4,5t+3
1,5t 2 +0,5t-2=0
t1=1 t2=
x=2 1 =2 x=2 4/3 =
Ответ: 2 и
Решите в группах:
Logх2*
=
Пример 4. Некоторые уравнения можно решить логарифмированием обеих частей уравнения, но можно и при помощи замены переменной. Рассмотрим как раз такой случай.
log2x=t, x>0; x=2 t

t 2 +3t-4=0
t1=1; t2=-4 отсюда x=2 1 =2
x=2 -4 =
Ответ: 2 и
Решите в группах следующее уравнение:
log6x=t, x>0; x=6 t

t 2 =1 t=1 и t=-1,
тогда x=6 и x=
Ответ: 6 и
В группах решите:
(ответ: 
1 вариант 2 вариант а) log2x+ log4x+ log8x=11 а) log4x+ log16x+ log2x=7 б) x 2lgx =10x б) x 2lgx =100x в) в) г) г) д) д) е) 3log3xx=2log9xx 2 е) 2log4xx 3 =5log2xx
а)

б) log4x+logx8=
в)
г)
д)
е)
Список использованной литературы
- Башмаков М.И., Братусь Т.А., Жарковская Н.А. и др. “Алгебра и начала анализа. Дидактические материалы. 10-11 классы” М., Дрофа, 2004.
- Бородуля И.Т. “Показательная и логарифмическая функции (задачи и упражнения)” М., Просвещение,1984.
- Зив Б.Г., Алтынов П.И. “Алгебра и начала анализа. Геометрия. Дидактические материалы” М., Дрофа, 1999.
- Зив Б.Г., Гольдич В.А. “Алгебра и начала анализа. Дидактические материалы” СПб.,Петроглиф, 2006.
- Карп А.П. “Сборник задач по алгебре и началам анализа” М., Просвещение, 1999.
- Саакян С.М., Гольдман А.М., Денисов Д.В. “Задачи по алгебре и началам анализа” М., Просвещение, 1997.
- Чулков П.В. “Уравнения и неравенства в школьном курсе математики” М., Педагогический университет “Первое сентября”, 2006.
- Шабунин М.В. “ Уравнения. Лекции для старшеклассников и абитуриентов” М., Чистые пруды, 2005.
- Шарыгин И.Ф., Голубев В.И. “Факультативный курс по математике. Решение задач. 11 класс” М., Просвещение, 1991.
Алгебра
План урока:
Задание. Укажите корень логарифмического уравнения
Задание. Решите урав-ние
В чуть более сложных случаях под знаком логарифма может стоять не сама переменная х, а выражение с переменной. То есть урав-ние имеет вид
Задание. Найдите решение логарифмического уравнения
Задание. Решите урав-ние
Задание. Решите урав-ние
Получили показательное уравнение. Показатели степеней можно приравнять, если равны их основания:
Уравнения вида logaf(x) = logag(x)
Порою логарифм стоит в обеих частях равенства, то есть и слева, и справа от знака «равно». Если основания логарифмов совпадают, то должны совпадать и аргументы логарифмов.
Задание. Решите урав-ние
Задание. Найдите корень урав-ния
Ситуация несколько усложняется в том случае, когда, под знаком логарифма в обоих частях равенства стоят выражения с переменными, то есть оно имеет вид
С одной стороны, очевидно, что должно выполняться равенство f(x) = g(x). Но этого мало, ведь под знаком логарифма не должно стоять отрицательное число. Поэтому после получения корней следует подставить их в урав-ние и убедиться, что они не являются посторонними корнями.
Задание. Решите урав-ние
Получили квадратное уравнение, которое решаем с помощью дискриминанта:
Получили два корня, (– 3) и 4. Однако теперь подставим их в исходное урав-ние и посмотрим, что у нас получится. При х = – 3 имеем:
Это верное равенство, поэтому х = – 3 действительно является корнем урав-ния. Теперь проверяем х = 4:
Хотя выражения и справа, и слева одинаковы, равенство верным считать нельзя, ведь выражение log3 (– 1) не имеет смысла! Действительно, нельзя вычислять логарифм от отрицательного числа. Поэтому корень х = 4 оказывается посторонним, и у нас остается только один настоящий корень – число (– 3).
Уравнения, требующие предварительных преобразований
Естественно, не всегда в обоих частях логарифмических уравнений и неравенств стоят только логарифмы с совпадающими основаниями. Часто требуется выполнить некоторые предварительные преобразования, чтобы привести урав-ние к виду logaf(x) = logag(x).
Задание. Решите урав-ние
с помощью которой любой множитель можно внести под знак логарифма. Сделаем это и в нашем случае:
Теперь в обеих частях равенства не стоит ничего, кроме логарифмов с одинаковыми основаниями. Поэтому мы можем приравнять их аргументы:
Задание. Решите урав-ние
Снова проверяем каждый из корней, подставляя его в исходное ур-ние. Прих = –1 получаем
Задание. Решите урав-ние
Решение. В правой части снова стоит сумма, но на этот раз не логарифмов. Однако число 1 можно представить как log5 5. Тогда урав-ние можно преобразовать:
Задание. Решите урав-ние
Решение. Данный пример похож на простейшее логарифмическое уравнение, однако переменная находится в основании логарифма, а не в аргументе. По определению логарифма мы можем записать, что
Первый вариант придется отбросить, так как основание логарифма, (а в данном случае это выражение х – 5) не может быть отрицательным числом. Получается, что
Задание. Решите урав-ние
Решение. Здесь ситуация осложняется тем, что основания логарифмов разные. Поэтому один из них необходимо привести к новому основанию. Попробуем привести log25x 4 к основанию 5, используя известную нам формулу
Мы добились того, что у логарифмов одинаковые основания, а потому мы можем приравнять их аргументы:
Логарифмические уравнения с заменой переменных
Иногда приходится делать некоторые замены, чтобы уравнение приняло более привычный вид.
Задание. Решите уравнение методом замены переменной
Задание. Найдите решение уравнения методом замены переменной
Решение. Для начала напомним, что символ lg означает десятичный логарифм. Отдельно знаменатель дроби в правой части:
Логарифмирование уравнений
Ясно, что если от равных величин взять логарифмы по одному и тому же основанию, то тогда эти логарифмы окажутся также равными. Если подобный прием применяют при решении урав-ния, то, говорят, что производится логарифмирование уравнения. Иногда оно позволяет решить некоторые особо сложные примеры.
Задание. Укажите корни урав-ния
Здесь переменная величина находится одновременно и в основании степени, и в ее показателе. Возьмем от правой и левой части урав-ния логарифм по основанию 5:
Возвращаемся от переменной t к переменной х:
Переход от логарифмических неравенств к нелогарифмическим
Рассмотрим график логарифмической функции у = logax при условии а > 1. Она является возрастающей функцией. Если на оси Ох отложить два числа tи s так, чтобы t располагалось левее s (то есть t 1). Но это не совсем так. Дело в том, что надо учесть ещё и тот факт, что под знаком логарифма может стоять исключительно положительное число. Получается, что от простейшего логарифмического неравенства
Естественно, вместо величин t и s могут стоять как числа, так и выражения с переменными.
Задание. Найдите решение логарифмического неравенства
Ответ можно оставить и в такой форме, однако всё же принято записывать его в виде промежутка. Очевидно, что нерав-во 0 logas:
Но, снова-таки, мы должны учесть, числа t может быть лишь положительным (тогда s, которое больше t, автоматически также окажется положительным). Получается, что при 0 loga s можно перейти к двойному нерав-ву 0 2 – 45х + 200 имеет решение
Однако в системе (5) есть ещё два неравенства, х > 0 и 45 >x. Их решениями являются промежутки (0; + ∞) и (– ∞; 45). Чтобы определить решение всей системы, отметим на одной прямой решения каждого отдельного нерав-ва и найдем область их пересечения:
Видно, что решениями нерав-ва будут являться промежутки (0; 5) и (40; 45), на которых справедливы все три нерав-ва, входящих в систему (5).
Замена переменной в логарифмических уравнениях
Замена переменной в логарифмических уравнениях в ряде случаев позволяет упростить решение. Самый распространённый пример введения вспомогательной переменной — логарифмические уравнения, сводящиеся к квадратным — мы уже рассмотрели.
Замена переменной в уравнении, содержащем логарифмы в знаменателе, даёт возможность от логарифмического уравнения перейти к дробному рациональному.
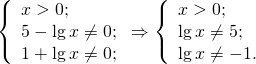
Пусть lgx=t, t≠5, t≠-1. Тогда имеем дробное рациональное уравнение
Возвращаемся к исходной переменной
В следующем примере замена переменной не столь очевидна.
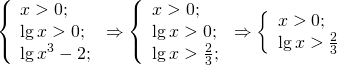
(достаточно довести нахождение ОДЗ до этого момента).
После вынесения показателя степени за знак логарифма
удобно ввести новую переменную: пусть lgx=t, t>2/3. Имеем:
Сумма логарифмов равна логарифму произведения
Отсюда, по определению логарифма,
Второй корень не удовлетворяет условию t>2/3.
Выполняем обратную замену:
Замена переменной также используется при логарифмировании. Этот способ решения логарифмических уравнений мы рассмотрим позже.
http://100urokov.ru/predmety/urok-9-uravneniya-logarifmicheskie
http://www.logarifmy.ru/zamena-peremennoj-v-logarifmicheskix-uravneniyax/
 =1,5
=1,5 

 =t*
=t* , т.к.
, т.к.  = log32, то
= log32, то 






 =
=
 log2x=t, x>0; x=2 t
log2x=t, x>0; x=2 t 



 log6x=t, x>0; x=6 t
log6x=t, x>0; x=6 t 
 t 2 =1 t=1 и t=-1,
t 2 =1 t=1 и t=-1,