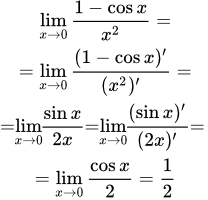Правило Лопиталя: теория и примеры решений
Правило Лопиталя и раскрытие неопределённостей
Производная от функции недалеко падает, а в случае правил Лопиталя она падает точно туда же, куда падает исходная функция. Это обстоятельство помогает в раскрытии неопределённостей вида 0/0 или ∞/∞ и некоторых других неопределённостей, возникающих при вычислении предела отношения двух бесконечно малых или бесконечно больших функций. Вычисление значительно упрощается с помощью этого правила (на самом деле двух правил и замечаний к ним):

Как показывает формула выше, при вычислении предела отношений двух бесконечно малых или бесконечно больших функций предел отношения двух функций можно заменить пределом отношения их производных и, таким образом, получить определённный результат.
Перейдём к более точным формулировкам правил Лопиталя.
Правило Лопиталя для случая предела двух бесконечно малых величин. Пусть функции f(x) и g(x) имеют производные (то есть дифференцируемы) в некоторой окрестности точки a. А в самой точке a они могут и не иметь производных. При этом в окрестности точки a производная функции g(x) не равна нулю ( g‘(x)≠0 ) и пределы этих функций при стремлении икса к значению функции в точке a равны между собой и равны нулю:

Тогда предел отношения этих функций равен пределу отношения их производных:

Правило Лопиталя для случая предела двух бесконечно больших величин. Пусть функции f(x) и g(x) имеют производные (то есть дифференцируемы) в некоторой окрестности точки a. А в самой точке a они могут и не иметь производных. При этом в окрестности точки a производная функции g(x) не равна нулю ( g‘(x)≠0 ) и пределы этих функций при стремлении икса к значению функции в точке a равны между собой и равны бесконечности:

Тогда предел отношения этих функций равен пределу отношения их производных:

Иными словами, для неопределённостей вида 0/0 или ∞/∞ предел отношения двух функций равен пределу отношения их производных, если последний существует (конечный, то есть равный определённому числу, или бесконечный, то есть равный бесконечности).
Замечания.
1. Правила Лопиталя применимы и тогда, когда функции f(x) и g(x) не определены при x = a.
2. Если при вычисления предела отношения производных функций f(x) и g(x) снова приходим к неопределённости вида 0/0 или ∞/∞, то правила Лопиталя следует применять многократно (минимум дважды).
3. Правила Лопиталя применимы и тогда, когда аргумент функций (икс) стремится не к конечному числу a, а к бесконечности (x → ∞).
К неопределённостям видов 0/0 и ∞/∞ могут быть сведены и неопределённости других видов.
Раскрытие неопределённостей видов «ноль делить на ноль» и «бесконечность делить на бесконечность»
Пример 1. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
Решение. Подстановка в заданную функцию значения x=2 приводит к неопределённости вида 0/0. Поэтому производную каждой функции и получаем
В числителе вычисляли производную многочлена (применяя для этого формулы 1, 2 и 3 из таблицы производных), а в знаменателе — производную сложной логарифмической функции. Перед последним знаком равенства вычисляли обычный предел, подставляя вместо икса двойку.
Пример 2. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:

Решение. Подстановка в заданную функцию значения x=0 приводит к неопределённости вида 0/0. Поэтому вычисляем производные функций в числителе и знаменателе и получаем:
Пример 3. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:

Решение. Подстановка в заданную функцию значения x=0 приводит к неопределённости вида 0/0. Поэтому вычисляем производные функций в числителе и знаменателе и получаем:
Пример 4. Вычислить

Решение. Подстановка в заданную функцию значения икса, равного плюс бесконечности, приводит к неопределённости вида ∞/∞. Поэтому применим правило Лопиталя:
Замечание. Переходим к примерам, в которых правило Лопиталя приходится применять дважды, то есть приходить к пределу отношений вторых производных, так как предел отношения первых производных представляет собой неопределённость вида 0/0 или ∞/∞.
Пример 5. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:

Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных дают неопределённость вида ∞/∞.
Пример 6. Вычислить

Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных дают неопределённость вида 0/0.
Пример 7. Вычислить

Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных сначала дают неопределённость вида — ∞/∞, а затем неопределённость вида 0/0.
Пример 8. Вычислить

Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных сначала дают неопределённость вида ∞/∞, а затем неопределённость вида 0/0.
Применить правило Лопиталя самостоятельно, а затем посмотреть решение
Пример 9. Вычислить

Подсказка. Здесь придётся попыхтеть несколько больше обычного над преобразованием выражений под знаком предела.
Пример 10. Вычислить

Подсказка. Здесь правило Лопиталя придётся применять трижды.
Раскрытие неопределённостей вида «ноль умножить на бесконечность»
Пример 11. Вычислить

(здесь неопределённость вида 0∙∞ мы преобразовали к виду ∞/∞, так как
а затем применили правила Лопиталя).
Пример 12. Вычислить

В этом примере использовано тригонометрическое тождество 
Раскрытие неопределённостей видов «ноль в степени ноль», «бесконечность в степени ноль» и «один в степени бесконечность»
Неопределённости вида 


Чтобы вычислить предел выражения 



Используя логарифмическое тождество и свойство непрерывности функции (для перехода за знак предела), предел следует вычислять следующим образом:
Отдельно следует находить предел выражения в показателе степени и возводить e в найденную степень.
Пример 13. Вычислить, пользуясь правилом Лопиталя

Вычисляем предел выражения в показателе степени


Пример 14. Вычислить, пользуясь правилом Лопиталя

Вычисляем предел выражения в показателе степени


Пример 15. Вычислить, пользуясь правилом Лопиталя

Вычисляем предел выражения в показателе степени

Раскрытие неопределённостей вида «бесконечность минус бесконечность»
Это случаи, когда вычисление предела разности функций приводит к неопределённости «бесконечность минус бесконечность»: 
Вычисление такого предела по правилу Лопиталя в общем виде выглядит следующим образом:
В результате таких преобразований часто получаются сложные выражения, поэтому целесообразно использовать такие преобразования разности функций, как приведение к общему знаменателю, умножение и деление на одно и то же число, использование тригонометрических тождеств и т.д.
Пример 16. Вычислить, пользуясь правилом Лопиталя

Решение. Пользуясь вышеперечисленными рекомендациями, получаем
Пример 17. Вычислить, пользуясь правилом Лопиталя

Решение. Пользуясь вышеперечисленными рекомендациями, получаем
Решение пределов функций, используя правило Лопиталя
Метод решения
Одним из самых мощных методов раскрытия неопределенностей и вычисления пределов функций является использование правила Лопиталя. Оно позволяет раскрывать неопределенности вида 0/0 или ∞/∞ в конечной или бесконечно удаленной точке, которую мы обозначим как x 0 . Правило Лопиталя заключается в том, что мы находим производные числителя и знаменателя дроби. Если существует предел , то существует равный ему предел .
Если после дифференцирования мы опять получаем неопределенность, то процесс можно повторить, то есть применить правило Лопиталя уже к пределу . И так далее, до раскрытия неопределенности.
Для применения этого правила, должна существовать такая проколотая окрестность точки x 0 , на которой функции в числителе и знаменателе являются дифференцируемыми и функция в знаменателе и ее производная не обращается в нуль.
Применение правила Лопиталя состоит из следующих шагов.
1) Приводим неопределенность к виду 0/0 или ∞/∞ . Для этого, если требуется, выполняем преобразования и делаем замену переменной. В результате получаем предел вида .
2) Убеждаемся, что существует такая проколотая окрестность точки x 0 , на которой функции в числителе и знаменателе являются дифференцируемыми и знаменатель и его производная не обращаются в нуль.
3) Находим производные числителя и знаменателя.
4) Если имеется конечный или бесконечный предел , то задача решена: .
5) Если предела не существует, то это не означает, что не существует исходного предела. Это означает, что данную задачу решить с помощью правила Лопиталя нельзя. Нужно применить другой метод (см. пример ниже).
6) Если в пределе вновь возникает неопределенность, то к нему также можно применить правило Лопиталя, начиная с пункта 2).
Как указывалось выше, применение правила Лопиталя может привести к функции, предела которой не существует. Однако это не означает, что не существует исходного предела. Рассмотрим следующий пример.
.
Применяем правило Лопиталя. , .
Однако предела не существует. Не смотря на это, исходная функция имеет предел:
.
Правило Лопиталя. Формулировки теорем
Здесь мы приводим формулировки теорем, на которых основывается раскрытие неопределенностей по правилу Лопиталя.
Теорема о раскрытии неопределенности 0/0
Пусть функции f и g имеют производные в проколотой (двусторонней или односторонней) окрестности конечной или бесконечно удаленной ( ) точки , причем и не равны нулю в этой окрестности. И пусть
.
Тогда, если существует конечный или бесконечный предел
,
то существует равный ему предел
.
Здесь для двусторонней окрестности. Для односторонней окрестности, , или .
Теорема о раскрытии неопределенности ∞/∞
Пусть функции f и g имеют производные в проколотой (двусторонней или односторонней) окрестности конечной или бесконечно удаленной ( ) точки , причем не равна нулю в этой окрестности. И пусть
.
Тогда, если существует конечный или бесконечный предел
,
то существует равный ему предел
.
Здесь для двусторонней окрестности. Для односторонней окрестности, , или .
Примеры
Все примеры Далее мы приводим подробные решения следующих пределов с помощью правила Лопиталя.
⇓, ⇓, ⇓,
⇓, ⇓, ⇓.
Пример 1
Все примеры ⇑ Показать, что экспонента растет быстрее любой степенной функции, а логарифм – медленнее. То есть показать, что
А) ;
Б) ,
где .
Рассмотрим предел А). При . Это неопределенность вида . Для ее раскрытия применим правило Лопиталя. Пусть
.
Находим производные. . Тогда
.
Если , то неопределенность исчезает, поскольку при . По правилу Лопиталя,
.
Если , то применяем правило Лопиталя n раз, где – целая часть числа b .
;
.
Поскольку , то . Хотя мы привыкли читать слева направо, но эту серию равенств следует читать справа налево следующим образом. Поскольку существует предел , то существует равный ему предел . Поскольку существует предел , то существует равный ему предел . И так далее, пока не дойдем до предела .
Теперь рассмотрим предел Б):
. Сделаем замену переменной . Тогда ; при ; .
Пример 2
Все примеры ⇑ Найти предел с помощью правила Лопиталя:
.
Это неопределенность вида 0/0 . Находим по правилу Лопиталя.
.
Здесь, после первого применения правила мы снова получили неопределенность. Поэтому применили правило Лопиталя второй раз. Эту серию равенств нужно читать справа налево следующим образом. Поскольку существует предел , то существует равный ему предел . Поскольку существует предел , то существует равный ему исходный предел .
Пример 3
Все примеры ⇑ Вычислить предел, используя правило Лопиталя.
.
Найдем значения числителя и знаменателя при :
;
.
Числитель и знаменатель равны нулю. Мы имеем неопределенность вида 0/0 . Для ее раскрытия, применим правило Лопиталя.
Пример 4
Все примеры ⇑ Решить предел с помощью правила Лопиталя.
.
Здесь мы имеем неопределенность вида (+0) +0 . Преобразуем ее к виду +∞/+∞ . Для этого выполняем преобразования.
.
Находим предел в показателе степени, применяя правило Лопиталя.
.
Поскольку экспонента – непрерывная функция для всех значений аргумента, то
.
Пример 5
Все примеры ⇑ Найти предел используя правило Лопиталя:
.
Здесь мы имеем неопределенность вида ∞ – ∞ . Приводя дроби к общему знаменателю, приведем ее к неопределенности вида 0/0 :
.
Применяем правило Лопиталя.
;
;
.
Здесь у нас снова неопределенность вида 0/0 . Применяем правило Лопиталя еще раз.
;
;
.
Окончательно имеем:
.
Как и во всех пределах, вычисляемых с помощью правила Лопиталя, читать нужно с конца. Поскольку существует предел , то существует равный ему предел . Поскольку существует предел , то существует равный ему исходный предел .
Примечание. Можно упростить вычисления, если воспользоваться теоремой о замене функций эквивалентными в пределе частного. Согласно этой теореме, если функция является дробью или произведением множителей, то множители можно заменить на эквивалентные функции. Поскольку при , то
.
Использованная литература:
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, 2003.
Автор: Олег Одинцов . Опубликовано: 05-05-2019
Лопиталь уравнения и их решения
Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!
Контакты
 |