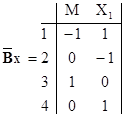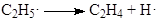Максимальный базис итоговых уравнений реакций

Приближения квазистационарности и квазиравновесия

Формально – кинетический анализ гипотез

Кинетический анализ гипотез – важный этап рациональной стратегии, предшествующий планированию кинетического эксперимента с целью дискриминации гипотез. Каждую гипотезу необходимо проанализировать с учётом различных сочетаний быстрых и медленных стадий (приближения квазистационарности, квазиравновесия, возможных лимитирующих стадий), с учётом различной структуры материальных балансов по катализатору, а также природы поверхности в случае гетерогенных катализаторов и состояния комплексов в растворе в случае гомогенного катализа комплексами металлов.

Стехиометрический анализ механизмов.

Теория маршрутов

Первый этап формально-кинетического анализа гипотез о механизме – стехиометрический анализ механизмов. Основой такого анализа является теория маршрутов Хориути-Тёмкина. Важность теории (или метода) маршрутов, позволяющей найти итоговые уравнения реакций, исходя из механизма процесса, а не только на основе материального баланса, видна из следующего примера.

Пример 1. Материальный баланс процесса описывается уравнением (1), а схема механизма – уравнениями (2 – 3):

(1)

(2)

(3)

(4)

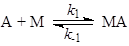
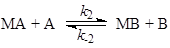
где М – катализатор, МА и МВ – промежуточные вещества.

Если сложить стадии механизма (для стационарных или квазистационарных режимов), промежуточные вещества и катализатор исчезают и получается итоговое уравнение

(5)

С позиций стехиометрии и материального баланса уравнения (1) и (5) линейно зависимы. С позиций кинетических скорость реакции превращения А в В есть скорость по итоговому уравнению (5) и именно эта скорость R, как разность скоростей в прямом (R + ) и обратном (R – ) направлениях (R = R + – R – ) соответствует механизму (2 – 4). При [А], [В] >> [М]_Σ и [М]_Σ >> [МА], [МВ] ([М]_Σ @ [М]) получаем для стационарного или квазистационарного режимов

(6)

При равновесии (R + = R – ) из (6) получается константа равновесия реакции (5) К = [А] 2 / [В] 2 . Если возникает задача найти скорость прямой реакции, используя скорость обратной реакции и соотношение (7)

, (7)

где DG – изменение изобарно-изотермического (химического) потенциала для итогового уравнения в ходе реакции, то для записи DG также следует использовать уравнение, вытекающее из механизма, в данном случае, уравнение (5). Соотношение (7) справедливо только для одномаршрутных реакций.

Напомним определения маршрута реакции. Маршрутом реакции называется такая последовательность стадий, входящих в механизм сложной реакции, которая при сложении уравнений стадий, умноженных на особые стехиометрические числа стадий ν_j, даёт итоговое уравнение, не содержащее промежуточных веществ (интермедиатов) – важнейших участников механизма сложной реакции.

Маршрутом реакции называется также и вектор, компонентами которого являются стехиометрические числа стадий ν_j. Для механизма (2 – 4) таким вектором являются набор из трёх компонент ν₂ = 1, ν₃ = 1, ν₄ = 1: = (1, 1, 1). Другой набор стехиометрических чисел = (0.5, 0.5, 0.5) даёт уравнение А = В, но как мы видели выше, такое итоговое уравнение противоречит кинетике стационарного процесса.

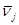
Число линейно-независимых маршрутов определяется по уравнению Хориути (8)

где I – общее число интермедиатов, W – число независимых линейных законов сохранения (число линейных связей между интермедиатами) N_I = I – W. Очевидно, что N_I = rank B_X, где B_X – матрица стехиометрических коэффициентов для интермедиатов (B_X – блок стехиометрической матрицы механизма В_М).

Для каталитических реакций с одним типом катализатора (или активных центров) W = 1, т.е. имеется один стехиометрический закон сохранения – материальный баланс по катализатору. В случае двух катализаторов, участвующих в механизме реакции, W = 2.

Для нахождения векторов стехиометрических чисел ,т.е. матрицы Г, решается система уравнений

(9)

Для решения системы (9) используем только линейно-независимые столбцы матрицы В_Х и один вектор из матрицы Г. Например, для двухмаршрутного каталитического процесса с катализатором М и первым интермедиатом Х₁ имеем матрицу В_Х (rank B_X = 2) S = 4 и вектор .

Получим 2 уравнения:

(10)

Для решения системы двух уравнений с четырьмя неизвестными разделим переменные на независимые, значения которых задаём, и зависимые

. (11)

При таком разделении системы уравнений следует проверить, чтобы определитель левой части D ≠ 0, иначе система не будет иметь решения. Для удобства нахождения значений ν₁ и ν₂ (при заданных ν₃ и ν₄), систему (11) приводят к единичному базису (метод Жордано-Гаусса) так, чтобы каждое уравнение слева имело одно неизвестное. Так, сложив уравнения в системе (11), получим ν₂ = ν₃ + ν₄ и система (11) примет вид (12)

(12)

Задавая ν₃ = 1 и ν₄ = 0, получим ν₁ = 1 и ν₂ = 1, т.е. для первого маршрута. При ν₃ = 0 и ν₄ = 1 ν₁ = 0 и ν₂ = 1 и для второго маршрута. При ν₃ = 0 и ν₄ = 0 все решения будут нулевыми.

Пример 2. Рассмотрим пример нелинейного механизма.

(13)

Здесь одно линейно-независимое промежуточное соединение Х (N_I = 1), 2 стадии (S = 2) и один маршрут Р = 2 – 1 = 1. Матрицу стехиометрических коэффициентов интермедиатов В_Х запишем вектором-строкой . Поскольку , умножим вектор-строку на вектор столбец . Получим одно уравнение

которое имеет одно линейно-независимое решение. Задав ν₁ = 1, получим ν₂ = 0.5. При ν₁ = 2 ν₂ = 1 и т.д. Если при сложении стадий (1) и (2) (для исключения Х из итогового уравнения) умножим стадии (1) и (2) на наборы |1 0.5| или |2 1|, получим итоговые уравнения, соответственно, маршрутов N (1) и N (2) :

Очевидно, что ΔG (Р) (по маршруту N (Р) ) определяется уравнением (15)

(15)

В соответствии с уравнением (7) для ΔG (Р) и для ΔG_j получаем:

(16)

где –скорости элементарной стадии в прямом и обратном направлениях.

Для маршрута N (1) :

(17)

Для маршрута N (2) :

(18)

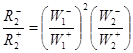
Примем стадию (1) механизма (13) в качестве лимитирующей, а стадию (2) – квазиравновесной ( ). Тогда при равновесии брутто-процесса ( ) получим из уравнения (17) константу равновесия итогового уравнения для маршрута N (1)

,

а из уравнения (18) – константу равновесия маршрута N (2)

.

Такие уравнения для К (1) и К (2) получим и в случае лимитирующей второй стадии.

Если кинетические уравнения получены экспериментально, итоговые уравнения выбираются уже не произвольно. Так, например, для механизма (13), если R + µ [A] (стадия (1) лимитирующая), итоговое уравнение, которое получится при равновесии, будет уравнением N (1) . Если R + µ [A] 2 , итоговое уравнение N (2) . Поэтому для определения скорости R — по известной R + (и наоборот) следует использовать соответствующие кинетике итоговые уравнения. Таким образом, кинетика реакции в случае нелинейного механизма может ограничивать выбор маршрута.

Для обратимых стационарных и квазистационарных процессов с линейными механизмами нет ограничений при выборе базиса маршрутов и итоговых уравнений.. Однако итоговое уравнение, как мы видели в случае 2А = 2В, не должно противоречить кинетическому уравнению, следующему из механизма реакции. Для механизмов с необратимыми стадиями формально также можно использовать любые наборы , включая и отрицательные ν_j для необратимых стадий. Вместе с тем, в согласии с физическим смыслом целесообразно выбирать такие базисы маршрутов, чтобы и маршрут и скорость по маршруту относились к термодинамически и кинетически разрешенному направлению реакции (направление необратимых стадий).

Для нелинейных одномаршрутных механизмов, имеющих лимитирующую стадию, можно получить выражения для скорости лимитирующей стадии в прямом и обратном направлениях, но в этом случае выбор итогового уравнения будет определяться природой лимитирующей стадии.

Получив матрицу Г, найдём итоговое уравнение, т.е. матрицу стехиометрических коэффициентов итоговых уравнений В_Р,

или

и уравнения, связывающие скорости по веществу R_N и скорости по маршруту R_P

.

Поскольку , получим или . Домножив обе части полученного матричного уравнения слева на В_N, получим уравнение (19)

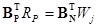
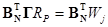
называемое условием стационарности стадий Хориути — Тёмкина. Это уравнение устанавливает связь между скоростью стадии и скоростью по маршруту и показывает, как стадии механизма перераспределяются по маршрутам. Кроме того, уравнение (19) можно использовать и для вывода уравнений для скоростей R_i и R_P (аналогично методу Боденштейна), поскольку система (19) содержит S уравнений и S неизвестных (S = N_I + P). Условие стационарности стадий (19) эквивалентно условию Боденштейна

. (20)

Из (20) и (19) получаем уравнение (9), используемое для нахождения базиса маршрутов

.

Пример 3. Механизм гидрирования этилена (21) на поверхности твердого металлического катализатора опишем последовательностью четырех элементарных стадий:

(21)

N_I = rankB_X = 2 (есть один закон сохранения, ). Следовательно, P = S – N_I = 2. Найдем матрицу Г. Для этого запишем систему уравнений . Возьмем два независимых столбца (Z, ZH₂) (см. уравнения (10 – (12))

Задавая n₃ и n₄, получим два вектора n_j для двух маршрутов, т.е. матрицу Г:

Итоговые уравнения для обоих маршрутов одинаковы

Поскольку стадия механизма (4) обратима, можно взять другую комбинацию маршрутов:

Получим другую матрицу B_P:

и новые итоговые уравнения:

Второй маршрут (II * ) называют пустым маршрутом. Скорость реакции по пустому маршруту не равна нулю. Это скорость перехода интермедиатов:

по циклической последовательности стадий. Скорости , , по пустому маршруту равны нулям. , , .

Ранг матрицы B_P, т.е. базис Q_P итоговых уравнений, для маршрутов I и II равен 1 (Q_P = rankB_P = 1). Во втором случае (I и II * ) число ненулевых итоговых уравнений равно Q_P. Такой базис маршрутов называется “стехиометрическим базисом” маршрутов (число пустых маршрутов равно P – Q_P).

На данном множестве реагентов и продуктов мы имеем максимальный базис итоговых (брутто) реакций по стехиометрическому правилу Гиббса

, (22)

где N – общее число участников, Н – атомная матрица. Сравнение Q_max с базисом итоговых уравнений маршрутов Q_P дает неравенство:

В рассмотренном выше примере №1 Q_max = 1, Q_P = 1, Р = 2.

Пример 4. Рассмотрим более сложный случай пятистадийного цепного процесса пиролиза этана.

(1)

(2)

(3)

(4)

(5)

Произведение дает три уравнения:

Возьмем n₄ и n₅ в качестве независимых переменных и преобразуем систему уравнений:

Определитель левой части D ¹ 0. Задавая n₄ = 1, n₅ = 0 и n₄ = 0, n₅ = 1, получаем матрицу Г для Р = 2 и матрицу B_P:

Приближения квазистационарности и квазиравновесия

При выводе кинетических уравнений часто используют различные допущения о соотношениях скоростей стадий, поскольку скорости элементарных стадий могут сильно различаться по величине. Например, скорости стадий адсорбции и химических превращений на поверхности катализатора. Важное допущение – о наличии медленных и быстрых стадий. Быстрые обратимые стадии являются квазиравновесными (РЕ – preequilibrium), а допущение о наличии таких стадий – приближением квазиравновесия. В закрытых системах особенно для каталитических реакций используют допущение о квазистационарности концентраций интермедиатов (SS – steady — state, допущение Боденштейна). Критерии применимости этих допущений рассмотрены в учебном пособии О.Н. Тёмкина, К.Ю. Одинцова и Л.Г. Брука “Приближения квазистационарности и квазиравновесия в химической кинетике”, М., МИТХТ, 2001г. Здесь приведем условия реализации различных приближений для простой схемы:

(24)

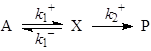
Необходимым и достаточным условием реализации приближения Боденштейна (SS) является условие С_Х >k₁>>k_-1>1SSIIk₂>>k—₁>>k₁>1SSIIIk₁>>k₂>>k_-1>>1*IVk₁>>k—₁>>k₂>>1>k₂>>k₁>k₁>>k₂>k₁, k_-1 (I, II) и k—₁>>k₁ (V, VI), делающие ε₁ * ( ε₂ > k₁ ≈ k—₁> 1SSVIIIk₁ ≈ k—₁k₂ >> k₁ ≈ k—₁≈ 1> 1*XIk₁ ≈ k₂k_-1 >> k₁ ≈ k₂

При близости констант k₂ и k—₁ также, как и в варианте III, режим не является строго квазиравновесным (соотношение С_Х / С_А = α не постоянно в ходе процесса). При равенстве k₁ = k₂ достигается режим квазистационарности в условиях квазиравновесия. Таким образом, приближение SS выполняется:

Приближение РЕ выполняется:

Экспериментальными критериями режима SS являются следующие:

3) В случае гомогенных каталитических реакций при 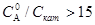ошибка SS-приближения не превышает 1%.

4) В гетерогенном катализе в закрытой и открытой системах количество молей вещества в газе ( ) должно быть больше количества вещества на поверхности ( ):

.

В этом случае

Формально–кинетический анализ гипотез (стр. 2 из 3)

Если кинетические уравнения получены экспериментально, итоговые уравнения выбираются уже не произвольно. Так, например, для механизма (13), если R + µ [A] (стадия (1) лимитирующая), итоговое уравнение, которое получится при равновесии, будет уравнением N (1) . Если R + µ [A] 2 , итоговое уравнение N (2) . Поэтому для определения скорости R — по известной R + (и наоборот) следует использовать соответствующие кинетике итоговые уравнения. Таким образом, кинетика реакции в случае нелинейного механизма может ограничивать выбор маршрута.

Для обратимых стационарных и квазистационарных процессов с линейными механизмами нет ограничений при выборе базиса маршрутов и итоговых уравнений.. Однако итоговое уравнение, как мы видели в случае 2А = 2В, не должно противоречить кинетическому уравнению, следующему из механизма реакции. Для механизмов с необратимыми стадиями формально также можно использовать любые наборы

Для нелинейных одномаршрутных механизмов, имеющих лимитирующую стадию, можно получить выражения для скорости лимитирующей стадии в прямом и обратном направлениях, но в этом случае выбор итогового уравнения будет определяться природой лимитирующей стадии.

Получив матрицу Г, найдём итоговое уравнение, т.е. матрицу стехиометрических коэффициентов итоговых уравнений В_Р,

и уравнения, связывающие скорости по веществу R_N и скорости по маршруту R_P

называемое условием стационарности стадий Хориути — Тёмкина. Это уравнение устанавливает связь между скоростью стадии и скоростью по маршруту и показывает, как стадии механизма перераспределяются по маршрутам. Кроме того, уравнение (19) можно использовать и для вывода уравнений для скоростей R_i и R_P (аналогично методу Боденштейна), поскольку система (19) содержит S уравнений и S неизвестных (S = N_I + P). Условие стационарности стадий (19) эквивалентно условию Боденштейна

Из (20) и (19) получаем уравнение (9), используемое для нахождения базиса маршрутов

Пример 3. Механизм гидрирования этилена (21) на поверхности твердого металлического катализатора опишем последовательностью четырех элементарных стадий:

Методы определения Км и Vmax

Константу Михаэлиса можно определить из графика Михаэлиса (рис.2.2.1), найдя графическим способом максимальную скорость и соответствующую величину концентрации субстрата, при которой скорость ферментативной реакции будет вдвое меньше Vmax. Эта величина [S] и будет Км. Таким способом можно определить только приблизительную величину константы Михаэлиса из-за трудности точного графического определения Vmax.

Более удобными являются методы, в которых осуществлена линеаризация уравнения Михаэлиса-Ментен, т. е. гиперболическая зависимость v от [S] переведена в линейную.

Для того чтобы построить такой график, необходимо определить в одинаковых условиях при различных концентрациях субстрата и [E]= const начальные скорости ферментативной реакции.

Метод Лайнуивера-Берка. Один из способов линеаризации уравнения Михаэлиса-Ментен предложили Лайнуивер и Берк (Lineweaver H., Burk D.). Это так называемый метод двойных обратных величин. Для линеаризации необходимо взять обратные величины от левой и правой частей уравнения (3), в результате чего оно преобразуется в уравнение вида,

согласно которому между величинами, обратными начальной скорости (1/v, v -1 ) и концентрации субстрата (1/[S], [S] -1 ) соблюдается линейная зависимость, если механизм реакции подчиняется изложенным выше представлениям (рис.2.2.3).

Рис. 2.2.3. График зависимости 1/v от 1/[S] (график Лайнуивера-Берка)

Экспериментальная прямая пересекает ось абсцисс в точке (-1/[S] = 1/Км), а ось ординат – в точке (1/v = 1/Vмах). Тангенс угла наклона равен Км/Vмах. Этим широко пользуются для определения параметров Км и Vмах, характеризующих связывающую и каталитическую функции ферментов.

Метод Хайнса-Вульфа. В этом случае преобразуется уравнение Лайнуивера-Берка путем умножения правой и левой частей на концентрацию субстрата.

Графическая зависимость приведена на рис.2.2.4.

Рис. 2.2.4. График зависимости [S]/v от [S] (график Хайнса-Вульфа)

Это прямая с наклоном 1/Vmax, отсекающая на осях [S]/v и [S] отрезки Км/ Vmax и – Км соответственно.

Метод Иди-Хофсти. При одном из таких графических преобразований в так называемом графике Иди-Хофсти(pиc.2.2.5) строят график зависимости v от v/[S]. В этом случае точка пересечения прямой, полученной путем наилучшей линейной аппроксимации экспериментальных точек, с осью ординат соответствует Vmax, а тангенс угла наклона равен – K_m. Данный способ линеаризации приведен на рис. 2.2.5.

Рис. 2.2.5. График зависимости v от v/[S] (график Эди-Хофсти)

Метод Эйзенталя и Корниш-Боудена. Много позднее Эйзенталь и Корниш-Боуден предложили иной метод графического представления результатов исследования кинетики ферментативных реакций – так называемый прямой линейный график. Уравнение Михаэлиса-Ментен они преобразовали в виде зависимости Vmax от Км:

Для любой пары значений [S] и v можно построить зависимость Vmax от Км. Она представляет прямую с наклоном, равным v/[S], и отрезками, отсекаемыми на осях Км и Vmax, соответственно равными -[S] v. Если провести прямые для нескольких пар значений [S] и v, то эти прямые пересекутся в одной точке, координаты которой дадут единственные значения Vmax от Км, удовлетворяющие всем парам значений [S] и v (рис.2.2.6).

Преимущества такого графика очевидно: для его построения не требуется никаких расчетов, он позволяет очень просто выявить ошибочные данные (иакие прямые будут выпадать из основной совокупности прямых).

Уравнение Михаэлиса лежит в основе всех кинетических исследований ферментативных реакций, так как оно позволяет рассчитать количественные характеристики ферментов и проводить анализ их ингибирования. Величины К_m и V_max являются важнейшими характеристиками ферментов и их можно определить, используя линеаризованные формы уравнения Михаэлиса-Ментен.

В заключении необходимо отметить, что графические методы для определения V и К_m не являются оптимальными. В настоящее время данные ферментативной кинетики обрабатывают быстрее и более объективно с помощью компьютерных программ.

Процессы, приводящие к денатурации фермента, могут иметь различную физико-химическую природу. Конформация белковой молекулы в растворе зависит от двух показателей – величины рН и температуры. Повышение температуры приводит к нарушению системы слабых связей, стабилизирующих белковую молекулу. Длительное воздействие повышенной температуры приводит к необратимым изменениям структуры фермента, сопровождающимся потерей активности (тепловая денатурация).

Каждый фермент характеризуется соответствующим зарядом, создаваемым ионогенными группами аминокислотных остатков. При очень низких или высоких значениях рН изменение степени ионизации функциональных групп может приводить к необратимым нарушениям нативной конформации молекулы фермента с разрушением структуры активного центра.

Конформационные изменения в белковой молекулу сопровождаются изменениями спектров поглощения и флуоресценции ароматических аминокислот – тирозина и триптофана в ультрафиолетовой области спектра (

290 нм), что позволяет отслеживать изменения в структуре фермента. Обратимые конформационные, вызванные изменением температуры или концентрацией протонов водорода, осуществляются в течение 10 -4 – 10 -1 с, необратимые денатурационные изменения в зависимости от условий – в течение 1-10 3 мин. Более подробный анализ кинетики денатурации ферментов рассмотрен в Теме 5 учебного пособия по самостоятельной работе.