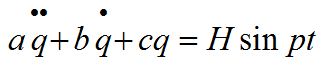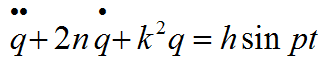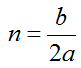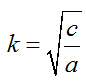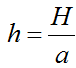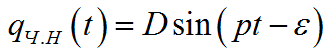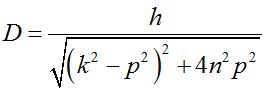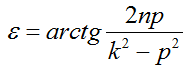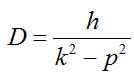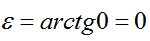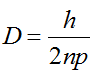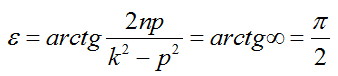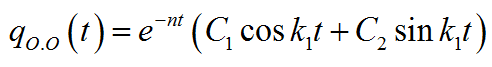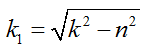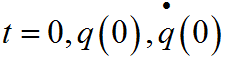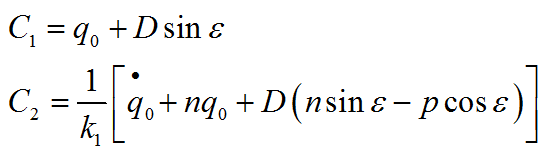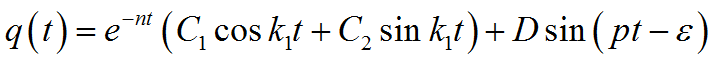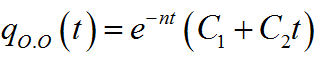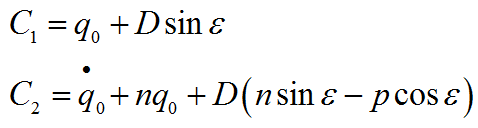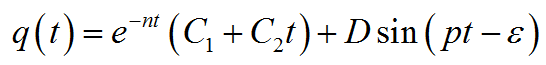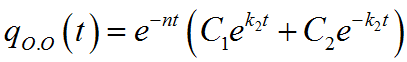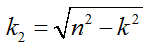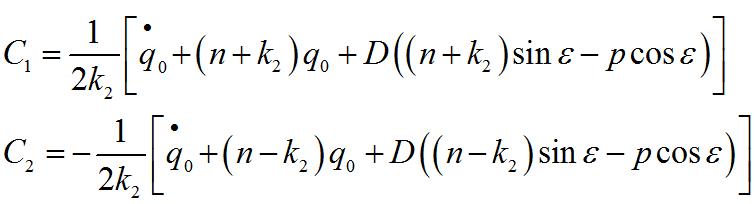Малые колебания механической системы описываются дифференциальным уравнением

Малые колебания механической системы описываются дифференциальным уравнением

Глава 21. Малые колебания механических систем.

21.1. Колебания систем с одной степенью свободы.

21.1.1. Малые колебания механической системы описываются дифферен­циальным уравнением q + (4π) 2 q = 0, где q — обобщенная координа­та, м. Начальное смещение системы q₀ = 0,02 м, начальная скорость q_o = 2 м/с. Определить амплитуду колебаний. (Ответ 0,160)

21.1.2. Определить период свободных колебаний механической системы, если дифференциальное уравнение колебаний этой системы имеет вид 56q + 825q = 0, где q — обобщенная координата. (Ответ 1,64)

21.1.3. Зубчатый венец 1 массой 40 кг может по­вернуться относительно центра 2, сжимая пружины. В положении равновесия пружины не деформированы. Определить собственную частоту малых колебаний венца. Радиус инер­ции венца 0,24 м, коэффициент жесткости одной пружины 5 • 10 5 Н/м, радиус r = 0,2 м. (Ответ 29,7)

21.1.4. Определить собственную частоту в рад/с малых колебаний однородного жесткого стержня длиной l, если его масса равна 3 кг, коэффициент жесткости пружины 400 Н/м. Стержень движется в горизонтальной плоскос­ти. (Ответ 10)

21.1.5. Квадратная однородная недеформируемая пластина массой 10 кг может вращаться в горизонтальной плоскости вокруг шарнира О. Определить собственную частоту малых коле­баний пластины, если пружины одинаковы и коэффициент жесткости каждой равен 1 кН/м. (Ответ 2,76)

21.1.6. Определить собственную частоту малых колебаний квадратной однородной недеформируемой пластины. Масса пластины 10 кг, коэффициент жесткости пружины равен 1 кН/м. (Ответ 1,95)

21.1.7. На конце торсионной рессоры 1 с коэф­фициентом угловой жесткости с_φ = 40000 Н • м/рад установлен диск 2 с моментом инер­ции I_z = 25 кг • м 2 относительно оси O_z. Диск совершает угловые колебания вокруг оси O_z. Определить угловую собственную частоту ко­лебаний. (Ответ 40)

21.1.8. Определить период свободных колебаний системы трех одинаковых зубчатых колес, если момент инерции каждого из них относительно его оси вращения равен 0,04 кг • м , а коэффициент угловой жесткости спиральной пружины 10Н • м/рад. (Ответ 0,688)

21.1.9. Определить период свободных колебаний зубчатой пары, если зубчатые колеса одинако­вы, масса каждою равна 5 кг, радиус инерции относительно оси вращения 6 см, а коэффи­циент угловой жесткости спиральной пружи­ны 1Н • м/рад. (Ответ 1,19)

21.1.10. Определить угловую частоту малых сво­бодных колебаний однородного недеформируемого диска, если его масса m = 2 кг, а коэффициенты жесткости пружин c₁ = 900 Н/м, с₂ = 700 Н/м. (Ответ 40)

21.1.11. Однородный цилиндр массой 2 кг может катиться по горизонтальной плоскости. В по­ложении статического равновесия пружина натянута силой 150Н. Определить собствен­ную частоту в рад/с малых колебаний цилинд­ра, если размер l = 0,5 м. (Ответ 10)

21.1.12. Определить момент инерции твердого тела относительно его оси вращения, если собствен­ная частота малых колебаний тела равна 4Гц, расстояние l = 2 м, коэффициент жесткости пружины с = 80 кН/м. (Ответ 507)

21.1.13. Однородный стержень длиной 0.4 м мас­сой 1,2 кг, на конце которого закреплена материальная точка массой 0,8 кг, может вра­щаться о горизонтальной плоскости. Опреде­лить коэффициент угловой жесткости спираль­ной пружины, если собственная частота колебаний этой системы равна 20Гц. (Ответ 3,0.1 • 10 3 )

21.1.14. Кинетическая энергия консервативной ме­ханической системы Т = 60q 2 , где q — обоб­щенная координата, рад. При каком значении коэффициента угловой жесткости спиральной пружины собственная угловая частота коле­баний системы будет равна 10 рад/с?
(Ответ 1,2 • 10 4 )

21.1.15. Свободные колебания жесткого стержня описываются нелинейным дифференциальным уравнением q + 300sinq — 230 sinq/(5-4cosq) 0,5 = 0, где q — обобщенная координата. Опреде­лить собственную частоту стержня в случае ма­лых колебаний.
(Ответ 1,33)

21.1.16. Консервативная механическая система со­вершает малые свободные колебания с часто­той 2Гц. Определить амплитуду колебаний ползуна 1, если в начальный момент система находилась в положении статического равнове­сия, а скорость ползуна 1 была равна v₀ = 0,2 м/с. (Ответ 0,0159)

Малые колебания механической системы описываются дифференциальным уравнением

Глава 21. Малые колебания механических систем.

21.1. Колебания систем с одной степенью свободы.

21.1.17. Колебания механической системы описываются дифференциаль­ным уравнением 9q + 4q = 2 sin 2t, где q — обобщенная координата. Совершаются ли вынужденные колебания механической системы в фазе с вынуждающей силой? (Ответ Heт)

21.1.18. Консервативная механическая система со­вершает резонансные колебания, закон изменения обобщенной координаты q во времени показан на рисунке. Во сколько раз увеличат­ся ординаты точек огибающей N, если в два раза увеличить амплитуду вынуждающей силы? (Ответ 2)

21.1.19. Колебания механической системы описываются дифферен­циальным уравнением 2q + 3q = 2 sin 5t, где q — обобщенная координата, м. Определить в мм амплитуду обобщенной координаты вынужденных колебаний. (Ответ 42,6)

21.1.20. Дифференциальное уравнение малых коле­баний тела имеет вид Iφ + сl 2 φ = lF. Опреде­лить в рад амплитуду вынужденных колеба­ний тела, если момент инерции его относитель­но оси вращения I = 6 кг • м 2 , коэффициент жесткости пружины с = 3 кН/м, размер l = 0,5 м, сила F = 10sin6 πt. (Ответ 3,62 • 10 -3 )

21.1.21. Определить декремент колебаний механической системы, если дифференциальное уравнение колебаний этой системы имеет вид 8q + 16q + 800q = 0, где q — обобщенная координата. (Ответ 1,88)

21.1.22. Определить логарифмический декремент колебаний механической системы, если дифференциальное уравнение этой системы имеет вид 15q + 30q + 900q = 0. где q — обобщенная координата. (Ответ 0,818)

21.1.23. Колебания нелинейной механической системы описываются диф­ференциальным уравнением q + 3sinq + 4q = 0, где q — обобщенная координата. Определить логарифмический декремент малых коле­баний системы. (Ответ 7,12)

21.1.24. Дифференциальное уравнение движения механической системы имеет вид 20q + 120q + 720q = 0, где q — обобщенная координата. Будет ли в этом случае движение системы апериодическим? (Ответ Нет)

21.1.25. Движение механической системы описывается дифференциальным уравнением 3q+ 6q + 2q = 0, где q — обобщенная координата. Будет ли это движение апериодическим? (Ответ Да)

21.1.26. Свободные затухающие колебания механической системы описы­ваются дифференциальным уравнением 2q + q + 8q = 0, где q — обоб­щенная координата. Во сколько раз уменьшится амплитуда колеба­ний за два периода? (Ответ 4,87)

21.1.27. Определить период свободных затухающих колебаний механичес­кой системы, если дифференциальное уравнение колебаний этой сис­темы имеет вид 12q + 48q + 432q = 0, где q — обобщенная коорди­ната. (Ответ 1,1)

21.1.28. Свободные затухающие колебания механической системы описы­ваются дифференциальным уравнением 2q + 3q + 5q = 0, где q — обобщенная координата, м. Определить обобщенную координату в момент времени t = 1 с, если в начальный момент времени обоб­щенная координата q₀ = 0, а ее производная q₀ = 1 м/с. (Ответ 0,334)

21.1.29. Колебания механической системы описываются дифференциаль­ным уравнением 5q + 10q + 125q = 12 sin 5t, где q — обобщенная координата. Определить фазовый угол установившихся вынужденных колебании. (Ответ 1,57)

21.1.30. Движение механической системы описывается дифференциаль­ным уравнением q + 4q + 9q = 10 sin 3t, где q — обобщенная коорди­ната. Во сколько раз уменьшится амплитуда установившихся вынужденных колебаний при увеличении коэффициента сопротивления в 2 раза? (Ответ 2)

21.1.31. Дифференциальное уравнение колебаний механической системы имеет вид 64q + 170q + 3000q = F, где q — обобщенная координата, м; F = 150 sin 8t — вынуждающая сила, Н. Оп­ределить амплитуду установившихся вынуж­денных колебаний. (Ответ 8,59 • 10 -2 )

21.1.32. Определить, во сколько раз уменьшится амплитуда установивших­ся вынужденных малых колебаний неконсервативной механической системы с одной степенью свободы, если амплитуда гармонической обобщенной вынуждающей силы уменьшится в 3 раза. (Ответ 3)

Теоретическая механика. Малые колебания

Дифференциальное уравнение малых вынужденных колебаний с вязким сопротивлением в общем виде выглядит так

Приводим его к каноническому виду.

— частота собственных колебаний

— амплитуда вынуждающего воздействия.

Решение данного дифференциального уравнения выглядит как сумма общего и частного решений.

Частное решение всегда выглядит одинаково. В общем виде:

— амплитуда вынужденных колебаний

— сдвиг фаз – отставание по фазе установившихся вынужденных колебаний от вынуждающей причины.

В зависимости от условий задачи возможны частные случаи.

При отсутствии вязкого сопротивления (n=0)

Если при этом собственная частота колебаний совпадает с частотой возбуждающей причины (k=p), возникает явление резонанса и амплитуда D стремится к бесконечности.

При наличии сопротивления, но равенстве n=k, резонанс невозможен.

Если по условию задачи возбуждение отсутствует (рассматриваются свободные колебания), т.е. h=0, p=0, то частное решение ДУ нулевое.

Теперь займемся общим решением.

Общее решение дифференциального уравнения зависит от соотношения k и n.

При k>n имеем случай малого сопротивления.

Для этого случая решение однородного уравнения запишем в виде:

Постоянные интегрирования определяем из начальных условий

Тогда окончательное решение дифференциального уравнения

При k=n имеем случай критического сопротивления.

Для этого случая решение однородного уравнения запишем в виде:

Постоянные интегрирования определяем из начальных условий

Тогда окончательное решение дифференциального уравнения

При k

Постоянные интегрирования определяем из начальных условий

Тогда окончательное решение дифференциального уравнения