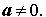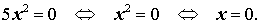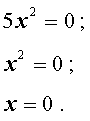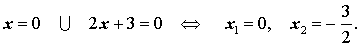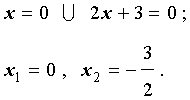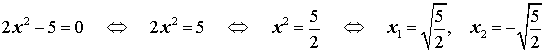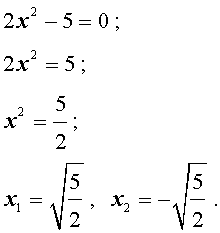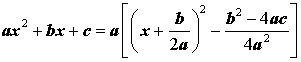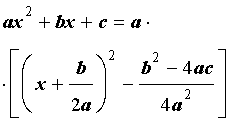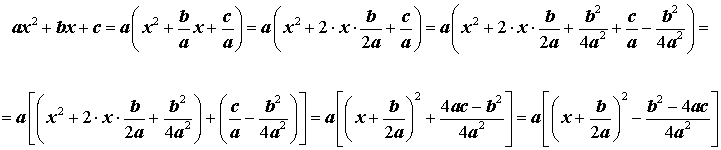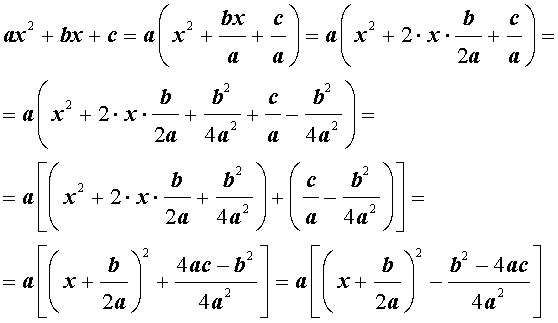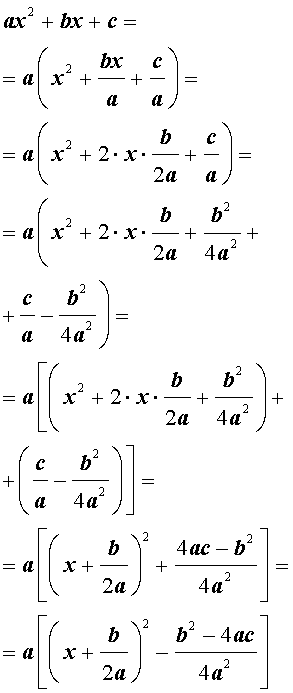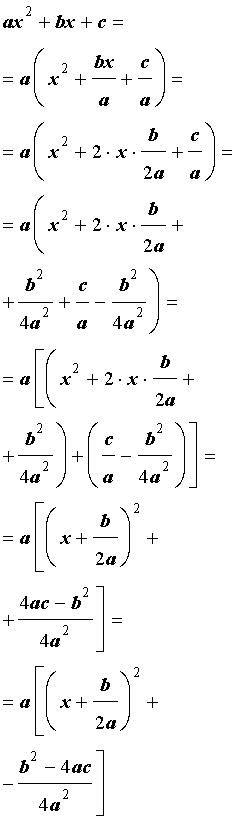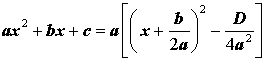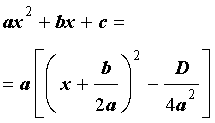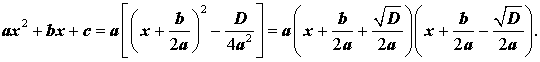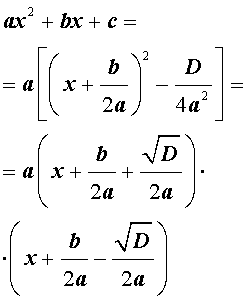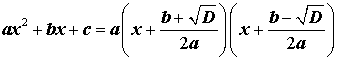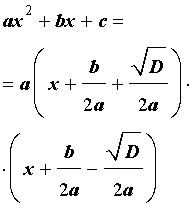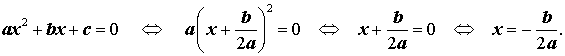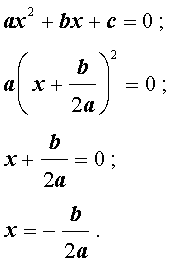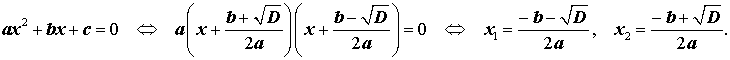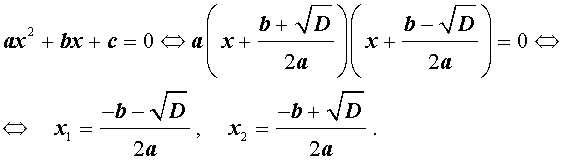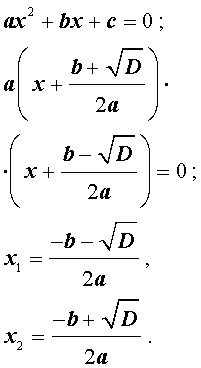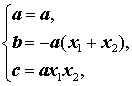О решении квадратного уравнения
Мы убедились в том, что при численном решении задач на компьютере вычислителя ожидают всякие «ловушки», которые могут привести к заметной потере точности результатов или даже к прекращению счета. Хорошей иллюстрацией к этому является анализ алгоритма решения такой простой задачи, как решение квадратного уравнения 

Из анализа этих формул видно, что здесь имеется ряд особенностей вычислительного характера, которые необходимо иметь в виду при составлении алгоритма.
Рассмотрим простейший случай а=0. Здесь уравнение становится линейным, и его единственный корень есть х = — с/b, если b≠0. При а = b= 0 и с ≠ 0 уравнение не имеет решения, а в случае а = b = с = 0 его решением будет любое число. Заметим, что в машинной арифметике редко получаются точно нулевые значения. Поэтому коэффициенты можно сравнивать не с нулем, а с некоторой малой величиной ε.
Это в свою очередь порождает ряд ситуаций, зависящих от соотношения между коэффициентами.
Далее необходимо предусмотреть разветвление алгоритма в зависимости от знака дискриминанта D: D>0 – корни действительные [см. (1.6)]; D= 0 — корни равные: х1=x2= —b/(2а); D 0 формулу для x2можно преобразовать следующим образом:
При b 0 значения корней вычисляют по формулам (1.8), (1.9). Заметим, что в приведенном на структурограмме алгоритме предусмотрены еще не все случаи возможных вычислительных затруднений, которые могут встретиться при решении квадратных уравнений.
Рис. 1.1. Структурограмма алгоритма решения квадратного уравнения
Рис. 1.2. Блок-схема алгоритма решения квадратного уравнения
Можно привести некоторые примеры, когда реализация этого алгоритма на компьютере невозможна. Будем предполагать, что вычисления проводятся с двойной точностью.
Пример 1. а = 10-200, b=-3•10-200, с = 2•10-200. При вычислении произведений b2 и 4ас получается машинный нуль, т.е. D = 0; решение пойдет по ветви равных корней: х1= х2= 1.5. Точные значения корней, как нетрудно видеть, х1 = 1, х2 = 2.
Пример 2. а=10200, b = -3•10200, с=2•10-200. Этот вариант аналогичен предыдущему случаю с той лишь разницей, что вместо получения машинного нуля произойдет переполнение и прерывание счета.
Пример 3. а = 10-200, b =10200, с=-10200. Это трудный для реализации на компьютере случай. В практических расчетах встречаются уравнения с малым коэффициентом при х2. В этом случае b2>> 4ас, но при вычислении b2 произойдет переполнение. Простейшим выходом из этого положения может быть сведение к случаю а = 0 с обязательной проверкой других коэффициентов.
Таким образом, анализ даже такой задачи, как решение квадратного уравнения, показывает, что использование численного алгоритма может быть сопряжено с некоторыми трудностями.
Логико-математический анализ содержания темы «Квадратное уравнение»
Разделы: Математика
Тема «Квадратные уравнения» в курсе алгебры 8 класса по программе Ю.Н. Макарычева, Н.Г. Миндюк разбита на 11 часов. На первых уроках даётся общий вид квадратного уравнения, вводится неполное квадратное уравнение (п.21 по учебнику Ю.Н. Макарычева, 2ч.), понятие приведенного квадратного уравнения. Далее приводится алгоритм решения уравнений по формулам через дискриминант (п.22, 3ч.).
В этой теме отводится параграф и на решение задач с помощью квадратного уравнения, начиная с простейших до более сложного уровня (п.23, 2ч.), что позволяет ученику выбирать и осваивать свой уровень знакомства с темой, её усвоением.
Говоря о решении квадратного уравнения, можно показать несколько способов их решения, одним из таких является нахождение корней по теореме Виета. Этот материал знакомит учащихся и с новыми формулами, доступными для запоминания и понимания. Дает учащимся возможность подготовить сообщение по теореме; о биографии французского математика Ф.Виет.
Тема «Квадратные уравнения предусматривает одну самостоятельную работу и заканчивается выполнением контрольной работы №5. После чего ребятам даётся понятие дробно-рационального уравнения, уравнения, сводящегося к квадратному.
Таким образом, в ходе работы над темой в школьном курсе алгебры 8 класса учащиеся
– определение квадратного уравнения, неполного, приведенного;
– формулы для нахождения его корней, алгоритм их поиска через дискриминант и по теореме Виета;
– теорему обратную теореме Виета.
– определять по виду квадратное уравнение, неполное, приведенное;
– решать неполное квадратное уравнение;
– определять количество корней в уравнении;
– решать квадратное уравнение по формулам;
– применять т. Виета при решении;
– решать задачи с помощью квадратных уравнений.
Логико-математический анализ задач по теме включает:
- Выявление видов задач (и возможностей составления предписаний определённого типа для их решения).
- Выявление методов решения задач: на доказательство, на вычисление, на построение и их количества.
- Выявление обоснований решения задач: базиса решения.
- Выявление аналогичных задач.
- Выявление опорных задач.
Цели обучения теме «Квадратные уравнения»
В ходе изучения данной темы рассматривается целый ряд целей. Согласно Программе развития универсальных учебных действий (УУД), о формировании которых так много говорится в ФГОС ООО, к формированию которых мы и должны стремиться на каждом из уроков, речь идет о четырёх видах:
1) познавательные; 2) регулятивные; 3) коммуникативные; 4) личностные.
Рассмотрим на примере темы «Квадратные уравнение» формирование каждого из них.
2.1. Развитие познавательных УУД.
В ходе изучения темы учащийся должен научиться сравнивать квадратные уравнения по признакам и составлять схему определения понятия данного вида уравнения; сравнивать решение однотипных. Должен выполнять анализ и выявлять необходимые преобразования. Составляет приёмы решения уравнения, решает уравнения по теореме Виета. Эти цели чаще ставятся на первых уроках, где знания учащихся только формируются.
2.2. Развитие регулятивных УУД.
Развивая регулятивные УУД, учащиеся самостоятельно выбирают уровень освоения темы, выбирают задачи. Осуществляют самопроверку, составляют план своих действий при изучении темы и оценивают свою работу, свои действия при изучении темы.
2.3. Развитие коммуникативных УУД.
На мой взгляд, одной из самых важных этапов урока – это формирование коммуникативных учебных действий у учащихся. В век компьютерных технологий, где дети проводят большое количество времени в социальных сетях, где заводят виртуальных друзей, в результате чего живое общение сводится к нулю. На уроках важно научить высказывать свои мысли; давать полные формулировки понятий. Уметь ставить вопросы, проводить дискуссии по теме. Ученик на этом этапе должен научиться работать в группе, оказывая помощь. При изучении темы «Квадратные уравнения» ученику даётся возможность выступить с сообщением. Очень полезно при формировании коммуникативных УД научить ребёнка разбирать, анализировать ошибки в ходе решения.
2.4. Развитие личностных УУД.
Личностные учебные действия включают самопознание и самоопределение. Способствует профессиональному, жизненному самоопределению и построению жизненных планов. На уроках по данной теме ученик должен определиться с результатами своей деятельности при решении уравнений, своих мотивов. Учитель должен показать значимость этой темы, решение задач с помощью квадратных уравнений.
Карта изучения темы и её использование
В ходе работы над темой в рамках ФГОС ООО был разработан полезный материал как для учителя так и для ученика – карта изучения темы «Квадратные уравнения» в курсе алгебры 8 класса (Приложение 1). Эта карта вывешивается на стенде для знакомства учащихся с этапами ознакомления темы, где указаны уровни обучения теме, с которыми ребёнок вправе сам определиться, спланировать свои действия при обучении.
Если говорить подробнее, то карта изучения темы включает в себя 8 блоков:
1. Логическая структура и цели изучения темы;
2. Блок актуализации знаний учащихся;
3. Основные понятия, методы, изучаемые в теме;
4. Примеры заданий контрольной работы;
5. Средства обучения теме;
6. Задания для внеурочной самостоятельной работы;
7. Темы индивидуальных заданий;
8. Перечень УУД для освоения темы.
Карта составляется учителем перед изучением темы, планируя каждый урок, особенно деятельность учащегося во время формирования знаний и дальнейшего изучения темы. (Приложение 2).
Квадратные уравнения
 Решение неполных квадратных уравнений Решение неполных квадратных уравнений |
 Выделение полного квадрата Выделение полного квадрата |
 Дискриминант Дискриминант |
 Разложение квадратного трехчлена на множители Разложение квадратного трехчлена на множители |
 Формула для корней квадратного уравнения Формула для корней квадратного уравнения |
 Прямая и обратная теоремы Виета Прямая и обратная теоремы Виета |
Квадратным трёхчленом относительно переменной x называют многочлен
| ax 2 + bx + c , | (1) |
где a, b и c – произвольные вещественные числа, причем
Квадратным уравнением относительно переменной x называют уравнение
| ax 2 + bx + c = 0, | (2) |
где a, b и c – произвольные вещественные числа, причем
Полным квадратным уравнением относительно переменной x называют уравнение
где a, b и c – произвольные вещественные числа, отличные от нуля.
Неполными квадратными уравнениями называют квадратные уравнения следующих типов:
 | 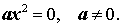 |
 | 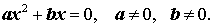 |
 | 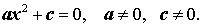 |
Решение неполных квадратных уравнений
Покажем, как решаются неполные квадратные уравнения на примерах.
Пример 1 . Решить уравнение
Пример 2 . Решить уравнение
| 2x 2 + 3x= 0 . | (3) |
Решение . Вынося в левой части уравнения (3) переменную x за скобки, перепишем уравнение в виде
| x (2x+ 3) = 0 . | (4) |
Поскольку произведение двух сомножителей равно нулю тогда и только тогда, когда, или первый сомножитель равен нулю, или второй сомножитель равен нулю, то из уравнения (4) получаем:
Ответ : 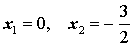
Пример 3 . Решить уравнение
Ответ : 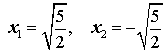
Пример 4 . Решить уравнение
| 3x 2 + 11 = 0 . | (5) |
Решение . Поскольку левая часть уравнения (5) положительна при всех значениях переменной x , а правая часть равна 0, то уравнение решений не имеет.
Ответ : 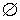
Выделение полного квадрата
Выделением полного квадрата называют представление квадратного трёхчлена (1) в виде:
Для того, чтобы получить формулу (6), совершим следующие преобразования:
Формула (6) получена.
Дискриминант
Дискриминантом квадратного трёхчлена (1) называют число, которое обозначается буквой D и вычисляется по формуле:
| D = b 2 – 4ac. | (7) |
Дискриминант квадратного трёхчлена играет важную роль, и от того, какой знак он имеет, зависят различные свойства квадратного трёхчлена.
Используя дискриминант, формулу (6) можно переписать в виде
Разложение квадратного трёхчлена на множители
Утверждение . В случае, когда 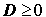
Доказательство . В случае, когда D = 0 , формула (8) и является разложением квадратного трехчлена на линейные множители:
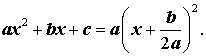 | (9) |
В случае, когда D > 0 , выражение, стоящее в квадратных скобках в формуле (8), можно разложить на множители, воспользовавшись формулой сокращенного умножения «Разность квадратов»:
Таким образом, в случае, когда D > 0 , разложение квадратного трехчлена (1) на линейные множители имеет вид
В случае, когда D , выражение, стоящее в квадратных скобках в формуле (8), является суммой квадратов и квадратный трёхчлен на множители не раскладывается.
Замечание . В случае, когда D , квадратный трехчлен всё-таки можно разложить на линейные множители, но только в области комплексных чисел, однако этот материал выходит за рамки школьного курса.
Формула для корней квадратного уравнения
Из формул (9) и (10) вытекает формула для корней квадратного уравнения .
Действительно, в случае, когда D = 0 , из формулы (9) получаем:
Следовательно, в случае, когда D = 0 , уравнение (1) обладает единственным корнем, который вычисляется по формуле
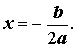 | (11) |
В случае, когда D > 0 , из формулы (10) получаем:
Таким образом, в случае, когда D > 0 , уравнение (1) имеет два различных корня , которые вычисляются по формулам
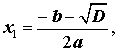 | (12) |
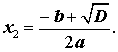 | (13) |
Замечание 1 . Формулы (12) и (13) часто объединяют в одну формулу и записывают так:
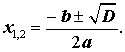 | (14) |
Замечание 2 . В случае, когда D = 0 , обе формулы (12) и (13) превращаются в формулу (11). Поэтому часто говорят, что в случае, когда D = 0 , квадратное уравнение (1) имеет два совпавших корня , вычисляемых по формуле (11), а саму формулу (11) переписывают в виде:
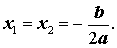 | (15) |
Замечание 3 . В соответствии с материалом, изложенным в разделе «Кратные корни многочленов», корень (11) является корнем уравнения (1) кратности 2.
В случае, когда D = 0 , разложение квадратного трехчлена на линейные множители (9) можно переписать по-другому, воспользовавшись формулой (15):
| ax 2 + bx + c = = a (x – x1) 2 . | (16) |
В случае, когда D > 0 , разложение квадратного трехчлена на линейные множители (10) с помощью формул (12) и (13) переписывается так:
| ax 2 + bx + c = = a (x – x1) (x – x2) . | (17) |
Замечание 4 . В случае, когда D = 0 , корни x1 и x2 совпадают, и формула (17) принимает вид (16).
Прямая и обратная теоремы Виета
Раскрывая скобки и приводя подобные члены в правой части формулы (17), получаем равенство
Отсюда, поскольку формула (17) является тождеством, вытекает, что коэффициенты многочлена
равны соответствующим коэффициентам многочлена
Таким образом, справедливы равенства
следствием которых являются формулы
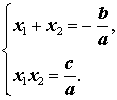 | (18) |
Формулы (18) и составляют содержание теоремы Виета (прямой теоремы Виета) .
Словами прямая теорема Виета формулируется так: — «Если числа x1 и x2 являются корнями квадратного уравнения (1), то они удовлетворяют равенствам (18)».
Обратная теорема Виета формулируется так: — «Если числа x1 и x2 являются решениями системы уравнений (18), то они являются корнями квадратного уравнения (1)».
Для желающих ознакомиться с примерами решений различных задач по теме «Квадратные уравнения» мы рекомендуем наше учебное пособие «Квадратный трехчлен».
Графики парабол и решение с их помощью квадратных неравенств представлены в разделе «Парабола на координатной плоскости. Решение квадратных неравенств» нашего справочника.
http://urok.1sept.ru/articles/652599
http://www.resolventa.ru/spr/algebra/kv.htm