Математическая модель напряженного состояния это система уравнений

Математическая модель напряженно-деформированного состояния тела

Введение

1) наука, изучающая законы и методы накопления, передачи и обработки информации с помощью ЭВМ;

2) родовое понятие, охватывающее все виды человеческой деятельности, связанные с применением ЭВМ.

Предметом информатики является изучение закономерностей взаимодействия человека с ЭВМ во всех видах его деятельности.

В основе методологии в информатике лежит принцип исследования любого явления (физического, социального, биологического и т.д.) как процесса обработки информации, на основании единых законов обработки информации.

Как фундаментальная наука информатика связана с философией – через учение об информации как общенаучной категории и теорию познания, с математикой через понятия математического моделирования, логику и теорию алгоритмов; с лингвистикой – через учение о формальном языке и знаковых системах, а также со специальными науками: теория информации, кибернетика, системотехника и др.

С предметом информатики тесно связаны определенные виды человеческой деятельности, к которым относятся: математическое моделирование (фиксация результатов познавательного процесса в виде математической модели); алгоритмизация (реализация причинно-следственных связей и других закономерностей в виде направленного процесса обработки информации по формальным правилам); программирование (реализация алгоритма на ЭВМ); вычислительный эксперимент (получение нового знания об изучаемом явлении с помощью вычислений на ЭВМ); решение конкретных задач, относящихся к кругу объектов и явлений, описанных исходной моделью.

Известно, что при проектировании любой конструкции неизбежен этап расчета на прочность (способность конструкции выдерживать определенную нагрузку не разрушаясь) и жесткость (способность конструкции противостоять внешним нагрузкам при ограниченных деформациях), устойчивость (способность элементов конструкции сохранять определенную начальную форму упругого равновесия).

В этом направлении, задача строительной информатики (как вида информатики вообще) состоит в разработке и применении компьютерных технологий для проведения инженерного анализа конструкции сооружений (или для решения задач строительного профиля).

Необходимость решения широкого спектра прикладных задач, привела к возникновению большого количества программного обеспечения, относительно доступного массовому пользователю.

Современные инженеры-расчетчики, для решения задач расчета строительных конструкций, широко используют компьютерные технологии и специализированные пакеты прикладных программ, такие как, SCAD, ANSYS, Lira, NASTRAN, COSMOS, ADINA, MIDAS и др. Данные программы позволяют значительно расширить круг решаемых задач, в плане усложнения используемых расчетных схем, детализирования расчетных моделей, увеличения размерности, и т.д. Математической основой, на которой построен вычислительный аппарат этих программных продуктов, является метод конечных элементов. В сущности, не имеет значения, какой пакет использовать для расчета конструкций методом конечных элементов, принцип работы с ним напоминает работу с «черным ящиком» с помощью которого, задавая только входные данные и не вникая в сущность алгоритмов, на выходе получают результат. Так что выбор готовой программы это выбор в пользу соотношения «цена\качество», где цена – это время освоения пакета, а качество – знания, приобретаемые в процессе обучения. Неплохим способом может служить написание собственного пакета, реализующего метод конечных элементов, если имеется достаточное количество базовых знаний.

Розин Л.А. « От расчетчика пользователя программными комплексами, интересующегося напряженно-деформированным состоянием, не требуется детального знания всех математических, вычислительных и компьютерных проблем. Однако ему необходимо иметь представление о том, как математически формулируются задачи и что представляют собой численные методы их решения. Без этого трудно рационально выбрать расчетную схему и правильно оценить достоверность окончательных результатов».

Главной задачей курса является разобраться в структуре общего подхода к решению задач расчета строительных конструкций.

Основные вопросы курса:

1. Математическая постановка расчетных инженерных задач.

2. Обсуждение алгоритмов и численных методов решения задач расчета конструкций.

3. Выбор программного обеспечения для реализации расчетов.

Требования к уровню подготовки слушателей:

1. Высшая математика;

2. Строительная механика;

3. Опыт выполнения расчетов с использованием ЭВМ.

(С точки зрения логики всякое понятие имеет содержание (отличительные признаки понятия) и объем (множество обобщенных в нем предметов). Например «товар» – любая вещь, участвующая в свободном обмене на другие вещи. Объем понятия «товар» – множество всех изделий, предлагаемых рынку как сейчас, так и в прошлом и в будущем. Родовым называется понятие, объем которого шире и полностью включает в себя объем другого понятия. Видовым называется понятие, объем которого составляет лишь часть объема другого понятия).

Математическая модель напряженно-деформированного состояния тела

Решение задачи расчета конструкции, начинается с разработки математической модели деформирования этой конструкции, основанной на законах и теоремах общей механики и положениях теории упругости.

Под математической моделью понимают совокупность математических объектов и соотношений, которые приближенно отображают реальные объекты и отношения некоторой предметной области.

При построении математической модели принимаются некоторые гипотетические предположения, которые не противоречат физическим законам, законам природы, практике (эксперименту) и здравому смыслу.

Рассмотрим основные гипотезы, используемые в теории упругости.

1. Гипотеза сплошной среды. Модель сплошной среды

а) предполагает, что масса (вещество) не сосредоточена в молекулах и атомах, а непрерывно распределена (размазана) по всему объёму, занятому физическим телом;

б) учитывает деформацию тела под действием приложенных сил;

в) позволяет использовать аппарат непрерывных функций, дифференциального и интегрального исчисления.

2. Гипотеза о физической однородности. Согласно ей все физические характеристики тела (модули упругости, коэффициенты Пуассона, плотности и т.д.) не зависят от координат точек тела.

3. Гипотеза, согласно которой материал тела является идеально упругим (форма и размеры полностью восстанавливаются после устранения причин, вызвавших деформации), а между деформациями и напряжениями существует линейная зависимость (закон Гука).

Далее, при построении математической модели необходимо определить исходные данные (входные параметры), переменные задачи и искомые величины (параметры результаты). В задачах деформации заданными можно считать геометрию тела, свойства материала, внешнюю нагрузку, способ закрепления. 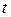Поскольку, напряженно-деформированное состояние определяется в каждой точке тела, то переменными задачи считают координаты точки , и возможно, время (в задачах динамики).

Напряженно-деформируемое состояние в точке тела полностью характеризуется векторными функциями: перемещением, деформацией и напряжением. Гипотеза сплошной среды позволяет рассматривать эти функции как непрерывные функции координат и использовать анализ бесконечно малых. Между этим функциями существует определённая связь, в виде математических соотношений, которые в линейной теории упругости строятся на нескольких простых естественных предположениях:

1. Перемещения точек тела предполагаются малыми по сравнению с его характерным размером и углы поворота прямолинейных отрезков в точках тела малы по сравнению с единицей. Отсюда следует, малость деформаций, т.е. малость относительных удлинений и сдвигов по сравнению с единицей.

2. Уравнения, связывающие напряжения и деформации, имеют вид линейных алгебраических соотношений.

3. В процессе деформирования не происходит изменений характера контакта между отдельными частями внутри тела, а также на границе при взаимодействии его с другими телами.

Рассмотрим основные характеристики напряженно-деформированного тела и связывающие их зависимости.

Пусть на трехмерное тело, закрепленное определенным образом (невозможно смещение тела, как единого целого), действуют нагрузки. Отнесем это тело к системе координат . Под действием приложенных нагрузок тело деформируется (меняет свою форму и внутренние свойства).

Изменение формы тела связано с перемещениями его точек. Это значит, что каждая точка , имеющая координаты до деформации, в результате деформации перемещается в новое положение с координатами . Приращение координат точки называются перемещениями этой точки вдоль осей . Вектор называется вектором перемещений. Компоненты вектора перемещений зависят от координат точки , , и являются непрерывными функциями.

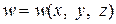
Рис. 1. Перемещение точек тела

Бесконечно близкая к точке точка (конец отрезка) получит перемещения с координатами и переместиться в точку .

Рис. 2. Деформация прямолинейного отрезка

Под деформацией сплошного тела понимается такое изменение положения его точек, при котором изменяются взаимные расстояния между ними.

Отрезок соединяющий точку с любой точкой , находящейся в её бесконечно малой окрестности после деформации переместится в отрезок длиной .

Проекции отрезка будут определяться соотношениями:

, (1)

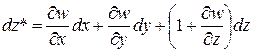
Составляя разность квадратов расстояний, в которой пренебрегаем квадратами и произведениями производных от перемещений, получим

. (2)

Выясним смысл компонент, входящих в правую часть.

Рассмотрим элементарный отрезок параллельный оси и определим относительное удлинение отрезка :

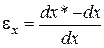
Тогда ,

Сравнивая с формулой (2), получаем .

Аналогичным образом, 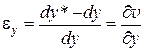и равны относительным удлинениям бесконечно малых отрезков , которые до деформации были параллельны осям координат .

Рассмотрим два бесконечно малых отрезка и , параллельных до деформации осям и , которые переместились в результате деформации в отрезки и .

Проекции отрезка после деформации равны , (в силу (1)). Угол, на который изменился прямой угол между отрезками и , обозначим .

В силу малости деформаций можно приближенно считать, что угол поворота ( ) отрезка равен .

Рис. 3 Изменение угловых величин в результате деформирования

Аналогично, угол поворота отрезка равен . Следовательно, прямой угол между отрезками и уменьшается при деформации на величину . Аналогично величины , имеют смысл изменений первоначально прямых углов между линейными элементами и в соответствующих плоскостях.

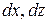
В итоге, формулу (2) можно переписать в виде

. (2’)

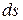
Отсюда следует, что длина (квадрат длины) отрезка в который перешел отрезок полностью определиться шестью величинами, , связанными с перемещения соотношениями

(3)

которые называются геометрическими соотношениями (в линейном теории упругости это формулы Коши).

Величины 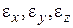называются деформациям удлинения (продольными или линейными деформациями), величины и называются деформациям сдвига.

Шесть компонент деформаций , достаточных для того, чтобы полностью характеризовать деформированное состояние тела в окрестности данной точки, формально, можно считать компонентами вектора деформаций

Замечание 1. В задачах, в которых перемещения тела нельзя считать малыми, используются нелинейные геометрические уравнения. В таком случае говорят о геометрически-нелинейной теории упругости.

Рассмотрим силовые характеристики напряженно-деформированного состояния. Для того чтобы описать взаимодействие конструкции с окружающей средой вводиться понятие нагрузки, представляемой в расчетной схеме в виде системы сил. Взаимодействие рассматриваемого объекта с телами, расположенными за пределами условно очерченной границы, характеризуется силами, которые относятся к категории внешних сил. Различают поверхностные и объемные внешние силы. Поверхностные силы могут быть приложены к малым участкам поверхности (это сосредоточенные силы) или к конечным участкам поверхности (это распределённые силы). Они характеризуют взаимодействие объекта с другими телами или внешней средой (например, с потоком воздуха, жидкости). Объемные силы распределены по объёму тела (например, силы тяжести, инерции и т.п.). К числу внешних относят не только заданные силы, но также и реакция связей.

Взаимодействие между частями рассматриваемого объекта внутри очерченной области характеризуют внутренние силы.

Чтобы характеризовать закон распределения внутренних сил по сечению необходимо ввести для них числовую меру. За такую меру принимается напряжение. Напряжение – силовой фактор, представляющий собой интенсивность действия внутренних сил, т.е. усилие, приходящееся на единицу площади, выделенную в какой-либо точке рассматриваемого сечения.

Рассмотрим сечение некоторого тела. Воздействие одной части тела на другую состоит в том, что на поверхности действуют силы, которые для тела в целом являются внутренними силами. Под действием этих сил и приложенных внешних сил каждая из частей находится в равновесии. Если рассматривать равновесие части (2), то действие на неё части (1) надо заменить силами, распределенными по поверхности . Выделим на поверхности площадку с нормалью , проведенную в некоторой средней точке .

Рис. 4 Вектор напряжения в точке тела

Обозначим через 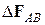силу, действующую на элементарную площадку . Отношение называется средней поверхностной силой или средним напряжением, приходящимся на единицу площади.

Этот вектор обозначается

Стягивая в точку , получим

– полное напряжение в точке (плотность поверхностной силы).

Если провести через точку другую поверхность , можно получить другой вектор напряжений . Таким образом, в точке существует бесконечно много векторов напряжений , соответствующих бесконечному числу площадок . Однако между ними существует универсальная связь.

Выделим в теле элементарную (в отношении напряжений) пирамиду с вершиной в точке , три грани которой перпендикулярны выбранным осям координат . Обозначим через – единичный вектор нормали к наклонной грани . Пусть – напряжение, действующее на грани ; , , – напряжения, действующие на гранях, перпендикулярных к осям координат.

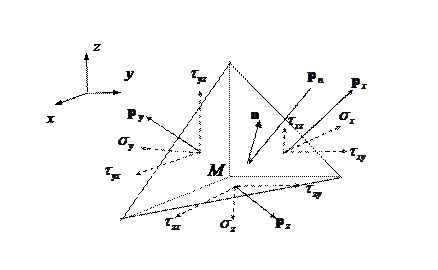Рис. 5 Напряжение на наклонной площадке

Из теории упругости известна формула, связывающая напряжение, действующее на произвольную площадку с нормалью и площадки перпендикулярные осям координат

Формула называется формулой Коши для напряжения, действующего на площадку с нормалью .

Таким образом, зная три вектора напряжения, действующие на взаимно ортогональные площадки, можно найти напряжение на произвольно ориентированной площадке.

Обозначим проекции векторов, стоящих в правой части формулы, на оси прямоугольной декартовой системы координат:

, , .

Компоненты напряжений: называются нормальными напряжениями; компоненты напряжений: называются касательными напряжениями. В большинстве случаев справедлив закон парности касательных напряжений:

Таким образом, шесть величин однозначно характеризуют напряженное состояние в точке тела и можно рассматривать вектор напряжений

Среднее арифметическое трех нормальных компонентов напряжений называется средним напряжением в точке

Для оценки прочности в каждой точке твердого тела вводятся некоторые дополнительные характеристики напряженно- деформированного состояния:

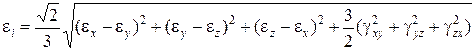
Компоненты напряжений связаны с компонентами деформаций соотношениями, которые называют физическими соотношениями.

Физические отношения, связывающие напряжения и деформации, зависят от физических свойств конструкции (материала конструкции), которые проявляются в зависимости от уровня нагружения и длительности воздействия на конструкцию нагрузки (упругие, пластические, свойства ползучести и т.д.).

Тела, для которых справедлив закон Гука , называются линейно-упругими изотропными телами, где – модуль упругости материала.

Рис. 6 Диаграмма растяжения

В общем случае напряженного состояния справедлив обобщенный закон Гука

(4)

– коэффициент Пуассона, – модуль упругости второго рода или модуль сдвига.

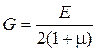
Эти соотношения могут быть разрешены относительно компонент напряжений, и получим закон Гука в обратной форме:

(4’)

где , .

Замечание 2. Большое количество практических задач расчета строительных конструкций можно решить в пределах действия закона Гука. Если для материала не применим закон Гука, то опытным путем строят диаграмму растяжения образца « 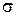– », после чего записывается функциональная зависимость . Эти задачи называются физически нелинейными, они также рассматриваются в курсе нелинейной теории упругости.

Помимо физических соотношений компоненты напряжений должны удовлетворять уравнениям равновесия

(5)

где – проекции вектора объемной силы в точке тела.

Таким образом, задача определения напряженно-деформированного состояния тела сводится к разрешающей системе уравнений, состоящей из трех групп соотношений: геометрические, физические, уравнения равновесия. Эти 15 уравнений связывают 15 неизвестных. Для получения единственного решения система уравнений (3), (4), (5) должна быть дополнена краевыми условиями

(6)

, (7)

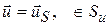
Здесь – вектор заданных перемещений на границе тела , – вектор заданных поверхностных сил на границе тела , – направляющие косинусы внешней нормали к границе тела .

Если из геометрических уравнений (3) с помощью физических уравнений (4) исключить деформации, то напряжения можно выразить непосредственно через перемещения. Затем после подстановки напряжений в уравнения равновесия (5) и статические краевые условия (7), получим постановку задачи теории упругости в перемещениях, которая известна как краевая задача для перемещений.

Однако возможна и другая математическая постановка задачи для перемещений в упругом теле, основанная на одном из важнейших принципов механики – вариационном принципе Лагранжа, который формулируется так: среди всех возможных перемещений, удовлетворяющих кинематическим граничным условиям, действительными являются перемещения, приводящие к минимуму функционала полной потенциальной энергии.

Полная потенциальная энергия тела, объема

, (8)

(9)

– потенциальная энергия деформации;

– работа внешних сил:

– работа внешних объемных сил;

– работа поверхностных сил.

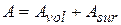
Рассматривая потенциальную энергию деформации как функционал шести компонентов деформации, математическая модель задачи теории упругости для перемещений, будет иметь вид вариационной задачи:

. (10)

Вариационная и краевая задачи связаны между собой. Характер этой связи будет рассмотрен в дальнейшем.

О некоторых математических моделях напряженного состояния пластической среды при осесимметричной деформации Текст научной статьи по специальности « Физика»

Аннотация научной статьи по физике, автор научной работы — В. Л. Дильман

В работе при некоторых допущениях получены приближенные математические модели напряженного состояния поперечной пластически деформируемой мягкой прослойки цилиндрического образца, в форме краевых задач для систем уравнений гиперболического типа, в том числе с постоянными на характеристиках римановыми инвариантами, что позволяет перенести метод характеристик на некоторые случаи осесимметричной деформации неоднородных сред.

Текст научной работы на тему «О некоторых математических моделях напряженного состояния пластической среды при осесимметричной деформации»

О НЕКОТОРЫХ МАТЕМАТИЧЕСКИХ МОДЕЛЯХ НАПРЯЖЕННОГО СОСТОЯНИЯ ПЛАСТИЧЕСКОЙ СРЕДЫ ПРИ ОСЕСИММЕТРИЧНОЙ ДЕФОРМАЦИИ

1. Введение. Задачи, приводящие к осесимметричному напряженно-деформированному состоянию (НДС), возникают при экспериментальном исследовании свойств материалов (растяжение и сжатие стержневых цилиндрических образцов, деформирование под действием осевой силы и внутреннего давления трубчатых образцов), при изучении НДС поперечных прослоек (мягких и твердых) в таких образцах и при исследовании шейки. Известные точные решения [1,2] относятся к гипотетическим состояниям и практически бесполезны в реально возникающих задачах. Попытки получения приближенных решений 5 основаны на использовании упрощающих условий и допущений (нередко противоречащих друг другу [5]) инженерного характера и не содержат анализа допускаемых ошибок. Существенной трудностью исследования осесимметрич-ного НДС является негиперболичность соответствующей системы уравнений [1]. Однако и в ряде частных случаев, когда система уравнений гиперболична, инварианты Римана не постоянны на характеристиках, а их дифференциалы вдоль последних зависят от искомых функций, что не позволяет получить метод характеристик, аналогичный методу решения плоских задач теории пластичности [6]. Один из путей преодоления указанной трудности — замена системы уравнений НДС пластической среды на приближенную на основе некоторых физических гипотез, соответствующих изучаемой ситуации, и математического анализа априорных свойств решений.

В работе рассматривается НДС мягкой поперечной прослойки в сплошном цилиндрическом образце под осевой нагрузкой. Цель работы — получение и исследование упрощенных систем уравнений пластического равновесия материала прослойки и материала твердой части образца вблизи прослойки. На основе этого исследования можно судить о развитии напряженного состояния в прослойке и прилежащих к ней участках с ростом нагрузки вплоть до потери несущей способности образца.

В работе под прослойкой понимается участок цилиндрического образца, расположенный между двумя ортогональными оси образца плоскостями. Предполагается, что материал прослойки (П) и основной металл (ОМ) образца идеально упругопластичный с идентичными упругими свойствами, но разными пределами текучести: к? и ком соответственно, К1 )2 + 6г2 = 6 ; (3)

8У2 _ ¿Н>г = 0, тп(1;г) = 0, г,2(0;2г) = 0, тГ2(г;0) = 0 (6)

(считаем внешнее давление отсутствующим), можно еще найти (в принципе, как функцию достигнутой внешней нагрузки) наибольшее на контактной поверхности г- х значение а (О

причем собственные числа матрицы этой системы действительны и различны.

3. Система (14), (15) не является однородной относительно частных производных, поэтому инварианты Римана [8] не постоянны вдоль характеристик. Это обстоятельство требует дальнейшего упрощения системы уравнений пластического равновесия (14), (15).

3. Моделирование однородной системы уравнений пластического равновесия. Введем обозначение 2(г) =

. Из (12) и (11) следует

Тгг =/Д/Г^, 1 = 12(2). (16)

Если в разложении

= + И Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

-л/Зг + у8 — 5г2 4л/1-т2

Уравнения характеристик имеют вид

со знаком плюс в (24) — £ -характеристики (пусть это будет Хх), со знаком минус — г] -характеристики. Угол у наклона -характеристики к оси Ог зависит от значения т в точке вычисления: tgу

Собственные векторы, соответствующие собственным значениям (24), имеют вид /, =(1;Л>), / = 1;2. В характеристической форме [8] система (23) записывается в виде

а в инвариантной форме [8]

где ¡лг = //,(г) — произвольная первообразная функции Яг (/’ = 1;2) . На характеристиках уравнения (26) запишутся в виде

где дифференцирование ведется в направлении характеристик. Следовательно, инвариантны Ри-мана 1г (27) постоянны на характеристиках:

1г-аг+ /лг= const, / = 1;2 . (28)

Можно считать, в силу (24),

где через Е(ср\т) обозначен эллиптический интеграл второго рода [9]. Здесь ^ = агсзтг, т = 0,5^(а + 4)/(а + \) .

Пусть СА и СА1 — £ — и г/ -характеристики, выходящие на свободную поверхность ААХ в угловых точках сечения прослойки А и Ах; С — точка их пересечения. По условию (6), аг = 0 и г Т2 = 0 на поверхности АА1, поэтому для любой точки В внутри или на границе треугольника АСАХ, в силу (28),

аг(П) + = 0, / = 1;2. Из (29) легко вывести, что г(П) — 0 и аг (В) = 0; тогда по (11), = л/з . Таким образом,

в треугольнике АСАХ реализуется равномерное напряженное состояние, причем в этом треугольнике, в силу (24),

\1а/(а +1) 5 а уравнения характеристик (25) имеют вид

(плюс у £-характеристик). В частности, расстояние от точки С — вершины треугольника равномерного напряженного состояния, — до свободной поверхности ААХ равно + а х > а угол наклона £ -характеристики в треугольнике АСА1

4. Случай малых касательных напряжений. При значениях а порядка нескольких десятых можно найти несложные приближенные аналитические выражения для функций и, как следствие, для напряжений и уравнений характеристик. Используя разложение в степенной ряд степени бинома [9], получаем по формуле (29)

причем относительная ошибка в этом приближенном равенстве оценивается величиной 0,125а(а + 1)_1г2 и при ±4 — т—г =сопз!.

Отсюда следует, что во всех точках 7] -характеристики, выходящей на свободную поверхность,

I а л/з 2 I а л/3(2а + 1) 2 , п:

\а +1 4(а +1) * +1 4(а + 1)

Аналогично выводятся приближенные уравнения характеристик (плюс соответствует £ -характеристикам)

Надоели баннеры? Вы всегда можете отключить рекламу.

Математическое моделирование напряженного состояния неоднородных цилиндрических стержней тема диссертации и автореферата по ВАК РФ 05.13.18, кандидат физико-математических наук Ерошкина, Татьяна Васильевна

Специальность ВАК РФ 05.13.18
Количество страниц 103

Скачать автореферат
Читать автореферат

Оглавление диссертации кандидат физико-математических наук Ерошкина, Татьяна Васильевна

Обозначения и соглашения.

Цель и задачи исследования

Ограничения на классы решений.

Историография и общая характеристика работы.

Введение диссертации (часть автореферата) на тему «Математическое моделирование напряженного состояния неоднородных цилиндрических стержней»

Научная новизна результатов работы.18

Теоретическая и практическая ценность работы.19

Краткое содержание диссертации .20

Основные результаты, выносимые на защиту.24

1 Математические модели напряженного состояния сплошного стержня с поперечным менее прочным однородным слоем при осевой нагрузке 26

1.1 Математическая модель НС МП поперечного слоя при ГППС 27

1.2 Исследование НС МП слоя в окрестности свободной границы методом характеристик.31

1.2.2 Система характеристических уравнений и ее приближенное интегрирование. 32

1.2.3 Вычисление напряжений на контактной границе в окрестности свободной границы в критический момент на-гружения (решение задачи сопряжения для напряжений на контактной границе). 35

1.2.4 Вычисление координаты точки ^Р в критический момент нагружения. 39

1.3 Полное описание и исследование математических моделей

НС МП слоя при ГРП (статически квазиопределимая задача) 41

1.3.1 Введение. 41

1.3.2 Исследование модели, когда касательные напряжения изменяются линейно поперек МП слоя. 43

1.3.3 Исследование модели, когда касательные напряжения изменяются линейно в радиальном направлении . 49

1.4 Математическая модель на основе полной системы уравнений

НДС МП слоя . 51

1.4.1 Вычисление касательных напряжений. 51

1.4.2 Вычисление скоростей смещений. 53

1.5 Вычисление критической нагрузки. 54

1.5.1 Введение. 54

1.5.2 Вычисление критической нагрузки, когда касательные напряжения изменяются линейно в радиальном направлении. 55

1.5.3 Вычисление критической нагрузки, когда касательные напряжения изменяются линейно поперек МП слоя 58

1.6 Гипотеза параболических сечений. 62

1.6.1 Математическая постановка задачи . 62

1.6.2 Вычисление компонент тензора напряжений и скоростей смещений при гипотезе параболических сечений 63

2 Математические модели НС МП слоя с переменной прочностью по толщине 69

2.1 Постановка задачи. 69

2.2 Исследование НС неоднородного МП слоя в окрестности свободной границы методом характеристик. 72

2.2.1 Система уравнений пластического равновесия в инвариантной форме . 72

2.2.2 Приближенное интегрирование системы уравнений пластического равновесия, записанной в инвариантной форме. 74

2.3 Вычисление напряжений на контактной границе в критический момент нагружения (решение задачи сопряжения для напряжений па контактной границе). 77

2.3.1 Вычисление касательных напряжений на контактной границе. 77

2.3.2 Вычисление координаты точки Р. 81

2.4 Исследование математических моделей НС МП слоя с пере- ‘ менной по толщине прочностью в окрестности оси стержня при ГРП. 82

2.4.1 Классификация условий разрешимости уравнения, определяющего касательные напряжения. 82

2.4.2 Исследование НС МП слоя с переменной по толщине прочностью, когда касательные напряжения изменяются линейно в радиальном направлении. 84

2.5 Вычисление критической нагрузки. 88

Обозначения и соглашения

В работе используются обозначения, принятые в механике твердого тела, а также: ус — относительная толщина слоя; индекс «*» (вверху) — значение величины в критический момент; индекс «БП» («МП») вверху указывает на отношение данной величины к более прочной (менее прочной) части соединения (для снижения громоздкости формул индекс «МП» в некоторых случаях не ставится).

В работе приняты следующие сокращения.

ММ — математическая модель (математические модели);

ЗТВ — зона термического влияния; ОМ — основной металл;

НС — напряженное состояние; НДС — напряженно-деформированное состояние;

МП — менее прочный; БП — более прочный;

ПН — пластическая неустойчивость; ЛПД — локализация пластических деформаций;

ГППС — гипотеза плоских поперечных сечений; ГПрС — гипотеза продольных сечений; ГРП — гипотеза разделения переменных; МГ — мультипликативная гипотеза.

Во многих случаях, когда это не может привести к разночтениям, касательные напряжения тгг обозначаются буквой т без индексов.

В диссертации рассматриваются математические модели НС сплошного круглого стержня из упрочняемого материала, содержащего поперечный слой из МП материала, при монотонном статическом нагружении осевой силой, на этапе пластического деформирования слоя.

Изменение геометрических размеров (во всех направлениях) рассматриваемого участка стержня при возрастании осевой нагрузки приводит к приращению напряжений на данном участке, которые компенсируются за счет упрочнения материала стержня, и в этом случае пластическое деформирование протекает устойчиво. Однако упрочнение происходит по закону, который на стадии развитых пластических деформаций можно аппроксимировать монотонно возрастающей выпуклой вверх функцией, а рост напряжений за счет изменения геометрии конструкции в зависимости от деформаций идет по экспоненте, скорость роста которой выше скорости роста выпуклой вверх функции. Следовательно, при возрастании осевой нагрузки должен наступить такой момент, когда упрочнения материала оказывается недостаточно для нейтрализации роста напряжений, связанного с изменением формы. В этот момент, определяемый равенством дифференциалов двух указанных зависимостей, происходит «потеря общей пластической устойчивости, т. е. начинается деформирование материала с неконтролируемой скоростью при постоянных или уменьшающихся внешних нагрузках» [39], т. е. наступает момент ПН. Заметим, что ПН деформирования стержня приводит сразу к ЛПД (образованию шейки), в отличие от оболочки, нагруженной внутренним давлением, когда начало неустойчивого деформирования может происходить существенно раньше начала образования шейки.

Рассматривается стадия нагружения, когда ОМ деформируется пластически устойчиво, а материал МП слоя достиг момента начала ПН и деформируется без увеличения внешней нагрузки, т. е. находится в состоянии предразрушения (это состояние в работе называется критическим). В этот момент за счет контактного упрочнения в МП слое, в случае относительно небольшой механической неоднородности между ОМ и МП слоем, происходит вовлечение в неустойчивое пластическое течение приконтактных участков в ОМ. Для исследования состояния ПН, близкого по свойствам к идеальной пластичности, в качестве модельной ситуации рассматривается стержень из идеального упруго-пластического материала на стадии деформирования, когда МП слой прошел предел текучести, а ОМ работает упруго, за исключением приконтактных участков, также перешедших в пластическое состояние.

В диссертации рассматриваются:

1. Математические модели НДС поперечного однородного МП слоя прямоугольного сечения в сплошном стержне из упрочняемого материала, при нагружении стержня осевой силой;

2. Математические модели НДС поперечного неоднородного МП- слоя прямоугольного сечения сплошного стержня из упрочняемого материала при нагружении стержня осевой силой.

Все рассматриваемые задачи предполагаются осесимметричными, т. е. НДС и геометрия объекта изучения инвариантны относительно вращения вокруг некоторой оси (в данном случае, оси стержня). НДС пластической среды при осесимметричной деформации определяется, как известно [30, 35], системой уравнений (знак «тильда» указывает на наличие размерности у данной величины) даг drrz

Список литературы диссертационного исследования кандидат физико-математических наук Ерошкина, Татьяна Васильевна, 2010 год

1. Аннин Б.А., Бытев С.И., Сенатов С.И. Групповые свойства уравнений упругости и пластичности.-Новосибирск: Наука, 1985.-140 с.

2. Анцупов В.П., Кадченко С.И., Соловьев В.В. Определение напряженно-деформированного состояния и основных характеристик поверхностного слоя при упрочнении цилиндрических изделий щетками // Межвуз. сборник трудов. Магнитогорск, МГПИ, 1993. -С. 102 — 112.

3. Бакши O.A. Механическая неоднородность сварных соединений: Автореф. дисс. . докт. техн. наук / МВТУ им. Н.Э. Баумана. -Москва, 1967. 35 с.

4. Бакши O.A. Механическая неоднородность сварных соединений. -Челябинск: Изд-во Челяб. политехи, ин-та, 1981. Ч. 1. — 57 с.

5. Бакши O.A. Механическая неоднородность сварных соединений. -Челябинск: Изд-во Челяб. политехи, ин-та, 1981. Ч. 2. — 56 с.

6. Бакши O.A., Шатов A.A. О напряженном состоянии и деформации твердого металла в сварных соединениях с твердой и мягкой прослойками // Свароч. пр-во. 1966. — №5. — С. 17-20.

7. Бакши O.A. О напряженном состоянии мягких прослоек в сварных соединениях при растяжении (сжатии) // Сб. науч. тр. ЧПИ: Вопросы свароч. пр-ва. Челябинск: Изд-во Челяб. политехи, ин-та, 1965. — Вып. 33. — С. 5-26.

8. Бакши O.A., Качанов J1.M. О напряженном состоянии пластической прослойки при осесимметричной деформации // Изв. АН СССР. Механика. 1965. — №2. — С. 134-137.

9. Бакши O.A., Шрон Р.З. О расчетной оценке прочности сварных соединений с мягкой прослойкой // Свароч. пр-во. 1971. — №3. -С. 3-5.

10. Бакши O.A. Об учете фактора механической неоднородности сварных соединений при испытании на растяжение // Свароч. пр-во. -1985. №7. — С. 32-34.

11. Бакши O.A., Шрон Р.З. Прочность при статическом растяжении сварных соединений с мягкой прослойкой // Сварочное производство. 1962. -№5. — С. 6-10.

12. Бриджмен П. Исследование больших пластических деформаций и разрыва. М.: Изд-во иностр. лит., 1955. — 444 с.

13. Бродский А.Я., Евстратов Г.И. Сварка арматуры железобетонных конструкций на строительной площадке. М.: Стройиздат, 1978. -271 с.

14. Воронцов А.Л. Изменение геометрии цилиндрической заготовки при осадке с контактным трением // Вестн. машиностроения. -2009. № 7. — С. 68-75.

15. Даунис М.А., Браженас А.П. Сопротивление деформированию и разрушению механически неоднородных сварных соединений при однократном нагружении// Проблемы прочности. -1979. №12. -С. 53-58.

16. Дильман B.JL, Остсемин A.A. К анализу напряженного состояния в шейке образца при растяжении // Завод, лаборатория. 1998. -№1. — С. 47-49.

17. Дильман B.JI. Математические модели напряженного состояния неоднородных тонкостенных цилиндрических оболочек. Челябинск: Изд-во ЮУрГУ, 2007. — 202 с.

18. Дильман В.Л., Остсемин A.A. Напряженное состояние и прочность сварных соединений с механической неоднородностью // Свароч. пр-во. 1998. — №5. — С. 15-17.

19. Дильман B.JL, Остсемин A.A. Напряженное состояние и прочность сварных швов труб большого диаметра // Химич. и нефтегаз. машиностроение. 1998. — №4. — С. 16-20.

20. Дильман B.JL, Остсемин A.A. Напряженное состояние пластического слоя с переменной прочностью по толщине // Изв. РАН. Механика твердого тела. 2000. — № 1. — С. 141-148.

21. Дильман B.JL, Остсемин A.A. Напряженное состояние и статическая прочность пластичной прослойки при плоской деформации // Проблемы машиностроения и надежности машин. 2005. — №4. -С. 38-48.

22. Дильман В.Л., Остсемин A.A. О напряженно-деформированном состоянии пластического кольца при растяжении // Изв. РАН. Механика твердого тела. 2002. — № 2. — С. 109-120.

23. Дильман В.JI., Остсемин A.A. О напряженно-деформированном состоянии при растяжении пластического слоя с двумя осями симметрии // Изв. РАН. Механика твердого тела. 2001. — №6. — С. 115-124.

24. Дильман B.JI. О некоторых математических моделях напряженного состояния пластической среды при осесимметричной деформации // Вест. ЮУрГУ. Серия «Математика, физика, химия». 2005. -№2. — С. 20-25.

25. Дильман B.JI. О приближенном решении системы уравнений напряженно-деформированного состояния пластического кольца при растяжении // Изв. Челяб. науч. центра. 2001. — Вып. 3. — С. 1-5.

26. Дильман B.JI. Об одном приближенном решении системы уравнений напряженно-деформированного состояния пластического слоя в случае плоской деформации // Изв. Челяб. науч. центра. 2001.- Вып. 4. С. 1-4.

27. Дильман B.JI. Приближенное решение системы уравнений напряженно-деформированного состояния для пластического кольцевого слоя // Обозрение прикл. и пром. математики. 2000.- Т. 7, вып. 2. С. 340.

28. Ивлев Д.Д., Ершов JI.B. Метод возмущений в теории упругопла-стических деформаций. М.: Наука, 1978. — 196с.

29. Ивлев Д.Д. Теория идеальной пластичности. -М.: Наука, 1966. -231 с.

30. Ильюшин A.A. Пластичность М.: Изд-во АН СССР, 1963. — 271 с.

31. Ишлинский А.Ю., Ивлев Д.Д. Математическая теория пластичности. М.: Физматлит, 2001. — 704 с.

32. К вопросу о расчетной прочности составных образцов с мягкой прослойкой при статическом растяжении/ A.B. Гурьев, В.П. Багмутов, Ю.Д. Хесин, JI.B. Бойков // Проблемы прочности. 1973. — №1. -С. 9-13.

33. Качанов JI.M. Основы теории пластичности. М.: Наука, 1969. -420 с.

34. Качанов JI.M. К задаче о деформации пластического слоя// ДАН СССР. 1954. — Т. XCVI, №2. — С. 249-252.

35. Качанов JI.M. О напряженном состоянии пластической прослойки // Изв. АН СССР. Отд. техн. наук. Механика и машиностроение. -1962. -№5. С. 63-67.

36. Качанов JI.M., Немчинский A.JI. Об одном способе определенния сопротивления отрыву // Физика металлов и металловедение. -1957. Том 4, вып. 1. — С. 151-160.

37. Ковальчук Г.И. К вопросу о потери устойчивости пластического деформирования оболочек // Проблемы прочности. 1983. — №5. — С. 11-16.

38. Когут Н.С., Шахматов М.В., Ерофеев В.В. Несущая способность сварных соединений. Львов: Свит, 1991. — 184 с.

39. Кузнецов А.И. Задача о неоднородном пластическом слое // Archiwum mechaniki stosowanej. 1960. — Т. 12, №2. — С. 163-172.

40. Махутов H.A. Деформационные критеритерии разрушения и расчет элементов конструкций на прочность. М.: Машиностроение, 1981. — 272 с.

41. Надаи А. Пластичность и разрушение твердых тел. М.: Изд-во иностр. лит., 1954. — 494 с.

42. О разрушении высокопрочных сталей при сварке / A.M. Макара, В.А. Саржевский, Н.Е. Протосей и др. // Свароч. пр-во. 1968. -№8. — С. 1-5.

43. Олыпак В., Рыхлевский Я., Урбановский В. Теория пластичности неоднородных тел. М.: Мир, 1964. — 156 с.

44. Остсемин A.A., Дильман B.JI. О сжатии пластического слоя двумя шероховатыми плитами // Проблемы прочности. 1990. — №7. — С. 107-113.

45. Остсемин A.A., Дильман B.JI. Статическая прочность и напряженное состояние механически неоднородных стыковых сварных соединений с Х-образной разделкой кромок // Автомат, сварка. 2005. -№11. — С. 22-25.

46. Пластичность и разрушение / B.JI. Колмогоров, A.A. Богатов, В.А. Мигачев и др. М.: Металлургия, 1977. — 331 с.

47. Прандтль JI. Примеры применения теоремы Генки к равновесию пластических тел // Теория пластичности / под ред. Ю.Н. Работ-нова. М.: Изд-во иностр. лит., 1948. — С. 103-113.

48. Предельное состояние деформируемых тел и горных пород / Д.Д. Ивлев, JI.A. Максимова, Р.И. Непершин, Ю.Н. Радаев, С.И. Сенатов, Е.И. Шемякин. М.: Физматлит, 2008. — 832 с.

49. Смирнов-Аляев Г.А. Механические основы пластической обработки металлов. Л.: Машиностроение, 1968. — 272 с.

50. Соколовский В.В. Теория пластичности. М.: Высшая школа, 1969.- 608 с.

51. Теория ковки и штамповки / Е.П. У иксов, У. Джонсон, В. Л. Колмогоров и др. М.: Машиностроение, 1992. — 720 с.

52. Теория обработки металлов давлением (вариационные методы расчета усилий и деформаций) / И.Я. Тарновский, Д.А. Поздеев, О.А. Ганаго и др. М.: Металлургиздат, 1963. — 672 с.

53. Теория пластических деформаций металлов / Е.П. Унксов, У. Джонсон, В.Л. Колмогоров и др. М.: Машиностроение, 1983. -598 с.

54. Томленов А.Д. Теория пластического деформирования металлов. -М.: Металлургия, 1972. 408 с.

55. Томсен Э., Янг Ч., Кобаяши Ш. Механика пластических деформаций при обработке металлов. -М.: Машиностроение, 1969.- 502 с.

56. Унксов Е.П. Инженерная теория пластичности. М.: Машгиз, 1959.- 328 с.

57. Харченко Г.К. Прочность соединений с тонкой мягкой прослойкой. // Автомат, сварка. 1968. — №5. — С. 31-33.

58. Хилл Р. Математическая теория пластичности. М.: Государств, изд-во технико-теоретич. литературы, 1956. — 407 с.

59. Христианович С.А., Шемякин Е.И. К теории идеальной пластичности // Инж. журн. Механ. твчрдого тела. 1967 — № 4. — С. 58-69.

60. Шахматов М.В., Ерофеев В.В., Остсемин А.А. О некоторых особенностях метода линий скольжения при решении осесимметричных задач теории пластичности // Проблемы прочности. 1985. — №3.- С. 88-94.

61. Шахматов М.В., Храмова Л.И., Бакши О.А. Влияние геометрических парамеров механически неоднородных сварных соединений арматуры железобетона на их предельную несущую способность // Свароч. пр-во. 1986. — №6. — С. 28-30.

62. Шахматов М.В., Ерофеев В.В. Напряженное состояние и прочность сварных соединений с переменными механическими свойствами металла мягкого участка // Свароч. пр-во. 1982.- №3. — С. 6-7.

63. Biljavsky L.S., Kadchenko S.I. Application of the protective coating by frictional-mecanical metod for increasing the durability of machines and materials // Journal for Technology of Plasticity. 1996. — V. 21.- P. 1-2.

64. Dilman V.L., Ostsemin A.A. Strenght of straight-seam pipes in transmission gas and oil pipelines // Welding International. 2001. -V. 15(7).-P. 557-562.

65. Prandtl L. Beispiele der Anwendung des Hencky’s Theorems zum Gleichgewicht der plastischen Körper// ZAMM 1923. — Bd, 3. — №6. — S. 401-406.

66. Satoh К., Toyoda M. Joint strength of heavy plastics with lower strength weld metal // Welding Journal. Sept. — 1975. — №9. — P. 311-319.

67. Satoh K. Size effect on static tensile properties of welded joints including of soft interlaver// Journal Jap. Welding Soc. 1968. — 37. -№ 11. — P. 242-249.

68. Дильман В.JI., Ерошкина Т.В. Об одной модели, описывающей напряженное состояние в круглом стержне // Обозрение приклад, и пром. математики. 2004. — Т. И, вып. 2. — С. 793-794.

69. Дильман В.Л., Ерошкина Т.В. Об одной математической модели напряженного состояния пластического слоя при плоской деформации // Вест. ЮУрГУ. Серия «Математика, физика, химия».2005. Вып. 6. — № 6. — С. 19-23.

70. Дильман В.Л., Ерошкина Т.В. Математические модели осесиммет-ричного напряженного состояния при гипотезе разделения переменных для касательных напряжений // Изв. Челяб. науч. центра.2006.-Вып. 2(32).-С. 1-4.

71. Дильман В.Л., Ерошкина Т.В. Напряженное состояние продольной мягкой прослойки, с сечением в форме кольцевого сектора, в тонкостенной цилиндрической оболочке // Обозрение прикл. и пром. математики. 2006. — Т. 13, вып. 4. — С. 637-638.

72. Дильман В.Л., Ерошкина Т.В. Математические модели напряженного состояния пластического слоя с сечением в форме кольцевого сектора // Вест. ЮУрГУ. Серия «Математика, физика, химия». -2006. Вып. 7. — №7(62). — С 13-21.

73. Ерошкина, Т.В. Напряженное состояние поперечной мягкой прослойки в растягиваемом круглом стержне при гипотезе параболических сечений // Обозрение прикл. и пром. математики. 2007. -Т. 14, вып. 1. — С. 109-110.

74. Ерошкина Т.В. Анализ математических моделей напряженно-деформированного состояния продольной мягкой прослойки, с сечением в форме кольцевого сектора, в цилиндрической оболоке // Обозрение прикл. и пром. математики. 2007. — Т. 14, вып. 4. — С. 708-709.

75. Ерошкина Т.В. Напряженное состояние и прочность Х-образной мягкой поперечной прослойки в круглом стержне // Обозрение прикл. и пром. математики. 2008. — Т. 15, вып. 3. — С. 469-470.

76. Ерошкина Т.В. Напряженное состояние мягкой поперечной прослойки в круглом стержне // Дифференциальные уравнения и смежные проблемы: тр. междунар. конф. (24 28 июня 2008 г., Стерлитамак). — Уфа: Гилем, 2008. — Т. III. — С. 201-205.

77. Дильман В.Л., Остсемин A.A., Ерошкина Т.В. Прочность механически неоднородных сварных соединений стержней арматуры // Вестник машиностроения. 2008. — № 9. — С. 13-17.

78. Ерошкина Т.В. Особенности моделирования предельной осевой нагрузки неоднородного сплошного стержня // Обозрение прикл. и пром. математики. 2009. — Т. 16, вып. 2. — С. 325-326.

79. Ерошкина Т.В. Математические модели напряженного состояния неоднородного сплошного цилиндра при его растяжении // Тр. ма-темат. центра им. Лобачевского. Казань: Изд-во КГУ, 2009. — Т. 38. — С. 121-123.

80. Дильман В.Л., Ерошкина Т.В. Исследование математических моделей напряженного состояния неоднородного поперечного слоя в круглом стержне // Вест. ЮУрГУ. Серия «Математическое моделирование и программирование». 2009. — Вып. 4. — №37(170). — С. 65-77.

Обратите внимание, представленные выше научные тексты размещены для ознакомления и получены посредством распознавания оригинальных текстов диссертаций (OCR). В связи с чем, в них могут содержаться ошибки, связанные с несовершенством алгоритмов распознавания. В PDF файлах диссертаций и авторефератов, которые мы доставляем, подобных ошибок нет.

Digital Science & Education LP, 85 Great Portland Street, First Floor, London, United Kingdom, W1W 7LT

источники:

http://cyberleninka.ru/article/n/o-nekotoryh-matematicheskih-modelyah-napryazhennogo-sostoyaniya-plasticheskoy-sredy-pri-osesimmetrichnoy-deformatsii

http://www.dissercat.com/content/matematicheskoe-modelirovanie-napryazhennogo-sostoyaniya-neodnorodnykh-tsilindricheskikh-ste

Математическая модель напряженного состояния это система уравнений

Математическая модель напряженно-деформированного состояния тела

О некоторых математических моделях напряженного состояния пластической среды при осесимметричной деформации Текст научной статьи по специальности « Физика»

Аннотация научной статьи по физике, автор научной работы — В. Л. Дильман

Похожие темы научных работ по физике , автор научной работы — В. Л. Дильман

Текст научной работы на тему «О некоторых математических моделях напряженного состояния пластической среды при осесимметричной деформации»

Оглавление диссертации кандидат физико-математических наук Ерошкина, Татьяна Васильевна

Рекомендованный список диссертаций по специальности «Математическое моделирование, численные методы и комплексы программ», 05.13.18 шифр ВАК

Математическое моделирование и исследование процессов обработки металлов давлением 1998 год, доктор технических наук Кудюров, Лев Владимирович

Задачи нелинейного деформирования элементов конструкций 1999 год, доктор физико-математических наук Волчков, Юрий Матвеевич

Введение диссертации (часть автореферата) на тему «Математическое моделирование напряженного состояния неоднородных цилиндрических стержней»

Похожие диссертационные работы по специальности «Математическое моделирование, численные методы и комплексы программ», 05.13.18 шифр ВАК

Математические модели нелинейных распределенных систем в виде пластинчатых конструкций 2003 год, доктор физико-математических наук Крысько, Антон Вадимович

Список литературы диссертационного исследования кандидат физико-математических наук Ерошкина, Татьяна Васильевна, 2010 год