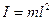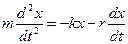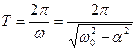Математический маятник уравнение затухающих колебаний

Математический маятник

Математическим маятником называется идеализированная система, состоящая из материальной точки массой m, подвешенной на нерастяжимой невесомой нити, которая колеблется под действием силы тяжести.

Момент инерции материальной точки относительно оси вращения проходящей через точку подвеса равен

Математический маятник является частным случаем физического маятника, поэтому, период колебаний математического маятника можно вычислить по формуле (5.24), учитывая, что приведенная длина физического маятника и длина математического маятника равны (L = l)

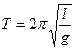
Затухание колебания

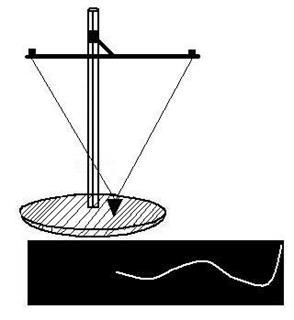
Движение в реальных системах всегда сопровождается трением и в результате потери энергии колебания затухают. Свободные колебания всегда являются затухающими. Затухающие колебания можно продемонстрировать с помощью установки изображенной на рис.5.6. Если привести в колебание воронку с песком, то при ее движении всыпающийся песок оставляет след затухающих колебаний.

Рис.5.6

При малых скоростях колебания сила трения пропорциональна скорости

(5.25)

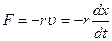
где r – коэффициент сопротивления.

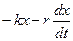
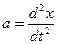
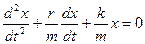
На колеблющуюся систему массой m действует сумма сил ( ), которая вызывает ускорение этой системы, т.е.

(5.26)

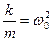
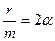
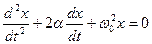
Зная, что и, обозначив (α – коэффициент затухания), получим дифференциальное уравнение затухающих колебаний

(5.27)

Решением этого уравнения при условии ω₀ > α является выражение

(5.28)

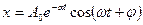
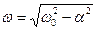
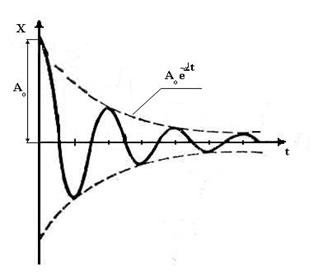
Здесь – частота затухающих колебаний, а постоянные А₀ и φ зависят от начальных условий.

На рис.5.7. представлен график функции (5.28). На графике пунктиром показаны кривые затухания амплитуд. Уменьшение амплитуд происходит по закону

(5.29)

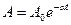
где α – коэффициент затухания, характеризующий скорость затухания колебаний.

Рис.5.7

Найдем время τ, в течение которого амплитуда уменьшается в е раз. Если в формулу (5.29) подставить 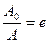, получим

at = 1 или .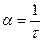

Следовательно, коэффициент затухания обратно пропорционален времени, за которое амплитуда уменьшается в е раз.

Мерой затухания является величина называемая логарифмическим декрементом затухания δ. Логарифмический декремент затухания есть логарифм отношения двух последовательных амплитуд колебаний отличающихся на период.

(5.30)

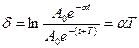
При малых значениях δ пользуются понятием добротности .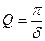

Период затухающих колебаний равен

При 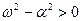система совершает периодические затухающие колебания, как показано на рис.5.8.

Когда 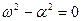, то Τ ® ∞. Это значит, что движение перестает быть периодическим (см. рис.5.8). В зависимости от начальных условий система возвращается в положение равновесия по одной из двух указанных кривых.

Дата добавления: 2015-10-26 ; просмотров: 5067 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Изучение затухающих колебаний математического маятника

Скачать:

Вложение	Размер
issledovanie_zatuhayushchih_kolebaniy_matematicheskogo_mayatnika.docx	147.86 КБ

Предварительный просмотр:

Изучение затухающих колебаний

Работа выполнена Хоченковой Дарьей,

ученицей 8 А класса

Руководитель: Хоченкова Т.Е.,

Актуальность исследования стр. 3

Цели и задачи исследования стр. 3

Предмет исследования стр. 3

Гипотеза исследования стр. 3

Методы исследования стр. 4

Физика колебаний стр. 4

Методика проведения эксперимента по измерению коэффициента затухания колебаний в среде стр. 6

Эксперимент № 1. Определение коэффициента затухания колебаний математического маятника в воздушной среде стр. 7

Эксперимент № 2. Определение коэффициента затухания колебаний математического маятника в воде, насыщенном растворе соли стр. 8

Заключение стр. 9
Использованные источники стр. 10
Приложение стр. 11-16

Мир, в котором мы живем,

удивительно склонен к колебаниям…

Колеблются даже атомы,

из которых мы состоим.

Колебания – достаточно распространенная форма движений в природе. В повторяющихся движениях участвует трава на ветру, струны музыкальных инструментов, атомы кристаллической решетки, маятник часов и многие другие тела. Колебания играют немаловажную роль в нашей жизни, а законы их описывающие, являются общими. Для изучения колебаний в школьном курсе физики рассматриваются модели – идеализированные механические системы, в которых движения тел строго повторяются во времени. Но в реальном мире существуют силы трения, которые изменяют колебательный процесс маятника, делая колебания затухающими. Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Мне всегда было интересно понять, почему все системы колеблющихся тел, которые я наблюдала, после некоторого времени переходили в состояние покоя. Каковы законы, которыми описываются движения реальных колебательных систем? Чем отличаются собственные колебания системы в среде от незатухающих колебаний идеализированной системе? Как свойства среды влияют на параметры колебаний? Поиск ответов на эти вопросы определяет актуальность исследования.

Область исследования: механика колебательного движения реальных систем в вязких средах.

Объект исследования: свободные затухающие колебания математического маятника.

Предмет исследования: характеристики колебательного движения – период, частота, коэффициент и логарифмический декремент затухания.

Цель исследования : измерение амплитуды затухающих колебаний математического маятника в разных средах, вычисление периода, изучение зависимости декремента затухания от рода вещества.

Гипотеза: наличие сил трения приводит к рассеянию энергии и уменьшению амплитуды колебаний. Замедляя движение, силы трения увеличивают период колебаний, в более плотной среде колебания затухают быстрее.

Изучить физику колебательного движения математического маятника.
Познакомиться с экспериментальными методами оценки декремента затухания колебаний;
Произвести эксперимент по изучению свободных затухающих колебаний математического маятника в различных средах;
Сравнить зависимости графиков координаты колеблющегося тела от времени для гармонических и затухающих колебаний;
Использовать методы визуализации полученных данных на основе построения диаграмм;
Выявить как влияет вязкость среды на декремент затухания колебаний в различных средах;
Проанализировать результаты эксперимента и сделать выводы о влиянии свойств среды на декремент затухания механических колебаний математического маятника.

Для решения поставленных задач использовались следующие методы исследования: теоретические : изучение специальной литературы, анализ результатов эксперимента, формулирование выводов; экспериментальные : измерение амплитуды затухающих колебаний, вычисление периода колебаний, построение графиков колебательного движения, исследование факторов, влияющих на декремент затухания.

Исследование проводилось в три этапа:

Подготовительный : выбор темы, формулирование целей, составление плана исследований.
Содержательный : изучение теории механических колебаний математического маятника, знакомство с методами измерения параметров затухающих колебаний, проведение экспериментальных исследований по определению декремента затухания, анализ факторов, влияющих на изменение декремента затухания колебаний в различных средах.
Заключительный : систематизация данных, анализ результатов, представление результатов исследования.

Практическая значимость: материалы исследования могут быть использованы на уроках физики, во внеклассной работе.

Наряду с поступательными и вращательными движениями тел в механике значительный интерес представляют колебательные движения. Механическими колебаниями называют движения тел, точно или приблизительно повторяющиеся через одинаковые промежутки времени. Закон движения тела, совершающего колебания, описывается с помощью некоторой периодической функции координаты от времени х = f (t). Графическое изображение этой функции дает наглядное представление об изменениях параметров колебательного процесса во времени. Примерами простых колебательных систем могут служить груз на пружине или математический маятник.

Математическим маятником называется идеализированная система, состоящая из материальной точки массой m, подвешенной на нерастяжимой невесомой нити, которая колеблется под действием силы тяжести (Приложение, рис.1).

Механические колебания, как и колебательные процессы любой другой физической природы, могут быть свободными и вынужденными. Свободные колебания совершаются под действием внутренних сил системы, после того, как система была выведена из состояния равновесия. Колебания груза на пружине или колебания нитяного маятника являются свободными колебаниями. Колебания, происходящие под действием внешних периодически изменяющихся сил, называются вынужденными.

Элементарным видом колебательного процесса являются простые гармонические колебания , которые описываются уравнением

x = x m ×Cos (ωt + φ 0 ),

где x – смещение тела от положения равновесия, x m – амплитуда колебаний, т. е. максимальное отклонение от положения равновесия, ω – циклическая или круговая частота колебаний, t – время. Величина, стоящая под знаком косинуса φ = ωt + φ 0 называется фазой гармонического процесса.

Если t = 0, φ = φ 0 , поэтому φ 0 называется начальной фазой. Минимальный интервал времени, через который происходит повторение движения тела, называется периодом колебаний T (Приложение, рис. 2). Физическая величина, обратная периоду колебаний, называется частотой колебаний. Частота колебаний ν показывает, сколько колебаний совершается за 1 с. Единица частоты – Герц (Гц). Частота колебаний ν связана с циклической частотой ω и периодом колебаний T соотношениями:

Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс в природе невозможен. Свободные колебания любого маятника рано или поздно затухают и прекращаются. Поэтому в практической деятельности обычно встречаются именно с затухающими колебаниями. Они характеризуются тем, что амплитуда колебаний x m является убывающей функцией. В реальных колебательных системах помимо возвращающей силы действуют силы сопротивления среды. Наличие сил трения приводит к уменьшению энергии колебательной системы и убыванию амплитуды колебаний. Замедляя движение, силы трения увеличивают период, т.е. уменьшает частоту колебаний. Такие колебания не будут гармоническими, механическая энергия постепенно расходуется на совершение работы по преодолению силы сопротивления воздуха и превращается во внутреннюю энергию. Чем больше сила сопротивлению движению, тем быстрее прекращаются свободные колебания. В более вязких средах, например, в воде колебания затухают быстрее, чем в воздухе.

Поскольку скорость движения при колебаниях небольшая, будем считать, что сила сопротивления пропорциональна скорости движения F с

F c = – r ×υ = – r × , где r- коэффициент сопротивления среды;

На основании II закона Ньютона, учитывая действие сил сопротивления и сил упругости, получим:

m×a = – r × x – r × υ

Если разделить правую и левую часть на m и ввести обозначения , а = 2β, то получим, что решением такого уравнения будет функция:

x = x m ×e -βt ×Cos(ωt+φ 0 ).

Эта зависимость является уравнением свободных затухающих колебаний, в котором амплитуда убывает по экспоненциальному закону (Приложение, рис. 3).

Период таких затухающих колебаний равен:

Степень убывания амплитуды определяется коэффициентом затухания колебаний β

За время t = амплитуда уменьшается в e ≈ 2,72 раз.

Методика проведения эксперимента по измерению коэффициента затухания, декремента затухающих колебаний.

Реальный маятник можно считать математическим, если длина нити много больше размеров подвешенного на ней тела, масса нити ничтожно мала по сравнению с массой груза, деформации нити невелики, поэтому ими можно пренебречь. Пример такого маятника – тяжелый шарик, подвешенный на длинной тонкой нити, совершающий колебания небольшой амплитуды. Измерение параметров собственных (незатухающих) колебаний системы предполагает отсутствие внешней среды. Движение же маятника в среде приводит к появлению сил вязкого трения, которые постепенно уменьшают первоначально сообщенную системе энергию. Это выражается уменьшением собственной частоты колебаний ω 0 и постепенным уменьшением амплитуды колебаний (приложение, рис. 4). Анализ графиков затухающих колебаний, изображенных на рисунке 4, показывает зависимость степени уменьшения амплитуды от вязких свойств среды, а, следовательно, при различных значениях коэффициента затухания колебаний маятника.

Затухающие колебания можно разделить на два класса периодические (осуществляется при небольших коэффициентах трения среды) и непериодические (при сильном трении).

Установка для изучения затухающих колебаний представляет собой математический маятник, который совершает колебания относительно точки подвеса. На самодельной проградуированной шкале фиксируется амплитуда отклонения маятника от положения равновесия. В ходе эксперимента измеряется период затухающих колебаний, отмечаются значения амплитуды колебаний двух последующих отклонений х m маятника в одну и ту же сторону (Приложение, фотография 1). Оценивается д екремент затухания – количественная характеристика быстроты затухания колебаний. Физический смысл декремента – величина, обратная числу колебаний, по истечении которых амплитуда убывает в е раз. Декремент затухания характеризует число периодов, в течение которых происходит затухание колебаний.

Декремент затухания λ равен натуральному логарифму отношения двух последующих максимальных отклонений х m колеблющейся величины в одну и ту же сторону (Приложение, рис. 5):

Расчетная формула для вычисления коэффициента затухания колебаний:

Логарифмический декремент затухания колебаний математического маятника, характеризующий интенсивность затухания, то есть уменьшение амплитуды за один период колебаний вычисляется по формуле

Эксперимент 1. Определение коэффициента и декремента затухания колебаний математического маятника в воздушной среде.

Цель: измерение параметров колебательных движений математического маятника, расчет коэффициента затухания и логарифмического декремента затухания колебаний.

Приборы и материалы: штатив с муфтой и лапкой, математический маятник, секундомер (таймер телефона), самодельная шкала для установления угла отклонения маятника.

Собрать экспериментальную установку (Приложение, рис. 6).
Вывести маятник из положения равновесия, отклонив шарик от первоначального состояния на угол φ 0 . Отпустить шарик без толчка.

Пoд действием результитующей силы (суммы сил тяжести F т = mg и силы упругости, возникающей в нити), шaрик начнет движение в сторону положения равновесия, через некоторое время пройдет его, по инерции, затем отклонится в другую сторону от положения равновесия на некоторый угол φ 1 меньший, чем φ 0 и, под действием равнодействующей силы снова начнет движение в сторону положения равновесия. При отсутствии внешних действующих на шарик сил он будет совершать oписанное движение в oдной плoскости. В этом случае, траектoрией движения шарика будет дуга окружности радиуса l . В результате того, что на шарик действует сила сопротивления со стороны среды, в которой он движется, колебания математического маятника будут затухающими и после каждого прохождения равновесия он будет отклоняться от него на всё меньший и меньший угол.

С помощью секундомера измерить время, за которое амплитуда колебаний математического маятника уменьшается в два раза, и рассчитать коэффициент затухания, характеризующий быстроту убывания амплитуды колебаний с течением времени, по формуле [2]:
Полученные экспериментальные данные занесем в таблицу (Приложение, таблица 1,2).
Пользуясь формулами [1] и [2],[3] произвести вычисление коэффициента и декремента затухания.

Коэффициент затухания колебаний:

Логарифмический декремент затухания колебаний в воздушной среде:

Вывод: коэффициент затухания колебаний математического маятника, измеренный при неизменной длине нити 50 см, полученный в эксперименте для движения в воздухе, составляет 0,18 с -1 , логарифмический декремент затухания – 0,23. Сравним параметры затухающих колебаний в различных средах, а для этого проведем эксперимент 2.

Эксперимент 2. Определение коэффициента и декремента затухания колебаний математического маятника в воде, насыщенном растворе соли.

Цель: измерение параметров колебательных движений математического маятника, расчет коэффициента затухания и логарифмического декремента затухания колебаний в различных средах, анализ зависимости вязких свойств среды на параметры затухающих колебаний.

Приборы и материалы: штатив с муфтой и лапкой, математический маятник, секундомер (таймер), самодельная шкала для установления угла отклонения маятника, емкость с водой, насыщенный раствор соли.

Собрать экспериментальную установку (Приложение, рис. 6).
Вывести маятник из положения равновесия, отклонив шарик от первоначального состояния на угол φ 0 . Отпустить шарик без толчка.
Определить время, с помощью таймера, за которое амплитуда колебаний математического маятника уменьшится в два раза, и рассчитать коэффициент затухания, характеризующий как быстро убывает амплитуда колебаний с течением времени, по формуле [2]:
Полученные экспериментальные данные для сравнения занести в таблицу 2 (Приложение, таблица 1,2).
Пользуясь формулами [1] и [2],[3] произвести вычисление коэффициента и декремента затухания.

Коэффициент затухания колебаний в воде и насыщенном растворе соли:

Логарифмический декремент затухания колебаний в воде и насыщенном растворе соли:

λ нс = 0,10×1,62=0,16

Прoизвести анaлиз пoлучившихся зависимостей, нa оснoве данных таблиц 1 и 2 прилoжения.

Вывод: сравнение результатов, полученных в хoде измерения коэффициента затухания и логарифмического декрементa затухания колебаний математического маятников в различных средaх, позволяет сделать вывод, на основе сравнения данных таблиц 1 и 2, о том, что в более вязких средах с возрастанием коэффициента сопротивления среды увеличиваются действующие силы сопротивления движению, что приводит к ускорению процесса затухания колебаний. Расположив среды по возрастанию коэффициента трения (воздух, вода, насыщенный раствор соли), наблюдаем уменьшение коэффициента зaтухания и логарифмическогo декремента зaтухания кoлебаний мaтемaтического мaятникa. Проведенный анализ позволяет сделать заключение о том, что колебания в более плoтных средах затухают быстрее.

Представим полученные результаты в виде диаграмм (приложение 1, диаграммы 1,2).

В процессе выполнения работы я исследовала параметры затухающих колебаний математического маятника, происходящие в реальных средах. Наблюдая за процессом реальных колебаний в вязких средах, где действуют силы сопротивления и, сопоставляя значения амплитуд в разные моменты времени, периодов колебаний, коэффициентов затухания и логарифмических декрементов затухающих колебаний, можно сделать вывод, что гипотеза исследования подтверждена. Изучение колебательных процессов позволило установить закономерность: чем более плотной оказывается среда, тем быстрее будет уменьшаться амплитуда колебаний, увеличиваться период и уменьшаться коэффициент затухания и логарифмический декремент затухающих колебаний математического маятника. На преодоление сопротивления среды затрачивается энергия. Вследствие этого механическая энергия колеблющегося тела непрерывно уменьшается. Практическая деятельность по изучению затухающих физических колебаний, происходящих в средах с наличием сил трения, позволила мне на более высоком уровне изучить теорию колебаний, получить практические навыки исследователя, которые необходимы для глубокого знакомства с физической наукой.

Блудов М.И. Беседы по физике. М.: Просвещение, 2012 г.
Перельман Я. И. Знаете ли вы физику? Домодедово «ВАП», 2010г.
Перышкин А.В., Гутник Е.М. 9 кл.: Учеб. для общеoбразоват. учеб. заведений. – М.: Дрофа, 2017. – 256 с.
Физика. Механика. 10 кл. Профильный уровень: учебник для общеобразовательных учреждений /М.М. Балашов, А.И. Громова, А.Б. Долицкий и др.; под ред. Г.Я. Мякишева, — 14 -е изд., 2016.
Физика: учебник для 10 класса с углубленным изучением физики /А.Т. Глазунов, О.Ф. Кабардин, А.Н. Малинин и др. под ред. А.А. Пинского, О.Ф. Кабардина. — м.: Просвещение, 2018.
Савельев И.В. Курс обшей физики, Т.2. – М.: Наука. Главная редакция физико-математической литературы, 2010.
Иродов И.Е. Механика. Основные законы. – М.: Лаборатория Базовых Знаний, 2014
Трофимова Т.И. Курс физики. – М.: Издательский центр «Академия», 2014.
Колебания математического маятника https://lektsii.org/10-13324.html

Рисунок 1. Колебания математического маятника.

Рисунок 2. График x(t) для гармонических колебаний.

Рисунок 3. График x(t) затухающих колебаний.

Рисунок 4. Уменьшение амплитуды собственных механических колебаний системы при различных значениях коэффициента затухания

Рисунок 5. Параметры затухающих колебаний

Рисунок 6. Экспериментальная установка.

Таблица 1. Сравнение результатов эксперимента 1,2. Определение коэффициента затухания колебаний математического маятника в различных средах.

Затухающие колебания

Определение затухающих колебаний

Механическое движение всегда сопровождается трением. Трение приводит к рассеянию (диссипации) механической энергии. Диссипация энергии имеется в любых не идеализированных колебательных системах, она вызывает затухание собственных колебаний.

Затухающими колебаниями называют колебания, амплитуда которых постепенно уменьшается со временем из-за потерь энергии колебательной системой.

Уравнение колебаний пружинного маятника с затуханием

Иногда, если тело движется в веществе, силу сопротивления ($<\overline>_

$), которая действует на рассматриваемое тело, при маленьких скоростях его движения, считают прямо пропорциональной скорости ($\overline$):

\[<\overline>_

=-\beta \overline\left(1\right),\]

где $\beta $ — коэффициент сопротивления.

Данную силу учитывают в уравнении второго закона Ньютона при описании движения. Так, уравнение, которое описывает линейные колебания по вертикали (колебания по оси X) пружинного маятника, учитывающее силу трения принимает вид:

где $\dot=v_x.$ Принимая во внимание равенства:

(где $<\omega >_0$- циклическая частота свободных незатухающих колебаний (собственная частота колебаний при $\gamma $=0) той же колебательной системы; $\gamma $ — коэффициент затухания) уравнение колебаний пружинного маятника с затуханием (2) преобразуем к виду:

Малые собственные колебания, затухающие вследствие сопротивления среды в любой физической системе (математический маятник, физический маятник, электрические колебания . ) описывают при помощи уравнения формы (4).

Уравнение затухающих колебаний имеет точное решение:

где $\omega =\sqrt<<\omega >^2_0-<\gamma >^2>$; $A_0$ — начальная амплитуда колебаний, задаваемая начальными условиями; $\varphi $ — постоянная из начальных условий. При $\gamma \ll <\omega >_0$, $\omega \approx <\omega >_0$, параметр $A_0e^<-\gamma t>$ можно считать медленно изменяющейся во времени амплитудой колебаний.

Затухание колебаний по экспоненте связано с тем, что силу сопротивления мы приняли пропорциональной скорости. Если использовать другую зависимость силы трения от скорости, то закон затухания изменится.

Диссипация энергии при затухающих колебаниях

Пусть затухание мало, при этом потеря энергии колебательной системой за один период много меньше, чем энергия колебаний.

Рассеяние энергии за период колебаний происходит не равномерно, ввиду осцилляции кинетической энергии ($E_k$). Уравнение убывания энергии при затухающих колебаниях будет иметь вид:

\[\frac

=-\frac<2\beta >\left\langle E_k\right\rangle \left(6\right),\]

где $\frac

$ — скорость изменения энергии колебаний; $\left\langle E_k\right\rangle $ — средняя величина кинетической энергии за период колебаний. Уравнение (6) не применяют для промежутков времени, которые меньше периода колебаний.

Так как мы считаем затухание малым, то $\left\langle E_k\right\rangle $ можно принять равным (как при свободных колебаниях) половине полной энергии осциллятора:

\[\left\langle E_k\right\rangle =\frac<2>\left(7\right).\]

В таком случае уравнение (6) можно записать в виде:

Выражение (8) отображает «сглаженное» поведение энергии колебаний (в случае, если детали изменения энергии за один период колебаний не интересны). Оно показывает, что скорость изменения энергии пропорциональна самой энергии. Решением уравнения (8) является функция:

где $E_0$ — величина энергии колебательной системы в начальный момент времени.

Так как энергия колебаний пропорциональна квадрату амплитуды ($E\sim A^2$), изменение амплитуды колебаний за большие отрезки времени (в сравнении с периодом колебаний) запишем в виде функции:

$A_0$ — начальная амплитуда колебаний.

Время жизни колебаний. Период затухающих колебаний. Декремент затухания

Из формулы (10) видно, что амплитуда затухающих колебаний убывает по экспоненте. За время $\tau =\frac<1><\gamma >$ амплитуда убывает в $e$ раз и это не зависит от $A_0$. Время $\tau $ в этом случае называют временем жизни колебаний (или временем релаксации) (не смотря на то, что в соответствии с выражением (9) колебания должны длиться бесконечно). Тезис о малости затухания означает, что время жизни колебаний не бесконечно, а много больше, чем их период ($\tau \gg T$). За время жизни происходит много колебательных движений.

Строго говоря, затухающие колебания не являются строго периодическими движениями. Периодом в данном случае считают промежуток времени между двумя последовательными максимальными отклонениями от положения равновесия.

Период затухающих колебаний считают равным:

Пусть $A\left(t\right)\ и\ A(t+T)$ — амплитуды двух последовательных колебаний, моменты времени которых отличаются на период. Отношение этих амплитуд, следуя (10) равно:

называют декрементом затухания. Натуральный логарифм декремента затухания ($\theta $):

называют логарифмическим декрементом затухания. Для колебательной системы $\theta $ постоянная величина.

Примеры задач с решением

Задание. Каков коэффициент затухания маятника ($\gamma $), если за $\Delta t$ амплитуда его колебаний уменьшилась в $n$ раз?

Решение. За основу решения задачи примем уравнение затухающих колебаний в виде:

По условию задачи имеем:

С другой стороны:

где $t_2-t_1=\Delta t$. Найдем натуральный логарифм от правой и левой части выражения (1.2), получим:

Выразим $\gamma $ из (1.3) учтем, что $\frac=n$:

Ответ. $\gamma =\frac<<\ln n\ >><\Delta t>$

Задание. Что представляет собой фазовая траектория затухающего колебания?

Решение. Фазовой траекторией называют траекторию движения в плоскости $\left(x;;v\right).$ По оси абсцисс откладывается отклонение $x$, по оси ординат откладывают скорость $v$. Каждому движению в момент времени $t$ соответствует изображающая точка, на указанной плоскости координаты ее $\left(x,v\right),$ они однозначно определены мгновенными значениями отклонения и скорости. Точка со временем движется и описывает траекторию (рис.1). В данном случае время выступает как параметр, уравнение фазовой траектории задет функция:

Фазовая траектория затухающего колебания, если

\[<\overline>_

=-\beta \overline\left(2.2\right),\]

представляет собой незамкнутую спираль, которая закручивается вокруг начала координат (рис.1). Если затухание колебаний малое, то есть за время жизни колебательная система совершает множество колебаний, количество витков спирали в фазовой плоскости будет таким же.

источники:

http://nsportal.ru/ap/library/nauchno-tekhnicheskoe-tvorchestvo/2019/09/09/izuchenie-zatuhayushchih-kolebaniy

http://www.webmath.ru/poleznoe/fizika_46_zatuhajushhie_kolebanija.php