Методы описания и анализа систем управления. Описание и анализ линейных систем с помощью дифференцианых уравнений.
Читайте также:
|
 |






|





|
g(t) + y(t)
 |

|
y(t)
Рис. 28. Инерционное звено первого порядка
Методика представления САУ в виде структурных схем используется, в частности, при решении задач с помощью аналоговой и цифровой вычислительной техники.
По структурной схеме всегда можно составить дифференциальные уравнения системы.
Анализ выходных процессов может быть проведен по результатам решения дифференциальных уравнений аналитическими методами, численными методами на ЭВМ или интегрированием дифференциальных уравнений по структурным схемам на аналоговой вычислительной технике.
Для линейных систем справедлив принцип суперпозиции: эффект, вызываемый суммой нескольких воздействий, равен сумме эффектов каждого из воздействий в отдельности. Поэтому выходной сигнал линейной САУ при аналитическом решении представляется в виде суммы свободного и вынужденного движений:

Дата добавления: 2015-04-18 ; просмотров: 61 ; Нарушение авторских прав
2. Математическое описание систем автоматического управления
Публикую первую часть второй главы лекций по теории автоматического управления.
В данной статье рассматриваются:
2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
2.2. Линеаризация уравнений динамики САУ (САР)
2.3. Классический способ решения уравнений динамики
Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.
Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.
2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
При составлении уравнений, описывающих нестационарные процессы в САУ (САР) и которые в дальнейшем будем называть уравнениями динамики, система “разбивается” на отдельные элементы (звенья), для каждого из которых не существует проблем в записи соответствующего уравнения динамики.
На рис. 2.1.1 представлено схематичное представление САУ (звена) в переменных «вход-выход», где x(t) (или u(t)) — входное воздействие, а y(t) — выходное воздействие, соответственно. Нередко входное воздействие будет называться управляющим, а выходное воздействие — регулируемой величиной (переменной).
При составлении уравнений динамики используются фундаментальные законы сохранения из разделов “Механики”, “Физики”, “Химии” и др.
Например, при описании перемещения узла какого-то механизма силового привода используются законы сохранения: момента, энергии, импульса и др… В теплофизических (теплогидравлических) системах используются фундаментальные законы сохранения: массы (уравнение неразрывности), импульса (уравнение движения), энергии (уравнение энергии) и др
Уравнения сохранения в общем случае содержат постоянные и нестационарные члены, причем при отбрасывании нестационарных членов получают так называемые уравнения статики, которые соответствуют уравнениям равновесного состояния САУ (звена). Вычитанием из полных уравнений сохранения стационарных уравнений получают нестационарные уравнения САУ в отклонениях (от стационара).
где: — стационарные значения входного и выходного воздействий;
— отклонения от станционара, соотвесвенно.
В качестве примера рассмотрим «технологию» получения уравнений динамики для механического демпфера, схематическое изображение которого представлено на рис. 2.1.2.
Согласно 2-му закону Ньютона, ускорение тела пропорционально сумме сил, действующих на тело:
где, m — масса тела, Fj — все силы воздействующие на тело (поршень демпфера)
Подставляя в уравнение (2.1.1) все силы согласно рис. 2.2, имеем:
где — сила тяжести;
— сила сопротивления пружины,
— сила вязконо трения (пропорциональна скорости поршеня)
Размерности сил и коэффициентов, входящих в уравнение (2.1.2):
Предполагая, что при t ≤ 0 поршень демпфера находился в равновесии, то есть
перейдем к отклонениям от стационарного состояния:
Пусть при t>0 . Тогда, подставляя эти соотношения в уравнение (2.1.2), получаем:
если , то уравнение принимает вид:
Соотношение (2.1.4) – уравнение звена (демпфера) в равновесном (стационарном) состоянии, а соотношение (2.1.5) – статическая характеристика звена – демпфера (см. рисунок 2.1.3).
Вычитая из уравнения (2.1.3) уравнение (2.1.4), получаем уравнение динамики демпфера в отклонениях:
тогда, разделив на k, имеем:
Уравнение (2.1.6) — это уравнение динамики в канонической форме, т.е. коэффициент при Δy(t) равен 1.0!
«Легко» видеть, что коэффициенты перед членами, содержащими производные, имеют смысл (и размерность!) постоянных времени. В самом деле:
Таким образом, получаем, что:
— коэффициент перед первой производной имеет размерность [c] т.е. смысл некоторой постоянной времени;
— коэффициент перед второй производной: [];
— коэффициент в правой части (): [
].
Тогда уравнение (2.1.6) можно записать в операторной форме:
, что эквивалентно
где: — оператор диффренцирования;
-линейный дифференциальный оператор;
— линейный дифференциальный оператор, вырожденный в константу, равную
.
Анализ уравнения (2.1.6.а) показывает, что такое уравнение имеет размерные переменные, а также размерными являются все коэффициенты уравнения. Это не всегда удобно. Кроме того, если реальная САР (САУ) состоит из многих звеньев, выходными воздействиями которых являются различные физические переменные (скорость, температура, нейтронный поток, тепловой поток и т.д.), то значения коэффициентов могут различаться на большое число порядков, что ставит серьезные математические проблемы при численном решении уравнений динамики на компьютере (поскольку числа в компьютере всегда представляются с какой-то точностью). Одним из наилучших способов избежать численных трудностей является принцип нормализации, т.е. переход к безразмерным отклонениям, которые получены нормированием отклонения на стационарное значение соответствующей переменной.
Введем новые нормированные (безразмерные) переменные:
Подставляя эти соотношения в уравнение (2.1.2), имеем:
Поддчеркнутые члены выражения в сумме дают 0 (см. 2.1.4) Перенося в левую часть члены, содержащие , и, разделив на
, получаем:
где: — коэффициент усиления, причем безразмерный.
Проверим размерность коэффициента
Использованный выше «технический» прием позволяет перейти к безразмерным переменным, а также привести вид коэффициентов в уравнении динамики к легко интерпретируемому виду, т.е. к постоянным времени (в соответствующей степени) или к безразмерным коэффициентам усиления.
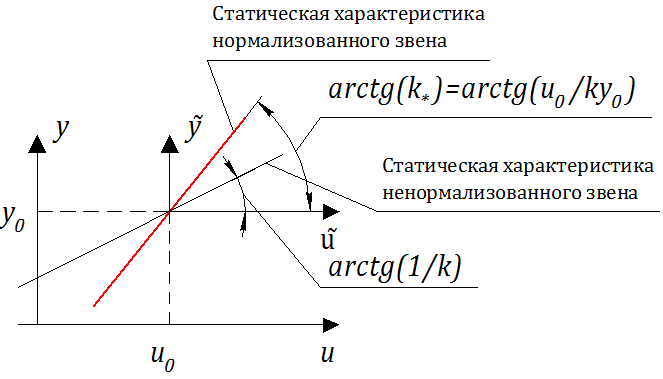
На рис. 2.1.4 представлены статические характеристики для механического демпфера:
Процедура нормировки отклонений позволяет привести уравнения динамики к виду:
где дифференциальные операторы.
Если дифференциальные операторы — линейные, а статическая характеристика САУ (звена) – тоже линейна, то выражение (2.1.8) соответствует линейному обыкновенному дифференциальному уравнению (ОДУ).
А если – нелинейные дифференциальные операторы, или
, то уравнение динамики — нелинейное. Под нелинейными действиями понимаются все математические действия, кроме сложения (+) и вычитания (-).
Пример создания модели демпфера можно посмотереть здесь: «Технология получения уравнений динамики ТАУ»
2.2. Линеаризация уравнений динамики САУ (САР)
Практически все реальные системы автоматического управления (САУ) являются нелинейными, причем нелинейность САУ может определяться различными причинами:
- Нелинейностью статической характеристики.
- Нелинейностью динамических членов в уравнениях динамики.
- Наличием в САУ принципиально нелинейных звеньев.
Если в замкнутой САУ (САР) нет принципиально нелинейных звеньев, то в большинстве случаев уравнения динамики звеньев, входящих в систему, могут быть линеаризованы. Линеаризация основана на том, что в процессе регулирования (т.е. САУ с обратной связью) все регулируемые величины мало отклоняются от их программных значений (иначе система регулирования или управления не выполняла бы своей задачи).
Например, если рассмотреть управление мощностью энергетического ядерного реактора, то главная задача САР — поддержание мощности на заданном (номинальном) уровне мощности. Существующие возмущения (внутренние и внешние) “отрабатываются” САР и поэтому параметры ядерного реактора незначительно отличаются от стационарных. На рис. 2.2.1 представлена временная зависимость мощности ядерного реактора, где нормированные отклонения мощности ΔN /N0 Рис. 2.2.1 – Пример изменения мощности реактора
Рассмотрим некоторое звено (или САР в целом), описание динамики которого можно представить в переменных “вход-выход”:
Предположим, что динамика данного звена описывается обыкновенным дифференциальным уравнением n-го порядка:
Перенесем в левую часть уравнения и запишем уравнение в виде%
где -– функция регулируемой переменной и ее производных, а также управляющего (входного) воздействия и его производных, причем F – обычно нелинейная функция.
Будем считать, что при t ≤ 0 САУ (звено) находилось в равновесии (в стационарном состоянии). Тогда уравнение (2.2.2) вырождается в уравнение статической характеристики:
Разложим левую часть уравнения (2.2.2) в ряд Тейлора в малой окрестности точки равновесного состояния .
Напомним, что разложение в ряд Тейлора трактуется следующим образом: если , то «простое» разложение функции в ряд Тейлора в окрестности точки
будет выглядеть так:
C учетом вышеприведенного разложение принимает вид:
Предполагая, что отклонения выходных и входных воздействий незначительны, (т.е.:), оставим в разложении только члены первого порядка малости (линейные). Поскольку
, получаем:
Подставляя соотношение (2.2.4) в уравнение (2.2.2), и перенося множители при у и u в разные части получаем уравнения:
Коэффициенты — постоянные коэффициенты, поэтому уравнения 2.2.5 — линейное дифференциальное с постоянными коэффициентами.
В дальнейшем нами будет часто использоваться операторная форма записи уравнений динамики:
где – оператор дифференцирования;
— линейный дифференциальный оператор степени n;
— линейный дифференциальный оператор степени m, причем обычно порядок оператора
выше порядка оператора
:
Уравнения (2.2.5) и (2.2.6) — уравнения динамики системы (звена) в отклонениях.
Если исходное уравнение (2.2.1) — дифференциальное уравнение в физических переменных (температура, скорость, поток и т.д.), то размерность коэффициентов может быть произвольной (любой).
Переход к нормализованным отклонениям позволяет “упорядочить” размерность коэффициентов. В самом деле, разделив уравнение (2.2.5) на начальные условия (значения в нулевой момент времени) и выполнив некоторые преобразования, получаем:
Приведение уравнения динамики САУ (звена) к нормализованному виду позволяет “унифицировать” размерность коэффициентов уравнений: ==>
Если вынести в правой части (2.2.7) коэффициент за общую скобку и разделить все уравнение на
, то уравнение принимает вид:
или в операторном виде:
Линеаризация уравнений динамики и нормализация переменных позволяют привести уравнения динамики САУ (звена) к виду, наиболее удобному для использования классических методов анализа, т.е. к нулевым начальным условиям.
Пример
Выполнить линеаризацию уравнения динамики некоторой «абстрактной» САР в окрестности состояния (x0, y0), если полное уравнение динамики имеет вид:
Нелинейность полного уравнения динамики проявляется в следующем:
• во-первых, в нелинейности статической характеристики:
• во-вторых, слагаемое в левой части — чисто нелинейное, так как действие умножения является нелинейным.
Выполним процесс линеаризации исходного уравнения, динамики без разложения я ряд Тейлора, основываясь на том, что в окрестности состояния (x0, y0) нормированные отклонения управляющего воздействия и регулируемой величины намного меньше 1.
Преобразования выполним в следующей последовательности:
- Перейдем к безразмерным переменным (нормализованным);
- Выполним линеаризацию, отбросив нелинейные члены 2-го и выше порядков малости.
Перейдем к новым безразмерным переменным:
Заметим, что: .
Подставляя значения x(t) и y(t) в исходное уравнение:
Удаляем полученного уравнения уравнения стационара: , а так же пренебрегая слагаемыми второго прядка малости:
, получаем следующее уравнение:
Вводим новые обозначения:
Получаем уравнения в «почти» классическом виде:
Если в правой части вынести за общую скобку и разделить все уравнение на
, то уравнение (линеаризованное) принимает вид:
Процедура нормализации позволяет более просто линеаризовать уравнение динамики, так как не требуется выполнять разложение в ряд Тейлора (хотя это и не сложно).
2.3. Классический способ решения уравнений динамики
Классический метод решения уравнений динамики САУ (САР) применим только для линейных или линеаризованных систем.
Рассмотрим некоторую САУ (звено), динамика которой описывается линейным дифференциальным уравнением вида:
Переходя к полной символике, имеем:
Выражение (2.3.2) — обыкновенное дифференциальное уравнение (ОДУ), точнее неоднородное ОДУ, так как правая часть ≠ 0.
Известно входное воздействие x(t), коэффициенты уравнения и начальные условия (т.е. значения переменных и производных при t = 0).
Требуется найти y(t) при известных начальных условиях.
где: — решение однородного дифференциального уравнения
y_<част.>(t) $inline$ — частное решение. $inline$
Будем называть решение однородного дифференциального уравнения , собственным решением, так как его решение не зависит от входного воздействия, а полностью определяется собственными динамическими свойствами САУ (звена).
Вторую составляющую решения (2.3.3) будем называть , вынужденным, так как эта часть решения определяется внешним воздействием
, поэтому САУ (САР или звено) “вынуждена отрабатывать” это воздействие:
Напомним этапы решения:
1) Если имеется уравнение вида , то сначала решаем однородное дифференциальное уравнение:
2) Записываем характеристическое уравнение:
3) Решая уравнение (2.3.5), которое является типичным степенным уравнением, каким-либо способом (в том числе и с помощью стандартных подпрограмм на компьютере) находим корни характеристического уравнения
4) Тогда собственное решение записывается в виде:
если среди нет повторяющихся корней (кратность корней равна 1).
Если уравнение (2.3.5) имеет два совпадающих корня, то собственное решение имеет вид:
Если уравнение (2.3.5) имеет k совпадающих корней (кратность корней равна k), то собственное решение имеет вид:
5) Вынужденную часть решения можно найти различными способами, но наиболее распространены следующие способы:
а) По виду правой части.
б) Методом вариации постоянных.
в) Другие методы…
Если вид правой части дифференциального уравнения – относительно несложная функция времени, то предпочтительным является способ а): подбор решения. .
6) Суммируя полученные составляющие (собственную и вынужденную), имеем:
7) Используя начальные условия (t = 0), находим значения постоянных интегрирования .
Обычно получается система алгебраических уравнений.
Решая систему, находим значения постоянных интегрирования
Пример
Найти аналитическое выражение переходного процесса на выходе звена, если
Решение. Запишем однородное ОДУ:
Характеристическое уравнение имеет вид: ; Решая, имеем:
тогда:
где — неизвестные (пока) постоянные интегрирования.
По виду временной функции в правой части запишем как:
Подставляя в исходное уравнение, имеем:
Суммируя , имеем:
Используя 1-е начальное условие (при t = 0), получаем: , а из 2-го начального условия имеем:
Решая систему уравнений относительно и
, имеем:
Тогда окончательно:
Что бы проверить результ, выполним моделирование процесса в SimInTech, для этого преобразуем исходное уравнение к виду:
Создадим модель SimInTech, содержащую исходное динамическое уравнение и полученное аналитическое решение, и выведем результаты на один график (см. рис. 2.3.1).
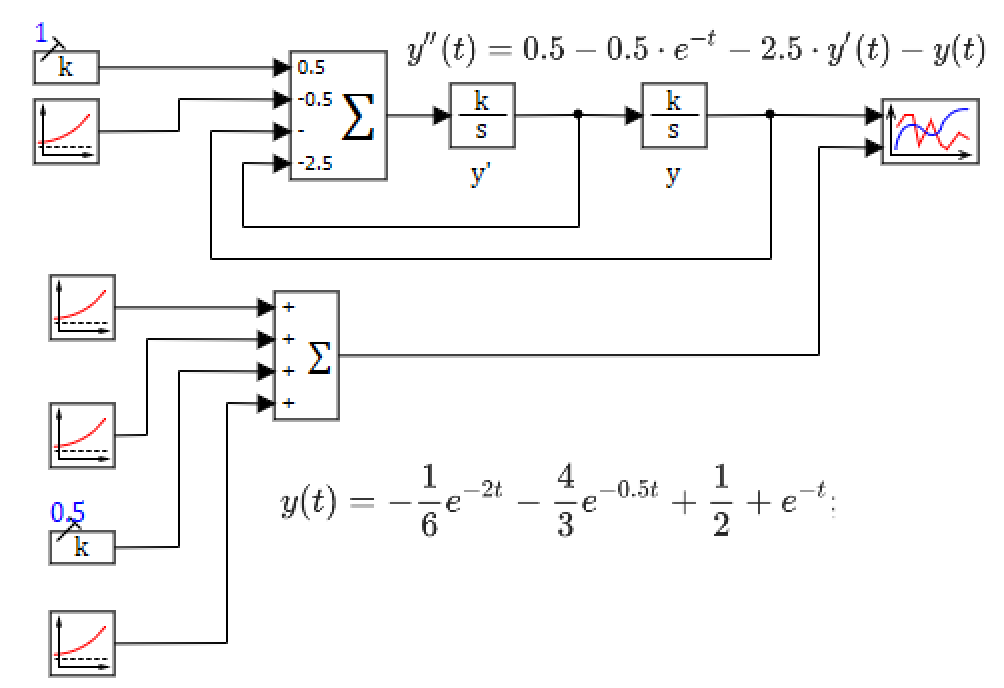
Рис. 2.3.1 – структурная схема для проверки решения
На рис. 2.3.2 приведено решение по вышеприведенному соотношению и численное решение задачи в среде SimInTech (решения совпадают и линии графиков «наложены» друг на друга).
Лекция 3. Математическое описание систем управления
- Борис Докукин 4 лет назад Просмотров:
1 Лекция 3 Математическое описание систем управления В теории управления при анализе и синтезе систем управления имеют дело с их математической моделью Математическая модель САУ представляет собой уравнения передаточные или временные ударение на предпоследнем слоге функции которые описывают процессы протекающие в системе управления Математическая модель может быть получена аналитически на основе физических законов которым подчиняются процессы в системе управления или экспериментально При математическом описании исходят из противоречивых требований С одной стороны математическая модель должна как можно полнее отражать свойства оригинала исходной системы а с другой стороны быть по возможности простой чтобы не усложнять исследование Часто полезно на начальном этапе исследования принимать более простую модель а затем при необходимости усложнять ее принимая во внимание дополнительные факторы которые на начальном этапе не учитывались 3 Уравнения динамики и статики Система управления и любой ее элемент производят преобразование входного сигнала x t в выходной сигнал t С математической точки зрения они осуществляют отображение t Ax t согласно которому каждому элементу x t из множества входных сигналов ставится в соответствие некоторый вполне определенный элемент t из множества выходных сигналов В приведенном соотношении A называется оператором Оператор определяющий отображение между входным и выходным сигналами системы управления элемента называется оператором этой системы элемента Задать оператор системы это значит задать правило определения выходного сигнала этой системы по ее входному сигналу Мы будем рассматривать системы операторы которых могут быть заданы с помощью обыкновенных дифференциальных уравнений Математическая модель системы управления может быть представлена в виде соединения звеньев Звено это математическая модель системы или любой ее части определяемой некоторым оператором В частном случае звено может быть математической моделью элемента Для примера рассмотрим звено которое задается уравнением 3 где у выходная переменная; и входные переменные; точки над переменными обозначают дифференцирование по времени: d d dt dt Пусть при постоянных входных воздействиях и процесс в звене установится: выходная переменная со временем принимает постоянное значение То- гда производные обращаются в нуль и уравнение 3 принимает вид 3 Уравнение 3 описывающее процессы в звене при произвольных входных воздействиях называется уравнением динамики Уравнение 3 описывает статический режим те процесс в звене при постоянных входных воздействиях и называется уравнением статики В общем случае когда звено описывается дифференциальным уравнением значение его выходной величины в момент t зависит от предыстории те от значений входной
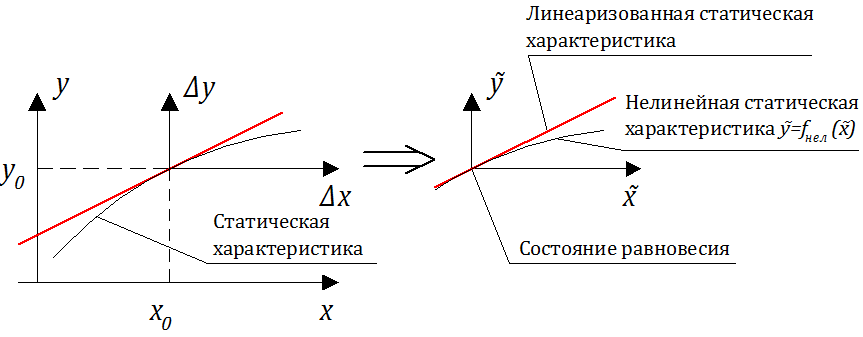
2 переменной до момента t В этом случае говорят что звено обладает динамическим запаздыванием Статический режим можно описать графически с помощью статических характеристик Статической характеристикой звена элемента называют кривую зависимости выходной переменной от входной в статическом режиме Статическую характеристику элемента можно построить экспериментально подавая на вход элемента постоянные воздействия и измеряя значения выходной переменной после окончания переходного процесса или вычисляя с использованием уравнения статики Рассмотрим для примера звено состоящее из подпружиненной массы с демпфером рис 3 а Уравнение динамики для данного звена записываются на основании -го закона Ньютона: k или k Уравнение статики для данного звена имеет вид: а б Рис 3 Статическая характеристика звена представлена на рис 3 б 3 Линеаризация уравнений Большинство систем управления описываются нелинейными дифференциальными уравнениями Но во многих случаях их можно линеаризовать те заменить исходные нелинейные уравнения линейными Процесс преобразования нелинейных уравнений в линейные называют линеаризацией Достаточными признаками возможности проведения линеаризации обычно является отсутствие разрывных неоднозначных или резко изменяющихся характеристик а также правомерность уравнения для всего интервала времени регулирования Назначение систем управления это поддержание некоторого заданного режима При этом режиме входные и выходные переменные звеньев системы изменяются по определенному закону В частности в системах стабилизации они принимают определенные постоянные значения Но из-за различных возмущающих факторов фактический режим отличается от требуемого и текущие значения входных и выходных переменных не равны значениям соответствующим заданному режиму Обычно систему управления проектируют таким образом чтобы реальный процесс мало отличался от требуемого режима те чтобы отклонения от заданного режима были малы Это позволяет производить линеаризацию разлагая нелинейные функции входящие в уравнения в ряд Тейлора в точке соответствующей заданному режиму и отбрасывая нелинейные относительно отклонений и их производных слагаемые Проиллюстрируем сказанное на примере звена заданного уравнением: 33 Пусть заданному режиму соответствуют значения 34 Обозначим отклонения реальных значений и от требуемых через и Тогда получим Подставив эти выражения в исходное уравнение и рассматривая как функцию от независимых переменных и разложим ее в ряд Тейлора в точке 34:
3 3 35 Здесь многоточие обозначает слагаемые содержащие произведения приращений и их производных Пренебрегая этими слагаемыми как бесконечно малыми величинами более высокого порядка чем сами приращения и их производные а также учитывая что в силу 3 последнее уравнение можно представить в виде 36 где Уравнение 36 получено при следующих предположениях: отклонения выходной величины и входных величин и достаточно малы; функция обладает непрерывными частными производными по всем аргументам в окрестности точки соответствующей заданному режиму Если хотя бы одно из этих условий не выполняется то строго говоря линеаризацию проводить нельзя По поводу условия необходимо отметить следующее: нельзя раз и навсегда установить какие отклонения считать малыми; это зависит от вида нелинейности Иногда нелинейную зависимость между отдельными переменными входящими в уравнение звена задают в виде графика кривой В этих случаях линеаризацию можно проводить графически Геометрически линеаризация нелинейной зависимости между двумя переменными означает замену исходной кривой АВ отрезком касательной А’В’ в точке О’ рис 3 соответствующей заданному режиму и параллельный перенос начала системы координат в эту точку 33 Символическая форма записи дифференциальных уравнений При описании систем управления удобно использовать символическую форму записи линейных дифференциальных уравнений Рассмотрим ее на примере уравнения 36 Перепишем его опустив для сокращения записи знак и оставив в левой части только члены содержащие выходную переменную и ее производные: 37 Введем для операции дифференцирования по времени обозначение : i i i dt d dt d Здесь знак тождества обозначает равенство по определению Используя введенное обозначение уравнение 35 можно записать в виде 38 Рассматривая оператор дифференцирования как сомножитель а выражение как произведение не обладающее свойством коммутативности уравнение 38а можно записать в виде 38б Рис 3 Линеаризация
4 Введем обозначения Q R R Используя эти обозначения последнее уравнение можно записать в виде Q R R 38в Следует иметь в виду что уравнения 38а 38в представляют другую символическую операторную форму записи уравнения 37 Иного смысла они не имеют Дифференциальный оператор при выходной переменной называют собственным оператором дифференциальный оператор при входной переменной оператором воздействия В последнем уравнении собственным оператором является Q а операторами воздействия R и R 34 Преобразование Лапласа При рассмотрении линейных дифференциальных уравнений с постоянными коэффициентами удобно использовать преобразование Лапласа так как оно сводит решение дифференциальных уравнений к алгебраическим операциям Преобразованием Лапласа называют соотношение X t x t e dt 4 3 ставящее функции x t вещественного переменного в соответствие функцию X комплексного переменного j При этом x t называют оригиналом X изображением или изображением по Лапласу и переменной преобразования Лапласа Оригинал обозначают строчной а его изображение одноименной прописной буквой Предполагается что функция xt подвергающаяся преобразованию Лапласа обладает следующими свойствами: функция xt определена и кусочно-дифференцируема на интервале [ ; x t при t ; 3 существуют такие положительные числа и M что x t t Me при t Функцию обладающую указанными свойствами называют функцией-оригиналом Соотношение j x t X e t d 3 j j определяющее по известному изображению его оригинал называют обратным преобразованием Лапласа В нем интеграл берется вдоль любой прямой Re Условно прямое и обратное преобразования Лапласа записывают соответственно в виде X x t x t X где оператор Лапласа а обратный оператор Лапласа 34 Основные свойства преобразования Лапласа Свойство линейности Для любых постоянных и x t x t x t x t Дифференцирование оригинала x t X x где X x t x i x t t x Если -я производная t является функцией-оригиналом то
5 k x t k X Здесь x i x t k t x x 5 x x 3 При x x последняя формула принимает вид x t X 3 Интегрирование оригинала Интегрирование оригинала сводится к делению изображения на : t X x d 4 Теорема запаздывания Для любого x t e x t e X 5 Теорема о свертке умножении изображений Если x t и x t оригиналы а X и X их изображения то t t X X x x t d x x t d 33 Интеграл в правой части называют сверткой функций x t и x t его обозначают x t* x t Поэтому X X x t* x t То есть оригинал умножения изображений равен свертке оригиналов 34 Изображения Лапласа распространенных функций Дельта-функция Дельту-функцию t можно определить следующим образом: для любой непрерывной функции t и бесконечно малого положительного числа выполняются следующие равенства: t t t ; t dt ; t t dt t t dt Схематический график дельта-функции показан на рис 33 Изображение Лапласа для дельта-функции: t Единичная функция функция Хевисайда Единичная функция t определяется следующим образом рис 34: t t t Изображение Лапласа для единичной функции: Рис 33 Схематический график дельта-функции Рис 34 График единичной функции
6 X t t t e dt e 3 Единичная функция с запаздывающим аргументом Данная функция определяется следующим образом рис 35: t Рис 35 График t t единичной функции с запаздыванием Согласно теореме запаздывания: X t e t e 4 Функция xt=t При определении изображения функции xt=t используется интегрирование по частям: X t t t t t t e dt t d e e e dt t t 5 Изображение функции x t e Изображение данной функции определяется непосредственно из формулы преобразования Лапласа: X e t t t t t e e dt e dt e 6 35 Передаточные функции Как было показано выше система или звено с одним выходом и двумя входами в общем случае описывается уравнением 34 В символической форме это уравнение принимает вид 35а или Q R R 35б где Q собственный оператор R и R операторы воздействия Наряду с дифференциальными уравнениями при описании линейных систем широко используются передаточные и временные функции Для описания линейных систем используются передаточные функции в операторной форме и передаточные функции в изображениях Лапласа Передаточной функцией в операторной форме называется отношение оператора воздействия к собственному оператору Для системы с одним входом и одним выходом передаточная функция равна: R Q В случае системы управления которая описывается уравнением 34 или 35 имеется два оператора воздействия: оператор воздействия R по входу и оператор воздействия R по входу
7 7 Поэтому в этом случае система определяется двумя передаточными функциями передаточной функцией Q R 36а относительно входа и передаточной функцией Q R 36б относительно входа рис 36 Степень полинома знаменателя называют порядком а разность между степенями знаменателя и числителя относительным порядком передаточной функции и соответствующей системы Нулями и полюсами передаточной функции называют нули ее числителя и знаменателя соответственно те корни уравнений R и Q где рассматривается как переменная а не как оператор С помощью передаточной функции уравнение рассматриваемой системы управления можно записать в виде 37 Передаточная функция в операторной форме является оператором Ее нельзя рассматривать как обычную дробь В частности нельзя числитель и знаменатель сокращать на общий множитель содержащий оператор дифференцирования Пример Определить передаточную функцию в операторной форме для звена описываемого уравнением: Решение В символической форме это уравнение записывается в виде: Передаточная функция равна: Передаточной функцией системы звена в изображениях Лапласа называют имеющее наименьший порядок отношение изображений ее выходной и входной переменных при нулевых начальных условиях Согласно определению передаточная функция в изображениях Лапласа не может иметь равные между собой нули и полюсы так как в этом случае ее порядок можно было бы понизить сократив числитель и знаменатель на общий делитель Если система звено имеет несколько входов то при определении передаточной функции относительно какой-либо одной входной переменной остальные входные переменные полагают равными нулю Найдем передаточные функции в изображениях Лапласа для системы которая описывается уравнением 34 Применим к обеим частям этого уравнения преобразование Лапласа Тогда используя свойство линейности преобразования Лапласа получим Последнее уравнение учитывая свойство преобразования Лапласа дифференцирование оригинала при нулевых начальных условиях можно записать в виде V U Y 38 Рис 36
8 где Y t U t V t Отсюда положив V находим передаточную функцию относительно входа t : Y U 8 Аналогично положив U находим передаточную функцию относительно входа t : Y V Как легко заметить уравнение в изображениях Лапласа 38 получается из дифференциального уравнения 35а те дифференциального уравнения записанного в символической форме при подстановке = и замене переменных их изображениями Поэтому передаточная функция произвольной стационарной линейной системы связана с ее передаточной функцией в операторной форме соотношением 39 В тех случаях когда имеет равные между собой нули и полюсы предполагается что в правой части 39 после подстановки = производится сокращение и передаточная функция не имеет равных между собой нулей и полюсов Обратное соотношение 3 справедливо если передаточная функция не имеет одинаковых нулей и полюсов 36 Временные функции Помимо дифференциальных уравнений и передаточных функций при описании и исследовании линейных систем используют переходные и импульсные переходные функции и их графики временные ударение на предпоследнем слоге характеристики Для линейных систем справедлив принцип суперпозиции который можно сформулировать следующим образом: реакция системы на несколько одновременно действующих воздействий равна сумме реакций на каждое воздействие в отдельности Принцип суперпозиции позволяет сводить исследование систем при нескольких одновременно действующих входных воздействиях к исследованию системы с одним входным воздействием Например пусть требуется найти реакцию системы при двух одновременно действующих входных воздействиях: = t и = t При этом эти воздействия могут быть приложены в одной точке или в разных точках системы Находим сначала реакцию системы t при действии одного входа = t = затем реакцию системы t при действии другого входа = t = Реакция системы при одновременном действии обоих воздействий = t и = t равна сумме найденных реакций: t t t Принцип суперпозиции позволяет во многих случаях ограничиться изучением систем только с одним входом Переходной функцией системы звена называют функцию описывающую реакцию системы на единичное ступенчатое воздействие при нулевых начальных условиях Переходную функцию будем обозначать ht График переходной функции кривую зависимости ht от времени t называют переходной или разгонной характеристикой Импульсной переходной или весовой функцией называют функцию описывающую реакцию системы звена на единичное импульсное воздействие при нулевых начальных условиях
9 Физически единичный импульс можно представить как очень узкий импульс ограничивающий единичную площадь Математически он описывается дельта-функцией t Весовую функцию будем обозначать wt График импульсной переходной функции кривую зависимости функций wt от времени t называют импульсной переходной характеристикой Переходную и импульсную переходную функции называют временными функциями а их графики временными характеристиками 37 Связь между передаточной функцией и временными функциями Между передаточной функцией в изображениях Лапласа переходной функцией и весовой функцией существует взаимнооднозначное соответствие Для установления этого соответствия рассмотрим звено которое описывается уравнением В изображениях Лапласа это уравнение принимает вид: Y U 3 где Y t U t Из определения весовой функции следует что wt при t см рис 37 а И так как при этом Y w t U t то из уравнения 3 получаем а б Рис 37 t w t w t e dt 3 т е передаточная функция в изображениях Лапласа равна изображению Лапласа весовой функции Из определения переходной функции следует что ht при U t / и Y h t то из t см рис 37 б И так как при этом уравнения 3 получаем h t h t Если в последнем уравнении произвести обратное преобразование Лапласа то в силу 3 в левой части получим wt а в правой части в силу свойства преобразования Лапласа связанного с дифференцированием оригинала производную от ht: dh t w t 33 dt При произвольном входном воздействии t из уравнения 3 на основании свойства преобразования Лапласа 33 теорема свертки получаем t t w t d 34 o Итак линейная система звено может быть задана описана с помощью дифференциальных уравнений передаточных функций в операторной форме и в изображениях Лапласа переходной и весовой функциями При этом в общем случае дифференциальные уравнения и передаточные функции в операторной форме описывают систему при произвольных начальных условиях а передаточные функции в изображениях Лапласа и временные переходные и весовые функции только при нулевых начальных условиях 9
10 38 Описание передаточных и временных функций в MATAB В MATAB для описания передаточных функций линейных стационарных систем может быть использовано несколько различных функций Наиболее распространенной является функция tf В MATAB используется объектно-ориентированный подход поэтому результатом выполнения данной функции будет объект который содержит информацию о передаточной функции системы Возможно применение нескольких вариантов использования указанной функции однако здесь рассмотрим самый простой вариант Выражение = tf de возвращает в переменную передаточную функцию системы созданную на основе полинома числителя и полинома знаменателя de При этом переменная содержит вектор-строку в которой записываются коэффициенты полинома числителя начинающие со стоящего при старшей степени а переменная de то же для полинома знаменателя Например для определения в MATAB системы с передаточной функцией: необходимо выполнить следующие команды: = [ 3 4 5]; %коэф-ты полинома числителя de = [ ]; %коэф-ты полинома знаменателя = tf de %передаточная функция Результат выполнения: = ^4 + ^3 + 3 ^ ^5 + 7 ^4 + 8 ^3 + 9 ^ + + Следует отметить что если в полиноме какой-либо из коэффициентов равен нулю то это должно быть явно указано в соответствующем векторе Например передаточная функция: может быть задана следующими командами: = [ 3]; %коэф-ты полинома числителя de = [6 7 8 ]; %коэф-ты полинома знаменателя = tf de %передаточная функция Результат выполнения: = ^ ^3 + 7 ^ + 8 Для исследования САУ во временнóй области используются: функция te позволяющая определить отклик системы на единичное ступенчатое воздействие переходную функцию и функция ie позволяющая определить отклик системы на единичное импульсное воздействие весовую функцию: te; % построение переходной характеристики ie; % построение импульсной переходной хар-ки
http://habr.com/ru/post/506984/
http://docplayer.com/48914194-Lekciya-3-matematicheskoe-opisanie-sistem-upravleniya.html
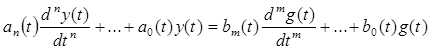 (11.1)
(11.1) (11.2)
(11.2) (11.3)
(11.3) оператор дифференцирования, D(p,t) и M(p,t) — собственный и входной операторы уравнения (11.1).
оператор дифференцирования, D(p,t) и M(p,t) — собственный и входной операторы уравнения (11.1). (11.4)
(11.4)
 при нулевых начальных условиях.
при нулевых начальных условиях.