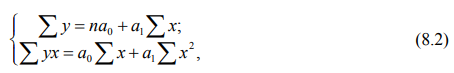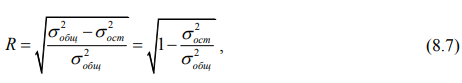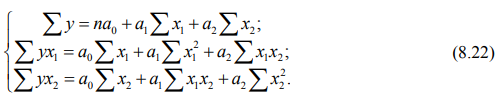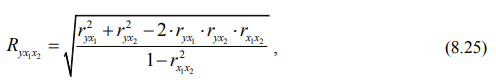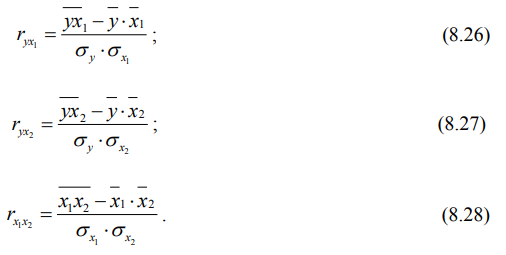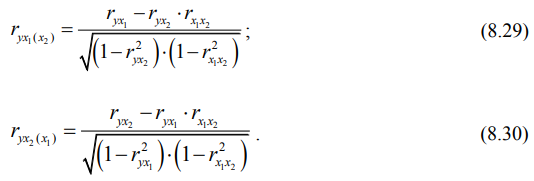Математическое выражение корреляционной зависимости называется уравнением регрессии

Математическое выражение корреляционной зависимости называется уравнением регрессии

В практике сельскохозяйственных и биологических исследований часто возникает необходимость изучить характер связи между двумя (или более) варьирующими признаками или свойствами почв.

Многие признаки и свойства растений находятся между собой в определенной взаимосвязи. Некоторые из них являются взаимосвязанными, другие – изменяются в определенном направлении под влиянием общих условий. Примером связи первого типа может служить зависимость крупности плодов от числа цветков в соцветии, другого – связь между площадью питания растений и урожайностью на разных по плодородию участках.

Что такое переменные? Переменные &#150 это то, что можно измерять, контролировать или что можно изменять в исследованиях. Переменные отличаются многими аспектами, особенно той ролью, которую они играют в исследованиях, шкалой измерения и т.д.

Исследование зависимостей в сравнении с экспериментальными исследованиями. Большинство эмпирических исследований данных можно отнести к одному из названных типов. В исследовании корреляций (зависимостей, связей. ) вы не влияете (или, по крайней мере, пытаетесь не влиять) на переменные, а только измеряете их и хотите найти зависимости (корреляции) между некоторыми измеренными переменными, например, между кровяным давлением и уровнем холестерина. В экспериментальных исследованиях, напротив, вы варьируете некоторые переменные и измеряете воздействия этих изменений на другие переменные. Например, исследователь может искусственно увеличивать кровяное давление, а затем на определенных уровнях давления измерить уровень холестерина. Анализ данных в экспериментальном исследовании также приходит к вычислению &#171корреляций&#187 (зависимостей) между переменными, а именно, между переменными, на которые воздействуют, и переменными, на которые влияет это воздействие. Тем не менее, экспериментальные данные потенциально снабжают нас более качественной информацией. Только экспериментально можно убедительно доказать причинную связь между переменными. Например, если обнаружено, что всякий раз, когда изменяется переменная A, изменяется и переменная B, то можно сделать вывод &#150 &#171переменная A оказывает влияние на переменную B&#187, т.е. между переменными А и В имеется причинная зависимость. Результаты корреляционного исследования могут быть проинтерпретированы в каузальных (причинных) терминах на основе некоторой теории, но сами по себе не могут отчетливо доказать причинность.

Корреляционно-регрессионный анализ применяется для изучения связей и зависимости между наблюдаемыми явлениями. Причинно-следственные связи при математическом анализе могут выражаться в двух формах: функциональной и корреляционной. Под функциональной связью понимают такую связь между какими-либо показателями, когда при изменении одного показателя на определенную величину другой показатель меняется также на строго определенную величину. Функциональные связи характерны для большинства физических, химических и физико-химических явлений. Площадь треугольника точно определяется его высотой и основанием, длина окружности – радиусом, скорость падения является функцией времени падения и ускорения силы тяжести, скорость протекания определенной химической реакции находится в зависимости от температуры.

Необходимо учесть, что в чистом виде функциональные связи встречаются только в идеальных условиях, когда предполагается, что никаких посторонних влияний нет.

Но на практике это недостижимо. Никогда нельзя точно измерить фактически имеющийся радиус круга, причем вычисленная площадь никогда не равна в точности фактической, вследствие практической невозможности начертить точную окружность. Скорость падения реального тела в реальных условиях будет всегда различна при одних и тех же времени и ускорении силы тяжести. На практике всегда действуют посторонние для данной функциональной зависимости факторы, которые нарушают точность этой зависимости в разных случаях по-разному.

Пока такие нарушения остаются настолько незначительными, что их практически можно не учитывать, связь считается функциональной.

При изучении живых объектов приходится иметь дело со связями другого рода. Живой организм развивается в связи с условиями его жизни, под действием бесконечно большого числа факторов, которые по-разному определяют развитие разных признаков. У живых объектов связь между любыми двумя признаками настолько часто и сильно нарушается и модифицируется, что не всегда даже может быть достаточно обнаружена.

Растения, животные, микроорганизмы в процессе своего развития постоянно взаимодействуют с факторами внешней среды, изменяются под влиянием разнообразных условий существования. Поэтому у них связь между признаками проявляется в виде так называемой корреляционной зависимости, или корреляции. Эта форма связи характеризуется тем, что изменение одного показателя на определенную величину сопровождается изменением не одного значения показателя, а целое распределение этих значений при вполне определенных основных показателях этого частного распределения – средней величины и степени разнообразия.

Растения, животные, микроорганизмы в процессе своего развития постоянно взаимодействуют с факторами внешней среды, изменяются под влиянием разнообразных условий существования. Поэтому у них связь между признаками проявляется в виде так называемой корреляционной зависимости, или корреляции. Эта форма связи характеризуется тем, что изменение одного показателя на определенную величину сопровождается изменением другого показателя на различные величины.

Термин корреляция введен в науку Кювье и в переводе с французского означает соотношение, связь (принцип соотношения в каждом организме между различными органами). Таким образом, если при определении значения x переменная y может принимать разные значения с определенной вероятностью, то зависимость между x и y носит характер корреляционной или стохастической связи.

Простейшим визуальным способом выявить наличие взаимосвязи между количественными переменными является построение диаграммы рассеяния (scatterplot). Это график, на котором по горизонтальной оси (X) откладывается одна переменная, по вертикальной (Y) другая. Каждому объекту на диаграмме соответствует точка, координаты которой равняются значениям пары выбранных для анализа переменных.

Направление связи

  1. Если бы существовала функциональная (математически точная) положительная зависимость между числом рабочих и доходом, т.е. если бы на каждом предприятии каждый рабочий за год производил в точности одинаковое количество продукции, все точки-объекты расположились бы на «растущей» прямой.
  2. В этом случае чем больше значения одного признака, тем больше значения другого и чем меньше значения одного признака, тем меньше значения другого.
  3. Пример положительной функциональной связи между признаками X и Y:

Однако на практике мы встречаемся не с функциональными, а со статистическим связями (действительно, эффективность труда, т.е. количество продукции, произведенной одним рабочим, различается на разных предприятиях). Поэтому на графике точки-объекты не лежат на одной прямой, и какую бы прямую мы ни провели, все точки на нее не попадут.

В случае положительной статистической связи мы видим «облако» точек, о котором можно сказать, что оно вытянуто по диагонали от левого нижнего угла к правому верхнему, т.е. с ростом одного признака другой в среднем растет.

Значит, и в этом случае чем больше значения одного признака, тем больше значения другого и чем меньше значения одного признака, тем меньше значения другого. Однако это верно не для каждого объекта, а для статистической совокупности.

Пример положительной статистической связи между признаками X и Y.

Если бы между признаками существовала функциональная отрицательная (а не положительная) зависимость, точки на диаграмме также расположились бы на одной прямой, однако эта прямая проходила бы в противоположном направлении.

В этом случае чем больше значения одного признака, тем меньше значения другого и чем меньше значения одного признака, тем больше значения другого.

Пример отрицательной функциональной связи между признаками X и Y.

Для статистической отрицательной связи мы увидим на графике «облако» точек, о котором можно сказать, что оно вытянуто по диагонали от левого верхнего угла к правому нижнему, т.е. с ростом одного признака другой признак в среднем убывает.

Значит, и в этом случае чем больше значения одного признака, тем меньше значения другого и чем меньше значения одного признака, тем больше значения другого. Однако это верно не для каждого объекта, а для статистической совокупности.

Пример отрицательной статистической связи между X и Y.

Поскольку наиболее простой формой зависимости в математике является прямая, то в корреляционном и регрессионном анализе наиболее популярны линейные модели

Однако иногда расположение точек на диаграмме рассеяния показывает нелинейную зависимость либо вообще отсутствие связи между признаками.

Примеры нелинейной связи (слева) и отсутствия связи (справа) между признаками X и Y

Попробуем провести прямую линию через облако точек на диаграмме рассеяния. Таких линий можно нарисовать множество, причем на глаз невозможно определить, какая из них лучше подходит для описания диаграммы рассеяния.

Однако существует метод, который позволяет совершенно точно вычислить положение прямой линии, наилучшим образом проходящей через облако точек. Это – метод наименьших квадратов.

Вычисляемая с его помощью прямая линия называется линией регрессии. Она характеризуется тем, что сумма квадратов расстояний от точек на диаграмме до этой линии минимальна (по сравнению со всеми возможными линиями).

Таким образом, линия регрессии дает наилучшее приближенное описание линейной зависимости между двумя переменными.

Если объекты характеризуются целым набором количественных признаков, можно построить т.н. матрицу корреляции, т.е. квадратную таблицу, число строк и столбцов которой равно числу признаков, а на пересечении каждых строки и столбца стоит коэффициент корреляции соответствующей пары признаков.

Матрица симметрична, т.е. значения выше и ниже диагонали повторяются (т.к. rxy = ryx).

Пример матрицы корреляции для трех признаков. В этой матрице 9 коэффициентов: по диагонали 3 единицы (корреляция каждого признака с самим собой) и три коэффициента для трех пар признаков: r12, r13 и r23, которые повторяются выше и ниже диагонали:

Некоторые коэффициенты в матрице корреляции показаны красным цветом. Это означает, что они являются статистически значимыми.

В чем смысл понятия статистической значимости применительно к коэффициенту корреляции?

Задача исследования корреляционной связи &#150 определить характер и измерить тесноту сопряженности между признаками, из которых один является факториальным, другой результативным. Например, существует определенная корреляция между числом листьев у кукурузы (факториальный признак) и длиной вегетационного периода (результативный признак): чем больше листьев образует растение, тем позднее оно созревает.

Прежде чем приступать к рассмотрению сущности корреляционно — регрессионного анализа, необходимо выделить условия его применения и ограничения:

1) Корреляционную связь не следует вычислять при значении коэффициента корреляции более 30% в каждом из рядов наблюдений.

2) Число наблюдений должно быть не менее чем в 5-6 раз больше числа факторов.

3) Необходимо, чтобы совокупности по результативному и факториальному признакам подчинялись нормальному закону распределения вероятностей.

Исследование корреляции сводится к следующему:

1. Устанавливают факт зависимости изменений одного признака от изменения другого и определяют форму связи между ними (тип корреляции). Корреляцию называют простой, если исследуется связь между двумя признаками, или множественной, когда на величину одного результативного признака влияют несколько факториальных.

2. В зависимости от характера изменений результативного признака под влиянием факториального различают следующие формы корреляции:

а) линейную корреляцию, когда с увеличением среднего значения одного признак также увеличивается среднее значение другого, или с увеличением среднего значения одного признака уменьшается среднее значение другого. В первом случае корреляцию называют прямой, во втором – обратной;

б) криволинейную корреляцию: при возрастании значения одного признака другой принимает значения, возрастающие до определенной величины, а затем убывающие, или наоборот.

3.Находят тесноту связи, т.е. степень сопряженности между значениями одного и другого признака. Основной показатель степени сопряженности между значениями одного и другого признака и формы связи — коэффициент корреляции (r). Коэффициент корреляции – безразмерная величина, изменяемая в пределах -1&#8805 r &#8804 +1. При r = 0 линейная связь отсутствует, при r = &#177 1 корреляционная связь превращается в функциональную.

Определение тесноты связи по величине коэффициента корреляции следующее:

r = 0,3 – 0,7 – средней;

r &#8805 0,7 – сильной связи.

Статистическая значимость коэффициента корреляции

Если коэффициент корреляции вычислен на основе выборочных данных, то не исключено, что его ненулевое значение является не отражением действительной связи между признаками, а просто получено в результате специфики данной выборки (тогда как в генеральной совокупности коэффициент корреляции равен нулю, т.е. линейной связи между признаками нет).

Таким образом, надо понять, как далеко значение r от нуля.

Если значение коэффициента корреляции вычислено по выборочным данным, то для оценки его значения в генеральной совокупности, как обычно, строится доверительный интервал.

Для построения доверительного интервала вычисляется ошибка коэффициента корреляции &#963r по формуле:

Затем ошибка коэффициента корреляции умножается на параметр t, зависящий от доверительной вероятности P (для вероятности 95% t = 2), чтобы найти предельную ошибку.

Наконец, строится доверительный интервал r &#177 &#963r и проводится проверка, попадет ли нулевое значение в этот интервал.

Если ноль не попадет в доверительный интервал, значит с высокой вероятностью в генеральной совокупности не может быть нулевого значения коэффициента корреляции, т.е. связь между признаками существует и в генеральной совокупности. В таком случае коэффициент корреляции является статистически значимым

Если две переменные линейно независимы (метод наименьших квадратов дает горизонтальную прямую), то одна из них в своих изменениях никоим образом не определяет другую – в этом случае коэффициент детерминации равен нулю.

В остальных случаях коэффициент детерминации указывает, какая часть изменений одной переменной объясняется изменениями другой переменной.

Чем выше по модулю (по абсолютной величине) значение коэффициента корреляции, тем сильнее связь между признаками.

Принято считать, что коэффициенты корреляции, которые по модулю больше 0,7, говорят о сильной связи (при этом коэффициенты детерминации > 50%, т.е. один признак определяет другой более, чем наполовину).

Коэффициенты корреляции, которые по модулю меньше 0,7, но больше 0,5, говорят о связи средней силы (при этом коэффициенты детерминации меньше 50%, но больше 25%).

Наконец, коэффициенты корреляции, которые по модулю меньше 0,5, говорят о слабой связи (при этом коэффициенты детерминации меньше 25%).

Необходимо подчеркнуть, что величина коэффициента корреляции еще не гарантирует его значимости: даже большой коэффициент может оказаться статистически незначимым (например, при малом объеме выборки), а небольшой коэффициент (если выборка велика) — значимым.

Следует также предостеречь от излишнего злоупотребления математическим описанием анализируемых зависимостей, если природа связи неизвестна и теоретически оправданных предположений о виде уравнения нет. Конечно, процесс отбора может завершиться нахождением уравнения, которое неплохо описывает изучаемое явление. Но не следует забывать, что не имеющее физического смысла уравнение может затушевать весьма важные особенности явления или процесса.

Именно поэтому проведенная от руки линия регрессии или найденная путем сглаживания с помощью скользящей средней нередко оказывается гораздо более полезной, чем с большим трудом подобранное математическое описание. Следует помнить, что математическое выражение лишь тогда полезно, когда оно позволяет дополнительно вскрыть какие-то особенности процесса или помогает прогнозировать процесс, протекающий в аналогичных условиях.

Направление корреляционной зависимости определяется знаком: положительное значение свидетельствует о том, что изменения одной величины соответствуют изменениям другой, т.е с увеличением значения одной увеличивается другая, а связь — прямая. При отрицательной корреляции (обратная зависимость), наоборот, с увеличением значения одной величины другая уменьшается, а с уменьшением – увеличивается.

Коэффициент корреляции определяется по формуле:

r = &#8730 (x – x)&#215 (y –y) / &#8730 &#931 (x –x) 2 &#215 &#931 (y – y) 2

Следует иметь в виду, что коэффициент корреляции выборочного наблюдения подвержен случайным колебаниям, зависящим как от особенностей образования выборки, так и от точности наблюдений. Вследствие этого по величине коэффициента корреляции не всегда можно с достаточной уверенностью судить о наличии или сопряженности между признаками в данной выборке. Поэтому вычисленный для выборки коэффициент корреляции необходимо оценить с точки зрения его значимости и убедиться, что его знак не изменится на обратный. Для оценки существенности коэффициента корреляции вычисляют его ошибку (Sr) и критерий существенности (tr)по формулам:

Sr = &#8730 1 – r 2 / n -2

r – коэффициент корреляции;

n – число парных значений показателей по которым вычислен коэффициент корреляции.

Если tr &#8805 tтеор, то корреляционная связь существенна. Теоретическое значение критерия Стьюдента берут из таблицы при уровнях вероятности 95 и 99% и числе степеней свободы Y = n – 2.

Величина коэффициента корреляции позволяет выяснить тесноту (силу) и направление связи, однако этим не исчерпываются возможности изучения сопряженности между признаками. Более того, во многих исследованиях возникает необходимость изучить не столько меру корреляции, сколько ее форму и характер изменения одного признака в зависимости от изменения другого, т.е. количественное изменение связанных друг с другом показателей или признаков. Последнее особенно важно в тех случаях, когда фактические наблюдения не охватывают всего разнообразия признака и цель исследования заключается в том, чтобы выяснить взаимозависимости между недостающими данными. Эти задачи решаются методами регрессионного анализа.

Термин регрессия был введен Гальтоном в связи с изучением им наследования признаков родителей потомством.

2. Схема корреляционно-регрессионного анализа

Регрессией называется изменение функции при определенных изменениях одного или нескольких аргументов. Функцией называется признак, зависящий от другого – аргумента. Зависимость функции от аргумента может быть или физиологической или условно принятой в исследовании. Примером физиологической зависимости может служить зависимость веса животного (функции) от его возраста (аргумента).

Термин «функция&#187 употребляется не только для обозначения признака, который зависит от аргумента, но и для обозначения формы этой зависимости. Вскрыть функцию – значит найти закономерность, по которой изменяется изучаемый признак в зависимости от изменения одного или нескольких других признаков.

Третьим основным показателем корреляционной связи является коэффициент регрессии – byx, показывающий, в каком направлении и на какую величину в среднем изменяется функция (y) при изменении аргумента (x) на единицу измерения. Кроме того коэффициент регрессии необходим для вычисления теоретических значений результативного признака для любых значений факториального. Коэффициент регрессии измеряется в тех же единицах, что и функция, и имеет тот же знак, что и его коэффициент корреляции. Вычисляется коэффициент регрессии по формуле:

byx = &#931 (x – xср)&#215 (y – yср) / &#931 (x – xср) 2 .

Числитель этой формулы представляет собой сумму произведений отклонений значений x и y от своих средних значений, а знаменатель – сумму квадратов отклонений от средних значений.

При регрессионном анализе производят обычно две оценки выборочных коэффициентов регрессии:

а) оценку существенности коэффициента регрессии;

б) критерий существенности регрессии.

Оценка существенности коэффициента регрессии позволяет убедиться в том, что зависимость между сопоставляемыми признаками не случайна, а статистически значима. Для этого рассчитывают ошибку коэффициента регрессии:

Sbyx= Sr &#8730 &#931 (x –xср) 2 / &#931 (y – yср) 2

Критерий существенности для коэффициента регрессии:

tb= b/ Sb.

При этом следует помнить, что tb = tr и byx*byx = r 2 . Это может служить для проверки правильности расчетов.

В ряде случаев исследователю важно не только установить наличие связи между изучаемыми показателями, но и выразить эту связь в виде математического уравнения. Это требуется в случаях, когда необходимо вычислить неизвестную величину по известным значениям. Например, зная запас минеральных элементов в почве, вычислить урожай культуры. Уравнение, связывающее величины x и y, носит название уравнения регрессии.

Регрессионный анализ заключается в том, чтобы отыскать линию (прямую – в случае линейной корреляции, параболу первого, второго и т.д. порядка при криволинейной зависимости), наиболее точно выражающую зависимость одного признака от другого. Кроме того, при помощи регрессионного анализа можно выяснить ошибку опытных данных, влияющих на конечные результаты исследования.

Наглядным способом выражения корреляционной зависимости служит построение специальных графиков. Поэтому после установления существенности коэффициента регрессии составляют уравнение регрессии, т.е. математическую формулу для данной корреляционной связи. В природе существует множество явлений, обусловленных множеством причин. Поэтому существует много форм зависимости функций от различных аргументов. Исследование этих форм, выраженных математическими уравнениями, составляет основное содержание учения о регрессии признаков. Вскрывая усредненное течение функции, исследователь выявляет ту закономерность изучаемого явления, которая в эмпирическом ряду была скрыта случайностями своего проявления. Эта вскрытая закономерность, выраженная формулой или теоретическим рядом регрессии, помогает более точно, с меньшими ошибками дать описание внешних проявлений закономерности, что, в свою очередь, может помочь вскрытию и внутренних факторов, управляющих данным явлением. В этом и заключается познавательное значение исследование регрессии различных признаков у биологических объектов. Каждый выровненный ряд дает возможность определить значение функции при любом значении аргумента (или нескольких аргументов). Это обстоятельство дает возможность использовать ряды и уравнения регрессии при определении значений таких признаков, непосредственное измерение которых в обычных условиях или невозможно или затруднительно. В простой линейной корреляции уравнение имеет вид:

Регрессионный анализ заключается в том, чтобы отыскать линию (прямую – в случае линейной корреляции, параболу первого, второго и т.д. порядка при криволинейной зависимости), наиболее точно выражающую зависимость одного признака от другого. Кроме того, при помощи регрессионного анализа можно выяснить ошибку опытных данных, влияющих на конечные результаты исследования.

Наглядным способом выражения корреляционной зависимости служит построение специальных графиков. Поэтому после установления существенности коэффициента регрессии составляют уравнение регрессии, т.е. математическую формулу для данной корреляционной связи. В простой линейной корреляции уравнение имеет вид:

y0 = y + byx (x –xср), где

y0 – теоретическое значение признака;

y– средняя арифметическая признака;

x – средняя арифметическая признака;

byx — коэффициент регрессии.

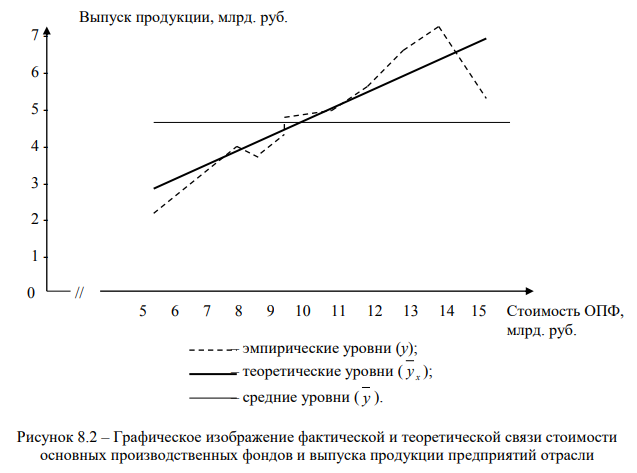
С помощью уравнения регрессии корреляционная связь изображается графически в системе координат в виде линии регрессии.

Для построения теоретической линии регрессии в формулу уравнения подставляют значения y, x, byx. После этого берут два экстремальных значения x (xmin; xmax) и вычисляют соответствующие им значения y. Строят систему координат в масштабе значений, соответствующих изменениям значений y и x. В этой системе находят две экстремальные точки (xmin ; ymin) (xmax ; ymax), по которым и строят линию регрессии.

После построения линии регрессии в этой же системе координат наносят в виде точек фактические экспериментальные значения y и x. Если разброс точек осуществляется вокруг теоретической линии, значит, расчет сделан, верно, и построенный график может быть использован для научных и практических целей.

3. Множественная корреляция

В практике сельскохозяйственного экспериментирования встречаются задачи, когда исследуемая зависимость между двумя признаками определяется влиянием третьего признака. Например, продуктивность колоса характеризуют длина колоса, число семян в колосе и их величина. Все эти признаки варьируют под влиянием условий произрастания, однако число зерен находится в прямой зависимости с размером (длиной) колоса, а крупность – в обратной связи с количеством семян в колосе. Практический интерес представляет коррелятивная связь между длиной колоса и крупностью семян в колосе.

Для того, чтобы выяснить в таких исследованиях, влияет или не влияет третий признак на корреляционную связь между первым и вторым признаком, необходимо исследовать эту связь при постоянных значениях третьего признака. Постоянное значение признака означает, что с чисто внешней стороны невозможно подметить статистического влияния этого признака на все остальные. При постоянном значении признака возможно только констатировать, что в изменчивости других признаков нет его влияния: он постоянен, а другие признаки изменяются. Поэтому, коэффициент корреляции между первым и вторым признаком при постоянном значении третьего считают коэффициентом корреляции между двумя признаками при исключительном влиянии третьего. Такой показатель носит название частного коэффициента корреляции.

В этом случае для определения формы и тесноты связи нескольких факторов рассчитывают коэффициенты частной и множественной корреляции. При множественной линейной корреляции на величину функции одновременно влияют несколько переменных величин.

Частные коэффициенты корреляции для трех факторов определяют форму и тесноту связи между двумя из них при постоянном значении третьего. Вычисляют их по формулам:

Для определения существенности частных коэффициентов корреляции определяют их ошибки и критерии существенности:

Множественные коэффициенты корреляции являются показателями формы и тесноты связи одного фактора с совокупностью других. Множественный коэффициент корреляции может изменяться в пределах от 0 до 1.

Значимость множественного коэффициента корреляции определяется с помощью критерия Фишера по формуле:

F = R 2 / 1 – R 2 &#215 (n – k / k – 1), где

n — объем выборки;

k – число изучаемых факторов;

F0,5 и F0,1 определяются из данных таблиц при Y = k – 1 и Y = n – k.

Если Fфакт &#8805 Fтеор, связь существенна.

4. Криволинейная корреляция

При криволинейном типе связи с увеличением одного фактора другой коррелирующий с ним сначала увеличивается, а затем уменьшается или наоборот. В связи с этим коэффициент корреляции не дает правильного представления о степени связи между признаками. Тогда вычисляют показатель криволинейной зависимости, так называемое корреляционное отношение &#951(эта), представляющее собой отношение двух дисперсий: дисперсия групповых средних и общей дисперсии. Иначе говоря, корреляционное отношение отвечает на вопрос: какую часть общей дисперсии результативного признака составляет дисперсия частных средних этого признака.

Корреляционное отношение не показывает направление связи так как оно всегда имеет положительный знак и принимает значения от нуля до единицы. При &#951 = 1 корреляционная связь превращается в функциональную, при &#951 = 0 связь отсутствует. Корреляционное отношение может применяться для вычисления независимого фактора, хорошо коррелирующего с зависимым фактором.

Корреляционное отношение вычисляется по формулам:

&#951 xy=&#8730 &#931 (y – yср) 2 – (y –yx) 2 /&#931 (y – yср) 2 – для малых выборок

&#951 xy = &#8730 &#931 &#402(yx – yср) 2 / &#931 &#951 (y – yср) 2 – для больших выборок

Существенность корреляционного отношения определяют с помощью его ошибки и критерия существенности:

S&#951 = &#8730 1 – &#951 2 / n -2; t&#951 = &#951 / S&#951

Свойства корреляционного отношения

Основным свойством корреляционного отношения является способность измерять корреляцию при любой ее форме.

Кроме того, корреляционное отношение обладает рядом других свойств, представляющих большой интерес в статистическом анализе корреляционных связей.

В отличие от коэффициента корреляции, который дает одинаковую меру связи признаков первого со вторым и второго с первым, корреляционное отношение второго признака по первому обычно не бывает равно корреляционному отношению первого признака по второму:

На первый взгляд это кажется невозможным. Казалось бы, между двумя признаками может только одна связь, которая в данный момент всегда равна самой себе независимо от того с какого признака мы начинаем ее измерять: от второго к первому или наоборот.

На самом деле это положение не всегда подтверждается практикой измерения обратных связей в биологии и сельском хозяйстве.

Конечно, если изучается связь между такими парами признаков, как длина и ширина тела, цвет волос и цвет глаз, вес и объем продукта, урожайность на соседних делянках, равенство обратных связей не подлежит сомнению.

Однако существуют такие пары коррелируемых признаков, для которых очевидно, что обратные связи не могут быть равны. Например, связь с возрастом различных признаков животных и растений всегда имеет характер односторонней изменчивости. Вес, размеры, объем, продуктивность, плодовитость, жизненность имеют явную зависимость от возраста, при этом сам возраст изменяется совершенно независимо от этих признаков: он регулярно и неотвратимо увеличивается с каждым днем, месяцем, годом. Связь урожая с количеством осадков или с температурой также имеет характер явно односторонней зависимости: урожай связан с температурой воздуха, но температура воздуха не как не зависит от урожая.

Это неравенство обратных связей между условиями жизни и жизненными функциями и отражается в неравенстве двух обратных корреляционных отношений.

5. Корреляционно-регрессионные модели и их применение в анализе и прогнозе

Корреляционно-регрессионной моделью системы взаимосвязанных признаков является такое уравнение регрессии, которое включает основные факторы, влияющие на вариацию результативного признака, обладает высоким (не ниже 0,5) коэффициентами детерминации и коэффициентами регрессии, интерпретируемыми в соответствии с теоретическим знанием о природе связей в изучаемой системе. Параметры уравнения оцениваются методом наименьших квадратов. Уравнение регрессии должно быть линейным по параметрам.

Если уравнение регрессии отражает нелинейность связи между переменными, то регрессия приводится к линейному виду путем замены переменных или их логарифмирования.

Если коэффициент детерминации близок к единице, то с помощью уравнения регрессии можно предсказать, каким будет значение зависимой переменной для того или иного ожидаемого значения одной или нескольких независимых переменных.

Приведенное определение корреляционно-регрессионной модели включает достаточно строгие условия: далеко не всякое уравнение регрессии можно считать моделью.

Теория и практика выработали ряд рекомендаций для построения корреляционно-регрессионной модели.

1. Признаки – факторы должны находиться в причинной связи с результативным признаком (следствием).

2. Признаки — факторы не должны быть составными частями результативного признака или его функциями.

3. Признаки – факторы не должны дублировать друг друга, т.е. быть коллинеарными (с коэффициентом корреляции более 0,8).

4. Не следует включать в модель факторы разных уровней иерархии, т.е. фактор ближайшего порядка и его субфакторы.

5. Важно, чтобы для результативного признака и факторов соблюдалось единство единицы совокупности, к которой они отнесены.

6. Математическая форма уравнения регрессии должна соответствовать логике связи факторов с результатом в реальном объекте.

7. Принцип простоты: предпочтительнее модель с меньшим числом факторов при том же коэффициенте детерминации или даже при несущественно меньшем.

Контрольные вопросы

  1. Что такое функциональная и корреляционная связь, в чем их различие?
  2. С помощью каких показателей оценивается корреляционная связь?
  3. Что такое коэффициент простой линейной корреляции, какие значения он может принимать?
  4. В чем суть и значение коэффициента регрессии?
  5. Что такое доверительная зона регрессии?
  6. В чем смысл коэффициента детерминации?

НазадНаверхДалее

© ФГОУ ВПО Красноярский государственный аграрный университет

РЕГРЕССИОННЫЙ АНАЛИЗ

В практических исследованиях возникает необходимость аппроксимировать (описать приблизительно) диаграмму рассеяния математическим уравнением . То есть зависимость между переменными величинами Y и Х можно выразить аналитически с помощью формул и уравнений и графически в виде геометрического места точек в системе прямоугольных координат. График корреляционной зависимости строится по уравнениям функции и , которые называются регрессией (термин “регрессия” происходит от лат. regressio — движение назад). Здесь и — средние арифметические из числовых значений зависимых переменных Y и X .
Для выражения регрессии служат эмпирические и теоретические ряды, их графики — линии регрессии , а также корреляционные уравнения (уравнения регрессии) и коэффициент линейной регрессии.
Показатели регрессии выражают корреляционную связь двусторонне, учитывая изменение средней величины признака Y при изменении значений x i признака X , и, наоборот, показывают изменение средней величины признака Х по измененным значениям y i признака Y . Исключение составляют временные ряды, или ряды динамики, показывающие изменение признаков во времени. Регрессия таких рядов является односторонней.
Ряды регрессии , особенно их графики, дают наглядное представление о форме и тесноте корреляционной связи между признаками, в чем и заключается их ценность. Форма связи между показателями, влияющими на уровень спортивного результата и общей физической подготовки занимающихся физической культурой и спортом, может быть разнообразной. И поэтому задача состоит в том, чтобы любую форму корреляционной связи выразить уравнением определенной функции (линейной, параболической и т.д.), что позволяет получать нужную информацию о корреляции между переменными величинами Y и X , предвидеть возможные изменения признака Y на основе известных изменений X , связанного с Y корреляционно.

Линии регрессии, как показано, пересекаются в точке 0 ( ), соответствующей средним арифметическим значениям корреляционно связанных друг с другом признаков Y и X . Линия АВ, проходящая через эту точку, изображает полную (функциональную) зависимость между переменными вели-чинами Y и X , когда коэффициент корреляции r = 1 . Чем сильнее связь между Y и X , тем ближе линии регрессии к АВ, и, наоборот, чем слабее связь между варьирующими признаками, тем более удаленными оказываются линии регрессии от АВ. При отсутствии связи между признаками, когда r = 0 , линии регрессии оказываются под прямым углом (90°) по отношению друг к другу.
Уравнение регрессии тем лучше описывает зависимость, чем меньше рассеяние диаграммы, чем больше теснота взаимосвязи. Уравнение прямой линии пригодно для описания только линейных зависимостей. В случае не-линейных зависимостей математическая запись может отображаться уравнениями параболы, гиперболы и др.
Необходимо также сделать одно важное замечание о значении показателей, характеризующих взаимосвязь признаков (коэффициентов корреляции, регрессии и т. п.). Все они дают лишь количественную меру связи, но ничего не говорят о причинах зависимости. Определить эти причины — дело самого исследователя.

Значение этой оценки, если r = , равно нулю и, если r = 0 , максимально. Остаточное среднее квадратическое отклонение характеризует колеблемость Y относительно линии регрессии по Х в прямом уравнении регрессии и, наоборот, в обратном случае. А, следовательно, чем меньше вели-чина относительной погрешности уравнения регрессии, тем точнее будет оно осуществлять прогноз значений одного показателя по заранее известным значениям другого.

Эта формула ценна тем, что, во-первых, может быть использована для нахождения неизвестной величины коэффициента корреляции по известным значениям коэффициента регрессии b y/x и b x/y , а во-вторых, позволяет контролировать правильность расчета коэффициента корреляции, если известны величины b y/x и b x/y . Знак выборочного коэффициента корреляции совпадает со знаком выборочных коэффициентов регрессии, что следует из формулы (2.3). Если зависимость между признаками функциональная, то b y/x = 1 / b x/y и, следовательно, r = 1 . И, наоборот, при полном отсутствии взаимосвязи между признаками b y/x = 0, b x/y = 0 , и r = 0 .

Эти уравнения удобны для определения параметров при отыскивании эмпирических уравнений регрессии в практической работе для точности прогнозирования результатов.

Методические основы корреляционно-регрессионного анализа

Понятие о корреляционно-регрессионном анализе

Убедившись при помощи аналитической группировки и расчета показателя эмпирического корреляционного отношения, что теснота связи между исследуемыми явлениями достаточно высока, можно и перейти к корреляционно-регрессионному анализу.

Экономические явления и процессы хозяйственной деятельности предприятий зависят от большого количества взаимодействующих и взаимообусловленных факторов.

В наиболее общем виде задача изучения взаимосвязей факторов состоит в количественной оценке их наличия и направления, а также характеристике силы и формы влияния одних факторов на другие. Для ее решения применяются две группы методов, одна из которых включает в себя методы корреляционного анализа, а другая – методы регрессионного анализа, объединенные в методы корреляционно-регрессионного анализа, что имеет под собой некоторые основания: наличие целого ряда общих вычислительных процедур, взаимодополнение при интерпретации результатов и др.

Задачи корреляционного анализа сводятся к измерению тесноты связи между варьирующими признаками и оценке факторов, оказывающих наибольшее влияние на результативный признак. К показателям, используемым для оценки тесноты связи, относятся эмпирическое корреляционное отношения, теоретическое корреляционное отношение, линейный коэффициент корреляции и т.п.

Задачи регрессионного анализа состоят в установлении формы зависимости между исследуемыми признаками (показателями), определении функции регрессии, использования уравнения регрессии для оценки неизвестных значений зависимой переменной. Найти уравнение регрессии –

значит по эмпирическим (фактическим) данным описать изменения взаимно коррелируемых величин.

Уравнение регрессии должно определить, каким будет среднее значение результативного признака у при том или ином значении факторного признака х, если остальные факторы, влияющие на у и не связанные с х не учитывать, т.е. абстрагироваться от них. Уравнение регрессии называют теоретической линией регрессии, а рассчитанные по нему значения результативного признака – теоретическими. Теоретические значения результативного признака обычно обозначаются y x (читается: «игрек, выровненный по икс») и рассматриваются как функция от х, т.е. y x = f (x). Иногда для простоты записи вместо y x пишут y’ или y.

Для аналитической связи между х и у используются следующие простые виды уравнений: y x = a0 + a1x (прямая); y x = a0 + a1x + a2x 2 (парабола второго порядка); y x = a0 + a1/x (гипербола); y x = a0 × a1 x (показательная или экспоненциальная функция); y x = a0 + b × lg x (логарифмическая функция) и др.

Обычно зависимость, выраженную уравнением прямой, называют линейной (или прямолинейной), а все остальные – криволинейными (см. табл. 7.1). Кроме того, различают парную и множественную (многофакторную) корреляцию (см. там же), а, следовательно, и, парную и множественную регрессии.

Корреляционно-регрессионный анализ, в частности многофакторный корреляционный анализ, состоит из нескольких этапов.

На первом этапе определяются факторы, оказывающие воздействие на изучаемый показатель, и отбираются наиболее существенные. От того, насколько правильно сделан отбор факторов, зависит точность выводов по итогам анализа. При отборе факторов придерживаются требований, представленных на рис. 8.1.

Требования к отбору факторов при корреляционнорегрессионном анализе:

  • учитываются причинно-следственные связи между показателями
  • отбираются самые значимые факторы, оказывающие решающее воздействие на результативный показатель (факторы, которые имеют критерий надежности по Стьюденту меньше табличного, не рекомендуется принимать в расчет)
  • все факторы должны быть количественно измеримы
  • не рекомендуется включать в корреляционную модель взаимосвязанные факторы (если парный коэффициент корреляции между двумя факторами больше 0,85, то по правилам корреляционного анализа один из них необходимо исключить, иначе это приведет к искажению результатов анализа)
  • нельзя включать в корреляционную модель факторы, связь которых с результативным показателем носит функциональный характер
  • в корреляционную модель линейного типа не рекомендуется включать факторы, связь которых с результативным показателем имеет криволинейный характер

Рисунок 8.1 – Перечень основных требований, учитываемых при отборе факторов, при корреляционно-регрессионном анализе

На втором этапе собирается и оценивается исходная информация, необходимая для корреляционного анализа. Собранная исходная информация должна быть проверена на точность (достоверность), однородность и соответствие закону нормального распределения. Критерием однородности информации служит среднеквадратическое отклонение и коэффициент вариации. Если вариация выше 33%, то это говорит о неоднородности информации и ее необходимо исключить или отбросить нетипичные наблюдения.

На третьем этапе изучается характер и моделируется связь между факторами и результативным показателем, т.е. подбирается и обосновывается математическое уравнение, которое наиболее точно выражает сущность исследуемой зависимости. Для обоснования функции используются те же приемы, что и для установления наличия связи: аналитические группировки, линейные графики и др. Если связь всех факторных показателей с результативным носит прямолинейный характер, то для записи этих зависимостей можно использовать линейную функцию: y x = a0 + a1x1 + a2x2 +. + anxn. Если связь между функцией и исследуемыми показателями носит криволинейный характер, то может быть использована степенная функция: y x = b0 × x1 b1 × x2 b2 × . × xn bn .

На четвертом этапе проводится расчет основных показателей связи корреляционного анализа. Рассчитываются матрицы парных и частных коэффициентов корреляции уравнения множественной регрессии, а также показатели, с помощью которых оценивается надежность коэффициентов корреляции и уравнения связи: критерий Стьюдента, критерий Фишера, множественные коэффициенты корреляции и др.

На пятом этапе дается статистическая оценка результатов корреляционного анализа и практическое их применение. Для этого дается оценка коэффициентов регрессии, коэффициентов эластичности и бета-коэффициентов.

Одним из основных условий применения и ограничения корреляционно-регрессионного метода является наличие данных по достаточно большой совокупности явлений. Обычно считают, что число наблюдений должно быть не менее чем в 5-6, а лучше – не менее чем в 10 раз больше числа факторов.

Парная линейная регрессия

Парная линейная зависимость – наиболее часто используемая форма связи между двумя коррелируемыми признаками, выражаемая при парной корреляции уравнением прямой:

где y x – выровненное среднее значение результативного признака;
х – значение факторного признака;
а0 и а1 – параметры уравнения;
а0 – значение у при х = 0;
а1 – коэффициент регрессии.

Коэффициент регрессии а1 показывает, на сколько (в абсолютном выражении) изменится результативный признак у при изменении факторного признака х на единицу.

Если а1 имеет положительный знак, то связь прямая, если отрицательный – связь обратная.

Параметры уравнения связи определяются способом (методом) наименьших квадратов (МНК) с помощью составленной и решенной системы двух уравнений с двумя неизвестными:

где n – число членов в каждом из двух сравниваемых рядов (число единиц совокупности);
Σx – сумма значений факторного признака;
Σx 2 – сумма квадратов значений факторного признака;
Σy – сумма значений результативного признака;
Σyx – сумма произведений значений факторного признака на значения результативного признака.

Для справки: суть метода наименьших квадратов заключается в следующем требовании: искомые теоретические значения результативного признака должны быть такими, при которых бы обеспечивалась минимальная сумма квадратов их отклонений от эмпирических значений.

Решив систему уравнений, получаем значения параметров уравнения связи, определяемые по формулам:

Если параметры уравнения определены правильно, то Σу = Σ y x.

Пример построения уравнения парной линейной регрессии

По данным таблицы 8.1 необходимо построить линейное уравнение регрессии, характеризующее зависимость выпуска продукции десяти предприятий одной отрасли от стоимости их основных производственных фондов.

Данные, характеризующие десять предприятий одной отрасли

Номер предприятия12345678910
Стоимость ОПФ, млрд. руб.12810691511131410
Выпуск продукции, млрд. руб.5,64,04,02,43,65,04,66,57,04,5

Для расчета параметров уравнения регрессии и выровненных по х значений у построим вспомогательную таблицу 8.2.

Данные, используемые для расчета параметров линейного уравнения связи стоимости основных производственных фондов и выпуска продукции десяти предприятий отрасли

№ завода (n)Стоимость ОПФ (х), млрд. руб.Выпуск продукции (у), млрд. руб.x 2xуy 2y x = 0,167 + 0,421x
1125,614467,231,365,2
2846432163,5
310410040164,4
462,43614,45,762,7
593,68132,412,964
615522575256,5
7114,612150,621,164,8
8136,516984,542,255,6
914719698496,1
10104,51004520,254,4
Всего10847,21236539,1239,7447,2
В среднем на 1 завод10,84,72123,653,9123,974х

По формуле 8.3 параметр уравнения прямой: a0 = 0,167.

По формуле 8.4 коэффициент регрессии: a1 = 0,421.

По формуле 8.1 линейное уравнение связи между стоимостью основных производственных фондов и выпуском продукции имеет вид: y x = 0,167 + 0,421x

Коэффициент регрессии а1 = 0,421 показывает, что при увеличении стоимости основных производственных фондов на 1 млрд. руб. выпуск продукции в среднем увеличится на 0,421 млрд. руб.

Последовательно подставляя в полученное уравнение значения факторного признака х, находим выровненные значения результативного признака y x, показывающие, каким теоретически должен быть средний размер выпущенной продукции при данном размере основных производственных фондов (при прочих равных условиях). Выровненные (теоретические) значения выпуска продукции приведены в последней графе таблицы 8.2.

Правильность расчета параметров уравнения подтверждает равенство Σу = Σ y x (47,2 = 47,2).

На рис. 8.2 представлены эмпирические, теоретические и средние уровни выпуска продукции предприятий отрасли, отличающихся по стоимости основных производственных фондов.

Для экономической интерпретации линейных и нелинейных связей между двумя исследуемыми явлениями часто используют рассчитанные на основе уравнений регрессии коэффициенты эластичности.

Коэффициент эластичности показывает, на сколько процентов изменится в среднем результативный признак у при изменении факторного признака х на 1%.

Для линейной зависимости коэффициент эластичности (ε) определяется:

– для отдельной единицы совокупности по формуле:

– в целом для совокупности по формуле:

Пример расчета коэффициентов эластичности

По данным таблицы 8.2 необходимо найти коэффициенты эластичности для отдельных предприятий и в среднем по отрасли.

По формуле 8.5 коэффициент эластичности на первом предприятии равен: ε1 = 0,97, т.е. 1% прироста стоимости основных производственных фондов обеспечивает прирост выпуска продукции на этом предприятии на 0,97%; …; на пятом предприятии – на 0,95%; …; на десятом предприятии – на 0,96%.

По формуле 8.6 коэффициент эластичности равен:

ε = 0,963. Это означает, что при увеличении стоимости основных производственных фондов в целом по предприятиям отрасли на 1%, выпуск продукции увеличится в среднем на 0,963%. Определение тесноты связи в корреляционно-регрессионном анализе основывается на правиле сложения дисперсий, как и в методе аналитической группировки. Но в отличие от него, где для оценки линии регрессии используют групповые средние результативного признака, в корреляционно-регрессионном анализе для этой цели используют теоретические значения результативного признака.

Наглядно представить и обосновать корреляционно-регрессионный анализ позволяет график.

На графике на рис. 8.2 проведены три линии: у – ломанная линия фактических данных; y x – прямая наклонная линия теоретических значений у при абстрагировании от влияния всех факторов, кроме фактора х (переменная средняя); y – прямая горизонтальная линия, из среднего значения которой исключено влияние на у всех без исключения факторов (постоянная средняя).

Несовпадение линии переменной средней y x с линией постоянной средней y поясняется влиянием факторного признака х, что, в свою очередь, свидетельствует о наличии между признаками у и х неполной, нефункциональной связи. Для определения тесноты этой связи необходимо рассчитать дисперсию отклонений у и y x, то есть остаточную дисперсию, которая обусловлена влиянием всех факторов, кроме фактора х. Разница между общей и остаточной дисперсиями дает теоретическую (факторную) дисперсию, которая измеряет вариацию, обусловленную фактором х.

На сопоставлении этой разницы с общей дисперсией построен индекс корреляции или теоретическое корреляционное отношение (R), которое определяется по формулам:

где σ 2 общ – общая дисперсия;
σ 2 ост – остаточная дисперсия;
σ 2 y x – факторная (теоретическая) дисперсия.

Факторную дисперсию по теоретическим значениям исчисляют по формуле:

Остаточную дисперсию определяют по формулам:

Коэффициент детерминации (R 2 ) характеризует ту часть вариации результативного признака у, которая соответствует линейному уравнению регрессии (т.е. обусловлена вариацией факторного признака) и исчисляется по формуле:

Индекс корреляции принимает значения от 0 до 1. Когда R = 0, то связи между вариацией признаков х и у нет. Остаточная дисперсия равняется общей, а теоретическая дисперсия равняется нулю. Все теоретические значения y x совпадают со средними значениями y , линия y x на графике совпадает с линией y , то есть принимает горизонтальное положение. При R = 1 теоретическая дисперсия равна общей, а остаточная равна нулю, фактические значения у совпадают с теоретическими y x, следовательно, связь между исследуемыми признаками линейно-функциональная.

Индекс корреляции пригоден для измерения тесноты связи при любой ее форме. Он, как и эмпирическое корреляционное отношение, измеряет только тесноту связи и не показывает ее направление.

Для измерения тесноты связи и определения ее направления при линейной зависимости используется линейный коэффициент корреляции (r), определяемый по формулам:

Значение r колеблется в пределах от -1 до +1. Положительное значение r означает прямую связь между признаками, а отрицательное – обратную.

Оценка тесноты связи между признаками проводится по данным таблицы 8.3.

Качественная оценка связи между признаками

Сила связиЗначение r при наличии
прямой связиобратной связи
Слабая0,1-0,3(-0,1)-(-0,3)
Средняя0,3-0,7(-0,3)-(-0,7)
Тесная0,7-0,99(-0,7)-(-0,99)

Проверка надежности (существенности) связи в корреляционно-регрессионном анализе осуществляют при помощи тех же самых критериев и процедур, что и в аналитической группировке.

Фактическое значение F-критерия определяют по формуле:

Степени свободы k1 и k2 зависят от числа параметров уравнения регрессии (m) и количества единиц исследуемой совокупности (n) и рассчитываются по формулам:

Надежность связи между признаками, т.е. надежность коэффициента детерминации R 2 проверяют при помощи таблицы по F-критерию для 5%-ного уровня значимости (см. табл. 7.10).

Для установления достоверности рассчитанного линейного коэффициента корреляции используют критерий Стьюдента, рассчитываемый по формуле

где μr – средняя ошибка коэффициента корреляции, рассчитываемая по формуле:

При достаточно большом числе наблюдений (n > 50) коэффициент корреляции можно считать достоверным, если он превышает свою ошибку в 3 и больше раз, а если он меньше 3, то связь между исследуемыми признаками у и х не доказана.

Пример расчета индекса корреляции (теоретического корреляционного отношения), коэффициента детерминации, линейного коэффициента корреляции и критериев Фишера и Стьюдента

По данным таблицы 8.2 необходимо оценить силу и направление связи между стоимостью основных производственных фондов предприятий и выпуском продукции, а также проверить надежность рассчитанного коэффициента детерминации и достоверность линейного коэффициента корреляции.

Для расчета индекса корреляции, используемого для оценки тесноты связи между результативным (выпуском продукции) и факторным (стоимостью ОПФ) признаками рассчитаем ряд вспомогательных показателей.

По формуле 8.9 по данным таблицы 7.15 факторная дисперсия равна: 1,238.

Общую дисперсию исчислим по данным таблицы 8.2, используя способ разности (формула 5.12): = 1,696 – 1,238 = 0,458.

Таким образом, по формулам 8.7 и 8.8 индекс корреляции равен: R = 0,854, что свидетельствует о тесной связи между выпуском продукции и стоимостью основных производственных фондов предприятий (см. табл. 5.10).

По формуле 8.12 коэффициент детерминации равен: 0,730. Это говорит о том, что в обследуемой совокупности предприятий 73,0% вариации выпуска продукции объясняется разным уровнем их оснащенности основными производственными фондами, т.е. вариация выпуска продукции на 73,0% обусловлена вариацией стоимости основных производственных фондов.

Для расчета линейного коэффициента корреляции, позволяющего оценить не только силу, но и направление связи между исследуемыми признаками, найдем ряд промежуточных показателей.

Преобразовав формулу 5.12 и используя данные таблицы 8.2, получим среднее квадратическое отклонение факторного признака: 2,638и среднее квадратическое отклонение результативного признака 1,302.

Таким образом, по формуле 8.13 (8.14) и данным таблицы 8.2 линейный коэффициент корреляции равен: 0,854, что подтверждает наличие тесной (сильной) прямой связи между стоимостью основных производственных фондов и выпуском продукции предприятий. Абсолютная величина линейного коэффициента корреляции практически совпадает с индексом корреляции (отклонение составляет 0,01).

Для оценки надежности связи между выпуском продукции и стоимостью основных производственных фондов предприятий найдем фактическое значение F-критерия.

Так как линейное уравнение имеет только два параметра, то по формуле 8.16 степень свободы k1 = 2 – 1 = 1, а потому, что обследованием было охвачено 10 предприятий по формуле 8.17 степень свободы k2 = 10 – 2 = 8.

По формуле 8.15 фактическое значение F-критерия равно: 19,68.

По данным таблицы 7.10 с вероятностью 0,95 критическое значение Fт = 5,32, что значительно меньше полученного фактического значения F-критерия. Это подтверждает надежность корреляционной связи между исследуемыми признаками.

Для установления достоверности рассчитанного линейного коэффициента корреляции найдем значение критерия Стьюдента. Для этого по формуле 8.19 исчислим среднюю ошибку коэффициента корреляции: 0,092.

По формуле 8.18 критерий Стьюдента равен: 9,27. Так как 9,27 > 3, то это дает основание считать, что рассчитанный линейный коэффициент корреляции достаточно точно характеризует тесноту связи между исследуемыми признаками.

Множественная регрессия

На практике на результативный признак, как правило, влияет не один, а несколько факторов.

Между факторами существуют сложные взаимосвязи, поэтому их влияние на результативный признак комплексное и его нельзя рассматривать как простую сумму изолированных влияний.

Многофакторный корреляционно-регрессионный анализ позволяет оценить степень влияния на исследуемый результативный показатель каждого из введенных в модель факторов при фиксированных на среднем уровне других факторах. При этом важным условием является отсутствие функциональной связи между факторами.

Математически задача корреляционно-регрессионного анализа сводится к поиску аналитического выражения, которое как можно лучше отражало бы связь факторных признаков с результативным признаком, т.е. к нахождению функции: y x = f(x1,x2,x3. xn).

Множественная регрессия – это уравнение статистической связи результативного признака (зависимой переменной) с несколькими факторами (независимыми переменными).

Наиболее сложной проблемой является выбор формы связи, выражающейся аналитическим уравнением, на основе которого по существующим факторам определяются значения результативного признака – функции. Эта функция должна лучше других отражать реально существующие связи между исследуемым показателем и факторами. Эмпирическое обоснование типа функции при помощи графического анализа связей для многофакторных моделей практически непригодно.

Форму связи можно определить путем перебора функций разных типов, но это связано с большим количеством лишних расчетов. Принимая во внимание, что любую функцию нескольких переменных можно путем логарифмирования или замены переменных привести к линейному виду, уравнение множественной регрессии можно выразить в линейной форме:

Параметры уравнения находят методом наименьших квадратов.

Так, для расчета параметров уравнения линейной двухфакторной регрессии, представленного формулой:

где y x – расчетные значения результативного признака-функции;
х1 и х2 – факторные признаки;
а0, а1 и а2 — параметры уравнения, методом наименьших квадратов необходимо решить систему нормальных уравнений:

Каждый коэффициент уравнения (а1, а2, …, аn) показывает степень влияния соответствующего фактора на результативный показатель при фиксированном положении остальных факторов, т.е., как изменится результативный показатель при изменении отдельного факторного показателя на единицу. Свободный член уравнения множественной регрессии экономического содержания не имеет.

Если, подставляя в уравнение регрессии значения х1 и х2, получаем соответствующие значения переменной средней, достаточно близко воссоздающие значения фактических уровней результативного признака, то выбор формы математического выражения корреляционной связи между тремя исследуемыми факторами сделан правильно.

Однако на основе коэффициентов регрессии нельзя судить, какой из факторных признаков больше влияет на результативный признак, поскольку коэффициенты регрессии между собой не сравнимы, ибо не сопоставимы по сути отражаемые ими явления, и они выражены разными единицами измерения.

С целью выявления сравнимой силы влияния отдельных факторов и резервов, заложенных в них, статистика рассчитывает частные коэффициенты эластичности, а также бета-коэффициенты.

Частные коэффициенты эластичности (εi) рассчитываются по формуле:

где аi – коэффициент регрессии при i-ом факторе;

x i – среднее значение i-го фактора;

y – среднее значение результативного фактора.

Бета-коэффициенты (βi) рассчитываются по формуле:

где σxi – среднее квадратическое отклонение i-го фактора;
σy – среднее квадратическое отклонение результативного признака.

Частные коэффициенты эластичности показывают, на сколько процентов в среднем изменится результативный признак при изменении на 1% каждого фактора и при фиксированном положении других факторов.

Для определения факторов, имеющих наибольшие резервы улучшения исследуемого признака, с учетом степени вариации факторов, положенных в уравнение множественной регрессии, рассчитывают частные β-коэффициенты, показывающие на какую часть среднего квадратического отклонения изменяется результативный признак при изменении соответствующего факторного признака на величину его среднего квадратического отклонения.

Для характеристики тесноты связи при множественной линейной корреляции используют множественный коэффициент корреляции (R), рассчитываемый по формуле:

где ryx1, ryx2, rx1x2 – парные коэффициенты линейной корреляции, позволяющие оценить влияние каждого фактора отдельно на результативный показатель, и определяемые по формулам:

Множественный коэффициент корреляции колеблется в пределах от 0 до + 1 и интерпретируется так же, как и теоретическое корреляционное отношение.

Совокупный коэффициент множественной детерминации показывает, какую часть общей корреляции составляют колебания под влиянием факторов х1, х2, …, хn, положенных в многофакторную модель для исследования.

На основе парных коэффициентов корреляции находятся частные коэффициенты корреляции первого порядка, показывающие связь каждого фактора с исследуемым показателем в условиях комплексного взаимодействия факторов, рассчитываемые по формулам

С целью более глубокого анализа взаимосвязи общественных явлений и их признаков увеличивают количество существенных факторов, включаемых в модель исследуемого показателя, и строят многофакторные уравнения регрессии. Их рассчитывают при помощи персональных компьютеров. Современнон программное обеспечение позволяет за относительно короткое время получить достаточно много вариантов уравнений. В ЭВМ вводятся значения зависимой переменной у и матрица независимых переменных х, принимается форма уравнения, например линейная. Ставится задача включить в уравнение k наиболее значимых х. В результате получим уравнение регрессии с k наиболее значимыми факторами. Аналогично можно выбрать наилучшую форму связи. Этот традиционный прием, называемый пошаговой регрессией, позволяет быстро и достаточно точно определиться с уравнением множественной регрессии.

Пример расчета параметров уравнения множественной регрессии, частных коэффициентов эластичности и бета-коэффициентов, множественного коэффициента корреляции и частных коэффициентов корреляции первого порядка

В таблице 8.4 представлены данные о производительности труда (выработке продукции на одного работающего), доле бракованной продукции в общем объеме ее производства и средней себестоимости 1 т продукции по двадцати пяти предприятиям, специализирующимся на выпуске кондитерских изделий (печенья в ассортименте).

Необходимо установить зависимость средней себестоимости 1 т продукции от двух факторов: выработки продукции на одного работающего и доли бракованной продукции в общем объеме ее производства. С целью выявления сравнимой силы влияния этих факторов, а также резервов повышения средней себестоимости 1 т продукции, заложенных в производительности труда и удельном весе брака, нужно рассчитать частные коэффициенты эластичности и бетакоэффициенты. Кроме того, следует оценить силу влияния обозначенных факторов, как по отдельности, так и вместе на заданный результативный признак, определить какую долю вариации средней себестоимости 1 т продукции обусловливают только выработка и только процент брака; охарактеризовать связь каждого фактора с исследуемым показателем в условиях комплексного взаимодействия факторов.

Данные, характеризующие работу предприятий одной отрасли хозяйственной деятельности кондитерских предприятий

№ предприятияВыработка продукции на одного работающего, тУдельный вес брака, %Средняя себестоимость 1 т продукции, руб.
nх1х2у
1234
114,64,22398
213,56,72546
321,65,52620
417,47,72514
544,81,21589
6111,92,21011
720,18,42598
828,11,41864
922,34,22041
1025,30,91986
1156,01,31701
1240,21,81736
1340,63,31974
1475,83,41721
1527,61,12018
1688,40,11300
1716,64,12513
1833,42,31952
1917,09,32820
2033,13,31964
2130,13,51865
2265,21,01752
2322,65,22386
2433,42,32043
2519,72,72050

Для расчета параметров уравнения линейной двухфакторной регрессии и теоретических значений результативного признака (средней себестоимости 1 т продукции) составим вспомогательную таблицу 8.5.

Данные для расчета параметров уравнения линейной двухфакторной регрессии и теоретические значения результативного признака – функции y x

nх1х2уу×х1у×х2х1 2х2 2y 2х1×х2y x
1234567891011
114,64,2239835010,810071,6213,1617,6575040461,322330
213,56,7254634371,017058,2182,2544,9648211690,452559
321,65,5262056592,014410,0466,5630,36864400118,802371
417,47,7251443743,619357,8302,7659,36320196133,982607
544,81,2158971187,21906,82007,041,4252492153,761756
6111,92,21011113130,92224,212521,614,81022121246,181152
720,18,4259852219,821823,2404,0170,66749604168,842640
828,11,4186452378,42609,6789,612,0347449639,341946
922,34,2204145514,38572,2497,2917,6416568193,662250
1025,30,9198650245,81787,4640,090,8394419622,771931
1156,01,3170195256,02211,33136,001,7289340172,801649
1240,21,8173669787,23124,81616,043,2301369672,361856
1340,63,3197480144,46514,21648,3610,93896676133,981983
1475,83,41721130451,85851,45745,6411,62961841257,721629
1527,61,1201855696,82219,8761,761,2407232430,361925
1688,40,11300114920,0130,07814,560,016900008,841211
1716,64,1251341715,810303,3275,5616,8631516968,062300
1833,42,3195265196,84489,61115,565,3381030476,821970
1917,09,3282047940,026226,0289,0086,57952400158,102751
2033,13,3196465008,46481,21095,6110,93857296109,232060
2130,13,5186556136,56527,5906,0112,33478225105,352109
2265,21,01752114230,41752,04251,041,0306950465,201528
2322,65,2238653923,612407,2510,7627,05692996117,522335
2433,42,3204368236,24698,91115,565,3417384976,821970
2519,72,7205040385,05535,0388,097,3420250053,192146
Всего919,387,1509621653422,7198293,248693,93450,31083783162435,4550962

В среднем на 1 предприятие х 36,8 3,5 2038 66136,9 7931,7 1947,76 18,01 4335133 97,42 2038

Подставим данные таблицы 8.5 в систему нормальных уравнений 8.22 и получим систему уравнений:

⌈ 50962 = 25 a0 + 919,3 a1 + 87,1 a2 ;
〈 165322,7 = 919.3 a0 + 48693.93 a1 + 2435,45 a2 ;
⌊ 198293,2 = 87,1 a0 + 2435,45 a1 + 450,3 a2 .

Таким образом, уравнение связи, определяющее зависимость средней себестоимости 1 т продукции предприятий (результативного признака) от производительности труда их работников и удельного веса брака (двух факторных признаков), имеет вид (формула 8.21):

Подставляя в полученное уравнение значения х1 и х2, получаем соответствующие значения переменной средней (последняя графа таблицы 7.18), которые достаточно близко воссоздают значения фактических уровней себестоимости продукции. Это свидетельствует про правильный выбор формы математического выражения корреляционной связи между тремя исследуемыми факторами.

Значения параметров уравнения линейной двухфакторной регрессии показывают, что с увеличением выработки одного работника на 1 т, средняя себестоимость 1 т продукции снижается на 10,31 руб., а при увеличении процента брака на 1, средняя себестоимость 1 т продукции возрастает на 87,40 руб.

Вместе с тем полученные значения коэффициентов регрессии не позволяют сделать вывод о том, какой из двух факторных признаков оказывает большее влияние на результативный признак, поскольку между собой эти факторные признаки несравнимы.

По формуле 8.23 на основании данных таблицы 8.5 и полученных значений коэффициентов регрессии рассчитаем частные коэффициенты эластичности:

Анализ частных коэффициентов эластичности показывает, что в абсолютном выражении наибольшее влияние на среднюю себестоимость 1 т продукции оказывает выработка работников предприятий – фактор х1, с увеличением которой на 1% средняя себестоимость 1 т продукции снижается на 0,19%. При увеличении удельного веса бракованной продукции на 1% средняя себестоимость 1 т продукции повышается на 0,15%.

Для расчета β–коэффициентов необходимо рассчитать соответствующие средние квадратические отклонения.

Преобразовав формулу 5.12 и используя данные таблицы 8.5, получим средние квадратические отклонения факторных признаков, а также среднее квадратическое отклонение результативного признака:

Тогда по формуле 8.24 значения β–коэффициентов равны:

Анализ β-коэффициентов показывает, что на среднюю себестоимость продукции наибольшее влияние (а значит и наибольшие резервы ее снижения) из двух исследуемых факторов с учетом их вариации имеет фактор х1 – выработка работников, ибо ему соответствует большее по модулю значение β-коэффициента.

Для характеристики тесноты связи между себестоимостью 1 т продукции, выработкой работников и удельным весом бракованной продукции используется множественный коэффициент корреляции, для расчета которого предварительно нужно получить парные коэффициенты корреляции.

По формулам 8.26-8.28 на основе данных таблицы 8.5 и значений средних квадратических отклонений факторных и результативного признаков парные коэффициенты корреляции соответственно равны:

Высокие значения парных коэффициентов корреляции свидетельствуют о сильном влиянии (отдельно) выработки работников и уровня брака на среднюю себестоимость 1 т продукции.

Отметим, что отрицательное значение парного коэффициента корреляции между факторными признаками свидетельствует об обратной зависимости между выработкой и количеством бракованной продукции. Тот факт, что парный коэффициент корреляции между выработкой работников и уровнем бракованной продукции равный -0,519, по модулю меньше 0,85 (см. рис. 8.1), говорит о правильном включении этих факторов в одну корреляционную модель.

По формуле 8.25 множественный коэффициент корреляции равен: Ryx1x2 = 0,822. Он показывает, что между двумя факторными и результативным признаками существует тесная связь.

Совокупный коэффициент множественной детерминации (0,676) свидетельствует про то, что вариация средней себестоимости 1 т продукции на 67,6% обусловлена двумя факторами, введенными в корреляционную модель: изменением выработки работников и уровня брака. Это означает, что выбранные факторы существенно влияют на исследуемый показатель.

На основе парных коэффициентов корреляции по формулам 8.29 и 8.30 рассчитаем частные коэффициенты корреляции первого порядка, отражающие связь каждого фактора с исследуемым показателем (средней себестоимостью 1 т продукции) в условиях комплексного взаимодействия факторов:


источники:

http://masters.donntu.org/2005/kita/tokarev/library/regress.htm

http://be5.biz/ekonomika/s015/8.html

© 2023 Русский язык. Привила написания. Наш первый проект тут и тут