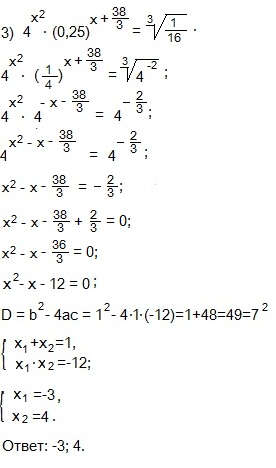Математика решение уравнений сводящихся к квадратным

Показательные уравнения, сводящиеся к квадратным

Разберем показательные уравнения, сводящиеся к квадратным. Их могут ученики кратко называть «квадратные показательные уравнения», хотя это название не точное. Однако, многие показательные уравнения заменой переменной сводятся к квадратному уравнению вида: ax 2 +bx+c=0.

Показательные уравнения, приводимые к квадратным на примерах

Уравнение 1

Решить уравнение:

1) 4 x +2 x+1 -3=0. Представим 4 x в виде степени с основанием 2.

(2 2 ) x +2 x ∙2 1 -3=0; при возведении степени в степень основание оставляют, а показатели перемножают: 2·х=х·2, поэтому:

вводим новую переменную: пусть 2 x =y;

y 2 + 2 y -3 =0.

Дискриминант для четного второго коэффициента: D₁=1 2 -1∙(-3)=1+3=4=2 2 – полный квадрат, поэтому применим теорему Виета: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Возвращаемся к переменной х:

1) 2 x =-3, нет решений, так как значения показательной функции: Е(у)=(0; +∞). (только положительные числа).

2) 2 x = 1. Число 1 можно представлять в виде нулевой степени по любому основанию.

2 x = 2 0 ;

Уравнение 2

2) 0,25 2x -5∙0,5 2x +4=0. Решаем аналогично. Представляем 0,25 2x — в виде степени с основанием 0,5.

(0,5 2 ) 2x -5∙0,5 2x +4=0;

(0,5 2x ) 2 -5∙0,5 2x +4=0.

0,5 2x =y; ввели новую переменную у и получили приведенное квадратное уравнение:

y 2 — 5 y+ 4 =0;

Дискриминант D=b 2 -4ac=5 2 -4∙1∙4=25-16=9=3 2 — полный квадрат, применяем теорему Виета: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

y₁+y₂= 5 , y₁+y₂= 4 . Корни приведенного квадратного уравнения находим подбором: y₁=1, y₂=4 и возвращаемся к переменной х:

1) 0,5 2x = 1 ; число 1 можно представлять в виде нулевой степени по любому основанию.

0,5 2x = 0,5 0 ;

2) 0,5 2 x =4; приведем степень 0,5 2 x к основанию 2, применив формулу: (1/a) x =а -х

2 -2 x =2 2 ; приравниваем показатели:

Уравнение 3

Представим левую и правую части в виде степеней с основанием 4, используя формулы: а -х =1/a x и a x ∙a y =a x + y .

Если равны две степени с одинаковыми основаниями, то основания можно опустить и приравнять показатели степеней. Переносим дробь из правой части равенства в левую и упрощаем левую часть.

Находим дискриминант приведенного квадратного уравнения. Дискриминант является квадратом целого числа, поэтому, подбираем корни, пользуясь теоремой Виета: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Итак, решение показательных уравнений, которое мы разбирали в предыдущем уроке, пополнилось еще одним методом — приведением показательного уравнения к обычному квадратному уравнению. Такие уравнения называют — показательные уравнения, сводящиеся к квадратным.

Решение уравнений, сводящихся к квадратным

Биквадратные уравнения

Биквадратным уравнением называется уравнение вида:

$$ ax^4+bx^2+c = 0, a \neq 0 $$

Алгоритм решения биквадратного уравнения

Шаг 1. Ввести новую переменную: $z = x^2 \ge 0$.

Переписать уравнение для новой переменной: $az^2+bz+c = 0$

Шаг 2. Решить полученное квадратное уравнение.

Если $D \gt 0$, $z_ <1,2>= \frac<-b \pm \sqrt> <2a>$. Проверить условие $z ≥ 0$, если положительных корней нет, решений нет, переход на шаг 4.

Если D = 0,$z_0 = -\frac<2a>$. Проверить условие $z \ge 0$, если корень отрицательный, решений нет, переход на шаг 4.

Если $D \lt 0$, решений нет, переход на шаг 4.

Шаг 3.Если после шага 2 остались положительные корни, найти x: $x = \pm \sqrt$.

Шаг 4. Работа завершена.

Шаг 1. $z = x^2 \ge 0, z^2+7z-30 = 0$

$z_1 = -10 \lt 0, z_2 = 3 \gt 0 $

Шаг 3. Находим корни из положительного $z: x_ <1,2>= \pm \sqrt<3>$

Метод разложения на множители

Решение уравнений, в которые переменная x входит с различными натуральными степенями и вещественными коэффициентами, по существу, является поиском корней многочлена.

Число $x_0$ называют корнем многочлена $P_n (x) = a_n x^n+a_ x^ + ⋯ + a_1 x+a_0$ если $P_n (x_0 ) = 0$.

Для многочлена $P_n$ (x) произвольной степени n справедливо следующее.

Если $x = x_0$ является корнем многочлена $P_n$ (x), то $P_n (x) = (x-x_0) P_ (x)$, где $P_ (x)$ — многочлен степени n-1.

Таким образом, разными способами находя корни и формируя скобки, можно постепенно добиваться понижения степени «оставшегося» многочлена, пока не будут найдены все корни.

При разложении многочлена

множители вида (x-a) называют линейными множителями ;
множители вида $ (x^2+bx+c)$, для которых $D \lt 0$, называют неприводимыми квадратичными множителями .

Любой многочлен $P_n$ (x) можно представить в виде конечного числа линейных и/или неприводимых квадратичных множителей.

Причём, такое представление единственно с точностью до порядка множителей.

Для разложения многочленов на множители применяются разные методы:

вынесение общего множителя за скобку (см. §19 справочника для 7 класса);
группировка (см. §20 справочника для 7 класса);
формулы сокращенного умножения (см. §25 справочника для 7 класса);
метод неопределённых коэффициентов;
выделение полного квадрата и т.п.

Решим уравнение $2x^3-x^2-8x+4 = 0$.

Раскладываем на множители: $x^2 (2x-1)-4(2x-1) = 0$

$$ (x^2-4)(2x-1) = 0 \Rightarrow (x-2)(x+2)(2x-1) = 0 $$

Корни уравнения: $x_1 = 2, x_2 = -2, x_3 = \frac<1><2>$

Метод замены переменной

Замена переменной – это уравнение, с помощью которого можно упростить исходное уравнение, и перейти к решению системы из двух более простых уравнений:

$Исходное \quad сложное \quad уравнение \iff <\left\< \begin Новая \quad переменная \quad (урав. \quad связи \quad со \quad старой \quad переменной \\ Исходное \quad урав. \quad в \quad «упрощ.» \quad виде \end \right.>$

Например, для биквадратных уравнений:

$$ ax^4+bx^2+c = 0 \iff <\left\< \begin z = x^2 \ge 0 \\ az^2+bz+c = 0 \end \right.> $$

Можно предложить аналогичные схемы для других уравнений:

$$ ax+b \sqrt+c = 0 \iff <\left\< \begin z = \sqrt \ge 0 \\ az^2+bz+c = 0 \end \right.> $$

И, в общем виде, для любой рациональной степени n:

$$ ax^<2n>+bx^n+c = 0 \iff <\left\< \begin z = x^n \\ az^2+bz+c = 0 \end \right.> , n \in \Bbb Q $$

В других случаях замена переменной не настолько очевидна.

Но при удачном выборе, этот метод очень упрощает задачу.

Раскроем скобки:$ x^2-x = \frac<24>$. Сделаем замену:

$$ z = \frac<24> \Rightarrow z(z-2) = 24 \Rightarrow z^2-2z-24 = 0 \Rightarrow (z-6)(z+4) = 0 \Rightarrow \left[ \begin z_1 = -4 \\ z_2 = 6 \end \right.$$

Возвращаемся к исходной переменной x:

$$ \left[ \begin x^2-x = -4 \\ x^2-x = 6 \end \right. \Rightarrow \left[ \begin x^2-x+4 = 0 \\ x^2-x-6 = 0 \end \right. \Rightarrow \left[ \begin D \lt 0, x \in \varnothing \\ (x-3)(x+2) = 0 \end \right. \Rightarrow \left[ \begin x_1 = -2 \\ x_2 = 3 \end \right. $$

При использовании метода замены переменной не забывайте возвращаться к исходной переменной.

Выделение полного квадрата

Метод выделения полного квадрата является одним из методов разложения на множители. Его идея – представить многочлен в виде разности квадратов двух других многочленов степенью пониже, и разложить разность на две скобки:

$$ P_n (x) = Q_k^2 (x)-R_m^2 (x) = (Q_k (x)-R_m (x))(Q_k (x)+R_m (x)) $$

Такое разложение не всегда возможно.

Рассмотрим выделение полного квадрата для квадратного трёхчлена:

$$ = a \Biggl(x+\frac <2a>\Biggr)^2 — \frac <4a>= a \Biggl(x+ \frac <2a>\Biggr)^2- \frac<4a>, D = b^2-4ac $$

Нами выделен полный квадрат $(x+\frac<2a>)^2$.

Данное выражение используется для построения и анализа графиков парабол (см. §28 данного справочника).

А его разложение на две линейные скобки, известное как теорема Виета (см. §26 данного справочника), возможно только при условии $D \ge 0$.

Решить уравнение $x^4+4x^2-1 = 0$

Выделим полный квадрат и разложим на множители:

$$ \left[ \begin x^2+2-\sqrt <5>= 0 \\ x^2+2+\sqrt <5>= 0 \end \right. \Rightarrow \left[ \begin x^2 = \sqrt <5>-2 \gt 0 \\ x^2 = -(2+\sqrt<5>) \lt 0 \end \right. \Rightarrow x_1,2 = \pm \sqrt<\sqrt<5>-2> $$

Примеры

Пример 1. Решите биквадратные уравнения:

Делаем замену: $2x^4+7x^2-4 = 0 \iff <\left\< \begin z = x^2 \ge 0 \\ 2z^2+7z-4 = 0 \end \right.>$

Решаем квадратное уравнение: $D = 7^2-4 \cdot 2 \cdot (-4) = 49+32 = 81 = 9^2$

$$ z = \frac<-7 \pm 9> <4>= \left[ \begin z_1 = -4 \lt 0 \\ z_2 = \frac<1> <2>\gt 0 \end \right. $$

Выбираем положительный z и возвращаемся к исходной переменной x:

Делаем замену: $(x+3)^4-10(x+3)^2+24 = 0 \iff <\left\< \begin z = (x+3)^2 \ge 0 \\ z^2-10z+24 = 0 \end \right.>$

Решаем квадратное уравнение: $z^2-10z+24 = 0 \Rightarrow (z-4)(z-6) = 0 \Rightarrow \left[ \begin z_1 = 4 \\ z_2 = 6 \end \right.$

Берём оба корня и возвращаемся к исходной переменной.

$$ \left[ \begin (x+3)^2 = 4 \\ (x+3)^2 = 6 \end \right. \Rightarrow \left[ \begin x+3 = \pm \sqrt <4>\\ x+3 = \pm \sqrt <6>\end \right. \Rightarrow \left[ \begin x_ <1,2>= -3 \pm 2 \\ x_ <3,4>= -3 \pm \sqrt <6>\end \right. \Rightarrow \left[ \begin x_1 = -5 \\ x_2 = -1 \\ x_ <3,4>= -3 \pm \sqrt <6>\end \right. $$

Пример 2. Решите уравнения аналогичные биквадратным:

Делаем замену: $x+4 \sqrt-60 = 0 \iff <\left\< \begin z = \sqrt \ge 0 \\ z^2+4z-60 = 0 \end \right.>$

Решаем квадратное уравнение: $ z^2+4z-60 = 0 \Rightarrow (z+10)(z-6) = 0 \Rightarrow \left[ \begin z_1 = -10 \\ z_2 = 6 \end \right.$

Выбираем положительный корень и возвращаемся к исходной переменной:

Делаем замену: $(x-1)^6-7(x-1)^3-8 = 0 \iff <\left\< \begin z = (x-1)^3 \\ z^2-7z-8 = 0 \end \right.>$

Решаем квадратное уравнение: $ z^2-7z-8 = 0 \Rightarrow (z+1)(z-8) = 0 \Rightarrow \left[ \begin z_1 = -1 \\ z_2 = 8 \end \right.$

При замене куба знак z может быть любым, берём оба корня и возвращаемся к исходной переменной.

$$ \left[ \begin (x-1)^3 = -1 \\ (x-1)^3 = 8 \end \right. \Rightarrow \left[ \begin x-1 = -1 \\ x-1 = 2 \end \right. \Rightarrow \left[ \begin x_1 = 0 \\ x_2 = 3 \end \right. $$

Пример 3. Решите уравнения с помощью замены переменной:

Заметим, что $(x+3)^2 = x^2+6x+9$. Получаем:

$$ (x^2+6x)^2-(x^2+6x+9) = 33 \Rightarrow (x^2+6x)^2-(x^2+6x)-42 = 0 $$

Решаем квадратное уравнение: $ z^2-z-42 = 0 \Rightarrow (z+6)(z-7) = 0 \Rightarrow \left[ \begin z_1 = -6 \\ z_2 = 7 \end \right.$

Берём оба корня и возвращаемся к исходной переменной.

$$ \left[ \begin x^2+6x = -6 \\ x^2+6x = 7 \end \right. \Rightarrow \left[ \begin x^2+6x+6 = 0 \\ x^2+6x-7=0 \end \right. \Rightarrow \left[ \begin D = 12, x = \frac<-6 \pm 2 \sqrt<3>> <2>\\ (x+7)(x-1) = 0 \end \right. \Rightarrow \left[ \begin x_ <1,2>= -3 \pm \sqrt <3>\\ x_3 = -7 \\ x_4 = 1 \end \right. $$

Делаем замену: $ \frac<4> + \frac<5> = 2 \iff \left[ \begin z = x^2+3 \ge 3 \\ \frac<4> + \frac<5> = 2 \end \right.$

Решаем уравнение относительно z:

$$ \frac<4> + \frac<5> = 2 \Rightarrow \frac<4(z+1)+5z> = \frac<2> <1>\Rightarrow 4(z+1)+5z = 2z(z+1) $$

$$ 2z^2+2z-9z-4 = 0 \Rightarrow 2z^2-7z-4 = 0 $$

$$ D = 7^2-4 \cdot 2 \cdot (-4) = 49+32 = 81 = 9^2 $$

$$ z = \frac<7 \pm 9> <4>= \left[ \begin z_1 = — \frac<1> <2>\lt 3 \\ z_2 = 4 \gt 3 \end \right. $$

Выбираем корень больше 3 и возвращаемся к исходной переменной:

$$ x^2+3 = 4 \Rightarrow x^2 = 1 \Rightarrow x_ <1,2>= \pm 1$$

Пример 4*. Решите уравнения:

Приведём это уравнение к биквадратному.

В линейных множителях (x+a) выберем все a =

Найдем их среднее арифметическое (см. §52 справочника для 7 класса)

Замена переменных $z = x+a_$:

Упрощаем уравнение, используя формулу разности квадратов:

$$ (z^2-9)(z^2-1) = 945 \Rightarrow z^4-10z^2+9 = 945 \Rightarrow z^4-10z^2-936 = 0 $$

Получили биквадратное уравнение.

Делаем замену: $z^4-10z^2-936 = 0 \iff <\left\< \begin t = z^2 \ge 0 \\ t^2-10t-936 = 0 \end \right.> $

Решаем квадратное уравнение:

$$ D = 100+4 \cdot 936 = 3844 = 62^2, t = \frac<10 \pm 62> <2>= \left[ \begin t_1 = -26 \lt 0 \\ t_2 = 36 \gt 0 \end \right. $$

Выбираем положительный корень и возвращаемся к переменной z:

$$ z = \pm \sqrt= \pm \sqrt <36>= \pm 6 $$

Возвращаемся к исходной переменной x:

$$ x = z-4 = \pm 6-4 = \left[ \begin x_1 = -10 \\ x_2 = 2 \end \right. $$

$$ z- \frac<1> =2,1 |\times z (z \neq 0) $$

$$ z^2-2,1z-1 = 0 \Rightarrow D = 2,1^2+4 = 8,41 = 2,9^2; z = \frac<2,1 \pm 2,9> <2>= \left[ \begin z_1 = -0,4 \\ z_2 = 2,5 \end \right. $$

Берём оба корня и возвращаемся к исходной переменной.

$$ \left[ \begin \frac = -0,4 \\ \frac = 2,5 \end \right. \Rightarrow \left[ \begin x^2+1 = -0,4x \\x^2+1 = 2,5x \end \right. \Rightarrow \left[ \begin x^2+0,4x+1 = 0 \\ x^2-2,5x+1 = 0 \end \right. $$

В первом уравнении $D = 0,4^2-4 \lt 0$, решений нет.

Во втором уравнении (x-2)(x-1/2) = 0 $\Rightarrow \left[ \begin x_1 = \frac<1> <2>\\ x_2 = 2 \end \right.$

Методы решения квадратных уравнений и уравнений, к ним сводящихся

Разделы: Математика

Планируя урок, мы рассматриваем его как целостную совокупность ориентированных на достижение определенной цели взаимодействующих управленческих функций, выполняемых одновременно или в некоторой последовательности. К этим управленческим функциям относятся:

планирование, то есть определение целей и средств их достижения;
организация, то есть создание и совершенствование взаимодействия между управляемой и управляющей системами для выполнения планов;
контроль, то есть сбор информации о процессе выполнения намеченных планов;
регулирование, то есть корректировка планов и процесса их реализации;
анализ, то есть изучение и оценка процесса результатов выполнения планов.

Этот вопрос можно решить при помощи организации уроков “по вертикали”, то есть уроков, на которых работают подгруппы разных классов, что позволяет старшим детям обратиться к ранее изученному материалу на другом качественном уровне, а младшим школьникам в диалоге со старшими товарищами систематизировать изученный материал и обобщить способы действия с ним. Варианты таких уроков:

– “Признаки равенства треугольников” в 7-м классе и “Признаки подобия треугольников” в 8-м классе;
– “Площади” в 8-й классе и “Площадь поверхности многогранников” в 11-й классе;
– “Формулы сокращенного умножения” в 7-м классе и “Действия с алгебраическими дробями” в 8-м классе; и т. д.

Одним из таких уроков является урок по теме “Методы решения квадратных уравнений и уравнений, к ним сводящимся”, который проводится по окончании изучения темы “Квадратные уравнения” в 8-м классе и в теме “Повторение” в 11-м классе. Уравнения и неравенства – наиболее распространенные типы задач, решаемых учащимися в школе. По сложившейся традиции эти задачи всегда предлагаются и на школьных выпускных экзаменах и на вступительных экзаменах в вузы. В связи с тем, что изменяется форма проведения экзаменов в виде тестов, возникает еще одна проблема: надо научить учащихся быстро находить правильный ответ.

Цель урока: Использовать квадратное уравнение как модель, описывающую различные зависимости между величинами.

научить учащихся использовать данную модель для планирования своей работы;
анализировать математическую модель с точки зрения поиска рациональных методов решения;
формировать целостное представление о применении данной математической модели;
показать применение данной математической модели в других темах математики.

Данному уроку предшествовал урок – зачет, когда учащиеся 8-го класса отвечали на заранее определенные вопросы учащимся 11-го класса, работая в парах:

1. Какие уравнения называются квадратными?

2. Какое квадратное уравнение называется полным, неполным?

3. Какое уравнение называется приведенным, не приведенным?

4. Является ли квадратным каждое из следующих уравнений:

5. Решите уравнения:
а) 3х 2 –21=0 б) 0,5х 2 –2=0 в) 5х 2 –8х=0

6. Может ли уравнение вида ах 2 +с=0 не иметь действительных корней?

7. Может ли неполное квадратное уравнение быть приведенным?

8. Какое выражение называется дискриминантом?

9. Напишите формулы для нахождения корней квадратного уравнения.

10. Решите квадратные уравнения:
а) 3х 2 –5х+2=0 б) 3m 2 x 2 –mx–4=0 в) (m+n)y 2 –2my+m–n=0

11.Решите относительно z уравнение: (a–z):(1–az)=(1–bz):(b–z)

12. Как по дискриминанту определить, сколько и каких корней имеет квадратное уравнение?

13.Как читается теорема Виета?

14. Как читается обратная теорема Виета?

15. Как, не решая уравнения, определить знаки его корней?

16. Каков порядок составления квадратных уравнений по известным его корням?

17. Один из корней уравнения х 2 – 6х – q = 0 больше другого на 2. Найдите q.

18. Определите знаки корней, не решая уравнений:

a) 4х 2 –11х+7=0 б) Зх 2 – 8х + 6 =0 в) 9х 2 – 6х + 1 = 0 г) х 2 + 2х – 15 = 0

19. Найдите корни уравнений, воспользовавшись теоремой Виета:

а) х 2 – х – 6 = 0 б) z 2 +2az–8a 2 =0

20. При каком условии сумма корней уравнения х 2 + рх + q = 0 равна их произведению?

21. Что называют квадратным трехчленом?

22. Как разложить квадратный трехчлен на множители?

23. Разложите на множители трехчлены: 2х 2 + 5х – 3; х 2 – х – 56.

24. Какие уравнения называются биквадратными?

Второй этап работы – урок–обобщение, когда при той же парной работе материал темы был систематизирован в схемах и таблицах, которые далее прилагаются к материалам. Эти таблицы определяют основное содержание структуры всей темы, в них включены формулы рационального счета, не пользующиеся широкой известностью, но часто спасающие учащихся на вступительных экзаменах в вузы от громоздких вычислений и экономящих время на решение более сложных задач.

Третий этап – повторительно-обобщающий урок, где реализуется работа с моделью квадратного уравнения.

Рассмотрим реализацию основных направлений учебно-управленческих умений на предлагаемом уроке:

Планирование осуществлялось через:

справочник, где материал систематизирован в схемах и таблицах, которые определяют основное содержание структуры всей темы;
работу с одной моделью;
использование модели для планирования своей работы;
формирование целостного представления о применении данной модели.

Организация осуществлялась при помощи:

работы в парах;
четкой постановки целей.

1. Обобщить и повторить методы решения квадратных уравнений и уравнений, сводящихся к ним.

2. Увидеть использование этих методов при решении уравнений в других темах алгебры старших классов.

Для 11-го класса:

1. Повторить рациональные методы решения квадратных уравнений и уравнений, сводящимся к ним, для подготовки к тестированию по алгебре и началам анализа.
2. Разделить обязанности при работе над уравнением.

решения восьмиклассников проверяют старшеклассники, а одиннадцатиклассники рассказывают, как они решают незнакомые для восьмиклассников уравнения (взаимоконтроль);
проверка решения группы (пары) всеми учащимися.

через систему жетонов;
безнаказанность ошибочного решения;
поощрение верных идей по поиску рациональных способов решения, по поиску ошибки.

анализ модели с точки зрения поиска рациональных способов решений;
подведение итогов урока: Что узнали восьмиклассники? Что узнали одиннадцатиклассники? Что дала работа в парах?

На уроке учащиеся работают парами восьмиклассник — одиннадцатиклассник, задачей которых является быстро и правильно отвечать на поставленные вопросы и зарабатывать баллы, из которых в конце урока складывается их совместная оценка.

Какие виды квадратных уравнений вам известны?

Учащиеся перечисляют известные им виды уравнений и получают задание: заполнить таблицу, распределив уравнения по видам.

Уравнение

Полное

Неполное

Приведенное

7х 2 +9х+2=0

y 2 –3у–4=0

ax 2 –1=0

x 2 – 5? x? =0

m 2 + –5=0

6x 2 +x=0

x 2 –3x–5–=0

5m 2 +2(–1)m+7=0

8x 2 –0,75=0,53

x 2 :3=3

2p 2 –3? p? –2=0

Таблицу заполняют учащиеся 8-го класса, а учащиеся 11-го класса производят контроль. У доски одна пара выполняет такую же работу, затем класс проверяет правильность заполнения таблицы.

II. Занятие проводится в форме аукциона. Товаром на аукционе являются уравнения. Каждая пара, согласовав свое решение, может купить лот, стоимость которого от 1 до 5 баллов. Тот, кто дает максимальную цену, рассказывает решение уравнения, зарабатывая стоимость лота. В случае ошибочного решения часть баллов снимается.

Предлагается устно решить уравнение х 2 – 8х – 20 = 0. Учитель предлагает купить лот, не показывая вида уравнения. Кто из учащихся первым дает большее количество баллов, тот становится покупателем. К доске выходит пара. восьмиклассник подробно объясняет решение уравнения, а одиннадцатиклассник следит за решением, и если есть замечания, то дополняет.

Выставляется на продажу задание: Определяя, имеет ли квадратное уравнение 2х 2 + 5х – 7 = 0 корни, учащиеся дали два решения:

1). Так как а = 2, b = 5, с= 7, D= 81, D > 0, значит, уравнение имеет два корня.
2). Так как а > 0, с 0.Уравнение имеет два корня.

Кто решил верно?

К доске выходит пара, которая купила этот лот. Восьмиклассник комментирует решение, выбирает рациональный способ. Одиннадцатиклассник следит за ответом, помогает, поправляет.

Продается «кот в мешке».

На продажу выставляются 3 уравнения, которые надо решить рациональным способом, но лот предлагается купить, не видя уравнений.

1). 1999у 2 –1997у–2=0

Ученик должен решить его так:

Т.к. 1999 + (–1997) + (–2) = 0, то у₁ = 1, у₂ = с/а, т.е. у₂ = –2/1999.

2). 67х 2 –106х–173=0

Ученик должен решить его так:

3). 2z 2 –11z + 12 = 0

Ученик должен рассуждать так: 2z 2 –11z+12=0, z 2 – 11z + 24 = 0. По теореме, обратной теореме Виета т₁ = 8, т₂ = 3. Корни искомого уравнения будут равны: z₁=8/2 =4 и z₂=3/2=1,5

Разыгрываются два уравнения, которые предлагаются решить всем письменно рациональными способами. Каждое уравнение продается отдельно.

1. (х+5) 4 + 8(х+5) 2 –9=0

2. (4/49)у 2 + 9 + (12/7)у = 0

Две пары учащихся решают у доски эти уравнения.

Выставляется на продажу три уравнения. Каждая пара покупает одно из следующих уравнений, которое она должна решить

1. 2001sin 2 x – 2000sinx – 1 = 0

Каждое уравнение, кроме того, решается на доске парами, причем первую часть решения выполняет старшеклассник, рассказывая восьмикласснику о своих действиях, а квадратное уравнение решает восьмиклассник, одиннадцатиклассник же выполняет роль контролера.

Подводя итог урока, выясняется, что нового узнали восьмиклассники, а что одиннадцатиклассники? Что дала работа в парах? Домашнее же задание дает возможность еще раз проанализировать работу на уроке, придумав уравнения по данной теме.

Еще в “Великой дидактике” Яном Амосом Коменским было заявлено, что альфой и омегой школы должно быть изыскание способа, при котором учащие меньше бы учили, а учащиеся больше бы учились. Реализация программы общеучебных умений является движением к новой парадигме познавательной компетентности, переходом школы от декларации “учись учиться” к реальному освоению учениками целостной системы методов познания.