Материальное уравнение для магнитного поля

Материальное уравнение для векторов магнитного поля

Вы будете перенаправлены на Автор24

Причины использования материального уравнения

Фундаментальным уравнением магнитостатики в дифференциальной форме, является выражение:

где $\overrightarrow$ — плотность тока. Уравнение (1) является полевым и применяется для описания магнитостатического поля. Однако, при рассмотрении конкретных примеров этого уравнения не достаточно, так ка уравнение (1) не содержит ни каких постоянных, которые характеризовали бы свойства среды, в которой возбуждается поле. Для того чтобы при описании поля учесть свойства вещества вводят уравнение, которое называют материальным уравнением для векторов магнитного поля.

Принципиальный способ получения материальных уравнений дают молекулярные теории поляризации, намагничивания и электрической проводимости среды. В основе этих теорий положены идеализированные модели вещества. К таким моделям применяют уравнения классической или квантовой механики методы статистической физики и находят связь между векторами магнитной индукции и напряжённостью магнитного поля. Получают более или менее сложные соотношения, которые и дополняют фундаментальные уравнения.

Материальное уравнение для векторов магнитного поля в простейшем случае

Самое простое материальное уравнение для векторов магнитного поля получено для слабых полей, которые медленно изменяются во времени и пространстве. В таком случае для изотропных неферромагнитных сред материальное уравнение имеет вид:

где $<\mu >_0$ — магнитная постоянная$,\mu $ — магнитная проницаемость среды, характеризующая магнитные свойства среды.

Учет магнитных свойств, феноменологически описываемых намагниченностью, содержится в магнитной проницаемости ($\mu $). Когда Максвелл в свою теорию вводил материальное уравнение вида (2), он рассматривал магнитную проницаемость среды как постоянную величину, введенную в теорию из опыта. Электронная теория показала, что материальное уравнение в виде (2) выполняется, если соблюдаются условия:

1. за время приблизительно равное собственному периоду внутриатомных колебаний поле должно изменяться мало;
2. поле должно изменяться на очень небольшую величину на расстояниях сравнимых с размерами атомов и молекул.

Готовые работы на аналогичную тему

Итак, обычно считают, что материальное уравнение (2) выполняется, если $\mu $ может зависеть от координат, но не зависит от времени и векторов поля. В поле отсутствуют магниты и ферромагнитные тела.

Для учета движения среды сводят к движению зарядов или токов в среде. Тогда уравнение (1) не изменяется, а материальное уравнение (2) становится зависимым от скорости движения среды и что существенно их усложнит.

Надо отметить, что уравнение (2), как и остальные материальные уравнения электромагнитного поля хоть и является весьма значимым в теории, но фундаментальным не является и общностью, такой как уравнение (1) не обладает.

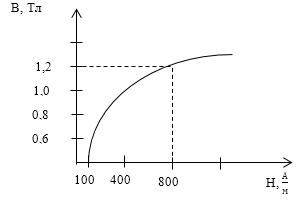
Задание: Определите индукцию магнитного поля (B) и намагниченность (J) сердечника тороида, который имеет N=151 виток. Средний радиус тороида R=3 см. Сила тока в тороиде I=1 А. Используйте график зависимости В(H) рис.1.

За основу решения задачи примем формулу, определяющую напряженность магнитного поля в тороиде:

где $n$ — число витков тороида на единицу длины. Найдем эту величину как:

Тогда выражение (1.1) примет вид:

Для того, чтобы далее воспользоваться графиком (рис.1) проведем вычисление напряженности поля:

Используя график получим, что при $H=800\frac<А><м>$ индукция магнитного поля В=1,2Тл.

Зная материальное уравнение для векторов магнитного поля, в применении к нашему случаю запишем его, как:

из уравнения (1.4) выразим магнитную проницаемость вещества:

Намагниченность связана с напряжением магнитного поля формулой:

\[J=\varkappa H=\left(\mu -1\right)H\left(1.6\right),\]

где $\varkappa $ магнитная восприимчивость. Используя (1.5), получим, что:

Вычислим магнитную проницаемость вещества:

Проведем вычисление намагниченности:

\[J=(1,19\cdot <10>^3-1)\cdot 800\approx 952\cdot 10^3(\frac<А><м>).\]

Ответ: В=1,2Тл, $J=952\cdot 10^3\frac<А><м>.$

Задание: Бесконечно длины соленоид находится в диамагнитной среде, длина соленоида равна l, площадь поперечного сечения S, число витков N. Индуктивность соленоида L, сила тока в нем I. Найдите намагниченность внутри соленоида и его магнитную индукцию.

Зная материальное уравнение, которое связывает напряжённость магнитного поля и индукцию для нашего соленоида:

напряжённость поля длинного соленоида:

и формулу для индуктивности соленоида:

найдем индукцию магнитного поля соленоида. Для этого выразим из (2.3) магнитную проницаемость среды, подставим ее в уравнение (2.1), так же подставим в (2.1) напряженность из (2.2), получим:

Вектор намагниченности связан с вектором напряженности, в нашем случае можно записать, что:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 11 02 2022

Лекция 24

1.Основные понятия

Основные законы электродинамики (уравнения Максвелла) были сформулированы в 1873 году. По своей значимости они аналогичны законам Ньютона в механике. Современная формулировка дана Герцем и Хевисайдом. Эти уравнения связывают характеристики электромагнитного поля и его источники.

В данные уравнения входят — напряженность электрического поля, индукция магнитного поля. Эти величины являются основными, т.к. определяют силу, действующую на заряженную частицу (Fл) – силу Лоренца.

Входят две вспомогательные величины — индукция электрического поля и — напряженность магнитного поля. Также входят — плотность тока и ρ — плотность заряда.

Уравнения Максвелла позволяют по известному полю найти токи и заряды (достаточно просто), а также по известным токам и зарядам найти поле (сложно). Уравнения будем писать в СИ в порядке указанном в физической энциклопедии.

2.Интегральная форма

I уравнение представляет собой обобщение закона полного тока.

Закон: Циркуляция напряженности магнитного поля по произвольному замкнутому контуру определяется током проводимости и быстротой изменения потока электрической индукции через произвольную поверхность, охваченную данным контуром.

II уравнение обобщает закон электромагнитной индукции.

Закон: Циркуляция напряженности электрического поля по произвольному замкнутому контуру определяется быстротой изменения потока магнитной индукции через площадку, охваченную данным контуром, взятой с обратным знаком

III уравнение: теорема Гаусса для электрической индукции.

Закон: Поток электрической индукции через произвольную замкнутую поверхность определяется зарядом внутри этой поверхности.

IV уравнение: закон Гаусса для индукции магнитного поля.

Закон: Поток индукции магнитного поля через произвольную замкнутую поверхность равен нулю.

3.Дифференциальная форма

Используя формулы Остроградского-Гаусса и Стокса можно получить

I уравнение Максвелла.

II уравнение Максвелла.

III уравнение Максвелла.

IV уравнение Максвелла

4.Материальные уравнения

В систему уравнений Максвелла входят 16 скалярных функций координат и времени. Самих уравнений – 8.

Чтобы замкнуть эту систему, используют материальные уравнения.

Величины e, μ, σ получаются из других разделов физики или определяются экспериментально.

Уравнения Максвелла

Уравнения Максвелла — это 4 уравнения, которые описывают, как электрические и магнитные поля распространяются и взаимодействуют; т.е. эти уравнения (правила или даже законы) описывают процессы/взаимодействия электромагнетизма.

Эти правила описывают, как проходит управление поведением электрических и магнитных полей. Уравнения Максвелла показывают, что электрический заряд (положительный и отрицательный):

1. Порождает электрическое поле (также если заряд изменяется со временем, то он вызывает появление электрического поля).
2. В дальнейшем он вызывает появление магнитного поля.

Уравнения Максвелла в дифференциальной форме

Уравнение 1: Закон Гаусса или Теорема Гаусса

Дивергенция электрического поля равняется плотности заряда. Существует вязь между электрическим полем и электрическим зарядом.

Дивергенция в физике показывает, насколько данная точка пространства является источником или потребителем потока поля.

Очень кратко: Электрические поля расходятся от электрических зарядов: электрический заряд создаёт поле вокруг себя и, таким образом, действует как источник электрических полей. Это можно сравнить с краном, который является источником воды.

Ещё закон Гаусса говорит о том, что отрицательные заряды действуют как сток для электрических полей (способ, как вода стекает через отверстие стока). Это означает, что линии электрического поля имеют начало и поглощаются при электрическом заряде.

Заряды с одинаковым знаком отталкиваются друг от друга, а противоположные заряды притягиваются друг к другу (если есть два положительных заряда, они будут отталкиваться; а если есть один отрицательный и один положительный, они будут притягиваться друг к другу).

Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)

Можно создать электрическое поле, изменив магнитное поле.

Очень кратко: Закон Фарадея гласит, что изменяющееся магнитное поле внутри контура вызывает индуцированный ток, который возникает из-за силы или напряжения внутри контура. Это значит:

1. Электрический ток порождает магнитные поля, а эти магнитные поля (вокруг цепи) вызывают электрический ток.
2. Изменяющееся во времени магнитное поле вызывает распространение электрического поля.
3. Циркулирующее во времени электрическое поле вызывает изменение магнитного поля во времени.

Уравнение 3: Закон Гаусса для магнетизма

Дивергенция магнитного потока любой замкнутой поверхности равна нулю. Магнитного монополя не существует.

Закон Гаусса для магнетизма утверждает (очень кратко):

1. Магнитных монополей не существует.
2. Расхождение полей B или H всегда равно нулю в любом объёме.
3. На расстоянии от магнитных диполей (это круговой ток) магнитные поля текут по замкнутому контуру.

Уравнение 4: Закон Ампера

Магнитное поле создаётся с помощью тока или изменяющегося электрического поля.

Очень кратко: Электрический ток порождает магнитное поле вокруг тока. Изменяющийся во времени электрический поток порождает магнитное поле.

Уравнения Максвелла в интегральной и дифференциальной форме

Вспомним сначала в дифференциальной форме и следом будет в интегральной форме.

Уравнение 1: Закон Гаусса (Теорема Гаусса)

Это же уравнение в интегральной форме:

Поток вектора электрической индукции D через любую замкнутую поверхность равняется сумме свободных зарядов, охваченных этой поверхностью. Электрическое поле создаётся нескомпенсированными электрическими зарядами (это те, что создают вокруг себя своё собственное электрическое поле).

Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)

И это же уравнение в интегральной форме:

Циркуляция вектора напряжённости Е вихревого электрического поля (по любому замкнутому контуру) равняется скорости изменения магнитного потока через площадь контура (S) с противоположным знаком.

Уравнение 3: Закон Гаусса для магнетизма

И это же уравнение в интегральной форме:

Силовые линии магнитного поля замкнуты, т.к. поток вектора индукции В магнитного поля через любую замкнутую поверхность равняется нулю.

Уравнение 4: Закон Ампера

И это же уравнение в интегральной форме:

Циркуляция вектора напряжённости Н магнитного поля по замкнутому контуру равняется алгебраической сумме токов, которые пронизывают этот контур. Магнитное поле создаётся не только током проводимости, но и переменным электрическим полем.