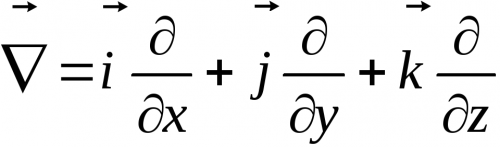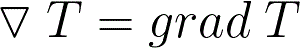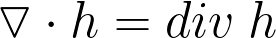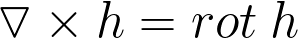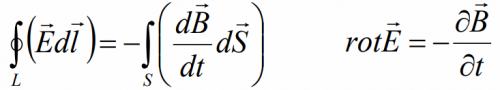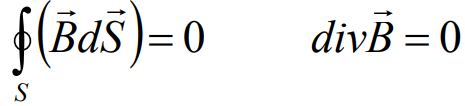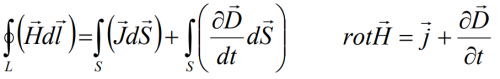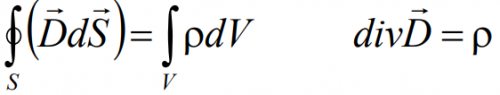Векторы электрического и магнитного полей. Материальные уравнения

Электрическое поле – особая форма материи, оказывающая силовое воздействие на электрические заряды. Магнитное поле – особая форма материи, оказывающая силовое воздействие на движущиеся электрические заряды. Электрическое и магнитное поля характеризуют с помощью силовых векторов.

Напряженность электрического поля Е определяют как силу, с которой электрическое поле действует на точечный положительный единичный заряд:

(1.1)

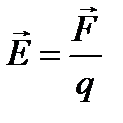
Магнитная индукция определяется как сила, действующая со стороны магнитного поля на заряд единичной величины, движущийся с единичной скоростью:

(1.2)

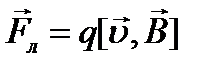
Напряженность электрического поля в различных средах различна. Это объясняется следующим образом. Под действием электрического поля вещество создает собственное поле (поляризуется). Собственное поле вещества накладывается на внешнее, изменяя его.

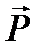
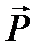
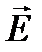
Для характеристики поляризации вводят вектор поляризованности . При не очень сильном внешнем поле величину вектора поляризованности можно считать пропорциональной напряженности электрического поля:

= ε₀χ (1.3)

Входящий в формулу (1.3) безразмерный параметр χ характеризует среду и называется диэлектрической восприимчивостью среды.

При рассмотрении многих процессов удобно ввести вектор D, характеризующий независимое от свойств среды внешнее электрическое поле:

. (1.3)

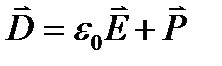
С учетом (1.2) формулу (1.3) можно представить в виде

, (1.4)

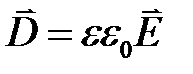
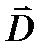
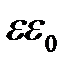
где ε = 1 + χ – относительная диэлектрическая проницаемость. Вектор принято называть вектором электрического смещения (электрической индукции). Иногда в литературе вводят абсолютную диэлектрическую проницаемость среды ε_А = .

Величина вектора 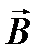зависит от свойств среды, поскольку под действием магнитного поля вещество намагничивается. В результате появляется дополнительное магнитное поле, которое налагается на первичное (явление, аналогичное поляризации вещества).

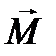
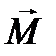
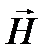
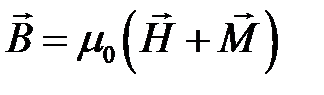
Намагниченность среды характеризуется вектором намагниченности . При рассмотрении многих процессов удобно вместо вектора ввести вектор , характеризующий независимое от свойств среды внешнее магнитное поле:

(1.5)

где μ₀ = 4π ∙ 10 -7 Гн/м – постоянная величина, называемая магнитной постоянной. Вектор 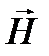принято называть вектором напряженности магнитного поля.

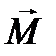
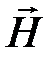
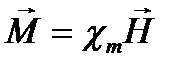
При не очень сильном внешнем магнитном поле можно считать, что вектор пропорционален вектору .

(1.6)

Безразмерный коэффициент 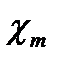называют магнитной восприимчивостью среды.

Подставляя формулу (1.6) в (1.5), получаем

(1.7)

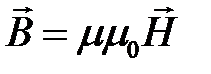
где μ = 1 + χ_m – абсолютная магнитная проницаемость среды. Иногда в литературе вводят абсолютную магнитную проницаемость среды μ_А = .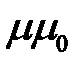

Под действием электрического поля в среде, обладающей проводимостью, возникает электрический ток (ток проводимости), распределение которого удобно характеризовать вектором плотности тока проводимости

(1.8)

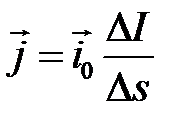
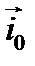
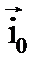
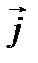
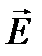
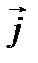
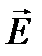
где – единичный вектор, показывающий направление тока (движения положительных зарядов) в рассматриваемой точке, Δs – плоская площадка, содержащая рассматриваемую точку, расположенная перпендикулярно вектору , ΔI – сила тока проводимости, протекающего через Δs.

Вектор связан с вектором соотношением

= σ , (1.9)

которое представляет собой закон Ома в дифференциальной форме. Коэффициент пропорциональности σ называют удельной проводимостью среды.

Система, состоящая из уравнений (1.4), (1.7), (1.9):

(1.10)

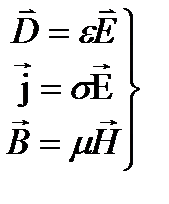
имеет большое значение при изучении электромагнитных явлений, их часто называют материальными уравнениями, поскольку они характеризуют среду.

Материальное уравнение для векторов магнитного поля

Вы будете перенаправлены на Автор24

Причины использования материального уравнения

Фундаментальным уравнением магнитостатики в дифференциальной форме, является выражение:

где $\overrightarrow$ — плотность тока. Уравнение (1) является полевым и применяется для описания магнитостатического поля. Однако, при рассмотрении конкретных примеров этого уравнения не достаточно, так ка уравнение (1) не содержит ни каких постоянных, которые характеризовали бы свойства среды, в которой возбуждается поле. Для того чтобы при описании поля учесть свойства вещества вводят уравнение, которое называют материальным уравнением для векторов магнитного поля.

Принципиальный способ получения материальных уравнений дают молекулярные теории поляризации, намагничивания и электрической проводимости среды. В основе этих теорий положены идеализированные модели вещества. К таким моделям применяют уравнения классической или квантовой механики методы статистической физики и находят связь между векторами магнитной индукции и напряжённостью магнитного поля. Получают более или менее сложные соотношения, которые и дополняют фундаментальные уравнения.

Материальное уравнение для векторов магнитного поля в простейшем случае

Самое простое материальное уравнение для векторов магнитного поля получено для слабых полей, которые медленно изменяются во времени и пространстве. В таком случае для изотропных неферромагнитных сред материальное уравнение имеет вид:

где $<\mu >_0$ — магнитная постоянная$,\mu $ — магнитная проницаемость среды, характеризующая магнитные свойства среды.

Учет магнитных свойств, феноменологически описываемых намагниченностью, содержится в магнитной проницаемости ($\mu $). Когда Максвелл в свою теорию вводил материальное уравнение вида (2), он рассматривал магнитную проницаемость среды как постоянную величину, введенную в теорию из опыта. Электронная теория показала, что материальное уравнение в виде (2) выполняется, если соблюдаются условия:

1. за время приблизительно равное собственному периоду внутриатомных колебаний поле должно изменяться мало;
2. поле должно изменяться на очень небольшую величину на расстояниях сравнимых с размерами атомов и молекул.

Готовые работы на аналогичную тему

Итак, обычно считают, что материальное уравнение (2) выполняется, если $\mu $ может зависеть от координат, но не зависит от времени и векторов поля. В поле отсутствуют магниты и ферромагнитные тела.

Для учета движения среды сводят к движению зарядов или токов в среде. Тогда уравнение (1) не изменяется, а материальное уравнение (2) становится зависимым от скорости движения среды и что существенно их усложнит.

Надо отметить, что уравнение (2), как и остальные материальные уравнения электромагнитного поля хоть и является весьма значимым в теории, но фундаментальным не является и общностью, такой как уравнение (1) не обладает.

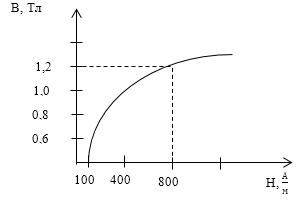
Задание: Определите индукцию магнитного поля (B) и намагниченность (J) сердечника тороида, который имеет N=151 виток. Средний радиус тороида R=3 см. Сила тока в тороиде I=1 А. Используйте график зависимости В(H) рис.1.

За основу решения задачи примем формулу, определяющую напряженность магнитного поля в тороиде:

где $n$ — число витков тороида на единицу длины. Найдем эту величину как:

Тогда выражение (1.1) примет вид:

Для того, чтобы далее воспользоваться графиком (рис.1) проведем вычисление напряженности поля:

Используя график получим, что при $H=800\frac<А><м>$ индукция магнитного поля В=1,2Тл.

Зная материальное уравнение для векторов магнитного поля, в применении к нашему случаю запишем его, как:

из уравнения (1.4) выразим магнитную проницаемость вещества:

Намагниченность связана с напряжением магнитного поля формулой:

\[J=\varkappa H=\left(\mu -1\right)H\left(1.6\right),\]

где $\varkappa $ магнитная восприимчивость. Используя (1.5), получим, что:

Вычислим магнитную проницаемость вещества:

Проведем вычисление намагниченности:

\[J=(1,19\cdot <10>^3-1)\cdot 800\approx 952\cdot 10^3(\frac<А><м>).\]

Ответ: В=1,2Тл, $J=952\cdot 10^3\frac<А><м>.$

Задание: Бесконечно длины соленоид находится в диамагнитной среде, длина соленоида равна l, площадь поперечного сечения S, число витков N. Индуктивность соленоида L, сила тока в нем I. Найдите намагниченность внутри соленоида и его магнитную индукцию.

Зная материальное уравнение, которое связывает напряжённость магнитного поля и индукцию для нашего соленоида:

напряжённость поля длинного соленоида:

и формулу для индуктивности соленоида:

найдем индукцию магнитного поля соленоида. Для этого выразим из (2.3) магнитную проницаемость среды, подставим ее в уравнение (2.1), так же подставим в (2.1) напряженность из (2.2), получим:

Вектор намагниченности связан с вектором напряженности, в нашем случае можно записать, что:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 11 02 2022

Уравнения Максвелла для электромагнитного поля — основные законы электродинамики

Система уравнений Максвелла обязана своим названием и появлением Джеймсу Клерку Максвеллу, сформулировавшему и записавшему данные уравнения в конце 19 века.

Максвелл Джемс Кларк (1831 — 1879) был известным британским физиком и математиком, профессором Кембриджского университета в Англии.

Он практически объединил в своих уравнениях все накопленные к тому времени экспериментально полученные результаты касательно электричества и магнетизма и придал законам электромагнетизма четкую математическую форму. Основные законы электродинамики (уравнения Максвелла) были сформулированы в 1873 году.

Максвелл развил учение Фарадея об электромагнитном поле в стройную математическую теорию, из которой вытекала возможность волнового распространения электромагнитных процессов. При этом оказалось, что скорость распространения электромагнитных процессов равна скорости света (величина которой была уже известна из опытов).

Это совпадение послужило для Максвелла основанием к тому, чтобы высказать идею об общей природе электромагнитных и световых явлений, т.е. об электромагнитной природе света.

Созданная Джеймсом Максвеллом теория электромагнитных явлений нашла первое подтверждение в опытах Герца, впервые получившего электромагнитные волны.

В итоге эти уравнения сыграли главную роль в формировании точных представлений классической электродинамики. Уравнения Максвелла могут быть записаны в дифференциальной или интегральной форме. Практически они описывают сухим языком математики электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и в сплошных средах. К данным уравнениям можно добавить выражение для силы Лоренца, в этом случае мы получим полную систему уравнений классической электродинамики.

Чтобы понимать некоторые математические символы, использующиеся в дифференциальных формах уравнений Максвелла, для начала определим такую занятную вещь, как оператор набла.

Оператор набла (или оператор Гамильтона) — это векторный дифференциальный оператор, компоненты которого являются частными производными по координатам. Для нашего реального пространства, которое является трехмерным, адекватна прямоугольная система координат, для которой оператор набла определяется следующим образом:

где i, j и k – единичные координатные векторы

Оператор набла, будучи применен к полю тем или иным математическим образом, дает три возможные комбинации. Данные комбинации именуются:

Градиент — вектор, своим направлением указывающий направление наибольшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный скорости роста этой величины в этом направлении.

Дивергенция (расхождение) — дифференциальный оператор, отображающий векторное поле на скалярное (то есть, в результате применения к векторному полю операции дифференцирования получается скалярное поле), который определяет (для каждой точки), «насколько расходится входящее и исходящее из малой окрестности данной точки поле», точнее, насколько расходятся входящий и исходящий потоки.

Ротор (вихрь, ротация) — векторный дифференциальный оператор над векторным полем.

Теперь рассмотрим непосредственно уравнения Максвелла в интегральной (слева) и дифференциальной (справа) формах, содержащие в себе основные законы электрического и магнитного полей, включая электромагнитную индукцию.

Интегральная форма: циркуляция вектора напряженности электрического поля по произвольному замкнутому контуру прямо пропорциональна скорости изменения магнитного потока через площадь, ограниченную этим контуром.

Дифференциальная форма: при всяком изменении магнитного поля возникает вихревое электрическое поле, пропорциональное скорости изменения индукции магнитного поля.

Физический смысл: всякое изменение магнитного поля во времени вызывает появление вихревого электрического поля.

Интегральная форма: поток индукции магнитного поля через произвольную замкнутую поверхность равен нулю. Это означает, что в природе нет магнитных зарядов.

Дифференциальная форма: поток силовых линий индукции магнитного поля из бесконечного элементарного объёма равен нулю, так как поле вихревое.

Физический смысл: источники магнитного поля в виде магнитных зарядов в природе отсутствуют.

Интегральная форма: циркуляция вектора напряженности магнитного поля по произвольному замкнутому контуру прямо пропорциональна суммарному току, пересекающему поверхность, охватываемую этим контуром.

Дифференциальная форма: вокруг любого проводника с током и вокруг любого переменного электрического поля существует вихревое магнитное поле.

Физический смысл: протекание тока проводимости по проводникам и изменения электрического поля во времени приводят к появлению вихревого магнитного поля.

Интегральная форма: поток вектора электростатической индукции через произвольную замкнутую поверхность, охватывающую заряды, прямо пропорционален суммарному заряду, расположенному внутри этой поверхности.

Дифференциальная форма: поток вектора индукции электростатического поля из бесконечного элементарного объема прямо пропорционален суммарному заряду, находящемуся в этом объёме.

Физический смысл: источником электрического поля является электрический заряд.

Система данных уравнений может быть дополнена системой так называемых материальных уравнений, которые характеризуют свойства заполняющей пространство материальной среды: