Материальное уравнение электрического поля в диэлектрике

Материальное уравнение для векторов электрического поля

Вы будете перенаправлены на Автор24

Теорема Остроградского — Гаусса

Одним из фундаментальных уравнений электростатики является теорема Остроградского — Гаусса:

«Поток вектора электрического смещения ($Ф_D$) (электрической индукции) через замкнутую поверхность равен сумме свободных зарядов ($q_i$), которые находятся внутри этой поверхности)».

Математическая форма записи интегральной форме этой теоремы для электрического поля в диэлектрике выглядит следующим образом (система СИ):

где $D_n$ — нормальная составляющая вектора электрического смещения, $dS$ — элемент поверхности, через которую ищется поток вектора $\overrightarrow$.

В дифференциальном виде эта же теорема выглядит следующим образом:

где $\rho $ — объемная плотность свободных зарядов. Выражения (1) и (2) справедливы не только в электростатике, они выполняются и для переменных полей. Уравнения (1) и (2) являются составной частью системы фундаментальных уравнений Максвелла для электродинамики.

В вакууме поле можно охарактеризовать одним вектором напряженности уравнения (1) или (2) записываются для него и их достаточно. В таком случае, если к ним добавляется теорема о циркуляции вектора напряженности:

где $\overrightarrow$ — вектор напряженности электрического поля, $d\overrightarrow$ — элемент перемещения вдоль контура L. Интеграл в левой части уравнения (3) есть циркуляция вектора напряженности по контуру L. Характерным свойством электростатического поля является то, что циркуляция его вектора напряжённости по любому замкнутому контуру равна нулю.

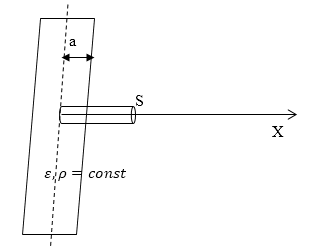
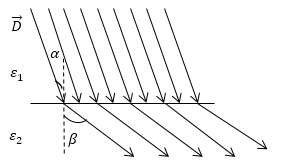
В вакууме уравнения (1 или 2) и (3) образуют полную систему уравнений электростатики. В веществе этих уравнений не достаточно, так как необходимо описать поведение самой среды в электрическом поле. Следовательно, к выше названным уравнениям электростатики добавляют еще одно векторное уравнение, которое называют материальным уравнением. Оно связывает вектор напряженности поля ($\overrightarrow$) и вектор электрического смещения ($\overrightarrow$) или вектор напряженности поля и вектор поляризации ($\overrightarrow

$).

В основном, способ получения такого уравнения содержится уже в определении $\overrightarrow

$. Так как если нам известна атомная структура вещества, то можно рассчитать, как смещаются электроны и атомные ядра под воздействием электрического поля. Значит, можно вычислить вектор поляризации и таким образом получить нужное нам уравнение. Однако если идти данным путем, то в зависимости от конкретных условий могут получаться весьма разные соотношения, что неудобно.

Опыты показали, что для большого класса диэлектриков и широкого круга явлений связь между векторами поляризации ($\overrightarrow

$) и напряженности ($\overrightarrow$) линейна и однородна, то есть:

\[\overrightarrow

=\varkappa <\varepsilon >_0\overrightarrow\ \left(4\right),\]

где $\varkappa $ — диэлектрическая восприимчивость (безразмерная величина), уравнение записано в системе СИ. Такая связь между векторами $\overrightarrow

$ и $\overrightarrow$ объясняется тем, что напряженности макроскопических полей невелики в сравнении с напряженностями внутри молекул и атомов. Уравнение выполняется, если диэлектрик изотропен. В таком случае векторы напряженности и поляризуемости коллинеарные. Коэффициент $\varkappa \ $зависит от плотности диэлектрика и температуры.

В анизотропных диэлектриках направление вектора напряженности и вектора поляризации не совпадают. И их связь устанавливается в виде:

где индексы i,j — нумеруют компоненты по осям декартовой системы координат ($i=x,\ y,z;j=x,\ y,z$), $<\varkappa >_$ — тензор диэлектрической восприимчивости.

По определению, вектор $\overrightarrow\$ равен:

Следовательно, для изотропного диэлектрика используем (4), запишем:

\[\overrightarrow=<\varepsilon >_0\overrightarrow+\varkappa <\varepsilon >_0\overrightarrow=\left(1+\varkappa \right)<\varepsilon >_0\overrightarrow=\varepsilon <\varepsilon >_0\overrightarrow\left(7\right),\]

Материальные уравнения для векторов электрического поля

\[\overrightarrow=\varepsilon <\varepsilon >_0\overrightarrow,\] \[\overrightarrow

=\varkappa <\varepsilon >_0\overrightarrow\ \left(8\right).\]

называют материальными уравнениями для векторов электрического поля.

Эти соотношения, несмотря на их значимость, являются приближенными и не относятся к фундаментальным, так как область применения их ограничена. Существуют вещества, к которым уравнения (8) не применимы. Например, ионные кристаллы могут быть поляризованы в отсутствии внешнего поля. Поведение же, например, электретов (веществ, которые длительное время сохраняют состояние поляризации в отсутствии электрического поля) можно охарактеризовать вектором поляризации, который с вектором напряженности связан уравнением:

где $\overrightarrow$ и $\varkappa $ не зависят от напряженности поля.

Задание: Бесконечная пластина из однородного, изотропного диэлектрика с диэлектрической проницаемостью$\ \varepsilon $ заряжена равномерно сторонними зарядами, объемная плотность распределения этого заряда равна $\rho $. Толщина пластины 2а. Найдите поляризованность диэлектрика как функцию х (рис.1). Вне пластины диэлектрическую проницаемость среды считать равной единице.

Для бесконечной пластины диэлектрика напряженность поля зависит от одной координаты (в нашем случае — x). Допустим, что ось X направлена перпендикулярно к плоскости пластины и ее начало совпадает с центром слоя диэлектрика. Напряженность бесконечной пластины легко находится из теоремы Остроградского — Гаусса. Выберем в качестве поверхности, поток через которую будем искать прямой цилиндр, ось которого параллельна оси X (рис.1)площадь основания равна $S$. В таком случае поток вектора напряженности для точек внутри пластины ($\ при\ |x| \[Ф_E=E\cdot S=\frac<\varepsilon <\varepsilon >_0>=\frac<\rho Sx><\varepsilon <\varepsilon >_0>\ \left(1.1\right),\]

где x — высота цилиндра для внутренности пластины она изменяется от $-a

напряженность поля равна:

Силовые линии, создаваемые полем пластины, направлены вдоль оси X.

Зная, что диэлектрик изотропный, используем связь напряженности и вектора поляризации, учитываем, что вне плоскости связанных зарядов нет:

\[\overrightarrow

=\varkappa <\varepsilon >_0\overrightarrow\ \left(1.5\right).\]

Найдем модуль вектора поляризации:

где $\varepsilon =1+\varkappa ,\ \to \varkappa =\varepsilon -1$. По направлению вектор поляризации будет совпадать с вектором напряженности.

Готовые работы на аналогичную тему

Задание: На рис. 2 изображена картина линий вектора $\overrightarrow\ $при переходе их одного диэлектрика ($<\varepsilon >_1$) в другой $(<\varepsilon >_2)$. Какая из диэлектрических проницаемостей среды больше?

Рассмотрим, как ведут себя силовые линии при прохождении через границу раздела двух диэлектриков. В том случае, если на границе нет свободных зарядов, то должны выполняться граничные условия:

Для тангенциальной составляющей напряженности поля:

и нормальной составляющей:

Если использовать функции углов, которые показаны на рис. 1, то получим:

\[E_1sin\alpha =E_2sin\beta \ \left(2.3\right).\] \[<<\varepsilon >_1E>_1cos\alpha =<\varepsilon >_2E_2cos\beta \left(2.4\right).\]

Зная связь между напряженностью и вектором смещения для изотропного диэлектрика:

\[\overrightarrow=\varepsilon <\varepsilon >_0\overrightarrow\ \left(2.5\right),\]

Разделим (2.6) на (2.7), получим:

Из уравнения (2.8) видно, что при переходе через границу из диэлектрика с меньшей диэлектрической проницаемостью в диэлектрик с большей проницаемостью угол увеличивается, то есть силовая линия удаляется от нормали. Значит, для нашего случая $<\varepsilon >_2><\varepsilon >_1$.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 04 12 2021

Курс I. Уравнения Максвелла в диэлектрической среде

Уравнения Максвелла в диэлектрической среде

Уравнения Максвелла в произвольной среде таковы

(1a)

система (1a) замыкается материальными соотношениями . Здесь — векторы электрической и магнитной индукции; — плотность токов проводимости; — плотность электрических зарядов; — величины, характеризующие свойства среды и считающиеся при этом заданными функциями точки, но не времени; — сторонние электродвижущие силы – заданные функции точки и времени.

Заметим, что в приведенном, общепринятом виде (1a) формулировка уравнений принадлежит Герцу (Максвелл уравнения приводил в интегральной форме).

Заметим также, что система (1a) – это постулат, обобщающий все известные до Максвелла явления электричества и магнетизма (Кулон 1785 г. – закон взаимодействия электрических зарядов; Эрстед 1820 г. – магнитное действие тока, существование связи между магнитными и электрическими явлениями; Ампер – все магнитные явления в природе вызваны электрическими токами (теория молекулярных токов Ампера); Фарадей 1831 г. – электромагнитная индукция; и т. д.)

Волновое уравнение. Электромагнитная природа света.

Для интересующих нас в дальнейшем диэлектриков с , система Максвелла принимает вид

(1.1)

.

откуда, если диэлектрическая проницаемость не зависит от времени, получаем

(1.2)

Из векторного анализа известно

,

тогда (1.2) принимает вид

(1.3)

Далее, из условия находим

, (1.4)

В результате, вместо (1.3) имеем

(1.5)

Аналогично, для найдем

(1.6)

В случае однородных диэлектриков , и (1.5),(1.6) принимают вид

(1.7)

Уравнения (1.7) называются волновыми. Их справедливость ограничена лишь требованием однородности среды и отсутствия в ней токов проводимости и свободных зарядов.

К ним относятся как граничные условия на поверхностях разделов сред, так и условия на границах рассматриваемой области пространства. Последние полностью определяются конкретными условиями задачи (например, условия на бесконечности).

Условия на границах разделов для диэлектриков (отсутствие поверхностных зарядов и токов проводимости) эквивалентны уравнениям

, , (1.8)

где индексы 1 и 2 относятся к двум граничащим средам, а t означает любое направление, касательное к поверхности раздела.

Плоские электромагнитные волны

Одним из простейших решений волнового уравнения является плоская волна.

Волна называется плоской, если в любой момент времени во всех точках произвольной плоскости, перпендикулярной направлению распространения волны, векторы поля постоянны. Если этим направлением считать ось z, то компоненты поля плоской, монохроматической волны имеют вид

, , (1.9)

где — частота; векторы , вообще говоря, комплексные и зависят только от координаты z.

Подстановка (1.9) в волновые уравнения (1.7) дает

, , (1.10)

где — волновое число в диэлектрике.

Элементарно решив (1.10), найдем решения волновых уравнений в случае плоских волн в виде

, , (1.11)

каждое из которых представляет собой суперпозицию двух волн, распространяющихся в противоположных направлениях оси z. Здесь — произвольные постоянные интегрирования.

Обычно, в качестве решения рассматривается одна из волн, например,

, . (1.12)

С помощью найденного простейшего решения (1.12) можно продемонстрировать ряд важнейших общих свойств электромагнитных волн.

В частности, если ось z координатной системы не совпадает с направлением распространения волны, дифференцирование векторов поля по координатам сведется к их умножению на величину , где — единичный вектор в направлении распространения. Для однородных диэлектриков из уравнений Максвелла имеем

, , (1.13)

откуда следует, что векторы и перпендикулярны к , т. е. плоские электромагнитные волны – суть поперечные волны.

По аналогии, дифференцирование векторов поля по t сводится к их умножению на . В частности, из второго уравнения Максвелла (1.1) получаем

,

или, с учетом ,

. (1.14)

Последнее означает, что векторы и взаимно перпендикулярны, а три взаимно перпендикулярных вектора , и образуют правовинтовую систему.

Из (1.14) следует также, что , т. е. отношение числовых значений векторов и от времени не зависит, т. е. эти векторы обладают одинаковыми фазами и изменяются синхронно.

Всегда следует помнить, что физический смысл компонент поля, записанных в комплексной форме (см., например, запись (1.12)), несут лишь действительные части этих выражений. При этом каждая из декартовых компонент электрического и магнитного векторов поля плоской, монохроматической волны имеет вид

a>0. (1.15)

Здесь обозначает переменную часть фазового множителя, т. е.

, (1.16)

— направление распространения волны; — постоянная часть этого множителя.

Совместим ось z c . Тогда, в силу поперечности волны отличными от нуля будут только x — и y-компоненты векторов. Исследуем характер кривой, которую конец электрического (или магнитного) вектора описывает в произвольной точке пространства. Эта кривая – геометрическое место точек с координатами

(1.17)

a) Эллиптическая поляризация

После несложных математических операций исключим из (1.17) и получим

, (1.18)

где .

В аналитической геометрии показывается, что (1.18) представляет собой уравнение конического сечения, а более конкретно – уравнение эллипса. Этот эллипс вписан в прямоугольник, стороны которого параллельны координатным осям и имеют длины и . Таким образом, конец электрического вектора описывает эллипс в любой плоскости, перпендикулярной направлению распространения.

Аналогично показывается, что конец магнитного вектора поля также описывает эллипс, вписанный в прямоугольник со сторонами в раз большими. Последнее следует, в частности, из соотношения (1.14).

Из общих физических соображений следует также различать две возможные эллиптические поляризации в соответствии с направлением, в котором конец электрического вектора описывает эллипс. В литературе сформировалось определение, согласно которому правой поляризация называется, когда наблюдателю, смотрящему навстречу световому лучу, кажется, что конец электрического вектора движется по часовой стрелке. Для левой эллиптической поляризации справедливо обратное.

Поскольку параметры в предыдущем рассмотрении были произвольными, то эллиптическую поляризацию электромагнитных волн следует считать наиболее общим из состояний поляризации. Более частные типы поляризации соответствуют определенным соотношениям между этими параметрами.

b) Линейная и круговая поляризации

Перейдем к рассмотрению частных случаев.

,

то эллипс (1.18) превратится в прямую линию. В самом деле, уравнение (1.18) переходит при этом в

, (1.19)

а конец электрического вектора в прямоугольнике колеблется вдоль одной из его диагоналей.

Иногда эта линейная поляризация называется еще плоской поляризацией. Понятно, что в этой ситуации магнитный вектор также линейно поляризован.

Другим частным случаем эллиптической поляризации является круговая. Переход от эллиптической к круговой поляризации происходит тогда, когда, во-первых, и, во-вторых,

, .

Уравнение (1.18) переходит при этом в уравнение окружности

, (1.20)

где также различают правую и левую поляризации.

Круговая поляризация иногда называется циркулярной.

Итак, во всех случаях поляризованного света концы векторов поля в каждой точке движутся периодически. В случае же неполяризованного света они движутся совершенно нерегулярно, и такие световые колебания не имеют никаких преимущественных направлений в плоскости, перпендикулярной направлению распространения.

Основные законы оптики – преломление света, отражение, полное внутреннее

Применим теперь найденные выше для плоских волн соотношения к исследованию распространения этих волн при наличии плоской границы, разделяющей два однородных, изотропных диэлектрика, занимающих два полупространства.

В задаче о преломлении волн на границе полубесконечной среды физический смысл имеет решение, основанное на предположении о наличии трех волн: падающей, отраженной и преломленной.

Падающая на границу волна порождает новый волновой процесс.

По определению плоская волна полностью определена, если известно ее поведение во времени в некоторой точке пространства. Вторичные поля, возникающие на границе, будут так же изменяться во времени, как и первичное поле падающей волны. Поэтому переменные части фазовых множителей трех волн в произвольной точке должны быть одинаковыми:

, (1.21)

где — единичные векторы в направлениях падающей, отраженной и преломленной волн; — скорости распростра

нения волн в обеих средах.

Выбрав в качестве границы раздела плоскость z=0, (1.21) запишем в виде

. (1.22)

Равенства должны выполняться для любых значений x и y на границе. Это дает

(1.23)

откуда следует, что все три вектора лежат в одной плоскости с нормалью к границе (в плоскости падения).

Выберем в качестве плоскости падения плоскость xz. Тогда y-компоненты векторов равны нулю, а прочие таковы:

(1.24)

где — углы, которые образуют с осью z (рис. 1).

Из (1.24) и (1.23) имеем

(1.25)

откуда , и из рис. 1 видно, что , т. е. угол падения равен углу отражения. В этом состоит закон отражения.

Из (1.25) следует также

(1.26)

Последнее соотношение вместе с утверждением, что нормаль к преломленной волне лежит в плоскости падения составляет закон преломления (или закон Снеллиуса).

Если > (луч падает из более плотной в менее оптически плотную среду), то из (1.26) видно, что для любого угла падения существует вещественный угол преломления ( воспользуемся им и положим

Тогда (1.27) примет вид

(1.28)

Ясно также, что физический смысл имеет лишь нижний знак перед корнем во втором сомножителе в (1.28).

Из (1.28) следует, и это подтверждается опытным путем, что электромагнитное поле в среде 2 все же не равно нулю. Волна (1.28) представляет собой неоднородную волну, распространяющуюся в плоскости падения вдоль x по поверхности раздела сред и с экспоненциально падающей с ростом z амплитудой. Эта волна не является поперечной, поскольку ее компонента электрического вектора . Эффективная глубина ее проникновения в обе стороны от поверхности раздела сред оказывается порядка длины волны.

1. . Электромагнитные волны. Сов. Радио, 1957.

2. М. Борн, Э. Вольф. Основы оптики. М., Наука, 1970.

3. . Основы теории электричества. М., Наука, 1989.