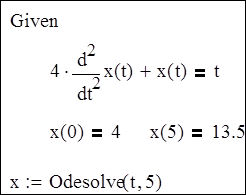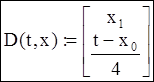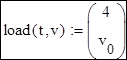Mathcad дифференциальные уравнения второго порядка
При решении дифференциального уравнения искомой величиной является функция. Для ОДУ неизвестная функция — функция одной переменной. Дифференциальные уравнения в частных производных — это дифференциальные уравнения, в которых неизвестной является функция двух или большего числа переменных. Mathcad имеет ряд встроенных функций, предназначенных для решения ОДУ. Каждая из этих функций предназначена для численного решения дифференциального уравнения. В результате решения получается матрица, содержащая значения функции, вычисленные на некотором множестве точек (на некоторой сетке значений). Для каждого алгоритма, который используется при решении дифференциальных уравнений, Mathcad имеет различные встроенные функции. Несмотря на различные методы поиска решения, каждая из этих функций требует, чтобы были заданы по крайней мере следующие величины, необходимые для поиска решения:
- Начальные условия.
- Набор точек, в которых нужно найти решение.
- Само дифференциальное уравнение, записанное в некотором специальном виде, который будет детально описан в этой главе.
В этом разделе описано, как решить ОДУ, используя функцию rkfixed. Раздел начинается с примера того, как решить простейшее дифференциальное уравнение первого порядка. Затем будет показано, как можно решать дифференциальные уравнения более высокого порядка.
Дифференциальные уравнения первого порядка
Дифференциальное уравнение первого порядка — это уравнение, которое не содержит производных выше первого порядка от неизвестной функции. На Рисунке 1 показан пример того, как решить относительно простое дифференциальное уравнение:
с начальными условиями: y(0) = 4
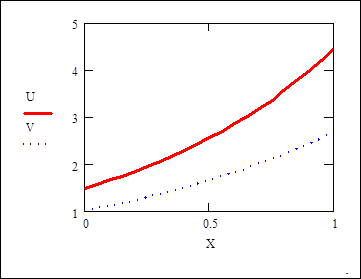
Функция rkfixed на Рисунке 1 использует для поиска решения метод Рунге-Кутты четвертого порядка. В результате решения получается матрица, имеющая два следующих столбца:
- Первый столбец содержит точки, в которых ищется решение дифференциального уравнения.
- Второй столбец содержит значения найденного решения в соответствующих точках.
Рисунок 1: Решение дифференциального уравнения первого порядка.
Функция rkfixed имеет следующие аргументы:
| y = | Вектор начальных условий размерности n, где n — порядок дифференциального уравнения или число уравнений в системе (если решается система уравнений). Для дифференциального уравнения первого порядка, как, например, для уравнения, приведенного на Рисунке 1, вектор начальных значений вырождается в одну точку y0 = y(x1). |
| x1, x2 = | Граничные точки интервала, на котором ищется решение дифференциальных уравнений. Начальные условия, заданные в векторе y, — это значение решения в точке x1. |
| npoints = | Число точек (не считая начальной точки), в которых ищется приближенное решение. При помощи этого аргумента определяется число строк (1 + npoints) в матрице, возвращаемой функцией rkfixed. |
| D (x, y) = | Функция, возвращающая значение в виде вектора из n элементов, содержащих первые производные неизвестных функций. |
Наиболее трудная часть решения дифференциального уравнения состоит в определении функции D(x, y), которая содержит вектор первых производных от неизвестных функций. В примере, приведенном на Рисунке 1, было достаточно просто разрешить уравнение относительно первой производной , и определить функцию D(x, y). Иногда, особенно в случае нелинейных дифференциальных уравнений, это может быть трудно. В таких случаях иногда удаётся разрешить уравнение относительно в символьном виде и подставить это решение в определение для функции D(x, y). Используйте для этого команду Решить относительно переменной из меню Символика.
Рисунок 2: Более сложный пример, содержащий нелинейное дифференциальное уравнение.
Дифференциальные уравнения второго порядка
Как только Вы научились решать дифференциальное уравнение первого порядка, можно приступать к решению дифференциальных уравнений более высокого порядка. Мы начнем с дифференциального уравнения второго порядка. Основные отличия от уравнения первого порядка состоят в следующем:
- Вектор начальных условий y теперь состоит из двух элементов: значений функции и её первой производной в начальной точке интервала x1.
- Функция D(t, y) является теперь вектором с двумя элементами:
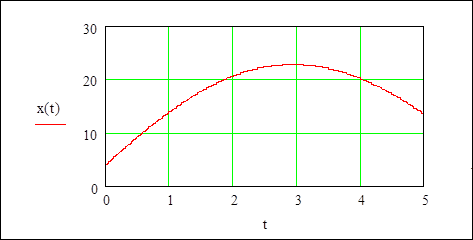
Пример, приведенный на Рисунке 3, показывает, как решить следующее дифференциальное уравнение второго порядка:
Рисунок 3: Решение дифференциального уравнения второго порядка.
Уравнения более высокого порядка
Методика решения дифференциальных уравнений более высокого порядка является развитием методики, которая применялась для решения дифференциальных уравнений второго порядка. Основное различие состоит в следующем:
- Вектор начальных значений y теперь состоит из n элементов, определяющих начальные условия для искомой функции и ее производных y, y’ , y». y (n-1)
- Функция D является теперь вектором, содержащим n элементов:
Пример, приведенный на Рисунке 4, показывает, как решить следующее дифференциальное уравнение четвертого порядка:
с начальными условиями:
Рисунок 4: Решение дифференциального уравнения более высокого порядка.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Mathcad дифференциальные уравнения второго порядка
Электронный курс по MathCAD



5.2 Решение дифференциальных уравнений и систем.(Задача Коши и граничные задачи).
Решение одиночного дифференциального уравнения.
Для численного решения одиночного дифференциального уравнения в MathCAD имеется функция Odesolve, с помощью которой может быть решена как задача Коши для обыкновенного дифференциального уравнения, так и граничная задача. Эта функция входит в состав блока решения и сявляется его заключительным ключевым словом.
Odesolve(x,b,[step]) — Возвращает функцию, которая является решением дифференциального уравнения. Используется в блоке с оператором Given.
x — переменная интегрирования, действительное число
b — конечная точка отрезка интегрирования
step — величина шага по переменной интегрирования (необязательный аргумент)
Замечания:
- Уравнение должно быть линейным относительно старшей производной.
- Число заданных начальных или граничных условий внутри блока должно быть равно порядку уравнения.
- При записи уравнения для обозначения производных функции используйте специальные кнопки с панели Math или ‘ (штрих) — [Ctrl+F7], для знака равенства = [Ctrl+=] (в том числе и для дополнительных условий).
- Конечная точка должна быть больше начальной.
- Не допускаются начальные и граничные условия смешанного типа (f ‘(a)+f(a)=5).
- Искомая функция в блоке дложна быть обязательно с аргументом ( f(x))
 |  |
Численное решение задачи Коши для дифференциальных уравнений и систем.
Для численного решения задачи Коши для дифференциальных уравнений и систем могут быть использованы функции:
rkfixed(y,x1,x2,n,F) — возвращает матрицу решений системы уравнений методом Рунге-Кутта 4-го порядка при фиксированном шаге по x
rkadapt(y,x1,x2,n,F) — ищет решение с переменным шагом ( там, где решение меняется медленнее, шаг увеличивается, а в области быстрого изменения решения шаг функции уменьшается). Возвращается решение с равным шагом. Функция работает быстрее, чем rkfixed
Bulstoer(y,x1,x2,n,F) — дает более точное решение (методом Bulirsch-Stoer)
Агрумкнты вышеуказанных функций:
y — вектор начальных условий
x1,x2 — границы интервала для поиска решения
n — количество точек на интервале
F(x,y) — вектор-функция первых производных
При решении дифференциальных уравнений порядка выше первого (или систем уравнений, выше первого порядка) исходное уравнение (систему) необходимо преобразовать к системе дифференциальных уравнений первого порядка.
В результате работы укзанных функций рассчитывается матрица, количество стобцов которой равно порядку уравнения +1(или сумме порядков уравнений в системе +1), а количество строк равно параметру n. Первый столбец содержит значения независимой переменной, второй — значение функции, третий — для диф. уравнений 2-го порядка — значение производной искомой функции (если решается система двух уравнений 1-го порядка, то третий столбец будет содержать значения второй функции). Для выделения решений (функций или их производных) можно воспользоваться стандартным оператором вывода столбцов матрицы M < >
Если матрица правых частей дифференциальных уравнений почти вырождена, то такие системы называются жесткими. В этом случае решения, возвращаемые функцией rkfixed будет неустойчивым и для решения таких систем необходимо применять функции Stiffb , Stiffr
Stiffb(y,x1,x2,n,F,J) — ищет решение диф. уравнения или системы дифференциальных уравнений методом Bulirsch-Stoer
Stiffr(y,x1,x2,n,F,J) — ищет решение диф. уравнения или системы дифференциальных уравнений методом Rosenbrock
 |
 |
 |
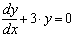
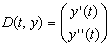

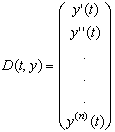










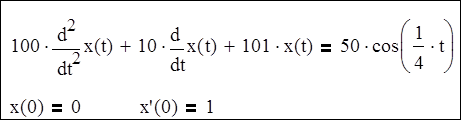
 Набрать слово Given
Набрать слово Given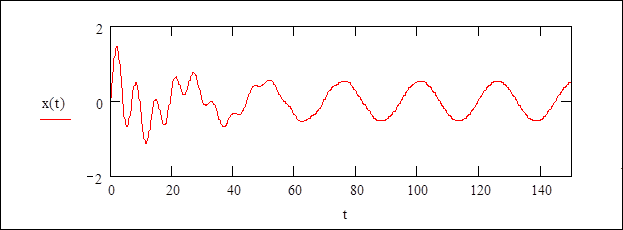
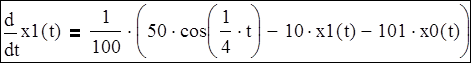
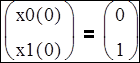
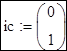
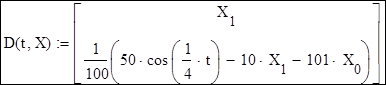
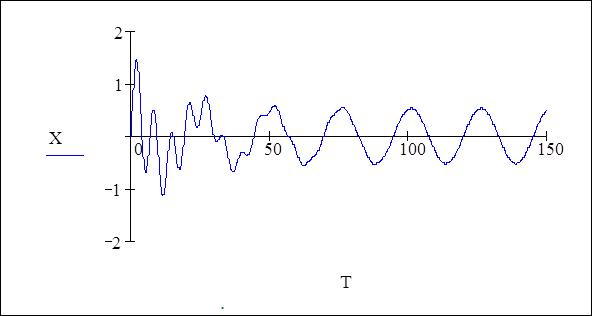

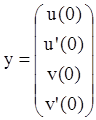 , т.е. указать
, т.е. указать 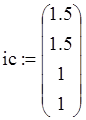
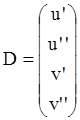 , т.е.
, т.е. 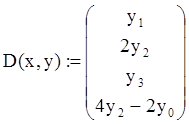
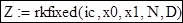 ,
,