Mathcad решить аналитически систему уравнений

Решение систем уравнений в MathCad

Для решения уравнений в Mathcad можно воспользоваться двумя способами. Эти способы были частично рассмотрены в разделе «Решение уравнений»:

Использование метода Given — Find:

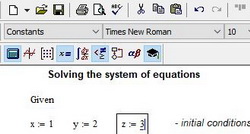
В рабочем поле mathcad записываем слово Given. Это служебное слово. Оно подключает определенные программные модули mathcad для обработки исходных данных, необходимых для решения системы уравнений численными методами.

Затем указывается начальное приближение для искомых переменных. Это нужно для увеличения скорости и точности решения системы. Если начальное приближение не задать, то mathcad по умолчанию примет его равным нулю для всех переменных, при этом, если окажется, что система имеет несколько решений, то есть риск не определить все корни. Поэтому лучше всегда задавать приближение

Рис. 1. Ввод исходных данных в поле mathcad

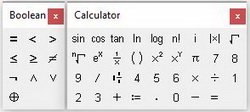
Далее вводятся уравнения. Их можно записать в явном или неявном виде. Само уравнение набирается с клавиатуры вручную с использованием панели Calculator. Из этой панели можно взять основные математические операции: дроби, тригонометрию, факториалы и прочее. Уравнение нужно записывать с использованием логического символа «ровно». На панели Boolean он выделен жирным шрифтом (см. рис. 2)

Рис. 2. Панели Boolean и Calculator

Когда уравнения записаны вводится функция Find(x, y, z. ) (где х, y, z. — переменные). Это функция, которая возвращает результат решения системы. Значение функции Find() можно присвоить какой-либо переменной с помощью символа «:=» и использовать ее далее в расчетах (см. рис. 3). При решении систем уравнений в mathcad результатом всегда будет являтся матрица значений

Рис. 3. Ввод функции Find()

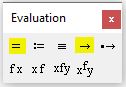
Для того чтобы увидеть результат решения системы уравнений, после Find(x, y, z. ) следует поставить символ «→» либо «=» из панели Evaluation (см. рис. 4).

Рис. 4. Панель «Evaluation»

В зависимости от сложности системы через определенное время MathCad выведет результат. На рис. 5 можно рассмотреть синтаксис и результат решения системы уравнений. Обратите внимание, что можно присваивать результат решения системы матричной переменной и можно работать с отдельными ее элементами

Рис. 5. Результат численного решения системы уравнений

Mathcad позволяет решать системы уравний в символьном виде. Обычно это полезно, когда требуется получить не точное значение переменных, а их выражения через константы. Например, если мы заменим все числовые константы на неизвестные параметры и решим уравнение относительно x, y и z, то результат выведется в символьном виде (см. рис. 6). Причем, обратите внимание, что в данном случае нам не нужно вводить начальное приближение и мы должны использовать символ «→» для вывода результата. Как правило, символьное решение получается громоздким, поэтому не всегда рекомендуется использовать этот метод

Рис. 6. Результат символьного решения системы уравнений

Использование метода Solve:

Как показывает практика, методом solve иногда удается решить системы уравнений, которые не поддаются решению с помощью функции Find()

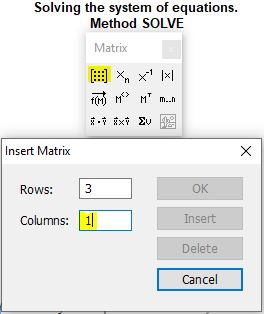
Синтаксис следующий: на панели matrix нажимаем иконку Matrix or Vector и в появившемся окне указываем количество уравнений входящих в систему. В нашем примере их будет три (см. рис. 7)

Рис. 7. Создание матрицы для метода SOLVE

Заполняем систему, вводя последовательно все уравнения используя логический символ «ровно» из панели Boolean. Каждый элемент матрицы-столбца содержит одно уравнение (см. рис. 8)

Рис. 8. Ввод системы уравнений для метода SOLVE

Когда все уравнения введены, убедитесь, что курсор ввода находится в вашей матрице и затем нажмите кнопку «solve» из панели Symbolic. Появится служебное слово (функция) solve. Далее поставте запятую и введите последовательно все переменные, относительно которых необходимо решить систему уравнений (см. рис. 9)

Рис. 9. Синтаксис метода SOLVE для решения систем

Уведите курсор в свободное поле mathcad и дождитесь окончания решения системы. Обратите внимание, что мы не вводили начальные приближения. Даный метод их назначает автоматически. Обратите так же внимание, что для решения системы в символьном виде синтаксис аналогичен (см. рис. 10)

Рис. 10. Синтаксис метода SOLVE для решения систем

Как показывает моя инженерная практика, решение систем в символьном виде сопряжено с большими вычислительными трудностями. То есть иногда решение системы занимает массу времени, и в итоге mathcad выдает выражение для одной переменной непомерной длины, которое нельзя использовать. Поэтому рекомендуется прменять эту возможность лишь в крайних случаях и по возможности «помогать» mathcad, заменяя константы известными числовыми значениями

Donec eget ex magna. Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fergiat. Pellentesque in mi eu massa lacinia malesuada et a elit. Donec urna ex, lacinia in purus ac, pretium pulvinar mauris. Curabitur sapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique.

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Duis dapibus rutrum facilisis. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam tristique libero eu nibh porttitor fermentum. Nullam venenatis erat id vehicula viverra. Nunc ultrices eros ut ultricies condimentum. Mauris risus lacus, blandit sit amet venenatis non, bibendum vitae dolor. Nunc lorem mauris, fringilla in aliquam at, euismod in lectus. Pellentesque habitant morbi tristique senectus et netus et malesuada fames ac turpis egestas. In non lorem sit amet elit placerat maximus. Pellentesque aliquam maximus risus, vel venenatis mauris vehicula hendrerit.

Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fersapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique lorem ipsum dolor.

MathCAD — это просто! Часть 5. Системы нелинейных уравнений

Добрый день, уважаемые читатели и читательницы, мы с вами продолжаем грызть гранит науки. Делаем мы это с целью — напомню, если кто вдруг успел позабыть — овладеть замечательным математическим пакетом под названием MathCAD. И в прошлый раз мы с вами закончили на решении систем линейных алгебраических уравнений, для простоты также обозначаемых как СЛАУ. Что ж, линейные уравнения — это, конечно же, спору нет, замечательно. Однако на них, к величайшему сожалению многих поколений школьников и студентов, математические задачи далеко не заканчиваются, а даже, я бы сказал, напротив. То есть СЛАУ — это только частный случай систем уравнений, которые могут в обыкновенной вычислительной практике оказаться совсем даже и не линейными, а, напротив, нелинейными (да, именно так их и называют математики). Системы нелинейных уравнений без использования MathCAD или какого-либо другого математического пакета решать обычно не просто трудно, а очень трудно, но в MathCAD подход к ним не слишком отличается от подхода к СЛАУ — в этом вы сейчас получите возможность убедиться лично.

В общем-то, основные аспекты аналитического решения систем уравнений мы с вами уже, по большому счету, обсудили. Когда это мы так лихо успели? А вот именно тогда, когда обсуждали аналитическое решение систем линейных уравнений с помощью оператора solve. Оказывается, все те же методы вполне применимы для решения систем нелинейных уравнений. Тем не менее, чтобы вы лучше их усвоили, повторю еще раз кратко алгоритм их решения с помощью MathCAD’а и приведу небольшой пример решения подобной системы. Давайте попробуем решить следующую систему уравнений: ex + y + z(xyz)1/2 = 0
(x + y+ z)1/2 = c
x +y + cz = 0

Система выглядит несложной, но для того, чтобы решить ее без использования MathCAD’а, даже очень хорошему математику потребуется не такое уж малое количество времени. Естественно, MathCAD с этой системой справится в два счета. Для ее решения создайте матрицу размером 3 на 1 (3 строки, 1 столбец), в которую и поместите уравнения нашей системы. Напомню, что для того, чтобы MathCAD распознавал уравнения как уравнения, знак «равно» нужно нажимать, удерживая клавишу Ctrl. После того, как система будет введена в виде матрицы, найдите на панели Symbolic оператор solve — мы им уже неоднократно пользовались для решения и простых уравнений, и СЛАУ, так что вы, по идее, уже должны были запомнить, где именно он находится. После оператора через запятые укажите переменные, которые входят в нашу систему уравнений — это пусть будут для начала x, y и z. Поскольку при вводе solve с панели Symbolic MathCAD сам добавляет нужную стрелочку для аналитического решения нашей с вами системы уравнений, то больше ничего, в общем-то, делать не нужно — дальше MathCAD будет решать систему. Сколько это времени у него займет, зависит, конечно же, от мощности вашего компьютера, ну и от самой системы. Нашу систему он решит быстро, а вот если поизвращаться и написать какую-нибудь систему тригонометрических и логарифмических уравнений, да еще и с комплексными переменными (о них мы потом еще поговорим отдельно), то решать такое MathCAD может на слабых компьютерах и не один час.

Для чистоты эксперимента поменяем переменные: пусть теперь произвольной константой в нашей системе будет не c, а z. В этом случае нас ожидает совершенно другое, куда как более громоздкое, решение этой самой системы.

Как видите, аналитическое решение систем нелинейных уравнений с помощью MathCAD’а — вещь несложная, только, к сожалению, возможная далеко не всегда. Как обычно, на помощь символьному процессору MathCAD, который опускает в бессилии руки перед сложными системами, спешат численные методы. Вот здесь уже начинаются различия с системами линейных уравнений.

Численное решение нелинейных систем

В целом алгоритм решения систем нелинейных уравнений в MathCAD для пользователя мало чем отличается от него же для СЛАУ. Мы точно так же задаем начальные приближения, пишем «Given», записываем под этим словом наши уравнения и запрягаем функцию Find, которая должна вывести эти самые уравнения на чистую воду. Все точно так же, как тогда, когда мы решали СЛАУ.

Почему же я так пугал вас буквально двумя абзацами выше, говоря о том, что решать системы нелинейных уравнений намного сложнее, чем СЛАУ? Дело в том, что в случае нелинейных уравнений намного сложнее подобрать такие начальные значения, чтобы численное решение сходилось к реальным значениям корней уравнений. Честно говоря, со СЛАУ тоже не всегда все так просто, как я в прошлый раз сказал, однако в крайнем случае можно заставить MathCAD решить СЛАУ аналитически, а затем просто подставить конкретное численное значение какого-нибудь коэффициента. С нелинейными системами такой прием, что называется, «не покатит». Именно поэтому для получения максимального точного решения многих из таких систем придется озадачиться такими вещами, как задание начальных значений для наших переменных.

Первый способ, который я вам предложу, сразу предупреждаю, для людей неленивых. Заключается он в банальном подборе значений переменных собственными руками. То есть для начала берем начальные значения «с потолка» и решаем систему с помощью Find’а. Подставляем значения, выданные этой функцией, в исходные уравнения и смотрим, насколько они похожи на истинные решения. Если уравнения обращаются при подстановке в верные равенства, то все хорошо: либо система была простой, либо в вас дремлет талант подбирателя корней уравнений. Но если равенством после подстановки и близко не пахнет, то придется попотеть. Нужно начать изменять значения начальных приближений для каждой переменной и смотреть, как это отразится на близости выражений, получившихся после подстановки решений в уравнения, к равенствам. Таким нехитрым методом можно за не столь долгое время, как может сначала показаться, добиться хорошего приближения начальных значений к реальным решениям. И, несмотря на явный садомазохистский характер данного метода, он имеет то неоспоримое преимущество, что действует железно на любые системы и любые переменные — было бы терпение.

Второй метод, который я хочу предложить, этим достоинством не обладает, но зато и не требует от пользователя столь деятельного участия в решении. Думаю, вы сами сможете сформулировать главный его недостаток, если я скажу, что с этим методом мы уже сталкивались, и заключается он в построении графиков для уравнений, входящих в систему. Да, главный недостаток — это сложность в применении к системам уравнений, содержащим более трех переменных. Сложно, сами понимаете, изобразить на мониторе компьютера 25-мерное пространство для отображения решений системы с 25-ю переменными. Но для тех систем, которые содержат две или три переменные, построить график мы вполне сможем. Однако для этого сначала нужно научиться строить графики уравнений.

Построение графиков параметрических кривых

Наиболее простым способом построения графика уравнения в MathCAD’е является параметризация входящих в него переменных друг через друга или через какую-то третью переменную. Что это означает? Поясню на примере. Например, у нас есть уравнение окружности x2 + y2 = 5. Если вы попытаетесь записать функцию f(x, y) = x2 + y2 — 5, а потом построить ее график от x или от y, то вас ожидает разочарование. То, что в итоге выдаст на экран MathCAD, будет так же мало похоже на окружность, как сам MathCAD — на пасьянс «Косынка». Придется придумывать что-то другое. Например, можно подобрать такие функции переменной t, которые, будучи возведенными в квадрат, в сумме тоже дадут пять. Естественно, такими функциями будут тригонометрические — синус и косинус от переменной t, помноженные на корень из пяти. Если мы выразим таким образом x и y через t, то мы параметризуем наше уравнение и уже сможем успешно построить график x(t) от y(t) или же y(t) от x(t) — впрочем, в данном случае в силу симметричности это будет уже не столь важно.

Для того, чтобы решить систему уравнений, нужно просто подобным образом параметризовать и второе уравнение. Вполне возможно, что, как и в нашем примере, оно вполне подойдет для того, чтобы банально выразить x через y или наоборот, после чего построение графика окажется особенно простым (см. соответствующий скриншот). Для нахождения начальных приближений достаточно воспользоваться уже знакомой нам с вами трассировкой — само собой, решением будет точка пересечения двух кривых на уравнении. Для того, чтобы получить более точное значение решения, чем предлагает нам трассировка, нужно, конечно же, подставить полученные с ее помощью координаты точки пересечения графиков в численное решение системы перед Given’ом. Последний скриншот иллюстрирует, что графики мы с вами построили правильно, и с его помощью действительно намного легче искать решение системы двух исходных уравнений. А легче хотя бы уже просто потому, что видно, какого количества корней мы вправе ожидать от нашей системы.

Но работа с трехмерными графиками в MathCAD’е не так проста, как с двумерными, поскольку и сама по себе поверхность — более сложный объект, чем кривая. С поверхностями можно ожидать немалого количества не самого приятного рода сюрпризов, так что лучше о них поговорить более подробно. Этим мы с вами и займемся в следующей статье из цикла о MathCAD’е.

Компьютерная газета. Статья была опубликована в номере 17 за 2008 год в рубрике soft

Mathcad решить аналитически систему уравнений

Уравнение и системы уравнений в математическом пакете Mathcad в символьном виде решаются с использованием специального оператора символьного решения solve в сочетании со знаком символьного равенства, который может быть также введен с рабочей панели “Символика”. Например:

Аналогичные действия при решении уравнений в Mathcad можно выполнить, используя меню “Символика”. Для этого необходимо записать вычисляемое выражение. Затем выделить переменную, относительно которой решается уравнение, войти в меню Символика, Переменная, Разрешить. Например:

В случае, если необходимо упростить полученный результат, используется знак равенства [=]. Например:

При решении некоторых уравнений, результат включает большое количество символов. Mathcad сохраняет его в буфере, а на дисплей выводитcя сообщение: “This array has more elements than can be displayed at one time. Try using the “submatrix” function” – “Этот массив содержит больше элементов, чем может быть отображено одновременно. Попытайтесь использовать функцию “submatrix””. В этом случае рекомендуется использовать численное решение. Или, в случае необходимости, символьное решение может быть выведено и отображено на дисплее.

Символьное решение может быть получено с использованием блока given … find. В этом случае при записи уравнения для связи его левой и правой части использует символ логического равенства “=” с панели инструментов Boolean, например:

Аналогичным способом решаются системы уравнений в символьном виде. Ниже приводятся примеры решения систем уравнений в символьном виде различными способами. При использовании оператора символьного решения solve в сочетании со знаком символьного равенства система уравнений должна быть задана в виде вектора, который вводится вместо левого маркера оператора solve, а перечень переменных, относительно которых решается система, вместо правого маркера. Например:

Пример использования блока given…find для решения системы уравнений: