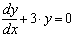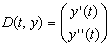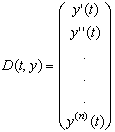Mathcad уравнения в частных производных
При решении дифференциального уравнения искомой величиной является функция. Для ОДУ неизвестная функция — функция одной переменной. Дифференциальные уравнения в частных производных — это дифференциальные уравнения, в которых неизвестной является функция двух или большего числа переменных. Mathcad имеет ряд встроенных функций, предназначенных для решения ОДУ. Каждая из этих функций предназначена для численного решения дифференциального уравнения. В результате решения получается матрица, содержащая значения функции, вычисленные на некотором множестве точек (на некоторой сетке значений). Для каждого алгоритма, который используется при решении дифференциальных уравнений, Mathcad имеет различные встроенные функции. Несмотря на различные методы поиска решения, каждая из этих функций требует, чтобы были заданы по крайней мере следующие величины, необходимые для поиска решения:
- Начальные условия.
- Набор точек, в которых нужно найти решение.
- Само дифференциальное уравнение, записанное в некотором специальном виде, который будет детально описан в этой главе.
В этом разделе описано, как решить ОДУ, используя функцию rkfixed. Раздел начинается с примера того, как решить простейшее дифференциальное уравнение первого порядка. Затем будет показано, как можно решать дифференциальные уравнения более высокого порядка.
Дифференциальные уравнения первого порядка
Дифференциальное уравнение первого порядка — это уравнение, которое не содержит производных выше первого порядка от неизвестной функции. На Рисунке 1 показан пример того, как решить относительно простое дифференциальное уравнение:
с начальными условиями: y(0) = 4
Функция rkfixed на Рисунке 1 использует для поиска решения метод Рунге-Кутты четвертого порядка. В результате решения получается матрица, имеющая два следующих столбца:
- Первый столбец содержит точки, в которых ищется решение дифференциального уравнения.
- Второй столбец содержит значения найденного решения в соответствующих точках.
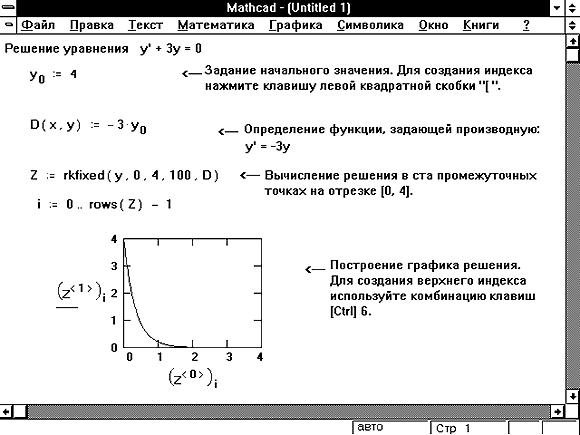
Рисунок 1: Решение дифференциального уравнения первого порядка.
Функция rkfixed имеет следующие аргументы:
| y = | Вектор начальных условий размерности n, где n — порядок дифференциального уравнения или число уравнений в системе (если решается система уравнений). Для дифференциального уравнения первого порядка, как, например, для уравнения, приведенного на Рисунке 1, вектор начальных значений вырождается в одну точку y0 = y(x1). |
| x1, x2 = | Граничные точки интервала, на котором ищется решение дифференциальных уравнений. Начальные условия, заданные в векторе y, — это значение решения в точке x1. |
| npoints = | Число точек (не считая начальной точки), в которых ищется приближенное решение. При помощи этого аргумента определяется число строк (1 + npoints) в матрице, возвращаемой функцией rkfixed. |
| D (x, y) = | Функция, возвращающая значение в виде вектора из n элементов, содержащих первые производные неизвестных функций. |
Наиболее трудная часть решения дифференциального уравнения состоит в определении функции D(x, y), которая содержит вектор первых производных от неизвестных функций. В примере, приведенном на Рисунке 1, было достаточно просто разрешить уравнение относительно первой производной , и определить функцию D(x, y). Иногда, особенно в случае нелинейных дифференциальных уравнений, это может быть трудно. В таких случаях иногда удаётся разрешить уравнение относительно в символьном виде и подставить это решение в определение для функции D(x, y). Используйте для этого команду Решить относительно переменной из меню Символика.
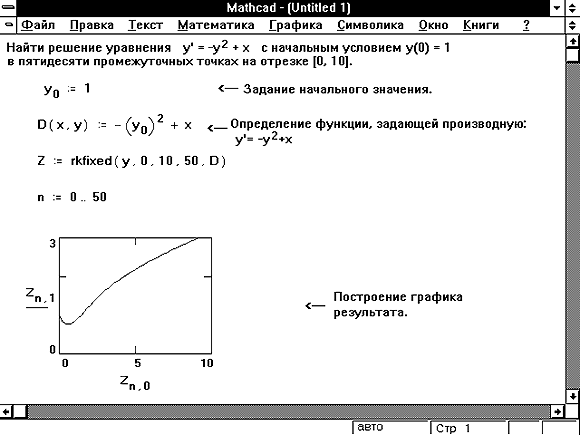
Рисунок 2: Более сложный пример, содержащий нелинейное дифференциальное уравнение.
Дифференциальные уравнения второго порядка
Как только Вы научились решать дифференциальное уравнение первого порядка, можно приступать к решению дифференциальных уравнений более высокого порядка. Мы начнем с дифференциального уравнения второго порядка. Основные отличия от уравнения первого порядка состоят в следующем:
- Вектор начальных условий y теперь состоит из двух элементов: значений функции и её первой производной в начальной точке интервала x1.
- Функция D(t, y) является теперь вектором с двумя элементами:
Пример, приведенный на Рисунке 3, показывает, как решить следующее дифференциальное уравнение второго порядка:
Рисунок 3: Решение дифференциального уравнения второго порядка.
Уравнения более высокого порядка
Методика решения дифференциальных уравнений более высокого порядка является развитием методики, которая применялась для решения дифференциальных уравнений второго порядка. Основное различие состоит в следующем:
- Вектор начальных значений y теперь состоит из n элементов, определяющих начальные условия для искомой функции и ее производных y, y’ , y». y (n-1)
- Функция D является теперь вектором, содержащим n элементов:
Пример, приведенный на Рисунке 4, показывает, как решить следующее дифференциальное уравнение четвертого порядка:
с начальными условиями:
Рисунок 4: Решение дифференциального уравнения более высокого порядка.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Mathcad уравнения в частных производных
11.3.1. Параболические и гиперболические уравнения
Разработчики впервые применили дополнительные встроенные функции для решения параболических и гиперболических уравнений в частных производных в версии Mathcad 11, отлично осознавая значимость этих задач для современного исследователя и инженера. Предусмотрены два варианта решения: при помощи вычислительного блока Given/pdeso l ve , а также при помощи встроенной функции numo l . Первый путь проще в применении и нагляднее, зато второй позволяет автоматизировать процесс решения уравнений в частных производных, например, если нужно включить его в качестве составного шага в более сложную Mathcad-программу.
Вычислительный блок Given /pdesolve
Встроенная функция pdesolve применяется в рамках вычислительного блока, начинающегося ключевым словом Given , и пригодна для решения различных гиперболических и параболических уравнений. Она предназначена для решения одномерного уравнения (или системы уравнений) в частных производных (того, которое определит пользователь в рамках вычислительного блока Given ), зависящего от времени t и пространственной координаты х , имеет целый набор различных аргументов и работает следующим образом:
- pdesolve(u,x,xrange,t,trange,[xpts],[tpts])) — Возвращает скалярную (для единственного исходного уравнения) или векторную (для системы уравнений) функцию двух аргументов (x,t) , являющуюся решением дифференциального уравнения (или системы уравнений) в частных производных. Результирующая функция получается интерполяцией сеточной функции, вычисляемой согласно разностной схеме:
- u — явно заданный вектор имен функций (без указания имен аргументов), подлежащих вычислению. Эти функции, а также граничные условия (в форме Дирихле или Неймана) должны быть определены пользователем перед применением функции pdeso l ve в вычислительном блоке после ключевого слова Given . Если решается не система уравнений в частных производных, а единственное уравнение, то, соответственно, вектор и должен содержать только одно имя функции и вырождается в скаляр;
- х — пространственная координата (имя аргумента неизвестной функции);
- xrange — пространственный интервал, т. е. вектор значений аргумента х для граничных условий. Этот вектор должен состоять из двух действительных чисел (представляющих левую и правую границу расчетного интервала);
- t — время (имя аргумента неизвестной функции);
- t range — расчетная временная область: вектор значений аргумента t, который должен состоять из двух действительных чисел (представляющих левую и правую границу расчетного интервала по времени);
- xpts — количество пространственных точек дискретизации (может не указываться явно, в таком случае будет подобрано программой автоматически);
- tpts — количество временных слоев, т. е. интервалов дискретизации по времени (также может не указываться пользователем явно).
В качестве примера использования функции pdeso l ve (листинг 11.4) используем то же самое одномерное уравнение теплопроводности (11.5) с граничными и начальными условиями (11.6) и (11.7).
Листинг 11.4. Решение одномерного уравнения теплопроводности
Для корректного использования функции pdeso l ve предварительно, после ключевого слова Given , следует записать само уравнение и граничные условия при помощи логических операторов (для их ввода в Mathcad существует специальная панель). Обратите внимание, что уравнение должно содержать имя неизвестной функции u(x,t) вместе с именами аргументов (а не так, как она записывается в пределах встроенной функции pdeso l ve ). Для идентификации частных производных в пределах вычислительного блока следует использовать нижние индексы, например, uxx(,t) , для обозначения второй производной функции и по пространственной координате х .
Как видно из рис. 11.14, на котором изображены результаты расчетов по листингу 11.4, встроенная функция с успехом справляется с уравнением диффузии, отыскивая уже хорошо знакомое нам решение. Заметим, что использование встроенной функции pdeso l ve связано с довольно громоздкими вычислениями, которые могут отнимать существенное время.
Как вы можете заметить, выбирать величину шага по пространственной и временной переменным может как сам алгоритм, так и пользователь (неявным образом, через число узлов сетки). Читателю предлагается повторить вычисления листинга 11.4 для различных комбинаций параметров (главным образом, числа узлов сетки), чтобы проверить, в каких случаях алгоритм встроенной функции справляется с задачей, выдавая верное решение, а в каких дает сбой.
Рис. 11.14. Решение уравнения диффузии тепла при помощи встроенной функции pdesoдve (листинг 11.4)
Пример: волновое уравнение
Приведем еще один пример применения функции pdesoive для решения уравнений в частных производных. Рассмотрим одномерное волновое уравнение, которое описывает, например, свободные колебания струны музыкального инструмента:
Здесь неизвестная функция u(x,t) описывает динамику смещения профиля струны относительно невозмущенного (прямолинейного) положения, а параметр с характеризует материал, из которого изготовлена струна.
Как вы видите, уравнение (11.11) содержит производные второго порядка, как по пространственной координате, так и по времени. Для того чтобы можно было использовать встроенную функцию pdesolve , необходимо переписать волновое уравнение в виде системы двух уравнений в частных производных, введя вторую неизвестную функцию v=ut . Программа для решения волнового уравнения приведена в листинге 11.5, а результат— на рис. 11.15.
Листинг 11.5. Решение волнового уравнения
Рис. 11.15. Решение волнового уравнения (продолжение листинга 11.5)
Встроенная функция numol
Альтернативный вариант решения дифференциальных уравнений в частных производных заключается в применении еще одной встроенной функции numo |, которая реализует тот же самый алгоритм сеток, позволяя вручную задать большинство его параметров:
- numol(xrange,xpts,trange,tpts,Npde,Nae,rhs,init,bc) — Возвращает матрицу решения дифференциального уравнения в частных производных, представляющую искомую сеточную функцию в каждой точке по пространственной (по строкам) и временной координате (по столбцам). Если решается не одно уравнение, а система уравнений, то результатом является составная матрица, образованная путем слияния (слева-направо) матриц со значениями каждой искомой сеточной функции:
- Npde — общее количество дифференциальных уравнений в частных производных в системе;
- Nae — общее количество дополнительных алгебраических уравнений, которые также могут входить в систему;
- rhs — векторная функция, определяющая систему дифференциальных и алгебраических уравнений (формат этого и двух следующих матричных параметров объяснен в листинге 11.9);
- init — векторная функция, определяющая начальные условия для каждой неизвестной функции;
- be — функциональная матрица граничных условий;
- xrange — пространственный интервал, т. е. вектор значений аргумента х для граничных условий. Этот вектор должен состоять из двух действительных чисел (представляющих левую и правую границу расчетного интервала);
- xpts — количество пространственных точек дискретизации (может не указываться явно, в таком случае будет подобрано программой автоматически);
- trange — расчетная временная область: вектор значений аргумента t, который должен состоять из двух действительных чисел (представляющих левую и правую границу расчетного интервала по времени);
- tpts — количество временных слоев, т. е. интервалов дискретизации по времени (также может не указываться пользователем явно);
Пример решения волнового уравнения при помощи функции numol приведен в листинге 11.6, особое внимание в котором мы призываем уделить формату представления векторов rhs , init и be , а также принципу извлечения отдельных сеточных решений из матрицы-результата. График решения, показанный на рис. 11.16, полезно сравнить с результатом применения вычислительного блока из предыдущего раздела (см. листинг 11.5 и рис. 11.15).
Листинг 11.6 . Решение волнового уравнения при помощи функции numol
Как вы видите, функция numol имеет еще большее число аргументов, нежели pdesolve , и позволяет автоматизировать применение метода сеток. Однако пользоваться ею намного сложнее, чем вычислительным блоком, поскольку и уравнения, и начальные и граничные условия должны быть записаны в специальном формате. Применение функции numol оправданно, когда необходимо включить решение уравнений в частных производных в более сложные вычисления в качестве подпрограммы, организовать серию расчетов с меняющимся параметром, подготовить анимацию графиков решения и т. п.
Рис. 11.16. Решение волнового уравнения (продолжение листинга 11.6)
Именно в целях визуализации решения параболических и гиперболических уравнений в частных производных использование функции numol наиболее полезно. График решения динамических уравнений (зависящих от времени t) выглядит намного эффектнее и воспринимается несравненно лучше, если он оформлен в виде анимации. Для создания анимационных роликов расчетное время следует выразить через константу FRAME и затем применить команду View / Animate (Вид / Анимация) (см. разд. 13.3.2).
MathCAD — это просто! Часть 23. Внутренняя кухня решения дифференциальных уравнений. Дифференциальные уравнения в частных производных
Хотя мы с вами говорим о решении дифференциальных уравнений в среде MathCAD уже, в общем-то, довольно-таки давно, тем не менее, тема эта по- прежнему остается не до конца раскрытой. Почему? Потому, что дифференциальным уравнениям и их решению в мире посвящено гигантское количество различных научных работ и книг — пожалуй, столько их не посвящалось больше ни одному вопросу прикладного применения математики.
Дифференциальные уравнения сегодня — это, прежде всего, основа для всех физических и химических расчетов, применяемых в промышленности и науке. И потому без дифференциальных уравнений не может обойтись в рамках своей профессиональной деятельности ни один специалист технического или естественнонаучного профиля. И чем лучше мы с вами научимся решать дифференциальные уравнения с помощью MathCAD, тем легче вам будет разбираться с ними в тот момент, когда они понадобятся вам для выполнения какой-либо порученной вам работы. Разговор о дифференциальных уравнениях в MathCAD просто не может быть полным без двух вещей. Первая из них — это краткий, слишком краткий для того, чтобы быть действительно полезным, рассказ о внутренних механизмах решения дифференциальных уравнений в этой мощной математической среде, то есть об используемых MathCAD’ом алгоритмах их численного интегрирования. Увы, объем газетной статьи ограничен, и рассказывать подробно настолько, насколько хотелось бы, у меня нет возможности. Вторая же такая вещь — рассказ о решении дифференциальных уравнений в частных производных, к которым относятся практически все уравнения математической и теоретической физики. Конечно, вещи это довольно сложные, но я постараюсь сделать их понятными для каждого из читателей серии «MathCAD — это просто». Ну, а судить, насколько хорошо у меня это выйдет, уже дело ваше.
Численное интегрирование обыкновенных дифференциальных уравнений методом Рунге-Кутта четвертого порядка
Для того, чтобы понять, как именно работают алгоритмы численного решения дифференциальных уравнений, нужно вспомнить, что именно мы делаем, решая дифференциальное уравнение в MathCAD’е. Вспомнили? Правильно, мы интегрируем. Значит, мы находим первообразную некоторой функции, которую в простейшем случае можем записать как f(x,y), где y и будет решением нашего дифференциального уравнения. Для того, чтобы объяснять дальше, нужно напомнить, что же такое производная — ведь именно ею является наша функция f(x, y) по отношению к своей искомой первообразной. Производная — это предел приращения функции к пределу приращения своего аргумента (или своих аргументов, если таковых имеется больше, чем один). Однако пределы — это всего лишь математическая абстракция, какой бы хорошей и удобной она ни была. То есть мы не можем в реальном мире оперировать бесконечно малым приращением ни функции, ни ее аргументов, если хотим с их помощью вычислить саму производную. Выход из этой ситуации напрашивается самый простой и логичный — перейти от бесконечно малого приращению к малому, но все же конечному. Говорят, что дифференциальное уравнение при этом заменяется на разностное, и для его решения применяются специальные разностные методы.
Самым распространенным методом решения дифференциальных уравнений в численном виде является метод Рунге-Кутта четвертого порядка, который из-за его повсеместной распространенности обычно называют просто методом Рунге-Кутта. Этот метод разработан еще в начале XX века немецкими математиками Карлом Рунге и Мартином Вильгельмом Куттом и с тех пор, как появились первые вычислительные машины, используется для численного решения дифференциальных уравнений самым что ни на есть активным образом. В MathCAD’е метод Рунге-Кутта в его классическом виде реализован в функции rkfixed. Ограничения, накладываемые ею на решаемые с ее помощью уравнения, — это те самые ограничения, которые на них накладывает метод Рунге-Кутта. Алгоритм Рунге-Кутта итерационный, то есть для вычисления значения функции с заданной точностью нужно выполнить вычисления несколько раз, и для каждого следующего вычисления используются результаты предыдущего. Записать это в виде формул можно следующим образом:
Самая нижняя из всех формул — это исходное уравнение, которое мы решаем указанным методом, а коэффициенты k называются прогоночными коэффициентами. Как видите, для того, чтобы вычислить по этим формулам хоть одно значение y, нужно воспользоваться начальным (нулевым) значением y. То есть этот метод очень хорошо подходит для решения задачи Коши, а вот если встретится краевая задача, то здесь уже надо искать другой метод. Как можно понять из формул, h — это величина шага интегрирования. Об этой величине я рассказывал тогда, когда приоткрывал завесу тайны над «кухней» численного интегрирования в MathCAD’е, а потому останавливаться на ней повторно и рисовать графики, иллюстрирующие ее геометрическую интерпретацию, я не буду. Почему рассмотренный нами алгоритм называется алгоритмом четвертого порядка? Дело в том, что суммарная погрешность при вычислении функции по записанным выше формулам составляет величину порядка h4. При достаточно малых h это очень хорошая точность, и именно поэтому метод Рунге-Кутта получил такое широкое распространение. Конечно, рассмотренный нами метод численного решения дифференциальных уравнений не настолько универсален, насколько нам того хотелось бы, но разработчики MathCAD существенно упростили нам задачу, реализовав удобную и мощную функцию Odesolve, комбинирующую в себе возможности нескольких разных алгоритмов численного решения обыкновенных дифференциальных уравнений. Если вдруг вы решите проникнуть глубже в тайны методов численного решения дифференциальных уравнений, то делать это лучше всего с помощью соответствующих учебников, которых в библиотеках и в интернете можно найти великое множество.
Решение дифференциальных уравнений в частных производных
Что ж, давайте уже перейдем к завершающему наш разговор о дифференциальных уравнениях в MathCAD’е вопросу — решению дифференциальных уравнений в частных производных. Дифференциальным уравнением в частных производных называется уравнение относительно функции нескольких переменных (обязательно более чем одной), содержащее саму эту функцию (что, впрочем, необязательно) и ее частные производные по различным аргументам (вот это уже необходимо). Классическими уравнениями в частных производных являются уравнения математической физики — например, такие, как уравнение колебаний мембраны или даже струны; уравнение теплопроводности, описывающее перенос тепловой энергии в веществах; уравнение Шредингера, на котором построена вся квантовая механика. Решать уравнения в частных производных обычно еще сложнее, чем обыкновенные дифференциальные уравнения, однако, как вы сами сможете убедиться, это утверждение можно не считать справедливым в тех случаях, когда вам на помощь приходит такая мощная математическая среда, как MathCAD. Давайте попробуем решить с помощью MathCAD’а уже упоминавшееся буквально пару строчек назад уравнение теплопроводности, которое можно записать в следующем виде:
Решать его будем с помощью уже частично знакомого вам блока Given…Pdesolve. Он весьма схож с блоком Given. Odesolve, который мы использовали для обыкновенных дифференциальных уравнений, но имеются некоторые отличия. Так, например, производные для этого блока нужно задавать в индексной форме записи. То есть первая производная от y по x будет записана как yx. В MathCAD’е для записи производных в нижнем регистре нажмите кнопку «.» («ю» на русской клавиатуре). Вот таким образом будет выглядеть наше решение дифференциального уравнения в частных производных:
То, что стоит сразу непосредственно после Given, думаю, в каких-либо подробных прояснениях не нуждается, потому что это, собственно говоря, и есть то самое дифференциальное уравнение, которое мы с вами усиленно решаем. Сразу же следом за ним идут начальные условия по времени и граничные условия по координате — такие условия называются условиями Дирихле. Но самое важное, в общем-то, не они, а та функция, с помощью которых наш набор условий превращается в решенное дифференциальное уравнение — это функция Pdesolve. Первый ее параметр — это название функции или вектор функций, которые заданы в блоке Given. Второй и третий параметры — это один из аргументов функции и вектор из его начального и конечного значений. Здесь нужно внимательно следить за тем, чтобы эти значения в блоке Given обязательно совпадали с параметрами самой Pdesolve — в случае их взаимного несоответствия система MathCAD выдаст ошибку. Следующие два (или четыре, или шесть — все зависит от исходной функции и решаемого уравнения) параметра также обозначают аргумент и его граничные значения. Ну, а завершают список параметров функции Pdesolve количество шагов по каждой из переменных. Совсем не обязательно делать их равными для всех переменных — надо смотреть на особенности самого уравнения, а также начальных и граничных условий. Чтобы визуализировать результаты решения, можно воспользоваться нашими знаниями о построении графиков в MathCAD’е и построить трехмерный график (см. соответствующий рисунок). Вопрос на засыпку: какая из осей изображает время? Вот и проверим, насколько вы разобрались в свое время с графиками.
Конечно, для таких уравнений, где одна из переменных является временем, лучше строить не трехмерные графики, а двумерные, но анимированные. Как они делаются, я вам уже имел удовольствие рассказывать, а потому вы, безо всяких сомнений, успешно справитесь с их созданием.
Что ж, как видите, и в глубинах MathCAD’а, в которых идет решение дифференциальных уравнений численными методами, все оказалось вовсе не так уж и сложно. Конечно, мы с вами разобрали только самый простой случай, но ведь перед нами, согласитесь, и не стоит задачи написать собственную математическую среду наподобие MathCAD, а потому мы можем позволить себе не разбираться в тонкостях реализации разных методов, а просто предоставить MathCAD’у самому разбираться с подсунутыми нами уравнениями. С дифференциальными уравнениями в частных производных тоже все оказалось не так уж сложно, потому что разработчики MathCAD постарались максимально унифицировать процесс их решения с процессом решения обыкновенных дифференциальных уравнений. Так что не нужно бояться дифференциальных уравнений, если под рукой есть MathCAD. Рано или поздно, так или иначе, но они падут под натиском этого грозного математического «оружия».
Компьютерная газета. Статья была опубликована в номере 37 за 2008 год в рубрике soft
http://sistemair.ru/dok/mathcad12/Glava_11/Index10.htm
http://nestor.minsk.by/kg/2008/37/kg83705.html