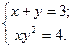Matlab как найти корень уравнения

Решение нелинейных уравнений в Matlab

Доброго времени суток. В этой статье мы разберем решение простых нелинейных уравнений с помощью средств Matlab. Посмотрим в действии как стандартные функции, так и сами запрограммируем три распространенных метода для решения нелинейных уравнений.

Общая информация

Уравнения, которые содержат переменные, находящиеся в степенях, отличающихся от единицы, или имеющие нелинейные математические выражения (корень, экспонента, логарифм, синус, косинус и т.д.), а также имеющие вид f(x) = 0 называются нелинейными. В зависимости от сложности такого уравнения применяют методы для решения нелинейных уравнений.

В этой статье, помимо стандартных функций Matlab, мы рассмотрим следующие методы:

• Метод перебора
• Метод простых итераций
• Метод половинного деления

Рассмотрим коротко их алгоритмы и применим для решения конкретной задачи.

Стандартные функции Matlab

Для решения нелинейных уравнений в Matlab есть функция fzero. Она принимает в качестве аргументов саму функцию, которую решаем, и отрезок, на котором происходит поиск корней нелинейного уравнения.

И сразу же разберем пример:

Решить нелинейное уравнение x = exp(-x), предварительно определив интервалы, на которых существуют решения уравнения.

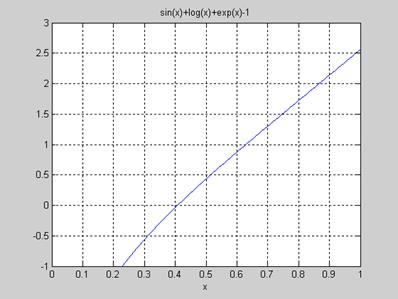
Итак, для начала следует привести уравнение к нужному виду: x — exp(-x) = 0 , а затем определить интервалы, в которых будем искать решение уравнения. Методов для определения интервалов множество, но так как пример достаточно прост мы воспользуемся графическим методом.

Здесь задали примерные границы по оси x, чтобы можно было построить график и посмотреть как ведет себя функция. Вот график:

Из графика видно, что на отрезке [0;1] есть корень уравнения (там, где y = 0), соответственно в дальнейшем будем использовать этот интервал. Чем точнее выбран интервал, тем быстрее метод придет к решению уравнения, а для сложных уравнений правильный выбор интервала определяет погрешность, с которой будет получен ответ.

С помощью стандартной функции Matlab находим корень нелинейного уравнения и выводим. Теперь для проверки отобразим все это графически:

Как вы видите, все достаточно точно просчиталось. Теперь мы исследуем эту же функцию с помощью других методов и сравним полученные результаты.

Метод перебора Matlab

Самый простой метод, который заключается в том, что сначала задается какое то приближение x (желательно слева от предполагаемого корня) и значение шага h. Затем, пока выполняется условие f(x) * f(x + h) > 0, значение x увеличивается на значение шага x = x + h. Как только условие перестало выполняться — это значит, что решение нелинейного уравнения находится на интервале [x; x + h].

Теперь реализуем метод перебора в Matlab:

Лучше всего создать новый m-файл, в котором и прописать код. После вызова получаем такой вывод:

Функцию объявляем с помощью очень полезной команды inline, в цикле пока выполняется условие отсутствия корней (или их четного количества), прибавляем к x значение шага. Очевидно, что чем точнее начальное приближение, тем меньше итераций необходимо затратить.

Метод простых итераций Matlab

Этот метод заключается в том, что функцию преобразуют к виду: x = g(x). Эти преобразования можно сделать разными способами, в зависимости от вида начальной функции. Помимо этого следует задать интервал, в котором и будет производиться итерационный процесс, а также начальное приближение. Сам процесс строится по схеме x_n= g(x_n-1). То есть итерационно проходим от предыдущего значения к последующему.

Процесс заканчивается как только выполнится условие: , то есть, как только будет достигнута заданная точность. И сразу же разберем реализацию метода простых итераций в Matlab для примера, который был приведен выше.

Здесь должно быть все понятно, кроме одного: зачем задавать число итераций? Это нужно для того, чтобы программа не зацикливалась и не выполняла ненужные итерации, а также потому что не всегда программа может просчитать решение с нужной точностью — поэтому следует ограничивать число итераций.

А вот и вывод программы:

Очевидно, что метод простых итераций работает гораздо быстрее и получает точное решение.

Метод половинного деления Matlab

Метод достаточно прост: существует отрезок поиска решения [a;b], сначала находят значение функции в точке середины c, где c = (a+b)/2. Затем сравнивают знаки f(a) и f(c). Если знаки разные — то решение находится на отрезке [a;c], если нет — то решение находится на отрезке [c;b]. Таким образом мы сократили область в 2 раза. Такое сокращение происходит и дальше, пока не достигнем заданной точности.

Перейдем к реализации метода в Matlab:

Все самое важное происходит в цикле: последовательно сокращаем область нахождения решения, пока не будет достигнута заданная точность.
Вот что получилось в выводе:

Этот метод хорошо работает, когда правильно определен интервал, на котором находится решение. Тем не менее, метод простых итераций считается наиболее точным и быстрым.

Заключение

Сегодня мы рассмотрели решение нелинейных уравнений в Matlab. Теперь нам известны методы перебора, половинного деления, простых итераций. А также, когда нам не важно реализация метода, то можно использовать стандартную функцию в Matlab.

На этом все — спасибо за внимание. В следующей статье мы разберем решение систем нелинейных уравнений в matlab.

MATLAB — алгебра

До сих пор мы видели, что все примеры работают как в MATLAB, так и в его GNU, альтернативно называемом Octave. Но для решения основных алгебраических уравнений и MATLAB, и Octave немного отличаются, поэтому мы постараемся охватить MATLAB и Octave в отдельных разделах.

Мы также обсудим факторизацию и упрощение алгебраических выражений.

Решение основных алгебраических уравнений в MATLAB

Функция решения используется для решения алгебраических уравнений. В простейшем виде функция решения принимает в качестве аргумента уравнение, заключенное в кавычки.

Например, давайте решим для х в уравнении х-5 = 0

MATLAB выполнит приведенный выше оператор и вернет следующий результат —

Вы также можете вызвать функцию решения как —

MATLAB выполнит приведенный выше оператор и вернет следующий результат —

Вы можете даже не включать правую часть уравнения —

MATLAB выполнит приведенный выше оператор и вернет следующий результат —

Если в уравнение входит несколько символов, то по умолчанию MATLAB предполагает, что вы решаете для x, однако функция решения имеет другую форму —

где вы также можете упомянуть переменную.

Например, давайте решим уравнение v — u — 3t 2 = 0, для v. В этом случае мы должны написать —

MATLAB выполнит приведенный выше оператор и вернет следующий результат —

Решение основных алгебраических уравнений в октаве

Функция корней используется для решения алгебраических уравнений в Octave, и вы можете написать приведенные выше примеры следующим образом:

Например, давайте решим для х в уравнении х-5 = 0

Octave выполнит приведенный выше оператор и вернет следующий результат —

Вы также можете вызвать функцию решения как —

Octave выполнит приведенный выше оператор и вернет следующий результат —

Решение квадратичных уравнений в MATLAB

Функция решения также может решать уравнения более высокого порядка. Он часто используется для решения квадратных уравнений. Функция возвращает корни уравнения в массиве.

В следующем примере решается квадратное уравнение x 2 -7x +12 = 0. Создайте файл сценария и введите следующий код —

Когда вы запускаете файл, он показывает следующий результат —

Решение квадратичных уравнений в октаве

В следующем примере решается квадратное уравнение x 2 -7x +12 = 0 в октаве. Создайте файл сценария и введите следующий код —

Когда вы запускаете файл, он показывает следующий результат —

Решение уравнений высшего порядка в MATLAB

Функция решения также может решать уравнения более высокого порядка. Например, давайте решим кубическое уравнение как (x-3) 2 (x-7) = 0

MATLAB выполнит приведенный выше оператор и вернет следующий результат —

В случае уравнений более высокого порядка корни длинные, содержащие много членов. Вы можете получить числовое значение таких корней, преобразовав их в двойные. В следующем примере решается уравнение четвертого порядка x 4 — 7x 3 + 3x 2 — 5x + 9 = 0.

Создайте файл сценария и введите следующий код —

Когда вы запускаете файл, он возвращает следующий результат —

Обратите внимание, что последние два корня являются комплексными числами.

Решение уравнений высшего порядка в октаве

В следующем примере решается уравнение четвертого порядка x 4 — 7x 3 + 3x 2 — 5x + 9 = 0.

Создайте файл сценария и введите следующий код —

Когда вы запускаете файл, он возвращает следующий результат —

Решение системы уравнений в MATLAB

Функция решения также может быть использована для генерации решений систем уравнений, включающих более одной переменной. Давайте рассмотрим простой пример, чтобы продемонстрировать это использование.

Давайте решим уравнения —

Создайте файл сценария и введите следующий код —

Когда вы запускаете файл, он показывает следующий результат —

Таким же образом вы можете решать большие линейные системы. Рассмотрим следующую систему уравнений —

Решающая система уравнений в октаве

У нас есть немного другой подход к решению системы ‘n’ линейных уравнений с ‘n’ неизвестными. Давайте рассмотрим простой пример, чтобы продемонстрировать это использование.

Давайте решим уравнения —

Такая система линейных уравнений может быть записана в виде единого матричного уравнения Ax = b, где A — матрица коэффициентов, b — вектор столбцов, содержащий правую часть линейных уравнений, а x — вектор столбцов, представляющий решение как показано в программе ниже —

Создайте файл сценария и введите следующий код —

Когда вы запускаете файл, он показывает следующий результат —

Таким же образом, вы можете решить большие линейные системы, как указано ниже —

Разложение и сбор уравнений в MATLAB

Функция расширения и сбора расширяет и собирает уравнение соответственно. Следующий пример демонстрирует понятия —

Когда вы работаете со многими символическими функциями, вы должны объявить, что ваши переменные являются символическими.

Создайте файл сценария и введите следующий код —

Когда вы запускаете файл, он показывает следующий результат —

Расширяя и собирая уравнения в октаве

Вам нужно иметь символьный пакет, который обеспечивает расширение и функцию сбора для расширения и сбора уравнения, соответственно. Следующий пример демонстрирует понятия —

Когда вы работаете со многими символическими функциями, вы должны объявить, что ваши переменные являются символическими, но у Octave другой подход к определению символических переменных. Обратите внимание на использование Sin и Cos , которые также определены в символической упаковке.

Создайте файл сценария и введите следующий код —

Когда вы запускаете файл, он показывает следующий результат —

Факторизация и упрощение алгебраических выражений

Факторная функция разлагает выражение, а функция упрощения упрощает выражение. Следующий пример демонстрирует концепцию —

пример

Создайте файл сценария и введите следующий код —

Когда вы запускаете файл, он показывает следующий результат —

Решение уравнений и их систем – команда solve

Дата добавления: 2015-06-12 ; просмотров: 5229 ; Нарушение авторских прав

Для решения систем уравнений и одиночных уравнений служит команда

solve(expr1, expr2. exprN, var1, var2. varN). Она возвращает значения переменных varI, при которых соблюдаются равенства, заданные выражениями exprI. Если в выражениях не используются знаки равенства, то полагается, что exprI = 0.

Результат может быть возвращен в следующих формах:

для одного уравнения и одной переменной решение возвращается в виде одномерного или многомерного массива ячеек;

при одинаковом числе уравнений и переменных решение возвращается в упорядоченном по именам переменных виде.

Команда solve позволяет найти не только вещественные, но и комплексные решения систем уравнений и одиночных уравнений. Справку по этой команде можно получить, введя команду doc solve.

Решить уравнение x 3 — 1 = 0.

В результате получены три разных значения корня x₁ = 1, x₂ = , x₃ = , которые хранятся соответственно в элементах S(1), S(2), S(3) массива S.

С помощью subs (разд. 7.7) подставим найденные значения корней в выражение x 3 — 1:

Выражение x 3 — 1 принимает значение 0 при подстановке любого из найденных корней, поэтому x₁, x₂, x₃ являются точными корнями уравнения x 3 — 1 = 0.

Команда roots (см. разд. 6.1) нашла бы только приближенные значения корней уравнения x 3 — 1 = 0. В общем случае полиномиальное уравнение степени выше 4 не может иметь точного решения, выраженного с помощью радикалов.

Команда solve позволяет решать уравнения, представленные в аналитическом виде.

Решить квадратное уравнение ax 2 +bx+c = 0.

Команда solve возвратила известные выражения корней x_1,2 = квадратного уравнения ax 2 +bx+c = 0. Точно также можно выразить с помощью радикалов решения кубического уравнения ax 3 +bx 2 +cx+d = 0, хотя эти выражения достаточно сложные.

Решить трансцендентное уравнение x lnx +1 — 1 = 0.

В данном случае solve нашла точные значения корней x₁ = 1, x₂ = e −1 .

Решить трансцендентное уравнение lnx + 3 — x = 0.

Команда solve возвратила значения корней, выраженные через функцию Ламберта.

Команда vpa возвращает приближенные значения этих корней, вычисленные с 20 значащими цифрами:

Каждый из приближенных корней этого уравнения был найден по отдельности в разделе 6.2 с помощью команды fzero. Отметим, что команда solve нашла приближенные значения двух корней одновременно с высокой точностью. При этом не пришлось графически определять интервалы изоляции корней.

Решение любого трансцендентного уравнения, в том числе и тригонометрического (разд. 7.17), достаточно сложная и серьезная проблема. Иногда solve возвращает неверные решения.

Решить трансцендентное уравнение sinx lnsinx +x x — 2 = 0.

Найденное решение неверное, т. к. оно не прошло проверку подстановкой.

Команда solve может возвратить не все решения.

Решить трансцендентное уравнение sinx+lnx+e x — 1 = 0.

Возвратив приближенный комплексный корень уравнения x₁ = -3,0553 — 1,7145i, solve не нашла вещественный корень. С помощью команды ezplot (разд. 7.16) графически определяем, что он находится вблизи значения 0,4 (рис. 7.2):

Вещественный корень со стартовым приближением 0,4 найдем с помощью команды fzero(разд. 6.2):

Итак, приближенное значение вещественного корня x₂=0,4072.

Перейдем теперь к системам уравнений.

Решить систему уравнений

Результатом выполнения команды solve является структура S с полями x и y, каждое из которых содержит символьное представление решения:

Выведем в командное окно содержимое структуры:

Для проверки подставим в выражения Y1 = x+y — 3 и Y2 = xy 2 — 4 вначале первое решение, а затем второе:

>> disp(subs([Y1 Y2],[x y],[S.x(1) S.y(1)])

>> disp(subs([Y1 Y2],[x y],[S.x(2) S.y(2)])

Как видим, найдены точные решения, т. к. выражения Y1 и Y2 при их подстановке обратились в 0.

Команда solve допускает использование символьных переменных в качестве выходных аргументов. Эквивалентное обращение к solve в предыдущем примере имеет вид:

Команда solve позволяет решать системы уравнений, заданные в аналитическом виде.

Решить систему уравнений относительно x, y, z