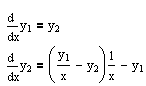Matlab решение дифференциальных уравнений 2 порядка

Решение ОДУ в Matlab

Доброго времени суток! Сегодня мы поговорим о решении ОДУ (обыкновенных дифференциальных уравнений) в Matlab. Перед тем как мы начнём обсуждать данную тему, советую вам ознакомиться с темой: Численное дифференцирование в Matlab, чтобы лучше понимать теоретическую составляющую решения ОДУ.

Обыкновенные дифференциальные уравнения

С помощью дифференциальных уравнений можно описать разные задачи: движения системы, взаимодействующих материальных точек, химической кинетики и т.д. Различают три типа задач для систем диф. уравнений:

• Задача Коши
• Краевая задача
• Задача на собственные значения

Кратко расскажу о их сути:

Задача Коши предполагает дополнительные условия в виде значения функции в определённой точке.
Краевая задача подразумевает поиск решения на заданном отрезке с краевыми (граничными) условиями в концах интервала или на границе области.
Задача на собственные значения — помимо искомых функций и их производных, в уравнение входят дополнительное несколько неизвестных параметров, которые являются собственными значениями.

Методы решения дифференциальных уравнений

Решение ОДУ в Matlab и не только, в первую очередь, сводится к выбору порядка численного метода решения. Порядок численного метода не связан с порядком дифференциального уравнения. Высокий порядок у численного метода означает его скорость сходимости.

В случае большого интервала, с помощью алгоритмов с низким порядком сжимают интервал с решениями и находят приблизительные корни, а затем уже уточняют корни с помощью методов с высоким порядком.

Решение обыкновенных дифференциальных уравнений в Matlab можно реализовать «своими ручками», прописав алгоритм по разным схемам. Но также в Matlab есть встроенные функции, выполняющие все стандартные задачи.

Метод Рунге-Кутта первого порядка

Методы Рунге-Кутта представляют собой разложения в ряд Тейлора и от количества использованных элементов ряда зависит порядок этого метода. Следовательно, помимо Рунге-Кутта первого порядка, вы сможете увидеть методы других порядков. Иногда их называют другими именами.

Например, Метод Рунге-Кутта первого порядка, также известен как Метод Эйлера или Метод ломаных. Информацию о его математическом и графическом представлении советую поискать в гугл. Мы же поговорим о том, как Метод Рунге-Кутта первого порядка реализуется в Matlab для решения ОДУ. Например:

Решить и привести график ошибки уравнения y’ = y*x методом Рунге-Кутта первого порядка (Методом Эйлера, Методом ломаных).

Погрешность Метода Рунге-Кутта 1 порядка

» data-medium-file=»https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/Рунге-1-погрешность.png?fit=300%2C236&ssl=1″ data-large-file=»https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/Рунге-1-погрешность.png?fit=622%2C489&ssl=1″ loading=»lazy» src=»https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/%D0%A0%D1%83%D0%BD%D0%B3%D0%B5-1-%D0%BF%D0%BE%D0%B3%D1%80%D0%B5%D1%88%D0%BD%D0%BE%D1%81%D1%82%D1%8C.png?resize=622%2C489″ alt=»Погрешность метода 1 порядка» width=»622″ height=»489″ srcset=»https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/Рунге-1-погрешность.png?w=629&ssl=1 629w, https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/Рунге-1-погрешность.png?resize=300%2C236&ssl=1 300w» sizes=»(max-width: 622px) 100vw, 622px» data-recalc-dims=»1″ />
На данном графике показана зависимость величины ошибки от шага.

Метод Рунге-Кутта второго порядка

Также известен как Метод Эйлера-Коши. Как видите, во второй части уравнения происходит обращения к следующему шагу. Но как тогда быть, если нам ещё не известен следующий шаг? Всё просто. Метод Рунге-Кутта второго порядка — это всё тот же метод первого порядка, однако, на половине шага происходит нахождение «первичного» решения, а затем происходит его уточнение. Это позволяет поднять порядок скорости сходимости до двух.

Решить и привести график ошибки уравнения u’ = u*x методом Рунге-Кутта второго порядка.

По сравнению с Рунге-Куттом первого порядка изначальная ошибка уже гораздо меньше.

Мы не будем говорить о третьем порядке, потому что задачи на третий порядок встречаются редко, но если будет необходимо, пишите в комментариях, выложу.

Метод Рунге-Кутта четвёртого порядка

Метод Рунге-Кутта четвёртого порядка считается самым распространённым. Тем не менее, работает он аналогично второму и третьему порядку.

Решить и привести график ошибки уравнения u’ = u*x методом Рунге-Кутта четвёртого порядка.

Как видите, на последней картинке размерность ошибки на столько мала, что пришлось воспользоваться loglog() для лучшей видимости.

Решение ОДУ в Matlab стандартными средствами

Стоит отметить, что мы с вами разобрали только один самый известный метод решения ОДУ с разными порядками. Однако, методов очень много.

Для решения дифференциальных уравнений и систем в MATLAB предусмотрены следующие функции:

ode45 (f, interval, X0, [options])
ode23 (f, interval, X0, [options])
ode113 (f, interval, X0, [options])
ode15s (f, interval, X0, [options])
ode23s (f, interval, X0, [options])
ode23t (f, interval, X0, [options])
ode23tb (f, interval, X0, [options])

Входными параметрами этих функций являются:

• f — вектор-функция для вычисления правой части уравнения системы уравнений;
• interval — массив из двух чисел, определяющий интервал интегрирования дифференциального уравнения или системы;
• Х0 — вектор начальных условий системы дифференциальных уравнений;
• options — параметры управления ходом решения дифференциального уравнения или системы.

Все функции возвращают:

• массив Т — координаты узлов сетки, в которых ищется решение;
• матрицу X, i-й столбец которой является значением вектор-функции решения в узле Тi.

В функции ode45 реализован метод Рунге-Кутта 4-5 порядка точности, в функции ode23 также реализован метод Рунге-Кутта, но 2-3 порядка, а функция ode113 реализует метод Адамса.

Для решения жёстких систем предназначены функция ode15s, в которой реализован метод Гира, и функция ode23s, реализующая метод Розенброка. Для получения более точного решения жёсткой системы лучше использовать функцию ode15s. Для решения системы с небольшим числом жёсткости можно использовать функцию ode23t, а для грубой оценки подобных систем служит функция ode23tb.

Символьное решение обыкновенных дифференциальных уравнений произвольного порядка осуществляет функция dsolve r = dsolve(‘eq1,eq2,…’, ‘cond1,cond2,…‘, ‘v’)
Пример использования:

На этом мы закончим. Если остались вопросы, задавайте их в комментариях. Также вы можете скачать исходники чтобы лучше понять тему: «Решение ОДУ в Matlab».

Matlab решение дифференциальных уравнений 2 порядка

3 -е занятие по MATLAB

ЛАБОРАТОРНАЯ РАБОТА №3

Трехмерная графика в MATLAB .

Решение обыкновенных дифференциальных уравнений в MATLAB .

1. Элементарная трехмерная (3- D ) графика — функция plot 3.

Функция plot 3 в определенном смысле является аналогом функции plot . С помощью plot 3 формируется построение линии в трехмерном пространстве по заданным трем векторам .

Пример 1.1. Построение трехмерной пространственной спирали.

t =0:0.05:9* pi ; x =2* sin ( t ); y = cos ( t ); % t , x , y — вектора одинакового размера

xlabel( ‘о сь X’ ),ylabel( ‘ось Y’ ),zlabel( ‘ось Z-t’ )

title(‘ Пространственная спираль ‘)

% Сохранить программу в текстовом редакторе MATLAB, например, под именем sp3

% Поменять местами x, y, t в функции plot3

% Сменить начертание и цвет графика

% Добавить пояснение к начертанию в виде легенды — legend( ‘ звездочки ‘ )

%Установить следующий диапазон для t: t=-9*pi:0.05:9*pi;

% Пояснения к графику с помощью функций gtext для 3D-графики не применяются

Пример 1.2. Построение сферы по окружностям.

n=input(‘n=’); % Клавиатурный ввод числа n по запросу в командном окне

t2=(pi/2)*(-n:5:n)’/n ; % транспонированный вектор

E=ones(size(t1)); % матрица единиц размерности вектора t1

% Сохранить программу в текстовом редакторе MATLAB под именем sfera3 .

% Программу выполнить при различных значениях n .

% При n =100 изменить шаг в массивах t1 и t2 : для t1 и t2 одновременно: 3, 1, 10, 25, 50

% Для t1=50, для t2=1; для t1=1, для t2=50.

% Программу sfera3 выполнить без клавиатурного ввода, а для заданного числа n .

% Установить в программе различные цвета изображения сферы.

% Использовать различные коэффициенты для t1 и t2: pi/5, pi/10, pi/50, 2*pi, 5*pi одновременно

% и в сочетании с коэффициентом, равным pi (3.14), при одном из векторов ( t1 или t2).

2. Формирование прямоугольной сетки на плоскости — meshgrid .

% Результатом действия функции meshgrid является формирование «основания» в плоскости XOY для построения над этим основанием пространственной фигуры.

3. Построение пространственных сетчатых фигур — mesh.

Z = 1*x.* exp(-x.^2 — y.^2); % Коэффициент 1 заменить: 2, 5, 10, 20

% Для сравнения применить plot3(x,y,Z),grid вместо mesh(Z) .

R=sqrt(x.^2+y.^2)+0.001; %Коэфф. 0.001 введен для исключения деления на ноль

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

% Для сравнения применить plot3(x,y,Z),grid

4. Сетчатая поверхность с проекциями линий постоянного уровня — meshс.

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

5. Сетчатая поверхность с пьедесталом плоскости отсчета на нулевом уровне— meshz.

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

6. Построение пространственных сплошных фигур — surf.

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

1. С плошная поверхность с проекциями линий постоянного уровня — surfс.

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

8. Стандартные сферические поверхности — sphere .

8 .1. Сфера единичного радиуса — sphere ;

» sphere % равносильно sphere(20);

8.2 Формирование сферы с произвольным радиусом, например, равным 5;

% Выполнить построения с надписями

9. Пространственное распределение вероятностей Гаусса — peaks.

peaks; % По умолчанию формируются матрицы размера 49 ´ 49, по которым строится

%поверхность с пометками координат и титульной надписью ‘Peaks’.

peaks, title(‘Gauss’); % Со специальной титульной надписью

peaks(78); % Размерность матриц построения 78 ´ 78

peaks(25); % Размерность матриц построения 25 ´ 25

z=peaks; surf(z); % Построение поверхности Гаусса по заданной 49 ´ 49 матрице z.

% Сравнить с поверхностью на основе функции mesh(z)

% Сравнить с функцией mesh(z)

z=3*peaks(78); surf(z), title(‘Gauss’) % С множителем по оси Z .

% Применить множители: 4, 10, 33, 50

Пример 9.3. Цветовые массивные уровни на плоскости от распределения Гаусса.

[X,Y,Z]=peaks; pcolor(7*X,12*Y,20*Z),title(‘Цвет’) % С расширенной %областью определения на плоскости XOY — множители 7 и 12 и с изменением по Z — коэф-

Пример 9.4. Распределение Гаусса с задаваемой областью определения на плоскости XOY.

% Функция pcolor позволяет наблюдать обл а сть определения в плоскости XOY

% Изменить шаг по x и y : 0.2, 0.1, 0.5

% Изменить границы по x и y одновременно и порознь :(-7:0.2:3),(-7:0.2:1),(-7:0.2:-1),(-7:0.2:-3)

Пример 9.5. Линии уровня трехмерной поверхности — contour.

% Линии уровня без учета масштаба плоскости XOY:

contour(peaks),grid,title(‘ Линии уровня ‘) % 10 линий уровня по умолчанию

contour(peaks,4),grid,title(‘ Линии уровня ‘) % 4 линии уровня

contour(peaks,10),grid,title(‘ Линии уровня ‘) % 10 лини q уровня

contour(peaks,15),grid,title(‘ Линии уровня ‘) % 15 лини q уровня

contour(peaks,25),grid,title(‘ Линии уровня ‘) % 25 лини q уровня

% Применить функцию contour для стандартной сферической поверхности sphere с различным числом линий уровня.

Пример 9.6. Линии уровня с учетом масштаба плоскости XOY (два примера):

Пример 9.7. Линии уровня с учетом масштаба плоскости XOY и заданным числом (три примера):

Пример 9.7. Линии уровня с цветовой окраской плоскости XOY — contourF.

contourF(peaks),title(‘Цвет линий уровня’)

Пример 9.8. «Пространственные» линии уровня — contour3.

contour3(peaks,25),title(’25 л иний уровня в пространстве ‘)

Пример 9.9. Обзор поверхности из заданной точки пространства — view.

peaks,view(10,45); % Число 10 — азимут обзора, 45 — угол обзора (все в градусах)

[X,Y]=meshgrid(-7:0.3:7,-5:0.3:5);Z=peaks(X,Y);surf(Z), view( — 10,45)

% Задать различные параметры функции view и выполнить построение различных поверхностей.

10. Пострение поверхностей относительно полярной системы координат.

Z=peaks(x1,y1);surf(x1,y1,Z),title(‘ Полярная плоскость ‘)

% С изменением точки обзора

Z=peaks(x1,y1);surf(x1,y1,Z),title(‘ Полярная плоскость ‘),view(-12,45)

11. Построение цилиндрических поверхностей — cylinder.

cylinder % Построение цилиндра без параметров, по умолчанию

cylinder(40) % Построение цилиндра с заданным размером плоскости XOY

cylinder(40,60) % Цилиндр с заданным размером плоскости XOY и числом образующих %граней — 60

% Построение совокупности цилиндрообразующих поверхностей

[x,y,z]=cylinder([5 0],160); surf(x,y,z) % Конус по заданному вектору [5,0]

[x,y,z]=cylinder([5 0 5],160); surf(x,y,z) % 2 к онуса

[x,y,z]=cylinder([5 0],3); surf(x,y,z) % Пирамида

[x,y,z]=cylinder([5 0 5],3); surf(x,y,z) % 2 пиирамиды

[x,y,z]=cylinder([5 12 12],100); surf(x,y,z)

[x,y,z]=cylinder([5 12 5],100); surf(x,y,z)

[x,y,z]=cylinder([5 12 12 5],100); surf(x,y,z)

[x,y,z]=cylinder([5 12 5 12 5 12],100); surf(x,y,z)

[x,y,z]=cylinder([5 12 12 5 18],100); surf(x,y,z)

[x,y,z]=cylinder([5 12 12 5 5 18 18],100); surf(x,y,z)

% Построение совокупности цилиндрообразующих поверхностей с масштабированием

[x,y,z]=cylinder([5 12 12 5 5 18 18],100); surf(x,y,20*z)

plot(x,20*z),grid % Масштаб плоскости XOZ

plot(7*x,y),grid % Масштаб плоскости XOY

plot(7*x,13*y),grid % Масштаб плоскости XOY

Решение обыкновенных дифференциальных уравнений в MATLAB.

Для решения обыкновенных дифференциальных уравнений (ODE) могут быть применены численные методы, которые в MATLAB реализованы в специальных функциях-решателях: ode45, ode23, ode113 .

Общий порядок программирования:

1) Создается М-функция с описанием правых частей дифференциальных уравнений;

2) Создается М-сценарий с выбранным решателем;

Пример 1. Решить следующую систему обыкновенных дифференциальных уравнений с заданными начальными условиями:

% Программа решения примера 1

% Создаем М-функцию под именем dif31.m

% Создаем М-сценарий под именем ddd45_31.m

% Сценарий решения с помощью ode45

T=[0 15]; % Интервал интегрирования

x0=[10;5]; % Начальные условия

[t,x]=ode45(‘dif31’,T,x0); %t, x — выходные переменные решателя ode45

plot(t,x),grid,title(‘ Пример 3.1 ‘),legend(‘X1′,’X2’)

% Изменить начальные условия:

% Изменить интервал интегрирования: от 0 до 20, от 0 до 7.

% Вывести графические результаты с различным начертанием координат

% Прменить решатели ode23, ode113 . Сравнить результаты покоординатно, для чего вывести результаты решения и свести их в таблицу, например, в WORD .

Пример 2. Решить следующую систему линейных дифференциальных уравнений с заданными начальными условиями:

% Создаем М-функцию с именем dif32.m

function f=dif32(t,x); % t, x — входные переменные для М-функции

%Создаем М-сценарий под именем ddd45_32

% Сценарий решения примера 2

x0=[0;0;0]; % x0 — вектор начальных условий

% Изменить интервал интегрирования

% Изменить начальные условия

% Вывести графические результаты с различным начертанием координат

% Использовать решатели ode23, ode113 .

Пример 3. Уравнение Ван-дер-Поля.

Для решения дифференциального уравнения 2-го порядка сначала приведем его к системе дифференциальных уравнений 1-го порядка:

где

% Создаем М-функцию под именем van33.m

%Создаем М-сценарий под именем ddd45_33

plot(t,X),grid,title(‘ Ур-е Ван-дер-Поля ‘ ), legend(‘X1′,’X2’)

% Изменить интервал интегрирования

% Изменить начальные условия ( только все нулевые не должны быть)

% Изменить множитель в уравнении (вместо 2)

% Вывести графические результаты с различным начертанием координат

% Использовать решатели ode23, ode113 .

Пример 4. Интегрирование дифференциальных уравнений с выводом результатов в заданн ом диапазоне точек независимого переменного. Видоизменим пример 2 в сценарии задания интервала интегрирования.

% Сценарий решения примера 4

T=[0:1:6,7:2:18]; % от 0 до 6 шаг 1, от 7 до 18 шаг 2

Пример 5. Интегрирование дифференциальных уравнений с выводом результатов в заданных точках независимого переменного. Видоизменим пример 2 в сценарии задания интервала интегрирования.

% Сценарий решения примера 5

T=[0 0.5 1 1.5 3 4 8]; 7 точек переменного t

Задание к примерам 1-5: произвести графический вывод координат каждой в отдельности

Пример 6. Интегрирование систем линейных дифференциальных уравнений в матричном виде, т.е.

(6.1)

где — вектор переменных состояния размера n ´ 1, — вектор входного воздействия размера rx1, — матрицы чисел размера n ´ n, n ´ r, соответственно .

% Матрицы и берем из примера 2

% Создаем М-функцию под именем syst36.m

A=[-3,0,0;1,-2,0;0,4,-1]; % Матрица А размера 3 ´ 3

B=[10 0 0;0 0 0;0 0 0]; % Матрица B размера 3 ´ 3

u=[1;1;1]; % Входное воздействие размера 3 ´ 1

ds36=A*x+B*u; % Описание правой части матричного дифференциального уравнения (6.1)

% Создаем М-сценарий под именем ddd45_36

% Сценарий решения примера 3.6

plot(t,x),grid,title(‘ Система ур-й 3-го порядка ‘),

Задание к примеру 6:

% Решить систему с двумя воздействиями, с одним воздействием

% Вывести графические результаты с различным начертанием координат

% Вывести графические результаты с по отдельным координатам

% Создать программу решения системы дифференциальных уравнений 4-го порядка

% Использовать решатели ode23, ode113 .

Решение обыкновенных дифференциальных уравнений

с заданной точностью и с параметрами.

Решатели дифференциальных уравнений по умолчанию производят численное интегрирование с относительной погрешностью и вектором абсолютной погрешности со значением по всем компонентам вектора.

1. Установление заданной относительной погрешности RelTol — ODESET( odeset) .

С помощью установления относительной погрешности RelTol контролируется количество «правильных» цифр в решении дифференциального уравнения в соответствии с общей записью , где показатель степени P есть число контролируемых цифр в решении.

Пример1. Уравнение Ван-дер-Поля с заданной относительной погрешностью.

С помощью функции ODESET задаются опции решателя дифуравнений с помощью соответствующих строковых символов, которых всего может быть 18. Перечень строковых символов функции ODESET можно просмотреть из командной строки, набрав в ней ODESET

% Сформируем М-функцию для описания правых частей дифференциальных уравнений

% Сохрани ть под именем van33

% Создадим М-сценарий решения на основе ode23 и с относительной погрешностью, равной

% d1= 0.1 и d2=0.0001

% М-сценарий сохранить под именем ret71.

% Формат записи функции odeset включает строковый служебный символ RelTol и задаваемую %величину относительной погрешности (0.1 для d1 и 0.2 для d2).

% d1 и d2 подставляются в соответствующие решатели ( ode23).

Задание к примеру 1:

— выполнить с ode45, ode113;

— изменить коэффициент в М-функции van33 : 0.3, 2.3;

— изменить для d1 относительную погрешность: 1, 0.5, 0.1, 0.01, 0.001, 0.0001 (для ode23).

Пример 2. Анализ нелинейной тест-системы с задаваемой относительной погрешностью вычислений в решателях MATLAB.

где — постоянные действительные числа.

2.1. Проинтегрируем тест-систему с коэффициентами и с относительной погрешностью, равной 0.1, 0.01, 0.001, 0.4, 0.3, 0.2

% Создадим М-функцию под именем dif21

% Создадим М-сценарий под именем syst21

% Введем относительную погрешность 0.1

% В сценарии применим функцию odeset

% Проанализировать тест-систему по 2-й и 3-й координатам.

% Для графического вывода результатов по 2-й координате следует ввести plot в виде

%% Для графического вывода результатов по 3-й координате следует ввести plot в виде

% Проанализировать тест-систему с относительной погрешностью, равной 0.01, 0.4, 0.3, 0.2

% Проанализировать тест-систему с помощью решателей ode45, ode113 , сравнить результаты.

2. Задание абсолютной погрешности — AbsTol .

Абсолютная погрешность AbsTol контролирует разницу между ожидаемым решением и его действительным значением. AbsTol начинает проявляться, когда компонента (координата) решения становится неожидаемо большой. Влияние AbsTol зависит также от интервала и масштаба интегрирования. По умолчанию решатели дифференциальных уравнений Matlab устанавливают величину абсолютной погрешности, равную .

Пример3. Уравнение Ван-дер-Поля с заданной абсолютной погрешностью — ‘AbsTol’ .

% Используем имеющую М-функцию описания уравнения Ван-дер-Поля — van33

% Создадим М-сценарий ( присвоить имя) с задаваемой абсолютной погрешностью по всем координатам и по %одной из возможных

a1=odeset(‘AbsTol’,0.5); % Скаляр 0.1 по всем координатам

% Задание избирательной абсолютной погрешности осуществляется с помощью вектора в виде :

% По первой координате погрешность равна 0.5, по 2-й — 0.000001

% В целом сценарий (присвоить имя) должен иметь вид

% Поскольку система уравнений Ван-дер-Поля имеет взаимозависимые координаты, то интегрирование осуществляется практически с наименьшей погрешностью, т.е. с 0.000001

Задание к примеру 3.

— Применить скаляр абсолютной погрешности: 0.3, 0.1, 0.01.

— Вывести график по 2-й координате.

3. Интегрирование дифференциальных уравнений с параметрами.

Пример 4. Проинтегрировать однородную систему нелинейных дифференциальных уравнений с четырьмя параметрами k1, k2, k3, a:

при следующих начальных условиях:

Целью является анализ решений при различных параметрах, входящих в систему.

% Создадим М-функцию под именем dif44 с ключевым словом flag

switch flag % Начало процедуры описания правых частей дифуравнений

case » % Состояние flag с опциями по умолчанию

end % Окончание описания правых частей дифуравнений с опциями по умолчанию

% Создадим М-сценарий под именем syst44 для решателя ode23 c опциями по умолчанию

% и введения параметров

x0=[0;1;-1]; % Вектор начальных условий

tt=[0,25]; % Интервал интегрирования

k1=input(‘k1=’)%2.333; % Можно также k1=2.333;

k2=input(‘k2=’)%-0.7789; % Можно также k2=-0.7789;

k3=input(‘k3=’)%-0.7888; % Можно также k3=-0.7888;

a=input(‘a=’)%-0.1; % Можно также a=-0.1;

plot(t,x),grid,title(‘ Система с параметрами ‘), legend( ‘x1’ , ‘x2’ , ‘x3’ )

% В записи функции ode23 символ [ ] указывает на опции ( RelTol, AbsTol и др.), принятые по %умолчанию

Задание к примеру 4.

— Изменить параметр k1: 2, 1, 0.5, 0.2; ( остальные исходные) ;

— Изменить параметр k2: -0.111, -0.333,-0.555,0.7789 ( остальные исходные) ;

— Изменить параметр k3: -1.333, -0.333, -0.666, 0.7888 ( остальные исходные) ;

— Изменить параметр a: -1, 1, 0, 0.5 ( остальные исходные) ;

Произвести интегрирование системы при:

Пример 5. Интегрирование систем с циклическим изменением параметра.

% Используем М-функцию dif55

% Видоизменим М-сценарий syst66 так, чтобы программно изменялся какой-либо параметр (например, k3) и происходило наложение графиков решения по заданной координате (например, по ). Новый М-сценарий будет с именем syst77.

if i==-0.51 % Двойное равенство соответствует логической истине

plot(t,x(:,2),’r’),title(‘ Система с циклическим параметром ‘ )

k3=i; % Без точки с запятой (;) выводятся значения k3

Задание к примеру 5.

— Расширить диапазон изменения параметра k3;

— Написать программу с изменением параметра k2 ;

— Написать программу с графическим выводом всех координат системы при k3=0.51 и только координаты при остальных значениях параметра k3 .

Matlab решение дифференциальных уравнений 2 порядка

Дифференциальные уравнения и системы уравнений

Для решения дифференциальных уравнений и систем в MATLAB предусмотрены следующие функции ode45(f, interval, X0 [, options]), ode23(f, interval, X0 [, options]), ode113(f, interval, X0 [, options]), odel5s(f, interval, X0 [, options]), ode23s(f, interval, X0 [, options]), ode23t (f, interval, X0 [,options]) и ode23tb(f, interval, X0 [, options]).

Входными параметрами этих функций являются:

• f — вектор-функция для вычисления правой части уравнения системы уравнений
• interval — массив из двух чисел, определяющий интервал интегрирования дифференциального уравнения или системы;
• Х0 — вектор начальных условий системы дифференциальных систем
• options — параметры управления ходом решения дифференциального уравнения или системы.

Все функции возвращают:

• массив Т — координаты узлов сетки, в которых ищется решение;
• матрицу X, i-й столбец которой является значением вектор-функции решения в узле Тi

В функции ode45 реализован метод Рунге-Кутта 4-5 порядка точности, в функции ode23 также реализован метод Рунге-Кутта, но 2-3 порядка, а функция ode113 реализует метод Адамса.

В М-файле с именем pr 7. m пишем:

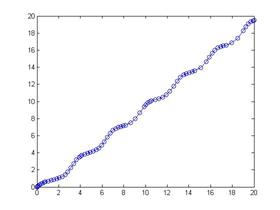
Потом в командном окне вызываем функцию ode113:

ode113(@pr7,[0 20],0) %Метод Адамса: @ pr 7 – ссылка на М-функцию, [0 20]- интервалы интегрирования,0 — условие: y(0)=0

Результатом будет график:

Необходимо реализовать метод Рунге-Кутта 4 порядка и решить задачу Коши для предложенной системы дифференциальных уравнений:

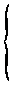
В М-файле с именем pr 8. m пишем:

Потом в командном окне вызываем функцию ode 45: