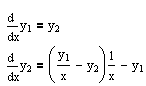Matlab решение систем дифференциальных уравнений

Matlab решение систем дифференциальных уравнений

Дифференциальные уравнения и системы уравнений

Для решения дифференциальных уравнений и систем в MATLAB предусмотрены следующие функции ode45(f, interval, X0 [, options]), ode23(f, interval, X0 [, options]), ode113(f, interval, X0 [, options]), odel5s(f, interval, X0 [, options]), ode23s(f, interval, X0 [, options]), ode23t (f, interval, X0 [,options]) и ode23tb(f, interval, X0 [, options]).

Входными параметрами этих функций являются:

• f — вектор-функция для вычисления правой части уравнения системы уравнений
• interval — массив из двух чисел, определяющий интервал интегрирования дифференциального уравнения или системы;
• Х0 — вектор начальных условий системы дифференциальных систем
• options — параметры управления ходом решения дифференциального уравнения или системы.

Все функции возвращают:

• массив Т — координаты узлов сетки, в которых ищется решение;
• матрицу X, i-й столбец которой является значением вектор-функции решения в узле Тi

В функции ode45 реализован метод Рунге-Кутта 4-5 порядка точности, в функции ode23 также реализован метод Рунге-Кутта, но 2-3 порядка, а функция ode113 реализует метод Адамса.

В М-файле с именем pr 7. m пишем:

Потом в командном окне вызываем функцию ode113:

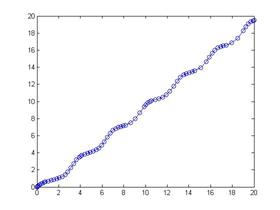
ode113(@pr7,[0 20],0) %Метод Адамса: @ pr 7 – ссылка на М-функцию, [0 20]- интервалы интегрирования,0 — условие: y(0)=0

Результатом будет график:

Необходимо реализовать метод Рунге-Кутта 4 порядка и решить задачу Коши для предложенной системы дифференциальных уравнений:

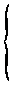
В М-файле с именем pr 8. m пишем:

Потом в командном окне вызываем функцию ode 45:

Решение ОДУ в Matlab

Доброго времени суток! Сегодня мы поговорим о решении ОДУ (обыкновенных дифференциальных уравнений) в Matlab. Перед тем как мы начнём обсуждать данную тему, советую вам ознакомиться с темой: Численное дифференцирование в Matlab, чтобы лучше понимать теоретическую составляющую решения ОДУ.

Обыкновенные дифференциальные уравнения

С помощью дифференциальных уравнений можно описать разные задачи: движения системы, взаимодействующих материальных точек, химической кинетики и т.д. Различают три типа задач для систем диф. уравнений:

• Задача Коши
• Краевая задача
• Задача на собственные значения

Кратко расскажу о их сути:

Задача Коши предполагает дополнительные условия в виде значения функции в определённой точке.
Краевая задача подразумевает поиск решения на заданном отрезке с краевыми (граничными) условиями в концах интервала или на границе области.
Задача на собственные значения — помимо искомых функций и их производных, в уравнение входят дополнительное несколько неизвестных параметров, которые являются собственными значениями.

Методы решения дифференциальных уравнений

Решение ОДУ в Matlab и не только, в первую очередь, сводится к выбору порядка численного метода решения. Порядок численного метода не связан с порядком дифференциального уравнения. Высокий порядок у численного метода означает его скорость сходимости.

В случае большого интервала, с помощью алгоритмов с низким порядком сжимают интервал с решениями и находят приблизительные корни, а затем уже уточняют корни с помощью методов с высоким порядком.

Решение обыкновенных дифференциальных уравнений в Matlab можно реализовать «своими ручками», прописав алгоритм по разным схемам. Но также в Matlab есть встроенные функции, выполняющие все стандартные задачи.

Метод Рунге-Кутта первого порядка

Методы Рунге-Кутта представляют собой разложения в ряд Тейлора и от количества использованных элементов ряда зависит порядок этого метода. Следовательно, помимо Рунге-Кутта первого порядка, вы сможете увидеть методы других порядков. Иногда их называют другими именами.

Например, Метод Рунге-Кутта первого порядка, также известен как Метод Эйлера или Метод ломаных. Информацию о его математическом и графическом представлении советую поискать в гугл. Мы же поговорим о том, как Метод Рунге-Кутта первого порядка реализуется в Matlab для решения ОДУ. Например:

Решить и привести график ошибки уравнения y’ = y*x методом Рунге-Кутта первого порядка (Методом Эйлера, Методом ломаных).

Погрешность Метода Рунге-Кутта 1 порядка

» data-medium-file=»https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/Рунге-1-погрешность.png?fit=300%2C236&ssl=1″ data-large-file=»https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/Рунге-1-погрешность.png?fit=622%2C489&ssl=1″ loading=»lazy» src=»https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/%D0%A0%D1%83%D0%BD%D0%B3%D0%B5-1-%D0%BF%D0%BE%D0%B3%D1%80%D0%B5%D1%88%D0%BD%D0%BE%D1%81%D1%82%D1%8C.png?resize=622%2C489″ alt=»Погрешность метода 1 порядка» width=»622″ height=»489″ srcset=»https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/Рунге-1-погрешность.png?w=629&ssl=1 629w, https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/Рунге-1-погрешность.png?resize=300%2C236&ssl=1 300w» sizes=»(max-width: 622px) 100vw, 622px» data-recalc-dims=»1″ />
На данном графике показана зависимость величины ошибки от шага.

Метод Рунге-Кутта второго порядка

Также известен как Метод Эйлера-Коши. Как видите, во второй части уравнения происходит обращения к следующему шагу. Но как тогда быть, если нам ещё не известен следующий шаг? Всё просто. Метод Рунге-Кутта второго порядка — это всё тот же метод первого порядка, однако, на половине шага происходит нахождение «первичного» решения, а затем происходит его уточнение. Это позволяет поднять порядок скорости сходимости до двух.

Решить и привести график ошибки уравнения u’ = u*x методом Рунге-Кутта второго порядка.

По сравнению с Рунге-Куттом первого порядка изначальная ошибка уже гораздо меньше.

Мы не будем говорить о третьем порядке, потому что задачи на третий порядок встречаются редко, но если будет необходимо, пишите в комментариях, выложу.

Метод Рунге-Кутта четвёртого порядка

Метод Рунге-Кутта четвёртого порядка считается самым распространённым. Тем не менее, работает он аналогично второму и третьему порядку.

Решить и привести график ошибки уравнения u’ = u*x методом Рунге-Кутта четвёртого порядка.

Как видите, на последней картинке размерность ошибки на столько мала, что пришлось воспользоваться loglog() для лучшей видимости.

Решение ОДУ в Matlab стандартными средствами

Стоит отметить, что мы с вами разобрали только один самый известный метод решения ОДУ с разными порядками. Однако, методов очень много.

Для решения дифференциальных уравнений и систем в MATLAB предусмотрены следующие функции:

ode45 (f, interval, X0, [options])
ode23 (f, interval, X0, [options])
ode113 (f, interval, X0, [options])
ode15s (f, interval, X0, [options])
ode23s (f, interval, X0, [options])
ode23t (f, interval, X0, [options])
ode23tb (f, interval, X0, [options])

Входными параметрами этих функций являются:

• f — вектор-функция для вычисления правой части уравнения системы уравнений;
• interval — массив из двух чисел, определяющий интервал интегрирования дифференциального уравнения или системы;
• Х0 — вектор начальных условий системы дифференциальных уравнений;
• options — параметры управления ходом решения дифференциального уравнения или системы.

Все функции возвращают:

• массив Т — координаты узлов сетки, в которых ищется решение;
• матрицу X, i-й столбец которой является значением вектор-функции решения в узле Тi.

В функции ode45 реализован метод Рунге-Кутта 4-5 порядка точности, в функции ode23 также реализован метод Рунге-Кутта, но 2-3 порядка, а функция ode113 реализует метод Адамса.

Для решения жёстких систем предназначены функция ode15s, в которой реализован метод Гира, и функция ode23s, реализующая метод Розенброка. Для получения более точного решения жёсткой системы лучше использовать функцию ode15s. Для решения системы с небольшим числом жёсткости можно использовать функцию ode23t, а для грубой оценки подобных систем служит функция ode23tb.

Символьное решение обыкновенных дифференциальных уравнений произвольного порядка осуществляет функция dsolve r = dsolve(‘eq1,eq2,…’, ‘cond1,cond2,…‘, ‘v’)
Пример использования:

На этом мы закончим. Если остались вопросы, задавайте их в комментариях. Также вы можете скачать исходники чтобы лучше понять тему: «Решение ОДУ в Matlab».

Решение систем дифференциальных уравнений в MATLAB

Решение систем дифференциальных уравнений.

Для решения систем дифференциальных уравнений существует несколько встроенных процедур. Рассмотрим применение процедуры ode45. Как один из возможных форматов вызова, можно предложить такой: [t,r]=ode45(@DiffEquationFunction,[Tstart,Tfinish], StartVector). Отметим, что процедура ode45 может решить систему уравнений следующего вида: , где — есть векторная функция .

Рассмотрим пример, иллюстрирующий создание исходной функции DiffEquationFunction для вызова ее процедурой ode45. Пусть некоторая точка массы движется в гравитационном поле неподвижных точек с массами и (см. рис.). Уравнение сил в гравитационном поле точек и будет следующим: . Как видим, данное дифференциальное уравнение имеет второй порядок. Но его можно свести к системе дифференциальных уравнений первого порядка: .

Будем считать, что данная задача является «плоской» и введем следующие обозначения: , , и . Исходя из таких обозначений, систему дифференциальных уравнений движения точки в гравитационном поле можно представить следующим образом: .

Без ущерба для сути решения, значение гравитационной постоянной примем равной 1, , , , .

В таком виде систему уравнений можно уже записать как файл-функцию, что мы и сделали, назвав ее threepoint(t,x).

M1=50; M2=0; C1x=5; C1y=0; C2x=0; C2y=10;

Решим систему дифференциальных уравнений, вызвав процедуру ode45 из файла-функции dynpoint.m.

x1=5; y1=0; x2=0; y2=10;

При таких начальных параметрах ( ) наша точка движется в поле одного объекта.

То, что мы получили вполне можно назвать приемлемым результатом. Нашей целью являлась корректная подготовка системы дифференциальных уравнений для ее решения процедурой ode45. С другой стороны, применяя иные встроенные процедуры можно получить отличающиеся в корне результаты.

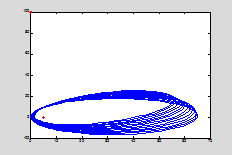
Попробуем немного поэкспериментировать и введем значение . Это должно внести возмущения в орбиту движущейся точки.

Крестиком и звездочкой на графике отмечены соответственно и . Помимо процедуры ode45 существует еще ряд встроенных процедур решения систем дифференциальных уравнений. Их описание можно найти в книгах, указанных в списке литературы. Поскольку, решение систем дифференциальных уравнений является очень важным моментом, то мы не ограничимся одним примером.

Рассмотрим следующую задачу, опять же из физики. Рассмотрим траекторию движения пули под действием силы тяжести. При отсутствии сопротивления воздуха, как известно из курса средней школы, это будет парабола. Мы же рассмотрим случай, когда сила сопротивления воздуха пропорциональна квадрату скорости и противоположна направлению движения. Как говорит школьный курс физики, уравнение баланса сил будет следующим: . Учитывая то, что ускорение – производная скорости по времени, распишем это уравнение в векторном виде: . Где — плотность воздуха, — масса пули, — площадь поперечного сечения. Распишем это уравнение покоординатно: . В таком виде система дифференциальных уравнений готова для того, чтобы попытаться решить ее при помощи процедуры ode45. Пусть масса пули – 10 грамм, поперечник – 1 см 2 , плотность воздуха – 1 кг/м 3 . С такими данными мы составим файл-функцию airpoint.m.

g=10; ro=1; s=0.0001; m=0.01; k=ro*s/(2*m);

В такой системе уравнений аргументом являются скорость и время. Если мы хотим найти траекторию движения, то мы должны принять во внимание: . Полученные массивы точек , , можно в дальнейшем обработать. Произвести интерполяцию, аппроксимацию и т.д. Но мы интегрирование заменим суммированием: . В этом случае начальный момент времени равен 0, пуля находится в начале координат. Создадим файл-функцию dynairpoint, в которой вызовем процедуру ode45. В начальный момент времени скорость пули по горизонтали 800, по вертикали – 100.