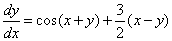Matlab simulink решение дифференциального уравнения

Matlab simulink решение дифференциального уравнения

Дифференциальные уравнения и системы уравнений

Необходимо решить уравнение:

Попробуем решить его с помощью программы Simulink пакета MATLAB.

Метод решения дифференциальных уравнений отличается от традиционного. Нам необходимо создать схему уравнения. Необходимо будет создать обратную связь между выходными значениями интегратора и новым значением переменной. У нашего уравнения линейно изменяется x от 0 до 20. Поэтому для решения уравнения необходимо использовать блок Ramp . В конце обязательно должен быть интегрирующий блок, а из него результат выходит на осциллограф.

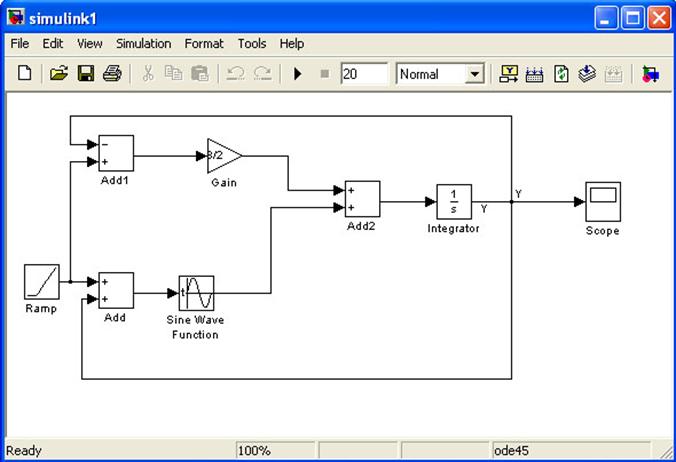
Решение уравнения выглядит так:

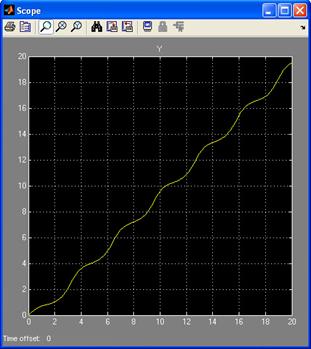
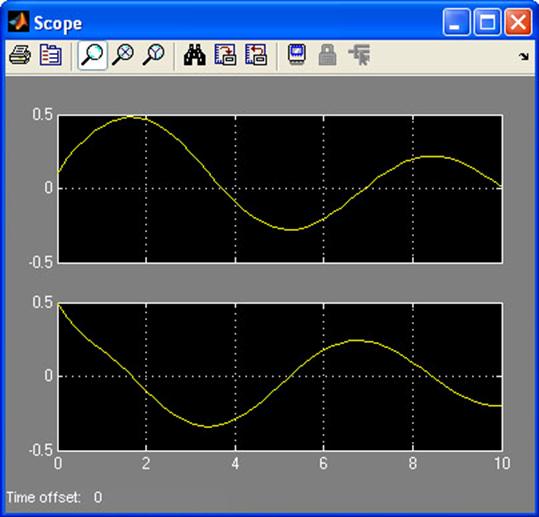
Результатом будет график x от y :

Рассмотрим из каких библиотек взяты использованные блоки.

Ramp – из Sources. Формирует линейный сигнал . В параметрах необходимо задать 1.

Add – Math Operations. В параметрах выбираем необходимые нам операции.

Gain – Math Operations . Коэффициент усиления сигнала. В параметрах ставим значение 3/2.

Sine Wave Function – Sources. Т.к. нам необходим косинус, то в параметрах Phase ставим pi/2.

Integrator – Continuous . Выполняет интегрирование входного сигнала.

Scope – Sinks . Выводим результат – график сигнала в функции времени.

Дифференциальные уравнения 2-го порядка.

Дана система уравнений:

Решим ее с помощью программы Simulink пакета MATLAB.

Решаем аналогично предыдущему случаю.

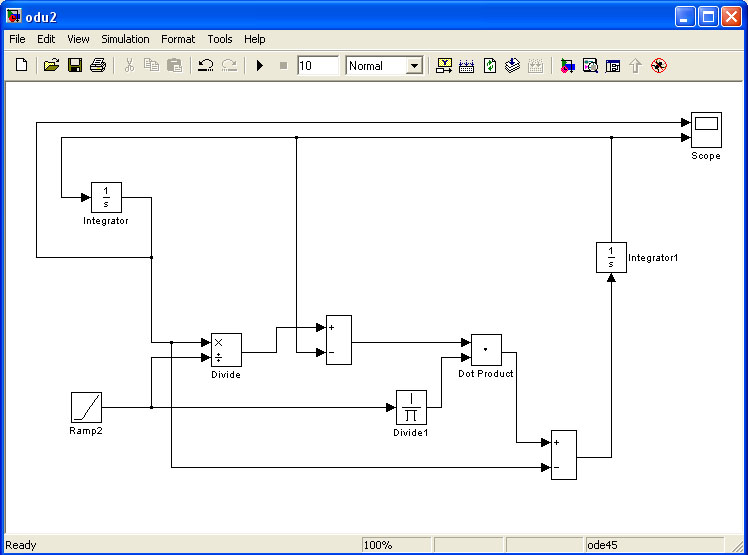
В данной системе уравнений линейно изменяется x от 1 до 10. Также необходимо сделать обратную связь между выходными значениями интеграторов и новым значение переменной x . Обязательно надо в интеграторах задать начальные значения y₁(0) = 0.1; y₂(0) = 0.5.

Результатом будут два графика:

Рассмотрим из каких библиотек взяты использованные блоки.

Ramp – из Sources . Формирует линейный сигнал. В параметрах необходимо задать все значения 1.

Integrator – Continuous . Выполняет интегрирование входного сигнала. Необходимо задать начальные значения Initial condition для y ₁ 0.1, для y ₂ 0.5.

Add – Math Operations . В параметрах выбираем необходимые нам операции.

Divide — Math Operations . Деление первой входной величины на вторую.

Dot Product — Math Operations. Перемножение .

Scope – Sinks. Выводим результат – график сигнала в функции времени.

Решение дифференциального уравнения различными методами, доступными SIMULINK

Страницы работы

Содержание работы

Файл Модели\САМРаботы02\САМ06а.doc 5 стр. 200 Кбайт

1. Решение дифференциального уравнения различными методами, доступными SIMULINK.

Пусть, к примеру, требуется решить линейное дифференциальное уравнение второго порядка с правой частью

. (П7.01)

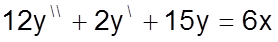
При использовании SIMULINK это уравнение можно решить несколькими способами.

Первый способ решения.

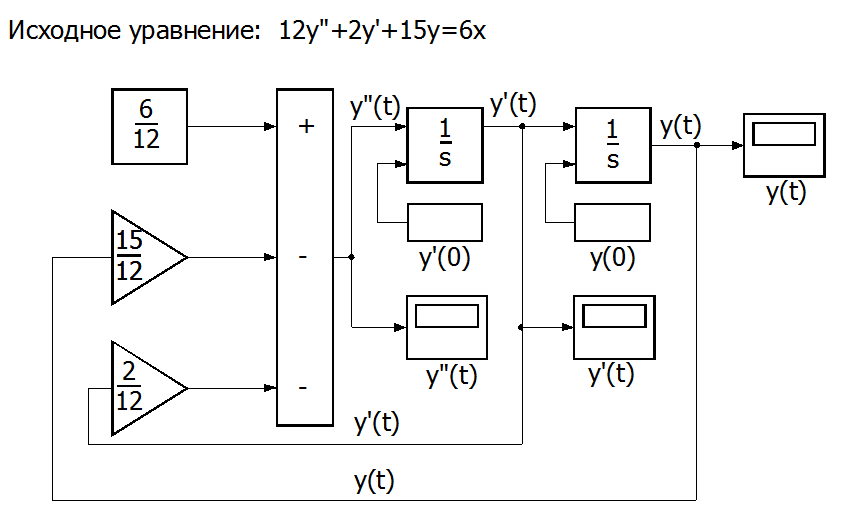
а) Разрабатывается блок-схема решения с использованием в качестве задатчиков коэффициентов уравнения модулей Gain раздела Linear. Начнем с того, что разрешим его относительно второй производной

(П7.02)

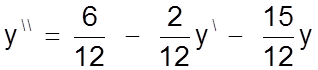
Полученное решение в модулях SIMULINK можно изобразить в виде

Рис. П7.1 Блок-схема решения с использованием в качестве задатчиков коэффициентов уравнения модулей Gain[1].

Для решения уравнения нами использованы 2 интегратора, 1 сумматор и 2 усилителя из раздела Linear библиотеки SIMULINK.

Вторая производная, согласно П7.02, должна получится путем вычитания из y₀ равного 6/12, производных, умноженных на соответствующие коэффициенты.

Вид и значение параметров решения можно наблюдать на экране блока Scope раздела Sinks [siŋks — получатели] «y(t)».

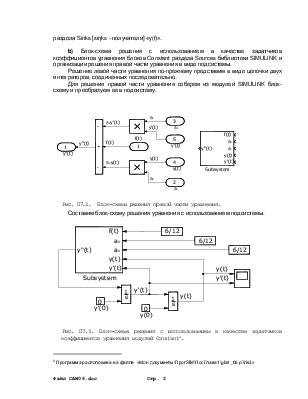
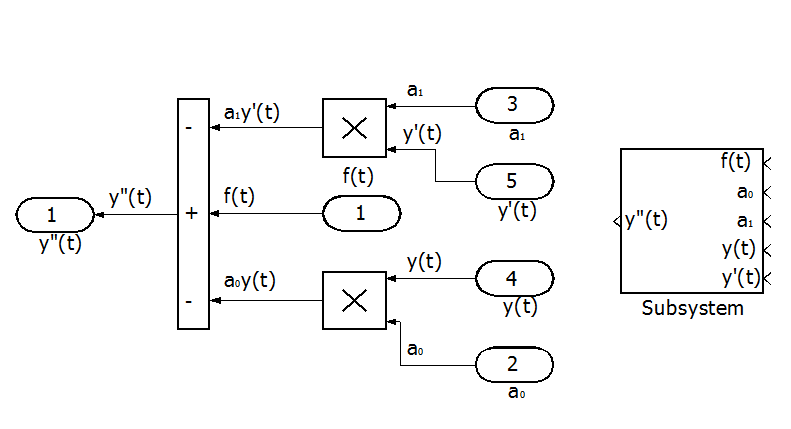
b) Блок-схема решения с использованием в качестве задатчиков коэффициентов уравнения блоков Constant раздела Sources библиотеки SIMULINK и организации решения правой части уравнения в виде подсистемы.

Решение левой части уравнения по-прежнему представим в виде цепочки двух интеграторов, соединенных последовательно.

Для решения правой части уравнения соберем из модулей SIMULINK блок-схему и преобразуем ее в подсистему.

Рис. П7.2. Блок-схема решения правой части уравнения.

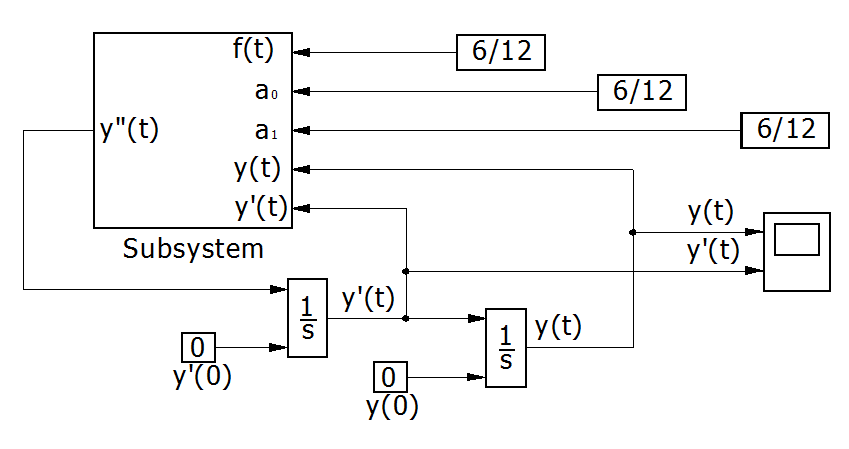
Составим блок-схему решения уравнения с использованием подсистемы.

Рис. П7.3. Блок-схема решения с использованием в качестве задатчиков коэффициентов уравнения модулей Constant[2].

Второй способ решения.

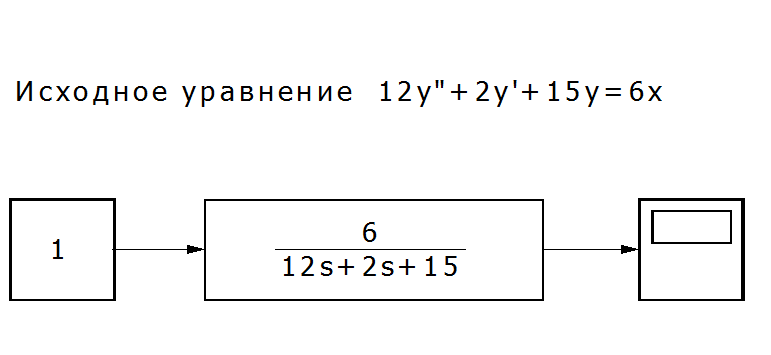
Используя SIMULINK, можно представить другой способ решения этого уравнения. Решение можно получить, используя модуль Transfer Fcn [‘trænsfə: Fkn] (Передаточное звено). В качестве входного сигнала будем использовать блок Constant раздела Sources [so:s — источники]

Рис. П7.4. Решение уравнения с использованием типовых структурных схем[3].

Вид и значение параметров решения можно наблюдать на экране блока Scope раздела Sinks [siŋks — получатели] «Интеграл».

Третий способ решения.

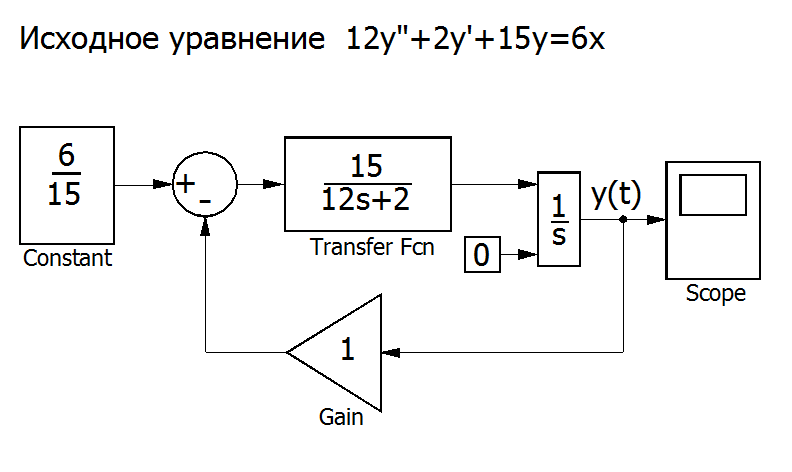
SIMULINK может предложить еще один способ решения данного дифференциального уравнения. Воспользовавшись методами структурных преобразований, данное уравнение можно представить в виде структурной схемы, состоящей из типовых модулей.

Рис. П7.5. Решение уравнения с использованием структурных преобразований[4].

Проведем исследование дифференциального уравнения 2 порядка

(П8.01)

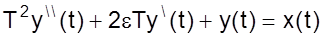
методами фазовой плоскости, используя возможности SIMULINK.

Начнем с того, что разрешим уравнение относительно старшей производной.

(П8.02)

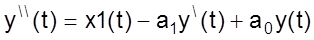
Решение левой части уравнения представим в виде цепочки из двух интеграторов соответственно настроенных.

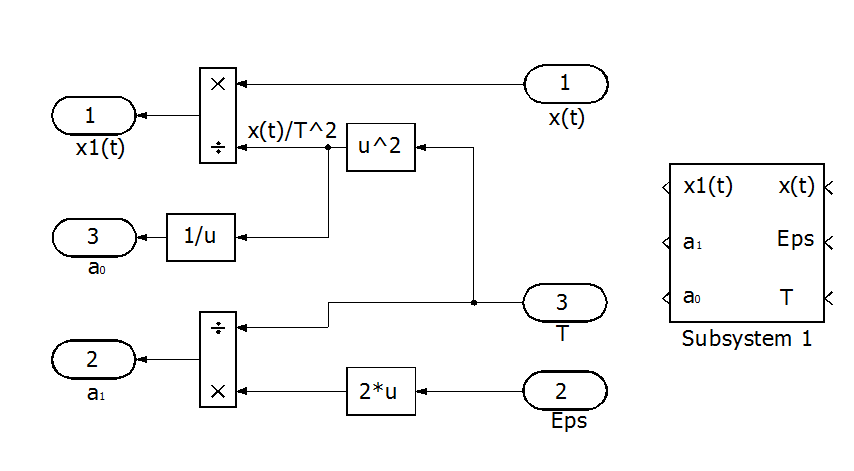
Для решения правой части уравнения создадим 2 подсистемы. Одну для формирования значений коэффициентов уравнения, разрешенного относительно старшей производной и вторую для решения собственно правой части уравнения.

Рис. П8.1 Блок-схема формирования коэффициентов уравнения.

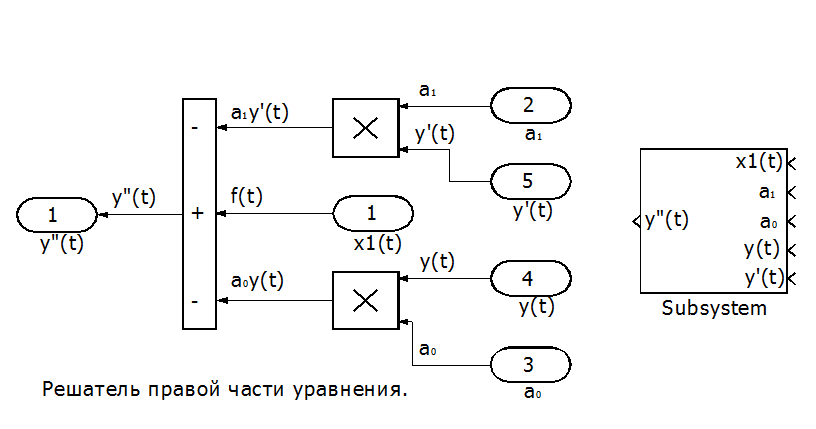
Рис. П8.2. Решатель правой части уравнения.

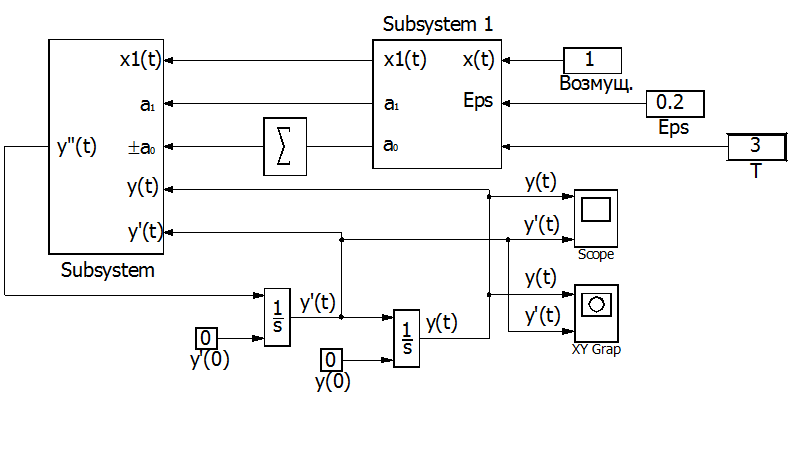
Решение дифференциального уравнения с учетом созданных подсистем будет иметь вид

Рис. П8.3. Блок-схема решения дифференциального уравнения[5].

Исследование фазового портрета.

Для наблюдения за фазовыми траекториями включим в качестве смотрового окна в блок-схему решения уравнения рис. П7.3 дополнительно модуль XY Graph из раздела Sinks библиотеки SIMULINK.

Сущность метода фазовой плоскости заключается в построении фазовых траекторий по дифференциальным уравнениям в системе координат: ось x — значение исследуемой величины u, ось y – скорость ее изменения du/dt. Процесс изменения траектории представляет собой движение изображающей точки на фазовой плоскости. Начальные условия определяют первоначальное положение изображающей точки на фазовой плоскости. Совокупность фазовых траекторий в плоскости (x, y) носит название фазовый портрет. Подробнее с методами фазовой плоскости можно ознакомиться по «Иващенко Н.Н. Автоматическое регулирование. Теория и элементы систем. Учебник для вузов. Изд. 4-е, перераб. и доп. М., «Машиностроение», 1978. Стр. 485-495».

Задачей нашего исследования является построение некоторых наиболее характерных фазовых портретов.

Рассмотрим следующие случаи характерные для уравнения 2 порядка:

[1] Программа расположена на файле «Мои документы\ПрогSIM\ПосГлава1\gla1_06 p7ris1»

[2] Программа расположена на файле «Мои документы\ПрогSIM\ПосГлава1\gla1_06 p7ris3»

[3] Программа расположена на файле «Мои документы\ПрогSIM\ПосГлава1\gla1_06 p7ris4»

[4] Программа расположена на файле «Мои документы\ПрогSIM\ПосГлава1\gla1_06 p7ris5»

[5] Программа расположена на файле «Мои документы\ПрогSIM\ПосГлава1\gla1_06 p8ris3»

Решение систем обыкновенных дифференциальных уравнений в среде MATLAB. Часть 1

В среде MATLAB можно решать системы диффуров с начальными условиями, краевые задачи, а также решать дифференциальные уравнения в частных производных с помощью инструмента PDE toolbox.

В данном обзоре речь пойдет лишь о системах дифференциальных уравнений с начальными условиями, то есть о задаче Коши. В англоязычной литературе это называется Initial Value Problem.

• каким образом записывать системы диффуров
• как задать начальные условия
• временной интервал
• какой получать результат решения для дальнего использования

Решать системы обыкновенных дифференциальных уравнений можно как в MATLAB, так и в Simulink.

В первую очередь, следует определиться, использовать для решения Matlab и его текстовый редактор, или Simulink, где те же системы дифференциальных уравнений могут быть записаны в виде функциональных блоков.

Выбор ваш должен зависеть от задачи. Если Вы, например, хотите смоделировать какой-либо объект управления, описываемый системой диффуров, то в данном случае имеет смысл использовать именно Simulink, так как Вам, впоследствии, понадобиться синтез, например, системы управления, и Simulink подойдет здесь как нельзя лучше.

А вот если у Вас, например, есть необходимость решать системы диффуров с большим количеством уравнений и неизвестных, или специфика Вашей задачи требует особой и специальной настройки численного метода, а также если вы хотите использовать решение диффура в составе других скриптов MATLAB, то Вам имеет смысл решать дифференциальные уравнения способом, о котором пойдёт речь в этом обзоре.

Рассмотрим синтаксис решателей matlab.В качестве аргументов следует подать правую часть системы в виде MATLAB-функции.

На рисунке показан требуемый вид системы, когда выражены старшие производные.

Системы, чей вид отличается от требуемого, следует преобразовать к таковому.

Если функция простая, то её можно записать прямо в поле аргумента, однако, когда речь идёт о системах уравнений, имеет смысл записывать систему уравнений в виде отдельной функции, в том числе и в виде отдельного м-файла. Об этом мы поговорим чуть позже и на конкретном примере.

Также подается интервал времени, на котором будет найдено решение. Интервал задаётся строкой из двух чисел: начальной величины независимого аргумента t и его конечного значения.

Далее задаются начальные условия. Значения всех неизвестных искомых переменных в начале расчёта задаются в виде столбца соответствующей размерности.

Далее, при необходимости, задаются опции. Вот тут и раскрываются широкие возможности MATLAB по настройке решателя. Помимо управления точностью и величиной шага, имеется возможность обрабатывать данные в процессе вычисления, а также выполнять скрипты по завершению вычисления. Но ещё более полезным является опция отслеживания событий по условию, более подробно поговорим об этом дальше. Также есть другие специальные опции, которые могут быть использованы при решении определённых типов систем.

Вы могли заметить, что название функции — odeXY – это обозначение для всех решателей, которых всего 8 штук. В данном ролике мы пользоваться решателем ode45, соответствующего численному по методу Дормана-Принса 4(5). Этого решателя достаточно для подавляющего большинства задач. Остальные решатели будут подробно рассмотрены в приложении к задачам соответствующих типов позже.

Перейдем к примерам.

Рассмотрим 2 примера:

• решение дифференциального уравнения первого порядка.
• решение системы двух дифференциальных уравнений второго порядка.

В качестве уравнение первого порядка рассмотрим логистическое уравнение Ферхюльста, которое описывает динамику численности популяции. Суть уравнения такова: скорость прироста населения y пропорциональна количеству населения, однако лимитирована максимальной численностью популяции.

Забавный факт: Ферхюльст назвал это уравнение логистическим, и никто до сих пор не знает почему, ибо сам Ферхюльст об этом никому не рассказал.

Решение этого дифференциального уравнения выглядит следующим образом.

Пишем функцию в явном виде, задаём интервал расчёта и записываем начальное условие. Пару слов о записи функции подобным образом. Знак собаки в матлабе является оператором создания функции соответствующих переменных. Вы задаёте аргументы функции и саму функцию через пробел, как показано на рисунке.

Перейдем в окно MATLABа и посмотрим, как это выглядит.

Так выглядит скрипт:

Так выглядит график решения дифференциального уравнения:

В качестве примера решения системы, состоящей из двух дифференциальных уравнений второго порядка, рассмотрим шарик, подвешенный на пружине, который ещё и тормозит о воздух.

Уравнения показаны на рисунке. Но вид системы отличается от требуемого, в том числе потому, что в нём присутствуют вторые производные. Для приведения системы в требуемый вид выполним 2 простых шага:

Первое: следует заменить переменные соответствующим образом. Теперь у нас 4 неизвестных. Далее следует преобразовать уравнение с учетом замены. Таким образом, мы имеем систему из четырёх дифференциальных уравнений первого порядка.

Настало время её записать.

Итак, мы имеем систему, параметры, интервал времени и начальные условия. Решим же эту задачу скорее.

В отличие от предыдущего примера, систему четырех уравнений проблематично записать в поле аргумента. Поэтому всю систему будем записывать в отдельную функцию.

Эту функцию можно располагать как в самом скрипте решения в самом его конце, так и в виде отдельного m-файла.

На выходе функция должна представлять собой вектор-столбец, который записывается перечислением компонент через точку запятой как показано на рисунке.

Теперь рассмотрим скрипт самого решения.

На этот раз запишем интервал и начальные условия в виде переменных MATLAB. Интервал, соответственно, в виде строки, а начальные условия – в виде столбца длинной 4.

Сообразно с уже разобранным ранее синтаксисом укажем функцию pendulum_np, интервал времени и начальные условия.

Перейдем теперь в окно MATLAB и посмотрим решение.

Так выглядит скрипт:

Запускаем скрипт и получаем графики:

Зачастую хочется, чтобы одну и ту же систему можно было бы решать с разными параметрами, и при этом не менять их в теле самой функции. И это можно, и даже нужно осуществлять.

На рисунке показана функция MATLAB, которая соответствует движению подвешенного на пружине шара, однако можно заметить, что эта функция теперь имеет на 5 аргументов больше.

Параметры задаются в скрипте, а при вызове функции мы обращаемся к уже известному оператору-собаке, которая превращает функцию семи переменных pendulum_n в функцию двух переменных t и X. Вот и всё.

Я вам очень рекомендую разобраться с тем, как работает оператор-собака. В хелпе он называется function-handle. Разобравшись с ним Вам будет работать в среде MATLAB ещё проще и ещё приятнее.

Вывод: не так страшно решать диффуры

Под конец стоит сказать какие вообще системы дифференциальных уравнений матлаб может решать, а может он решать системы практически любых типов.

Их можно, с одной стороны, разделить по степени жёсткости, а с другой стороны, по структуре самой системы.

Когда уравнения представляют поведение системы, которая содержит ряд быстрых и медленных реакций, то такую систему уравнения можно назвать жесткой. Для жестких задач явные численные методы работают плохо, или не работают вовсе. Примером жесткой задачи может являться протекание тока через клеточную мембрану. На самом деле, чёткого разделения между жесткими и нежёсткими системами не существует. Степень жесткости системы формально определяется через собственные значения матрицы Якоби, но давайте не будем закапываться.

Видеообзор по теме решения систем Д/У доступен по ссылке.