Матричная форма системы нормальных уравнений

Матричная форма системы нормальных уравнений

В матричной форме система нормальных уравнений запишется следующим образом [c.248]

Такая система имеет обычно единственное решение. В исключительных случаях, когда столбцы системы линейных уравнений линейно зависимы, она имеет бесконечно много решений или не имеет решения вовсе. Однако данные реальных статистических наблюдений к таким исключительным случаям практически никогда не приводят. Система (6.11) называется системой нормальных уравнений. Ее решение в явном виде наиболее наглядно представимо в векторно-матричной форме. [c.145]

Минимизируемая функция G является квадратичной относительно неизвестных величин at. Необходимым условием ее минимума является равенство нулю всех ее частных производных по аг Частные производные квадратичной функции являются линейными функциями, и, приравнивая их всех к нулю, мы получим систему из (т+1) линейных уравнений с (/я+1) неизвестными. Такая система имеет обычно единственное решение (за исключением особого еду чая, кргда столбцы ее линейно зависимы и решения,»нет или их бесконечно много однако данные реальных статистических наблюдений к такому особому случаю, вообще говоря, никогда не приводят). Данная система называется системой нормальных уравнений. Ее решение в явном виде удобнее всего выписать в векторно-мат-ричной форме, иначе оно становится слишком громоздким. Вектор-но-матричная запись и вывод решения системы нормальных уравнений приведены в Приложении при начальном ознакомлении с проблемой оно может быть опущено. [c.309]

Матричная форма системы уравнений

СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

Это один из основных разделов в алгебре. Нет такой отрасли науки и приложений, где в том или ином виде не использовались бы системы линейных алгебраических уравнений. При решении экономических задач системы линейных уравнений наиболее употребимы как в аппарате исследования, так и при рассмотрении частных проблем.

Основные понятия

Общий вид и свойства системы уравнений

Система т линейных уравнений с п неизвестными (переменными) х₁, х₂, …, x_nимеет вид

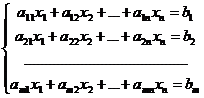(16.1)

Здесь a_ijи b_j— произвольные числа (i = 1, 2, . m; j= 1, 2, . n), которые называются соответственно коэффициентами при неизвестных и свободными членами уравнений (16.1). Первый индекс у коэффициентов при неизвестных означает номер уравнения, второй индекс соответствует номеру неизвестного x_i/

Решением системы уравнений (16.1) называется набор п чисел , , …, ,приподстановке которых в эту систему каждое уравнение данной системы превращается в тождество.

Система уравнений (16.1) называется совместной, если она имеет хотя бы одно решение; если система не имеет решений, она называется несовместной. Совместная система уравнений имеет либо одно решение, и в таком случае она называется определенной, либо, если у нее больше одного решения, она называется неопределенной.

Системы уравнений вида (16.1) называются эквивалентными, если они имеют одно и то же множество решений. Элементарные преобразования исходной системы приводят к эквивалентной системе. К элементарным преобразованиям относятся:

1) вычеркивание уравнения 0х₁+ 0x₂ + … + 0x_n = 0 — нулевой строки;

2) перестановка уравнений или слагаемых a_ijx_j в уравнениях;

3) прибавление к обеим частям одного уравнения соответственно обеих частей другого уравнения этой системы, умноженного на любое действительное число;

4) удаление уравнений, являющихся линейными комбинациями других уравнений системы.

Последнее свойство вытекает из третьего свойства: если какое-либо уравнение представляет собой линейную комбинацию других уравнений, то из него можно сформировать нулевую строку.

Матричная форма системы уравнений

Сведем коэффициенты при неизвестных в системе уравнений (16.1) в матрицу

(16.2)

Эта матрица состоит из т строк и п столбцов и называется матрицей системы. Введем в рассмотрение две матрицы-столбца: матрицу неизвестных X и матрицу свободных членов В:

(16.3)

X и В представляют собой векторы-столбцы, однако в целях единого подхода в рамках матричной алгебры удобнее трактовать их именно как матрицы, состоящие соответственно из п и т строк и одного столбца.

Тогда систему линейных уравнений (16.1) можно записать в матричной форме, поскольку размер матрицы А равен т х п а размер X — п х 1, значит, произведение этих матриц имеет смысл:

Произведение матриц АХ является, как и В, матрицей-столбцом размера mxl, состоящей из левых частей уравнений системы (16.1). Все уравнения этой системы вытекают из уравнения (16.4) в силу определения 2 равенства двух матриц.

Введем в рассмотрение еще одну матрицу; дополним матрицу системы А столбцом свободных членов и получим новую матрицу размера т х (n + 1):

(16.5)

Матрица А_В называется расширенной матрицей системы. Эта матрица играет важную роль в вопросе о разрешимости системы уравнений.

Теорема 16.1(теорема Кронекера-Капелли; критерий совместности системы). Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы.

Доказательство этой теоремы мы не приводим.

Системы линейных алгебраических уравнений: основные понятия, виды

Определение СЛАУ

Системой линейных алгебраических уравнений (СЛАУ) называется система вида:

$$\left\<\begin a_ <11>\cdot x_<1>+a_ <12>\cdot x_<2>+\ldots+a_ <1 n>\cdot x_=b_ <1>\\ a_ <21>\cdot x_<1>+a_ <22>\cdot x_<2>+\ldots+a_ <2 n>\cdot x_=b_ <2>\\ \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots . . \\ a_ \cdot x_<1>+a_ \cdot x_<2>+\ldots+a_ \cdot x_=b_ \end\right.$$

Упорядоченный набор значений $$\left\^<0>, x_<2>^<0>, \ldots, x_^<0>\right\>$$ называется решением системы, если при подстановке в уравнения все уравнения превращаются в тождество.

Задание. Проверить, является ли набор $<0,3>$ решением системы $\left\<\begin 3 x-2 y=-6 \\ 5 x+y=3 \end\right.$

Решение. Подставляем в каждое из уравнений системы $x=0$ и $y=3$:

$$5 x+y=3 \Rightarrow 5 \cdot 0+3=3 \Rightarrow 3=3$$

Так как в результате подстановки получили верные равенства, то делаем вывод, что заданный набор является решением указанной СЛАУ.

Ответ. Набор $<0,3>$ является решением системы $\left\<\begin 3 x-2 y=-6 \\ 5 x+y=3 \end\right.$

Виды систем

СЛАУ называется совместной, если она имеет, хотя бы одно решение.

В противном случае система называется несовместной.

Система $\left\<\begin 3 x-2 y=-6 \\ 5 x+y=3 \end\right.$ является совместной, так как она имеет, по крайней мере, одно решение $x=0$, $y=3$

Система $\left\<\begin 5 x+y=-6 \\ 5 x+y=3 \end\right.$ является несовместной, так как выражения, стоящие в левых частях уравнений системы равны, но правые части не равны друг другу. Ни для каких наборов $$ это не выполняется.

Система называется определённой, если она совместна и имеет единственное решение.

В противном случае (т.е. если система совместна и имеет более одного решения) система называется неопределённой.

Система называется однородной, если все правые части уравнений, входящих в нее, равны нулю одновременно.

Система называется квадратной, если количество уравнений равно количеству неизвестных.

Система $\left\<\begin 3 x-2 y=-6 \\ 5 x+y=3 \end\right.$ квадратная, так как неизвестных две и это число равно количеству уравнений системы.

Матричная запись систем уравнений

Исходную СЛАУ можно записать в матричном виде:

Задание. Систему $\left\<\begin x-y+z-4 t=0 \\ 5 x+y+t=-11 \end\right.$ записать в матричной форме и выписать все матрицы, которые ей соответствуют.

Решение. Заданную СЛАУ записываем в матричной форме $A. X=B$ , где матрица системы:

$$A=\left(\begin 1 & -1 & 1 & -4 \\ 5 & 1 & 0 & 1 \end\right)$$

то есть, запись СЛАУ в матричной форме:

$$\left(\begin 1 & -1 & 1 & -4 \\ 5 & 1 & 0 & 1 \end\right)\left(\begin x \\ y \\ z \\ t \end\right)=\left(\begin 0 \\ -11 \end\right)$$

Расширенная матрица системы

Задание. Записать матрицу и расширенную матрицу системы $\left\<\begin 2 x_<1>+x_<2>-x_<3>=4 \\ x_<1>-x_<2>=5 \end\right.$

Решение. Матрица системы $A=\left(\begin 2 & 1 & -1 \\ 1 & -1 & 0 \end\right)$ , тогда расширенная матрица $\tilde=(A \mid B)=\left(\begin 2 & 1 & -1 & 4 \\ 1 & -1 & 0 & 5 \end\right)$