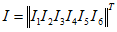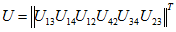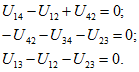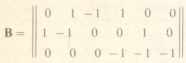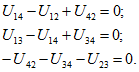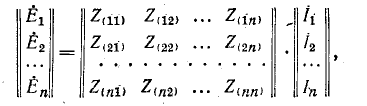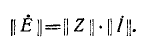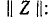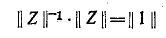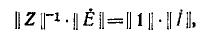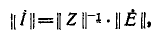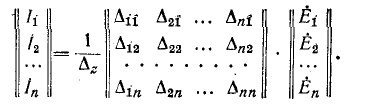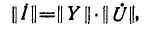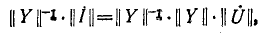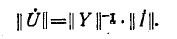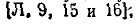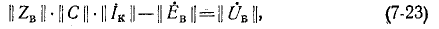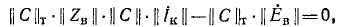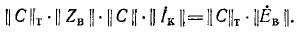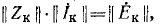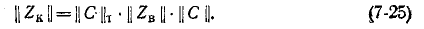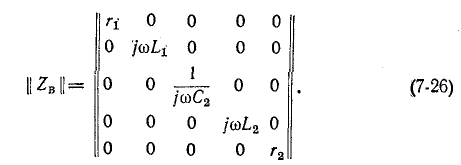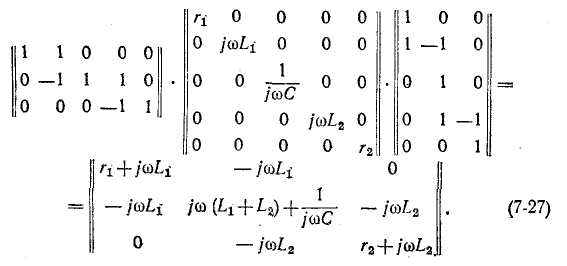Трансформаторные подстанции высочайшего качества
с нами приходит энергия
develop@websor.ru
Законы Кирхгофа в матричной форме
Для записи законов Кирхгофа в матричной форме необходимо составить топологические матрицы схемы.
Матрица соединений , или узловая А ,- это таблица коэффициентов независимых уравнений, составленных по первому закону Кирхгофа для У — 1 узлов. Строки (i) соответствуют узлам (их число равно У- 1), столбцы ( j ) — ветвям (их число равно В). Элемент матрицы aij = + 1, если ветвь j графа соединена с узлом i и направлена от узла i (положительное направление тока в ветви j выбрано от узла i). Элемент матрицы aij = — 1, если ветвь j графа соединена с узлом i и направлена к узлу i . Элемент матрицы aij = 0, если ветвь j не присоединена к узлу i .
Например, для схемы и графа по рис. 1.14 с У= 4 узлами и В = 6 ветвями для первых трех узлов
что соответствует первым трем уравнениям ( 1.21а).
Так как -матрица А определяет, какие ветви присоединены к каждому узлу и как направлены токи в этих ветвях, то произведение матрицы соединений на матрицу-столбец токов ветвей I дает совокупность левых частей уравнений, составленных по первому закону Кирхгофа, и, следовательно, равно нулю:
А I = 0 (1.26а)
— это первый закон Кирхгофа в матричной форме. Для схемы и графа по рис. 1.14
и после выполнения умножения матриц получаем первые три уравнения (1.21а).
Под матрицей соединений иногда понимают матрицу А , записанную для всех узлов схемы.
Матрица сечений Q — это таблица коэффициентов, составленных по первому закону Кирхгофа для сечений. Строки i матрицы соответствуют сечениям (их число равно У — 1), столбцы j — ветвям (их число равно В). Элемент матрицы q ij = +1, если ветвь j содержится в сечении i и направлена согласно с направлением сечения. Элемент матрицы q ij = -1, если ветвь j содержится в сечении i и направлена противоположно направлению сечения. Элемент матрицы q ij = 0, если ветвь j не содержится в сечении i . Для главных сечений составляется матрица главных сечений .
Например, для графа рис. 1.14, д при показанных трех главных сечениях
В матричной форме первый закон Кирхгофа можно записать и с матрицей сечений
После умножения матрицы Q на матрицу-столбец токов I получаются первое и третье (с обратным знаком) уравнения (1.21а) и уравнение (1.216), т. е. независимая система уравнений по первому закону Кирхгофа.
Матрица контуров В — это таблица коэффициентов независимых уравнений, составленных по второму закону Кирхгофа для К = В — (У- 1) независимых контуров. Строки к соответствуют контурам (их число равно К), столбцы j — ветвям (их число равно В).
Элемент матрицы b kj =+1, если ветвь j входит в состав контура k и ее направление совпадает с направлением обхода контура. Элемент матрицы b kj ,= -1, если ветвь j входит в состав контура k и ее направление противоположно направлению обхода контура. Элемент матрицы b kj = 0, если ветвь j не входит в состав контура k .
Матрица В, составленная для главных контуров, приводит непосредственно к независимой системе уравнений по второму закону Кирхгофа. Например, для графа рис. 1.14, д с контурами, состоящими из ветвей 2-4-3 (а), 5-6-4 (б) и 1-6-3 (в) матрица главных контуров при их обходе по направлению движения часовой стрелки
Умножив матрицу В на матрицу-столбец напряжений ветвей, получим матричное уравнение по второму закону Кирхгофа в формулировке (1.20а)
так как каждая строка матрицы В определяет, какие ветви входят в соответствующий контур и с какими знаками должны быть записаны напряжения ветвей.
Для схемы по рис. 1.14, а и ее графа по рис. 1.14, в после умножения на матрицу-столбец напряжений ветвей
получим систему трех независимых уравнений вида (1.20а):
Эта система с учетом равенства 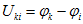
Для любой планарной схемы , т. е. схемы, которую можно изобразить на листе без пересекающихся ветвей и проводов, в качестве независимых контуров можно выбирать элементарные контуры-ячейки. Например, для схемы рис. 1.14, а это ячейки I , II , III. Если выбрать направление обхода каждой ячейки по направлению движения стрелки часов, то
После умножения на матрицу-столбец напряжений ветвей U получим другую независимую систему уравнений по второму закону Кирхгофа в форме (1.20 а):
которая после подстановки соотношений (1.22а) приводится к виду (1.206).
Если схема цепи кроме источников ЭДС, как на рис. 1.14, а (и далее рис. 1.20-1.22), содержит и источники тока, то для записи матричных уравнений (1.27) можно рекомендовать преобразование источников тока в источники ЭДС (см. рис. 1.23) или введение понятия обобщенной ветви (см. рис. 1.25).
Матричная форма записи уравнений по законам кирхгофа
Рассмотренные методы расчета электрических цепей – непосредственно по законам Кирхгофа, методы контурных токов и узловых потенциалов – позволяют принципиально рассчитать любую схему. Однако их применение без использования введенных ранее топологических матриц рационально для относительно простых схем. Использование матричных методов расчета позволяет формализовать процесс составления уравнений электромагнитного баланса цепи, а также упорядочить ввод данных в ЭВМ, что особенно существенно при расчете сложных разветвленных схем.
Переходя к матричным методам расчета цепей, запишем закон Ома в матричной форме.
Пусть имеем схему по рис. 1, где 
 . . | (1) |
Однако, для дальнейших выкладок будет удобнее представить ток 
 . . | (2) |
Подставив (2) в (1), получим:
 . . | (3) |
Формула (3) представляет собой аналитическое выражение закона Ома для участка цепи с источниками ЭДС и тока (обобщенной ветви).
Соотношение (3) запишем для всех n ветвей схемы в виде матричного равенства
 , , | (4) |
где Z – диагональная квадратная (размерностью матрица сопротивлений ветвей, все элементы которой (взаимную индуктивность не учитываем), за исключением элементов главной диагонали, равны нулю.
Соотношение (4) представляет собой матричную запись закона Ома.
Если обе части равенства (4) умножить слева на контурную матрицу В и учесть второй закон Кирхгофа, согласно которому
 , , | (5) |
 , , | (6) |
то есть получили новую запись в матричной форме второго закона Кирхгофа.
Метод контурных токов в матричной форме
В соответствии с введенным ранее понятием матрицы главных контуров В , записываемой для главных контуров, в качестве независимых переменных примем токи ветвей связи, которые и будут равны искомым контурным токам.
Уравнения с контурными токами получаются на основании второго закона Кирхгофа; их число равно числу независимых уравнений, составляемых для контуров, т.е. числу ветвей связи c = n — m +1 . Выражение (6) запишем следующим образом:
 . . | (7) |
В соответствии с методов контурных токов токи всех ветвей могут быть выражены как линейные комбинации контурных токов или в рассматриваемом случае токов ветвей связи. Если элементы j –го столбца матрицы В умножить соответствующим образом на контурные токи, то сумма таких произведений и будет выражением тока j –й ветви через контурные токи (через токи ветвей связи). Сказанное может быть записано в виде матричного соотношения
 , , | (8) |
где 

С учетом (8) соотношение (7) можно записать, как:
 | (9) |
Полученное уравнение представляет собой контурные уравнения в матричной форме. Если обозначить
 , , | (10) |
 . . | (11) |
то получим матричную форму записи уравнений, составленных по методу контурных токов:
 , , | (12) |
где 

В развернутой форме (12) можно записать, как:
 , , | (13) |
то есть получили известный из метода контурных токов результат.
Рассмотрим пример составления контурных уравнений.
Пусть имеем схему по рис. 2. Данная схема имеет четыре узла ( m =4) и шесть обобщенных ветвей ( n =6). Число независимых контуров, равное числу ветвей связи,
Граф схемы с выбранным деревом (ветви 1, 2, 3) имеет вид по рис. 3.
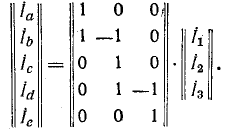
Запишем матрицу контуров, которая будет являться матрицей главных контуров, поскольку каждая ветвь связи входит только в один контур. Принимая за направление обхода контуров направления ветвей связи, получим:
B
Диагональная матрица сопротивлений ветвей
Z
Матрица контурных сопротивлений
Zk=BZB T

Матрицы ЭДС и токов источников
 |  |
 |  |
Тогда матрица контурных ЭДС

Матрица контурных токов
 |  . . |
Таким образом, окончательно получаем:

где 








Анализ результатов показывает, что полученные три уравнения идентичны тем, которые можно записать непосредственно из рассмотрения схемы по известным правилам составления уравнений по методу контурных токов.
Метод узловых потенциалов в матричной форме
На основании полученного выше соотношения (4), представляющего собой, как было указано, матричную запись закона Ома, запишем матричное выражение:
 , , | (14) |
где 

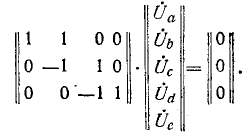
Умножив обе части равенства (14) на узловую матрицу А и учитывая первый закон Кирхгофа, согласно которому
 , , | (15) |
 .. .. | (16) |
Выражение (16) перепишем, как:
 . . | (17) |
Принимая потенциал узла, для которого отсутствует строка в матрице А , равным нулю, определим напряжения на зажимах ветвей:
 . . | (18) |
Тогда получаем матричное уравнение вида:
 . . | (19) |
Данное уравнение представляет собой узловые уравнения в матричной форме. Если обозначить
 | (20) |
 , , | (21) |
то получим матричную форму записи уравнений, составленных по методу узловых потенциалов:
 | (22) |
где 

В развернутом виде соотношение (22) можно записать, как:
 | (23) |
то есть получили известный из метода узловых потенциалов результат.
Рассмотрим составление узловых уравнений на примере схемы по рис. 4.
Данная схема имеет 3 узла ( m =3) и 5 ветвей ( n =5) . Граф схемы с выбранной ориентацией ветвей представлен на рис. 5.
А
Диагональная матрица проводимостей ветвей:
Y
где 
Матрица узловых проводимостей

Матрицы токов и ЭДС источников
 |  |
 |  |
Следовательно, матрица узловых токов будет иметь вид:
Таким образом, окончательно получаем:

где 




Анализ результатов показывает, что полученные уравнения идентичны тем, которые можно записать непосредственно из рассмотрения схемы по известным правилам составления уравнений по методу узловых потенциалов.
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
- В чем заключаются преимущества использования матричных методов расчета цепей?
- Запишите выражения матрицы контурных сопротивлений и матрицы контурных ЭДС.
- Запишите выражения матрицы узловых проводимостей и матрицы узловых токов.
- Составить узловые уравнения для цепи на рис. 2.
Составить контурные уравнения для цепи рис. 4, приняв, что дерево образовано ветвями 3 и 4 (см. рис. 5).
Применение матриц к расчету электрических цепей
Применение матриц к расчету электрических цепей:
Математическая символика и правила матричной алгебры позволяют упростить запись систем уравнений, получающихся при расчете сложных электрических цепей. В этом отношении матричную алгебру можно сравнить со стенографией, которая облегчает и ускоряет запись.
Напомним, что матрица представляет собой совокупность величин, называемых ее элементами и расположенных в виде прямоугольной таблицы 1. Если число строк равно числу столбцов, то матрица называется квадратной. Матрица, содержащая один столбец, называется столбцовой или матрицей-столбцом.
Приведенная система уравнений, записанных по второму закону Кирхгофа для контурных э. д. с. и контурных токов, может быть представлена в виде произведений квадратной матрицы собственных и общих сопротивлений контуров на столбцовую матрицу контурных токов.
При этом следует помнить, что произведением двух матриц называется матрица, элементы которой равны сумме произведений всех элементов соответствующей строки первой матрицы на соответствующие элементы столбца второй матрицы. Итак, уравнения (7-2) в матричной форме имеют вид:
Данное матричное уравнение может быть решено относительно матрицы 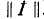
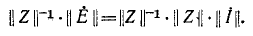
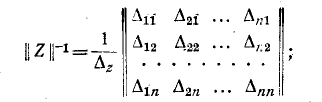
Как известно, для получения обратной матрицы необходимо заменить в исходной матрице-каждый элемент его алгебраическим дополнением, затем заменить строки соответствующими столбцами 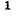
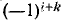
здесь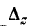
Произведение обратной матрицы на исходную матрицу равно единичной матрице, т. е. квадратной матрице, у которой все элементы главной диагонали (идущей от левого верхнего угла к правому нижнему) равны единице, а остальные элементы равны нулю.
где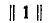
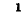
Произведение единичной матрицы на матрицу 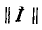
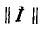
или в развернутой форме
В результате умножения матриц получаются выражения для контурных токов вида (7-4).
Аналогично решается матричное уравнение для узловых напряжений
где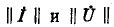
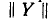
В результате умножения матрицы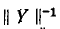
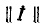
Матричная алгебра широко применяется для расчета сложных четырехполюсников.
В случае относительно простой электрической схемы без взаимной индукции матрица контурных сопротивлений легко записывается непосредственно по заданной схеме. В более сложных случаях матрица контурных сопротивлений может быть получена с помощью матрицы сопротивлений ветвей. Ниже показана связь, существующая между матрицами контурных сопротивлений и сопротивлений ветвей 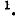
•Обозначим токи, напряжения, э. д. с. и сопротивления ветвей индексом «в», а соответствующие контурные величины — индексом «к». Связь между токами в ветвях и контурными токами выражается зависимостью
Здесь 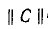
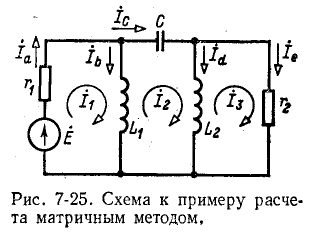
Например, для схемы рис. 7-25 имеем:
Уравнения вида (М2) по второму закону Кирхгофа в матричной форме записываются так:
где 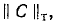
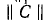
Строка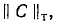
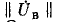
любом контуре равна нулю, т. е. «произведение» любой строки 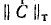
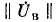
Например, для схемы рис, 7-25 имеем:
Считая, что направления э. д. с. и токов в ветвях совпадают, получаем матрицу напряжений на ветвях в виде
Подстановка (7-20) и (7-22) дает:
а подстановкой (7-23) в (7-21) получаем:
Сопоставив это уравнение с уравнением для контурных токов
приходим к выводу, что э. д. с. в ветвях и контурные э. д. с. связаны матричным уравнением
а матрица контурных сопротивлений получается по формуле
Для схемы рис. 7-25 матрица сопротивлений ветвей записывается в виде
Матрица контурных сопротивлений согласно (7-25) равна:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Дуальные цепи
- Электромеханические аналогии
- Индуктивно связанные электрические цепи
- Фильтры и топологические методы анализа линейных электрических цепей
- Теорема обратимости (или взаимности)
- Теорема компенсации
- Теорема об изменении токов в электрической цепи при изменении сопротивления в одной ветви
- Теорема об эквивалентном источнике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://toehelp.ru/theory/toe/lecture06/lecture06.html
http://www.evkova.org/primenenie-matrits-k-raschetu-elektricheskih-tsepej