Матричный метод онлайн
Данный онлайн калькулятор решает систему линейных уравнений матричным методом. Дается очень подробное решение. Для решения системы линейных уравнений выберите количество переменных. Выбирайте метод вычисления обратной матрицы. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Матричный метод решения систем линейных уравнений
Рассмотрим следующую систему линейных уравнений:
 | (1) |
Для решения системы линейных уравнений (1) матричным методом запишем ее матричном виде:
| Ax=b, | (2) |
  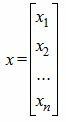 | (3) |
Мы будем предполагать, что матрица A имеет обратное, т.е. определитель матрицы A не равен нулю.
Умножим матричное уравнение (2) на обратную матрицу A −1 . Тогда
| A −1 Ax=A −1 b. | (4) |
Учитывая определение обратной матрицы, имеем A −1 A=E, где E— единичная матрица. Следовательно (4) можно записать так:
| Ex=A −1 b. | (4) |
или, учитывая, что Ex=x:
| x=A −1 b. | (5) |
Таким образом, для решения системы линейных уравнений (1) (или (2)), достаточно умножить обратную к A матрицу на вектор ограничений b.
Примеры решения системы линейных уравнений матричным методом
Пример 1. Решить следующую систему линейных уравнений матричным методом:
 |
Матричный вид записи системы линейных уравнений: Ax=b, где
 . . |
Найдем обратную к матрице A методом Жордана-Гаусса. С правой стороны матрицы A запишем единичную матрицу:
 . . |
Выбираем самый большой по модулю ведущий элемент столбца 1. Для этого заменяем местами строки 1 и 2:
 . . |
Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/3,-1/3 соответственно:
 . . |
Выбираем самый большой по модулю ведущий элемент столбца 2. Для этого заменяем местами строки 2 и 3:
 . . |
Исключим элементы 2-го столбца матрицы ниже главной диагонали. Для этого сложим строку 3 со строкой 2, умноженной на -24/51:
 . . |
Исключим элементы 3-го столбца матрицы выше главной диагонали. Для этого сложим строки 1, 2 со строкой 3, умноженной на 17/53, 85/159 соответственно:
 . . |
Исключим элементы 2-го столбца матрицы выше главной диагонали. Для этого сложим строку 1 со строкой 2, умноженной на -3/17:
 . . |
Делим каждую строку матрицы на ведущий элемент соответствующей строки:
 . . |
Отделяем правую часть матрицы. Полученная матрица является обратной матрицей к A :
 . . |
Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A−1b. Тогда
  . . |
 |
Пример 2. Решить следующую систему линейных уравнений матричным методом:
 . . |
Матричный вид записи системы линейных уравнений: Ax=b, где
 . . |
Найдем обратную к матрице A методом алгебраических дополнений. Вычислим определитель матрицы A :
 . . |
Вычислим все алгебраические дополнения матрицы A:
 , , |
 , , |
 , , |
 , , |
 , , |
 , , |
 , , |
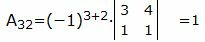 , , |
 . . |
Обратная матрица вычисляется из следующего выражения:
 |
где Aij − алгебраическое дополнение элемента матрицы A, находящиеся на пересечении i-ой строки и j-ого столбца, а Δ − определитель матрицы A.
Используя формулу обратной матрицы, получим:
 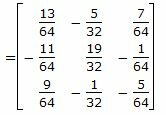 |
Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A −1 b. Тогда
Линейные уравнения. Решение систем линейных уравнений матричным методом.
Матричный метод решения СЛАУ применяют к решению систем уравнений, у которых количество уравнений соответствует количеству неизвестных. Метод лучше применять для решения систем низкого порядка. Матричный метод решения систем линейных уравнений основывается на применении свойств умножения матриц.
Этот способ, другими словами метод обратной матрицы, называют так, так как решение сводится к обычному матричному уравнению, для решения которого нужно найти обратную матрицу.
Матричный метод решения СЛАУ с определителем, который больше или меньше нуля состоит в следующем:
Предположим, есть СЛУ (система линейных уравнений) с n неизвестными (над произвольным полем):
Значит, её легко перевести в матричную форму:
AX=B, где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:
Умножим это матричное уравнение слева на A −1 — обратную матрицу к матрице A: A −1 (AX)=A −1 B.
Т.к. A −1 A=E, значит, X=A −1 B. Правая часть уравнения дает столбец решений начальной системы. Условием применимости матричного метода есть невырожденность матрицы A. Необходимым и достаточным условием этого есть неравенство нулю определителя матрицы A:
Для однородной системы линейных уравнений, т.е. если вектор B=0, выполняется обратное правило: у системы AX=0 есть нетривиальное (т.е. не равное нулю) решение лишь когда detA=0. Эта связь между решениями однородных и неоднородных систем линейных уравнений называется альтернатива Фредгольма.
Т.о., решение СЛАУ матричным методом производится по формуле 
Известно, что у квадратной матрицы А порядка n на n есть обратная матрица A −1 только в том случае, если ее определитель ненулевой. Таким образом, систему n линейных алгебраических уравнений с n неизвестными решаем матричным методом только в случае, если определитель основной матрицы системы не равен нулю.
Не взирая на то, что есть ограничения возможности применения такого метода и существуют сложности вычислений при больших значениях коэффициентов и систем высокого порядка, метод можно легко реализовать на ЭВМ.
Пример решения неоднородной СЛАУ.
Для начала проверим, не равен ли нулю определитель матрицы коэффициентов у неизвестных СЛАУ.
Далее вычисляем алгебраические дополнения для элементов матрицы, которая состоит из коэффициентов при неизвестных. Эти коэффициенты нужны будут для вычисления обратной матрицы.
Теперь находим союзную матрицу, транспонируем её и подставляем в формулу для определения обратной матрицы.
Подставляем переменные в формулу:
Теперь находим неизвестные, перемножая обратную матрицу и столбик свободных членов.
При переходе от обычного вида СЛАУ к матричной форме будьте внимательными с порядком неизвестных переменных в уравнениях системы. Например:
НЕЛЬЗЯ записать как:
Необходимо, для начала, упорядочить неизвестные переменные в кадом уравнении системы и только после этого переходить к матричной записи:
Кроме того, нужно быть внимательными с обозначением неизвестных переменных, вместо x1, x2, …, xn могут оказаться другие буквы. К примеру:
в матричной форме записываем так:
Матричным методом лучше решать системы линейных уравнений, в которых количество уравнений совпадает с числом неизвестных переменных и определитель основной матрицы системы не равен нулю. Когда в системе более 3-х уравнений, на нахождение обратной матрицы потребуется больше вычислительных усилий, поэтому, в этом случае целесообразно использовать для решения метод Гаусса.
Решение систем линейных уравнений матричным методом
Вы будете перенаправлены на Автор24
Матричный способ решения систем линейных уравнений
Рассмотрим систему линейных уравнений следующего вида:
Числа $a_
В случае, когда все свободные члены равны нулю, система называется однородной, в противном случае — неоднородной.
Каждой СЛАУ можно поставить в соответствие несколько матриц и записать систему в так называемом матричном виде.
Матрица коэффициентов системы называется матрицей системы и обозначается, как правило, буквой $A$.
Столбец свободных членов образует вектор-столбец, который, как правило, обозначается буквой $B$ и называется матрицей свободных членов.
Неизвестные переменные образуют вектор-столбец, который, как правило, обозначается буквой $X$ и называется матрицей неизвестных.
Описанные выше матрицы имеют вид:
Используя матрицы, СЛАУ можно переписать в виде $A\cdot X=B$. Такую запись часто называют матричным уравнением.
Вообще говоря, в матричном виде записать можно любую СЛАУ.
Примеры решения системы с помощью обратной матрицы
Дана СЛАУ: $\left\<\begin
Решение:
В случае, когда матрица системы является квадратной, СЛАУ можно решить уравнения матричным способом.
Имея матричное уравнение $A\cdot X=B$, можно выразить из него $X$ следующим способом:
$A^ <-1>\cdot A\cdot X=A^ <-1>\cdot B$
$A^ <-1>\cdot A=E$ (свойство произведения матриц)
$E\cdot X=A^ <-1>\cdot B$
$E\cdot X=X$ (свойство произведения матриц)
Алгоритм решения системы алгебраических уравнений с помощью обратной матрицы:
- записать систему в матричном виде;
- вычислить определитель матрицы системы;
- если определитель матрицы системы отличен от нуля, то находим обратную матрицу;
- решение системы вычисляем по формуле $X=A^ <-1>\cdot B$.
Готовые работы на аналогичную тему
Если матрица системы имеет определитель, не равный нулю, то данная система имеет единственное решение, которое можно найти матричным способом.
Если матрица системы имеет определитель, равный нулю, то данную систему нельзя решить матричным способом.
Дана СЛАУ: $\left\<\begin
Решение:
Нахождение определителя матрицы системы:
$\begin
Решим систему уравнений с помощью обратной матрицы:
Искомая обратная матрица:
Найдем решение системы:
$X=\left(\begin
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 18 11 2021
http://www.calc.ru/Lineynyye-Uravneniya-Resheniye-Sistem-Lineynykh-Uravneniy-Ma.html
http://spravochnick.ru/matematika/matricy/reshenie_sistem_lineynyh_uravneniy_matrichnym_metodom/















