Матричная запись и матричное решение системы уравнений

Матричный метод онлайн

Данный онлайн калькулятор решает систему линейных уравнений матричным методом. Дается очень подробное решение. Для решения системы линейных уравнений выберите количество переменных. Выбирайте метод вычисления обратной матрицы. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Матричный метод решения систем линейных уравнений

Рассмотрим следующую систему линейных уравнений:

(1)

Для решения системы линейных уравнений (1) матричным методом запишем ее матричном виде:

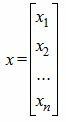(3)

Мы будем предполагать, что матрица A имеет обратное, т.е. определитель матрицы A не равен нулю.

Умножим матричное уравнение (2) на обратную матрицу A −1 . Тогда

Учитывая определение обратной матрицы, имеем A −1 A=E, где E— единичная матрица. Следовательно (4) можно записать так:

или, учитывая, что Ex=x:

Таким образом, для решения системы линейных уравнений (1) (или (2)), достаточно умножить обратную к A матрицу на вектор ограничений b.

Примеры решения системы линейных уравнений матричным методом

Пример 1. Решить следующую систему линейных уравнений матричным методом:

Матричный вид записи системы линейных уравнений: Ax=b, где

.

Найдем обратную к матрице A методом Жордана-Гаусса. С правой стороны матрицы A запишем единичную матрицу:

.

Выбираем самый большой по модулю ведущий элемент столбца 1. Для этого заменяем местами строки 1 и 2:

.

Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/3,-1/3 соответственно:

.

Выбираем самый большой по модулю ведущий элемент столбца 2. Для этого заменяем местами строки 2 и 3:

.

Исключим элементы 2-го столбца матрицы ниже главной диагонали. Для этого сложим строку 3 со строкой 2, умноженной на -24/51:

.

Исключим элементы 3-го столбца матрицы выше главной диагонали. Для этого сложим строки 1, 2 со строкой 3, умноженной на 17/53, 85/159 соответственно:

.

Исключим элементы 2-го столбца матрицы выше главной диагонали. Для этого сложим строку 1 со строкой 2, умноженной на -3/17:

.

Делим каждую строку матрицы на ведущий элемент соответствующей строки:

.

Отделяем правую часть матрицы. Полученная матрица является обратной матрицей к A :

.

Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A−1b. Тогда

.

Пример 2. Решить следующую систему линейных уравнений матричным методом:

.

Матричный вид записи системы линейных уравнений: Ax=b, где

.

Найдем обратную к матрице A методом алгебраических дополнений. Вычислим определитель матрицы A :

.

Вычислим все алгебраические дополнения матрицы A:

,

,

,

,

,

,

,

,

.

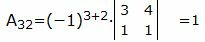Обратная матрица вычисляется из следующего выражения:

где A_ij − алгебраическое дополнение элемента матрицы A, находящиеся на пересечении i-ой строки и j-ого столбца, а Δ − определитель матрицы A.

Используя формулу обратной матрицы, получим:

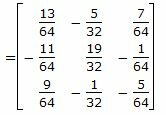Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A −1 b. Тогда

Система линейных алгебраических уравнений. Основные термины. Матричная форма записи.

Определение системы линейных алгебраических уравнений. Решение системы. Классификация систем.

Под системой линейных алгебраических уравнений (СЛАУ) подразумевают систему

содержащую $m$ уравнений и $n$ неизвестных ($x_1,x_2,\ldots,x_n$). Прилагательное «линейных» означает, что все неизвестные (их еще называют переменными) входят только в первой степени.

Параметры $a_$ ($i=\overline<1,m>$, $j=\overline<1,n>$) называют коэффициентами, а $b_i$ ($i=\overline<1,m>$) – свободными членами СЛАУ. Иногда, чтобы подчеркнуть количество уравнений и неизвестных, говорят так «$m\times n$ система линейных уравнений», – тем самым указывая, что СЛАУ содержит $m$ уравнений и $n$ неизвестных.

Если все свободные члены $b_i=0$ ($i=\overline<1,m>$), то СЛАУ называют однородной. Если среди свободных членов есть хотя бы один, отличный от нуля, СЛАУ называют неоднородной.

Решением СЛАУ (1) называют всякую упорядоченную совокупность чисел ($\alpha_1, \alpha_2,\ldots,\alpha_n$), если элементы этой совокупности, подставленные в заданном порядке вместо неизвестных $x_1,x_2,\ldots,x_n$, обращают каждое уравнение СЛАУ в тождество.

Любая однородная СЛАУ имеет хотя бы одно решение: нулевое (в иной терминологии – тривиальное), т.е. $x_1=x_2=\ldots=x_n=0$.

Если СЛАУ (1) имеет хотя бы одно решение, ее называют совместной, если же решений нет – несовместной. Если совместная СЛАУ имеет ровно одно решение, её именуют определённой, если бесконечное множество решений – неопределённой.

Имеем систему линейных алгебраических уравнений, содержащую $3$ уравнения и $5$ неизвестных: $x_1$, $x_2$, $x_3$, $x_4$, $x_5$. Можно, сказать, что задана система $3\times 5$ линейных уравнений.

Коэффициентами системы (2) есть числа, стоящие перед неизвестными. Например, в первом уравнении эти числа таковы: 3, -4, 1, 7, -1. Свободные члены системы представлены числами 11, -65, 0. Так как среди свободных членов есть хотя бы один, не равный нулю, то СЛАУ (2) является неоднородной.

Упорядоченная совокупность $(4;-11;5;-7;1)$ является решением данной СЛАУ. В этом несложно убедиться, если подставить $x_1=4$, $x_2=-11$, $x_3=5$, $x_4=-7$, $x_5=1$ в уравнения заданной системы:

Естественно, возникает вопрос том, является ли проверенное решение единственным. Вопрос о количестве решений СЛАУ будет затронут в соответствующей теме.

Система (3) является СЛАУ, содержащей $5$ уравнений и $3$ неизвестных: $x_1$, $x_2$, $x_3$. Так как все свободные члены данной системы равны нулю, то СЛАУ (3) является однородной. Несложно проверить, что совокупность $(0;0;0)$ является решением данной СЛАУ. Подставляя $x_1=0$, $x_2=0$, $x_3=0$, например, в первое уравнение системы (3), получим верное равенство:

$$4x_1+2x_2-x_3=4\cdot 0+2\cdot 0-0=0.$$

Подстановка в иные уравнения делается аналогично.

Матричная форма записи систем линейных алгебраических уравнений.

С каждой СЛАУ можно связать несколько матриц; более того – саму СЛАУ можно записать в виде матричного уравнения. Для СЛАУ (1) рассмотрим такие матрицы:

Матрица $A$ называется матрицей системы. Элементы данной матрицы представляют собой коэффициенты заданной СЛАУ.

Матрица-столбец $B$ называется матрицей свободных членов, а матрица-столбец $X$ – матрицей неизвестных.

Используя введённые выше обозначения, СЛАУ (1) можно записать в форме матричного уравнения: $A\cdot X=B$.

Матрицы, связанные с системой, можно записать различными способами: всё зависит от порядка следования переменных и уравнений рассматриваемой СЛАУ. Но в любом случае порядок следования неизвестных в каждом уравнении заданной СЛАУ должен быть одинаков (см. пример №4).

Записать СЛАУ $ \left \ < \begin& 2x_1+3x_2-5x_3+x_4=-5;\\ & 4x_1-x_3=0;\\ & 14x_2+8x_3+x_4=-11. \end \right. $ в матричной форме и указать расширенную матрицу системы.

Имеем четыре неизвестных, которые в каждом уравнении следуют в таком порядке: $x_1$, $x_2$, $x_3$, $x_4$. Матрица неизвестных будет такой: $\left( \begin x_1 \\ x_2 \\ x_3 \\ x_4 \end \right)$.

Свободные члены данной системы выражены числами -5, 0, -11, посему матрица свободных членов имеет вид: $B=\left( \begin -5 \\ 0 \\ -11 \end \right)$.

Перейдем к составлению матрицы системы. В первую строку данной матрицы будут занесены коэффициенты первого уравнения: 2, 3, -5, 1.

Во вторую строку запишем коэффициенты второго уравнения: 4, 0, -1, 0. При этом следует учесть, что коэффициенты системы при переменных $x_2$ и $x_4$ во втором уравнении равны нулю (ибо эти переменные во втором уравнении отсутствуют).

В третью строку матрицы системы запишем коэффициенты третьего уравнения: 0, 14, 8, 1. Учитываем при этом равенство нулю коэффициента при переменной $x_1$ (эта переменная отсутствует в третьем уравнении). Матрица системы будет иметь вид:

$$ A=\left( \begin 2 & 3 & -5 & 1\\ 4 & 0 & -1 & 0 \\ 0 & 14 & 8 & 1 \end \right) $$

Чтобы была нагляднее взаимосвязь между матрицей системы и самой системой, я запишу рядом заданную СЛАУ и ее матрицу системы:

В матричной форме заданная СЛАУ будет иметь вид $A\cdot X=B$. В развернутой записи:

$$ \left( \begin 2 & 3 & -5 & 1\\ 4 & 0 & -1 & 0 \\ 0 & 14 & 8 & 1 \end \right) \cdot \left( \begin x_1 \\ x_2 \\ x_3 \\ x_4 \end \right) = \left( \begin -5 \\ 0 \\ -11 \end \right) $$

Запишем расширенную матрицу системы. Для этого к матрице системы $ A=\left( \begin 2 & 3 & -5 & 1\\ 4 & 0 & -1 & 0 \\ 0 & 14 & 8 & 1 \end \right) $ допишем столбец свободных членов (т.е. -5, 0, -11). Получим: $\widetilde=\left( \begin 2 & 3 & -5 & 1 & -5 \\ 4 & 0 & -1 & 0 & 0\\ 0 & 14 & 8 & 1 & -11 \end \right) $.

Записать СЛАУ $ \left \ <\begin& 3y+4a=17;\\ & 2a+4y+7c=10;\\ & 8c+5y-9a=25; \\ & 5a-c=-4. \end\right.$ в матричной форме и указать расширенную матрицу системы.

Как видите, порядок следования неизвестных в уравнениях данной СЛАУ различен. Например, во втором уравнении порядок таков: $a$, $y$, $c$, однако в третьем уравнении: $c$, $y$, $a$. Перед тем, как записывать СЛАУ в матричной форме, порядок следования переменных во всех уравнениях нужно сделать одинаковым.

Упорядочить переменные в уравнениях заданной СЛАУ можно разными способами (количество способов расставить три переменные составит $3!=6$). Я разберу два способа упорядочивания неизвестных.

Введём такой порядок: $c$, $y$, $a$. Перепишем систему, расставляя неизвестные в необходимом порядке: $\left \ <\begin& 3y+4a=17;\\ & 7c+4y+2a=10;\\ & 8c+5y-9a=25; \\ & -c+5a=-4. \end\right.$

Матрица системы имеет вид: $ A=\left( \begin 0 & 3 & 4 \\ 7 & 4 & 2\\ 8 & 5 & -9 \\ -1 & 0 & 5 \end \right) $. Матрица свободных членов: $B=\left( \begin 17 \\ 10 \\ 25 \\ -4 \end \right)$. При записи матрицы неизвестных помним о порядке следования неизвестных: $X=\left( \begin c \\ y \\ a \end \right)$. Итак, матричная форма записи заданной СЛАУ такова: $A\cdot X=B$. В развёрнутом виде:

$$ \left( \begin 0 & 3 & 4 \\ 7 & 4 & 2\\ 8 & 5 & -9 \\ -1 & 0 & 5 \end \right) \cdot \left( \begin c \\ y \\ a \end \right) = \left( \begin 17 \\ 10 \\ 25 \\ -4 \end \right) $$

Расширенная матрица системы такова: $\left( \begin 0 & 3 & 4 & 17 \\ 7 & 4 & 2 & 10\\ 8 & 5 & -9 & 25 \\ -1 & 0 & 5 & -4 \end \right) $.

Введём такой порядок: $a$, $c$, $y$. Перепишем систему, расставляя неизвестные в необходимом порядке: $\left \ < \begin& 4a+3y=17;\\ & 2a+7c+4y=10;\\ & -9a+8c+5y=25; \\ & 5a-c=-4. \end\right.$

Матрица системы имеет вид: $ A=\left( \begin 4 & 0 & 3 \\ 2 & 7 & 4\\ -9 & 8 & 5 \\ 5 & -1 & 0 \end \right)$. Матрица свободных членов: $B=\left( \begin 17 \\ 10 \\ 25 \\ -4 \end \right)$. При записи матрицы неизвестных помним о порядке следования неизвестных: $X=\left( \begin a \\ c \\ y \end \right)$. Итак, матричная форма записи заданной СЛАУ такова: $A\cdot X=B$. В развёрнутом виде:

$$ \left( \begin 4 & 0 & 3 \\ 2 & 7 & 4\\ -9 & 8 & 5 \\ 5 & -1 & 0 \end \right) \cdot \left( \begin a \\ c \\ y \end \right) = \left( \begin 17 \\ 10 \\ 25 \\ -4 \end \right) $$

Расширенная матрица системы такова: $\left( \begin 4 & 0 & 3 & 17 \\ 2 & 7 & 4 & 10\\ -9 & 8 & 5 & 25 \\ 5 & -1 & 0 & -4 \end \right) $.

Как видите, изменение порядка следования неизвестных равносильно перестановке столбцов матрицы системы. Но каким бы этот порядок расположения неизвестных ни был, он должен совпадать во всех уравнениях заданной СЛАУ.

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

Матричный метод решения СЛАУ: пример решения с помощью обратной матрицы

В данной статье мы расскажем о матричном методе решения системы линейных алгебраических уравнений, найдем его определение и приведем примеры решения.

Метод обратной матрицы — это метод, использующийся при решении СЛАУ в том случае, если число неизвестных равняется числу уравнений.

Найти решение системы n линейных уравнений с n неизвестными:

a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a n 1 x 1 + a n 2 x 2 + . . . + a n n x n = b n

Матричный вид записи: А × X = B

где А = а 11 а 12 ⋯ а 1 n а 21 а 22 ⋯ а 2 n ⋯ ⋯ ⋯ ⋯ а n 1 а n 2 ⋯ а n n — матрица системы.

X = x 1 x 2 ⋮ x n — столбец неизвестных,

B = b 1 b 2 ⋮ b n — столбец свободных коэффициентов.

Из уравнения, которое мы получили, необходимо выразить X . Для этого нужно умножить обе части матричного уравнения слева на A — 1 :

A — 1 × A × X = A — 1 × B .

Так как А — 1 × А = Е , то Е × X = А — 1 × В или X = А — 1 × В .

Обратная матрица к матрице А имеет право на существование только, если выполняется условие d e t A н е р а в е н н у л ю . Поэтому при решении СЛАУ методом обратной матрицы, в первую очередь находится d e t А .

В том случае, если d e t A н е р а в е н н у л ю , у системы имеется только один вариант решения: при помощи метода обратной матрицы. Если d e t А = 0 , то систему нельзя решить данным методом.

Пример решения системы линейных уравнений с помощью метода обратной матрицы

Решаем СЛАУ методом обратной матрицы:

2 x 1 — 4 x 2 + 3 x 3 = 1 x 1 — 2 x 2 + 4 x 3 = 3 3 x 1 — x 2 + 5 x 3 = 2

• Записываем систему в виде матричного уравнения А X = B , где

А = 2 — 4 3 1 — 2 4 3 — 1 5 , X = x 1 x 2 x 3 , B = 1 3 2 .

• Выражаем из этого уравнения X :

• Находим определитель матрицы А :

d e t A = 2 — 4 3 1 — 2 4 3 — 1 5 = 2 × ( — 2 ) × 5 + 3 × ( — 4 ) × 4 + 3 × ( — 1 ) × 1 — 3 × ( — 2 ) × 3 — — 1 × ( — 4 ) × 5 — 2 × 4 — ( — 1 ) = — 20 — 48 — 3 + 18 + 20 + 8 = — 25

d e t А не равняется 0, следовательно, для этой системы подходит метод решения обратной матрицей.

• Находим обратную матрицу А — 1 при помощи союзной матрицы. Вычисляем алгебраические дополнения А i j к соответствующим элементам матрицы А :

А 11 = ( — 1 ) ( 1 + 1 ) — 2 4 — 1 5 = — 10 + 4 = — 6 ,

А 12 = ( — 1 ) 1 + 2 1 4 3 5 = — ( 5 — 12 ) = 7 ,

А 13 = ( — 1 ) 1 + 3 1 — 2 3 — 1 = — 1 + 6 = 5 ,

А 21 = ( — 1 ) 2 + 1 — 4 3 — 1 5 = — ( — 20 + 3 ) = 17 ,

А 22 = ( — 1 ) 2 + 2 2 3 3 5 — 10 — 9 = 1 ,

А 23 = ( — 1 ) 2 + 3 2 — 4 3 — 1 = — ( — 2 + 12 ) = — 10 ,

А 31 = ( — 1 ) 3 + 1 — 4 3 — 2 4 = — 16 + 6 = — 10 ,

А 32 = ( — 1 ) 3 + 2 2 3 1 4 = — ( 8 — 3 ) = — 5 ,

А 33 = ( — 1 ) 3 + 3 2 — 4 1 — 2 = — 4 + 4 = 0 .

• Записываем союзную матрицу А * , которая составлена из алгебраических дополнений матрицы А :

А * = — 6 7 5 17 1 — 10 — 10 — 5 0

• Записываем обратную матрицу согласно формуле:

A — 1 = 1 d e t A ( A * ) T : А — 1 = — 1 25 — 6 17 — 10 7 1 — 5 5 — 10 0 ,

• Умножаем обратную матрицу А — 1 на столбец свободных членов В и получаем решение системы:

X = A — 1 × B = — 1 25 — 6 17 — 10 7 1 — 5 5 — 10 0 1 3 2 = — 1 25 — 6 + 51 — 20 7 + 3 — 10 5 — 30 + 0 = — 1 0 1

Ответ: x 1 = — 1 ; x 2 = 0 ; x 3 = 1