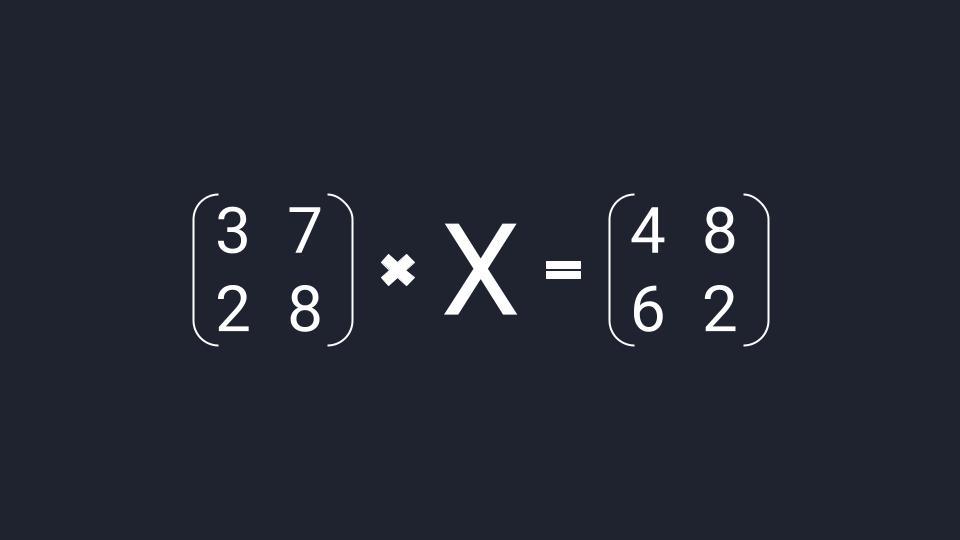Матричное уравнение x axb c

Решение матричных уравнений: теория и примеры

Решение матричных уравнений: как это делается

Матричные уравнения имеют прямую аналогию с простыми алгебраическими уравнениями, в которых присутствует операция умножения. Например,

где x — неизвестное.

А, поскольку мы уже умеем находить произведение матриц, то можем приступать к рассмотрению аналогичных уравнений с матрицами, в которых буквы — это матрицы.

Итак, матричным уравнением называется уравнение вида

где A и B — известные матрицы, X — неизвестная матрица, которую требуется найти.

Как решить матричное уравнение в первом случае? Для того, чтобы решить матричное уравнение вида A ⋅ X = B , обе его части следует умножить на обратную к A матрицу слева:

.

По определению обратной матрицы, произведение обратной матрицы на данную исходную матрицу равно единичной матрице: , поэтому

.

Так как E — единичная матрица, то E ⋅ X = X . В результате получим, что неизвестная матрица X равна произведению матрицы, обратной к матрице A , слева, на матрицу B :

.

Как решить матричное уравнение во втором случае? Если дано уравнение

то есть такое, в котором в произведении неизвестной матрицы X и известной матрицы A матрица A находится справа, то нужно действовать аналогично, но меняя направление умножения на матрицу, обратную матрице A , и умножать матрицу B на неё справа:

,

,

.

Как видим, очень важно, с какой стороны умножать на обратную матрицу, так как . Обратная к A матрица умножается на матрицу B с той стороны, с которой матрица A умножается на неизвестную матрицу X . То есть с той стороны, где в произведении с неизвестной матрицей находится матрица A .

Как решить матричное уравнение в третьем случае? Встречаются случаи, когда в левой части уравнения неизвестная матрица X находится в середине произведения трёх матриц. Тогда известную матрицу из правой части уравнения следует умножить слева на матрицу, обратную той, которая в упомянутом выше произведении трёх матриц была слева, и справа на матрицу, обратную той матрице, которая располагалась справа. Таким образом, решением матричного уравнения

.

Решение матричных уравнений: примеры

Пример 1. Решить матричное уравнение

.

Решение. Данное уравнение имеет вид A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A .

Сначала найдём определитель матрицы A :

.

Найдём алгебраические дополнения матрицы A :

.

Составим матрицу алгебраических дополнений:

.

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

.

Теперь у нас есть всё, чтобы найти матрицу, обратную матрице A :

.

Наконец, находим неизвестную матрицу:

Пример 2. Решить матричное уравнение

.

Пример 3. Решить матричное уравнение

.

Решение. Данное уравнение имеет вид X ⋅ A = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A .

Сначала найдём определитель матрицы A :

.

Найдём алгебраические дополнения матрицы A :

.

Составим матрицу алгебраических дополнений:

.

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

.

Находим матрицу, обратную матрице A :

.

Находим неизвестную матрицу:

До сих пор мы решали уравнения с матрицами второго порядка, а теперь настала очередь матриц третьего порядка.

Пример 4. Решить матричное уравнение

.

Решение. Это уравнение первого вида: A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A .

Сначала найдём определитель матрицы A :

.

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

.

Находим матрицу, обратную матрице A , и делаем это легко, так как определитель матрицы A равен единице:

.

Находим неизвестную матрицу:

Пример 5. Решить матричное уравнение

.

Решение. Данное уравнение имеет вид X ⋅ A = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A .

Сначала найдём определитель матрицы A :

.

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

.

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

.

Находим матрицу, обратную матрице A :

.

Находим неизвестную матрицу:

Пример 6. Решить матричное уравнение

.

Решение. Данное уравнение имеет вид A ⋅ X ⋅ B = C , то есть неизвестная матрица X находится в середине произведения трёх матриц. Поэтому решение следует искать в виде . Найдём матрицу, обратную матрице A .

Сначала найдём определитель матрицы A :

.

Найдём алгебраические дополнения матрицы A :

.

Составим матрицу алгебраических дополнений:

.

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

.

Находим матрицу, обратную матрице A :

.

Найдём матрицу, обратную матрице B .

Сначала найдём определитель матрицы B :

.

Найдём алгебраические дополнения матрицы B :

Составим матрицу алгебраических дополнений матрицы B :

.

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей B :

.

Находим матрицу, обратную матрице B :

.

Решение матричных уравнений

Финальная глава саги.

Линейная алгебра и, в частности, матрицы — это основа математики нейросетей. Когда говорят «машинное обучение», на самом деле говорят «перемножение матриц», «решение матричных уравнений» и «поиск коэффициентов в матричных уравнениях».

Понятно, что между простой матрицей в линейной алгебре и нейросетью, которая генерирует котов, много слоёв усложнений, дополнительной логики, обучения и т. д. Но здесь мы говорим именно о фундаменте. Цель — чтобы стало понятно, из чего оно сделано.

Краткое содержание прошлых частей:

• Линейная алгебра изучает векторы, матрицы и другие понятия, которые относятся к упорядоченным наборам данных. Линейной алгебре интересно, как можно трансформировать эти упорядоченные данные, складывать и умножать, всячески обсчитывать и находить в них закономерности.
• Вектор — это набор упорядоченных данных в одном измерении. Можно упрощённо сказать, что это последовательность чисел.
• Матрица — это тоже набор упорядоченных данных, только уже не в одном измерении, а в двух (или даже больше).
• Матрицу можно представить как упорядоченную сумку с данными. И с этой сумкой как с единым целым можно совершать какие-то действия. Например, делить, умножать, менять знаки.
• Матрицы можно складывать и умножать на другие матрицы. Это как взять две сумки с данными и получить третью сумку, тоже с данными, только теперь какими-то новыми.
• Матрицы перемножаются по довольно замороченному алгоритму. Арифметика простая, а порядок перемножения довольно запутанный.

И вот наконец мы здесь: если мы можем перемножать матрицы, то мы можем и решить матричное уравнение.

❌ Никакого практического применения следующего материала в народном хозяйстве вы не увидите. Это чистая алгебра в несколько упрощённом виде. Отсюда до практики далёкий путь, поэтому, если нужно что-то практическое, — посмотрите, как мы генерим Чехова на цепях Маркова.

Что такое матричное уравнение

Матричное уравнение — это когда мы умножаем известную матрицу на матрицу Х и получаем новую матрицу. Наша задача — найти неизвестную матрицу Х.

Шаг 1. Упрощаем уравнение

Вместо известных числовых матриц вводим в уравнение буквы: первую матрицу обозначаем буквой A, вторую — буквой B. Неизвестную матрицу X оставляем. Это упрощение поможет составить формулу и выразить X через известную матрицу.

Приводим матричное уравнение к упрощённому виду

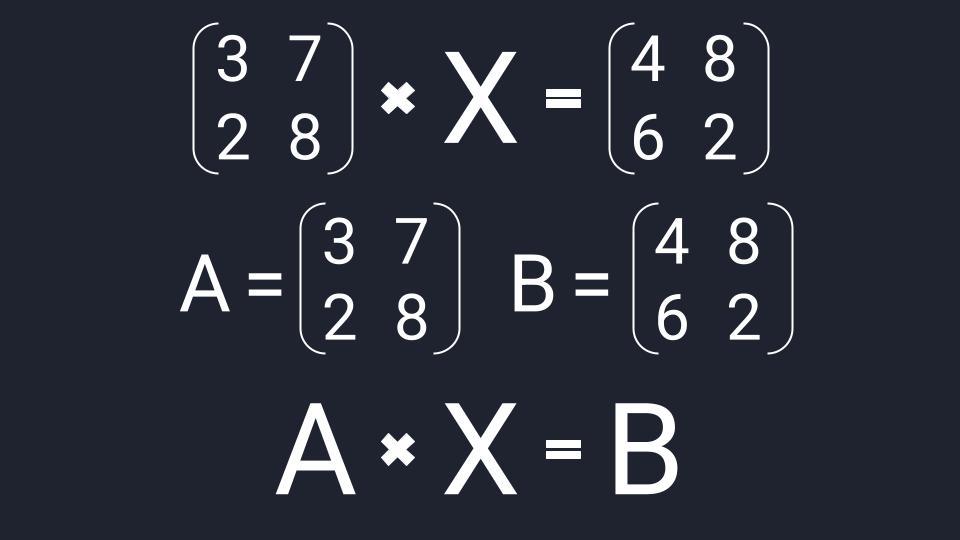
Шаг 2. Вводим единичную матрицу

В линейной алгебре есть два вспомогательных понятия: обратная матрица и единичная матрица. Единичная матрица состоит из нулей, а по диагонали у неё единицы. Обратная матрица — это такая, которая при умножении на исходную даёт единичную матрицу.

Можно представить, что есть число 100 — это «сто в первой степени», 100 1

И есть число 0,01 — это «сто в минус первой степени», 100 -1

При перемножении этих двух чисел получится единица:
100 1 × 100 -1 = 100 × 0,01 = 1.

Вот такое, только в мире матриц.

Зная свойства единичных и обратных матриц, делаем алгебраическое колдунство. Умножаем обе известные матрицы на обратную матрицу А -1 . Неизвестную матрицу Х оставляем без изменений и переписываем уравнение:

А -1 × А × Х = А -1 × В

Добавляем единичную матрицу и упрощаем запись:

А -1 × А = E — единичная матрица

E × Х = А -1 × В — единичная матрица, умноженная на исходную матрицу, даёт исходную матрицу. Единичную матрицу убираем

Х = А -1 × В — новая запись уравнения

После введения единичной матрицы мы нашли способ выражения неизвестной матрицы X через известные матрицы A и B.

💡 Смотрите, что произошло: раньше нам нужно было найти неизвестную матрицу. А теперь мы точно знаем, как её найти: нужно рассчитать обратную матрицу A -1 и умножить её на известную матрицу B. И то и другое — замороченные процедуры, но с точки зрения арифметики — просто.

Шаг 3. Находим обратную матрицу

Вспоминаем формулу и порядок расчёта обратной матрицы:

1. Делим единицу на определитель матрицы A.
2. Считаем транспонированную матрицу алгебраических дополнений.
3. Перемножаем значения и получаем нужную матрицу.

Собираем формулу и получаем обратную матрицу. Для удобства умышленно оставляем перед матрицей дробное число, чтобы было проще считать.

Третье действие: получаем обратную матрицу

Шаг 4. Вычисляем неизвестную матрицу

Нам остаётся посчитать матрицу X: умножаем обратную матрицу А -1 на матрицу B. Дробь держим за скобками и вносим в матрицу только при условии, что элементы новой матрицы будут кратны десяти — их можно умножить на дробь и получить целое число. Если кратных элементов не будет — дробь оставим за скобками.

Решаем матричное уравнение и находим неизвестную матрицу X. Мы получили кратные числа и внесли дробь в матрицу

Шаг 5. Проверяем уравнение

Мы решили матричное уравнение и получили красивый ответ с целыми числами. Выглядит правильно, но в случае с матрицами этого недостаточно. Чтобы проверить ответ, нам нужно вернуться к условию и умножить исходную матрицу A на матрицу X. В результате должна появиться матрица B. Если расчёты совпадут — мы всё сделали правильно. Если будут отличия — придётся решать заново.

👉 Часто начинающие математики пренебрегают финальной проверкой и считают её лишней тратой времени. Сегодня мы разобрали простое уравнение с двумя квадратными матрицами с четырьмя элементами в каждой. Когда элементов будет больше, в них легко запутаться и допустить ошибку.

Проверяем ответ и получаем матрицу B — наши расчёты верны

Ну и что

Алгоритм решения матричных уравнений несложный, если знать отдельные его компоненты. Дальше на основе этих компонентов математики переходят в более сложные пространства: работают с многомерными матрицами, решают более сложные уравнения, постепенно выходят на всё более и более абстрактные уровни. И дальше, в конце пути, появляется датасет из миллионов котиков. Этот датасет раскладывается на пиксели, каждый пиксель оцифровывается, цифры подставляются в матрицы, и уже огромный алгоритм в автоматическом режиме генерирует изображение нейрокотика:

научная статья по теме ЧИСЛЕННОЕ РЕШЕНИЕ МАТРИЧНОГО УРАВНЕНИЯ X – A B = C В САМОСОПРЯЖЕННОМ СЛУЧАЕ Математика

Цена:

Авторы работы:

Научный журнал:

Год выхода:

Текст научной статьи на тему «ЧИСЛЕННОЕ РЕШЕНИЕ МАТРИЧНОГО УРАВНЕНИЯ X – A B = C В САМОСОПРЯЖЕННОМ СЛУЧАЕ»

ЖУРНАЛ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ И МАТЕМАТИЧЕСКОЙ ФИЗИКИ, 2014, том 54, № 3, с. 371-374

ЧИСЛЕННОЕ РЕШЕНИЕ МАТРИЧНОГО УРАВНЕНИЯ X — AXB = C

В САМОСОПРЯЖЕННОМ СЛУЧАЕ

© 2014 г. Ю. О. Воронцов, X. Д. Икрамов

(119992 Москва, Ленинские горы, МГУ, ВМК) e-mail: vv@cs.msu.su, ikramov@cs.msu.su Поступила в редакцию 02.10.2013 г.

Предложены модификации алгоритма численного решения уравнения X — AXB = C для случая, когда это уравнение можно рассматривать как самосопряженное. Приведены числовые результаты, иллюстрирующие экономию времени и вычислительной работы, достигаемую посредством этих модификаций. Библ. 8. Фиг. 2.

Ключевые слова: матричное уравнение, сопряженный оператор, самосопряженность, полулинейный оператор, численный метод решения.

Дискретным уравнением Сильвестра, или уравнением Стейна, называется матричное уравнение

мы называем уравнениями типа Стейна. Черта над символом матрицы в уравнении (2) означает взятие поэлементного комплексного сопряжения. В уравнениях (1) и (2) A и B — квадратные матрицы, вообще говоря, различных порядков, m и п, а Xи C — матрицы размера m х п. В уравнениях (3) и (4) все четыре матрицы могут быть прямоугольными одного и того же размера m х п.

В [1]—[4] были установлены условия однозначной разрешимости матричных уравнений типа Стейна, а также предложены алгоритмы численного решения таких уравнений. В самосопряженном случае уравнения (1), (3) и (4) были рассмотрены в [5]—[7]. Настоящая статья посвящена методам решения уравнения (2) (также в самосопряженном случае).

Множество Mm, п(С) комплексных m х n-матриц мы интерпретируем как унитарное пространство со скалярным произведением

Сопоставим каждому из уравнений (1), (2) оператор, действующий в этом пространстве

Fa b : X ^ X — AXB, Ga b : X — X — AXB.

По аналогии уравнения

В [7] доказаны следующие теоремы.

Теорема 1. Пусть обе матрицы А и В ненулевые. Оператор /А, в тогда и только тогда является самосопряженным, когда

для некоторого комплексного числа а с модулем 1.

Теорема 2. Пусть обе матрицы А и В ненулевые. Оператор 0А в тогда и только тогда является самосопряженным, когда А и В одновременно симметричны либо кососимметричны.

Условия однозначной разрешимости и алгоритм решения уравнения (2) напоминаются в разд. 2. В разд. 3 описываются алгоритмы численного решения этого уравнения в самосопряженном случае. Результаты тестовых расчетов, обсуждаемые в разд. 4, показывают, какую экономию времени и вычислений дают эти алгоритмы по сравнению с методом, предназначенным для уравнения общего вида.

2. АЛГОРИТМ ДЛЯ УРАВНЕНИЯ ОБЩЕГО ВИДА В [4] была доказана следующая

Теорема 3. Уравнение (2) разрешимо единственным образом тогда и только тогда, когда единственным образом разрешимо уравнение Стейна

У — ААУВВ = С + АС В. (5)

При этом, если X—решение уравнения (2), то У= Хестьрешение уравнения (5).

Эта теорема указывает следующий путь к решению уравнения (2) в общем случае: сведение (2) к уравнению (5) и решение последнего уравнения стандартными методами.

3. САМОСОПРЯЖЕННОЕ УРАВНЕНИЕ

Опишем два способа решения уравнения (2) в самосопряженном случае. Мы будем называть их, соответственно, прямым алгоритмом и сведением к уравнению Стейна (5).

Согласно теореме 2, матричные коэффициенты А и В уравнения (2) одновременно симметричны либо кососимметричны. Рассмотрим симметричный случай. Разобьем алгоритм на четыре этапа.

1. Приведение матриц А и В к диагональной форме. Речь здесь идет об определении унитарных матриц и и Vтаких, что матрицы

диагональные. Средством вычисления указанных матриц служит разложение Такаги (см. [8, Следствие 4.4.4]), представляющее собой симметричный вариант сингулярного разложения.

2. Преобразование правой части. На этом этапе вычисляется матрица

Результатом первых двух этапов является замена уравнения (2) уравнением

Неизвестная матрица Усвязана с X соотношением

3. Решение уравнения (6). Это матричное уравнение есть диагональная система полулинейных уравнений относительно п2 коэффициентов у у матрицы У. Отсюда следует, что сложность этапа 3 составляет 0(п2) арифметических операций.

4. Возврат к исходной матрице X. Обращая соотношение (7), получаем

ЧИСЛЕННОЕ РЕШЕНИЕ МАТРИЧНОГО УРАВНЕНИЯ X — АХВ = С

0 500 1000 1500 2000 2500 3000

0 500 1000 1500 2000 2500 3000

Отметим, что в кососимметричном случае изменится преобразование матриц А и В. Посредством процесса, аналогичного разложению Такаги, они приводятся к квазидиагональным матрицам с блоками порядка 1 и 2. Сложность третьего этапа и в этом случае составляет 0(п2) арифметических операций.

Пусть выполнены условия теоремы 2. В этом случае коэффициенты АА = ±АА* и ВВ = ±В*В уравнения (5) будут эрмитовыми матрицами и, следовательно, для этого уравнения выполнены условия теоремы 1 (при а = 1). Таким образом, сводя уравнение (2) к уравнению (5), мы можем решать последнее, используя разработанный ранее алгоритм для решения уравнения Стейна в самосопряженном случае (см. [5]). Отметим, что при таком подходе нет необходимости различать симметричный и кососимметричный случаи.

Алгоритм для решения уравнения (2), описанный в разд. 2, был реализован в виде функции языка МаНаЪ 8Ипе. Алгоритмы для решения уравнения (2) из разд. 3 таким же образом были реализованы в виде функций 8ТНпе и 88Нпе.

В наших экспериментах мы интересовались ускорением, которое можно получить, решая самосопряженное уравнение (2) алгоритмами из разд. 3 вместо использования алгоритма для уравнения общего вида.

Были проведены три серии расчетов, в первой из которых использовалась функция 8Ипе, во второй — 8ТНпе, в третьей — 88Ипе. В каждой из серий матрицы А, В и С уравнения (2) генерировались как матрицы с псевдослучайными элементами, равномерно распределенными в круге радиусом 10 (при этом матрицы А и В строились как симметричные). Порядок п этих матриц возрастал от 50 до 2950 с шагом 100. Для каждого из этих значений п было измерено время работы программ 8Ипе, 8ТЦпе и 88Ипе: ^(п), ?2(п) и ?3(п), с усреднением по 10 однотипным уравнениям. Интерес представляют отношения ?х(п)/?2(п) и ?х(п)/?3(п), зависимость которых от порядка п показана на фиг. 1 и 2.

Важно отметить, что точность решения, вычисляемого алгоритмом 88Ипе, на несколько порядков хуже точности решения, которое находит 8ТЦпе. (Точность оценивалась посредством нормы разности точного и вычисленного решений.) Это различие связано с необходимостью выполнения четырех дополнительных матричных умножений при формировании уравнения (5).

1. ИкрамовХ.Д., Воронцов Ю.О. Матричное уравнение Х+ ЛХТВ = С: условия однозначной разрешимости

и алгоритм численного решения // Докл. АН. 2012. Т. 443. № 5. С. 545—548.

Сведение к уравнению Стейна

4. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ ЭКСПЕРИМЕНТОВ

2. Воронцов Ю.О., Икрамов Х.Д. Численное решение матричных уравнений вида X + AXTB = C// Ж. вычисл. матем. и матем. физ. 2013. Т. 53. № 3. С. 331—335.

3. Воронцов Ю.О. Модификация численного алгоритма для решения матричного уравнения X+ AXTB = C // Ж. вычисл. матем. и матем. физ. 2013. Т. 53. № 6. С. 853—856.

4. Zhou В., Lam J., Duan C.-R. Toward solution of matrix equation X = Af(X)B + C // Linear Algebra Appl. 2011. V. 435. № 11. P. 1370-1398.

5. Икрамов Х.Д., Воронцов Ю.О. Численное решение матричных уравнений Сильвестра в самосопряженном случае // Вестн. МГУ. 2014. № 2.

6. Воронцов Ю.О, ИкрамовХ.Д. Численное решение матричных уравнений типа Стейна в самосопряженном случае // Ж. вычисл. матем. и матем. физ. 2014. Т. 54. № 2.

7. Икрамов Х.Д. Условия самосопряженности матричных уравнений типа Стейна // Докл. АН. 2013. Т. 451. № 5. С. 498-500.

8. Хорн Р., Джонсон Ч. Матричный анализ. М.: Мир, 1989.

Для дальнейшего прочтения статьи необходимо приобрести полный текст. Статьи высылаются в формате PDF на указанную при оплате почту. Время доставки составляет менее 10 минут. Стоимость одной статьи — 150 рублей.