Матричные методы и операторные уравнения
Тема:«Векторно-матричные модели систем управления в непрерывном времени»
Понятие пространства состояний
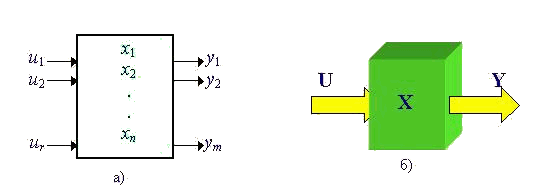
Современная теория автоматического управления оперирует с векторно-матричными моделями динамических систем. При этом рассматриваются в общем случае многомерные системы, т.е. системы произвольного порядка со многими входами и многими выходами, в связи, с чем широко используются векторно-матричные уравнения и аппарат векторной алгебры. Для получения векторно-матричной модели (ВММ) исследуемая динамическая система представляется в виде “черного ящика” с некоторым числом входных и выходных каналов (рис. 1.1, а).
Рис.1.1. Скалярное (а) и векторное (б) представления динамической системы в виде «черного ящика»
Все переменные, характеризующие систему, можно разделить на три группы.
1. Входные переменные или входные воздействия, генерируемые системами, внешними по отношению к исследуемой системе. Они характеризуются вектором входа.
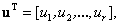
2. Выходные переменные, характеризующие реакцию системы на указанные входные воздействия. Представляются вектором выхода
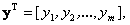
3. Промежуточные переменные, характеризующие внутреннее состояние системы, — переменные состояния, представляются вектором
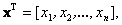
Таким образом, совокупность входов можно рассматривать как один обобщенный вход, на который воздействует вектор входа u, совокупность выходов как вектор y, а совокупность промежуточных координат, характеризующих состояние системы, — в виде вектора состояния x (см. рис. 1.1, б).
Состояние системы — это та минимальная информация о прошлом, которая необходима для полного описания будущего поведения (т.е. выходов) системы, если поведение ее входов известно.
Собственно система, ее входы и выходы — это три взаимосвязанных объекта, которые в каждой конкретной ситуации определяются соответственно математической моделью системы, заданием множеств входных и выходных переменных.
Решение задач анализа и синтеза связано с исследованием состояний системы, множество которых образует пространство состояний,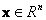
Векторно-матричные модели в непрерывном времени
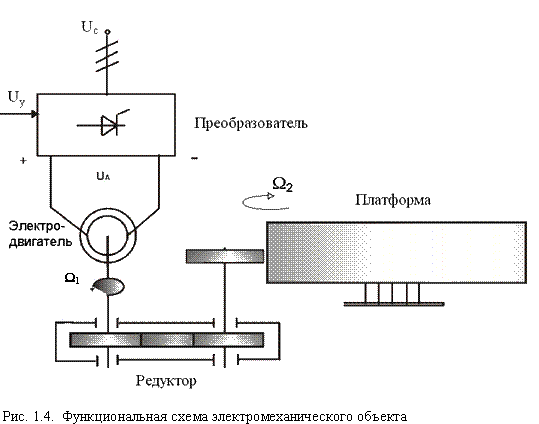
В общем случае динамическая система в непрерывном может быть описана парой матричных уравнений:
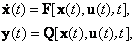 |
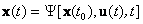 |
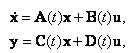 |
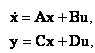 |
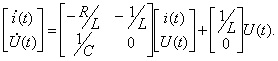 |
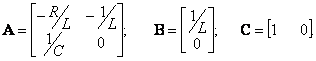 |
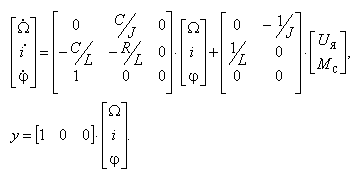 |
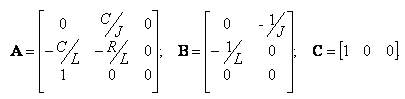 |
 |
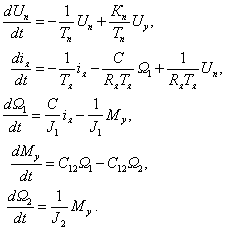 |
Если компонентами вектора состояния выбрать 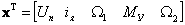
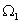
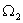
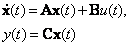 |
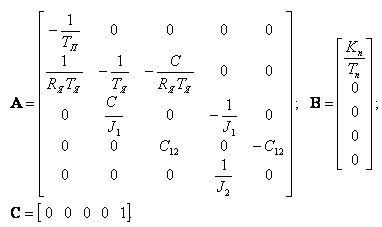 |
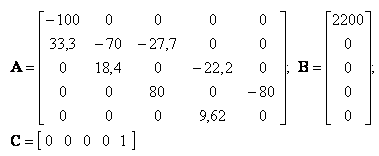 |
 | (1) |
Для решения системы линейных уравнений (1) матричным методом запишем ее матричном виде:
| Ax=b, | (2) |
  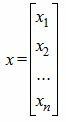 | (3) |
Мы будем предполагать, что матрица A имеет обратное, т.е. определитель матрицы A не равен нулю.
Умножим матричное уравнение (2) на обратную матрицу A −1 . Тогда
| A −1 Ax=A −1 b. | (4) |
Учитывая определение обратной матрицы, имеем A −1 A=E, где E— единичная матрица. Следовательно (4) можно записать так:
| Ex=A −1 b. | (4) |
или, учитывая, что Ex=x:
| x=A −1 b. | (5) |
Таким образом, для решения системы линейных уравнений (1) (или (2)), достаточно умножить обратную к A матрицу на вектор ограничений b.
Примеры решения системы линейных уравнений матричным методом
Пример 1. Решить следующую систему линейных уравнений матричным методом:
 |
Матричный вид записи системы линейных уравнений: Ax=b, где
 . . |
Найдем обратную к матрице A методом Жордана-Гаусса. С правой стороны матрицы A запишем единичную матрицу:
 . . |
Выбираем самый большой по модулю ведущий элемент столбца 1. Для этого заменяем местами строки 1 и 2:
 . . |
Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/3,-1/3 соответственно:
 . . |
Выбираем самый большой по модулю ведущий элемент столбца 2. Для этого заменяем местами строки 2 и 3:
 . . |
Исключим элементы 2-го столбца матрицы ниже главной диагонали. Для этого сложим строку 3 со строкой 2, умноженной на -24/51:
 . . |
Исключим элементы 3-го столбца матрицы выше главной диагонали. Для этого сложим строки 1, 2 со строкой 3, умноженной на 17/53, 85/159 соответственно:
 . . |
Исключим элементы 2-го столбца матрицы выше главной диагонали. Для этого сложим строку 1 со строкой 2, умноженной на -3/17:
 . . |
Делим каждую строку матрицы на ведущий элемент соответствующей строки:
 . . |
Отделяем правую часть матрицы. Полученная матрица является обратной матрицей к A :
 . . |
Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A−1b. Тогда
  . . |
 |
Пример 2. Решить следующую систему линейных уравнений матричным методом:
 . . |
Матричный вид записи системы линейных уравнений: Ax=b, где
 . . |
Найдем обратную к матрице A методом алгебраических дополнений. Вычислим определитель матрицы A :
 . . |
Вычислим все алгебраические дополнения матрицы A:
 , , |
 , , |
 , , |
 , , |
 , , |
 , , |
 , , |
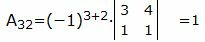 , , |
 . . |
Обратная матрица вычисляется из следующего выражения:
 |
где Aij − алгебраическое дополнение элемента матрицы A, находящиеся на пересечении i-ой строки и j-ого столбца, а Δ − определитель матрицы A.
Используя формулу обратной матрицы, получим:
 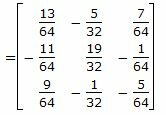 |
Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A −1 b. Тогда
http://zaochnik.com/spravochnik/matematika/issledovanie-slau/matrichnyj-metod-reshenija-slau/
http://matworld.ru/calculator/matrix-method-online.php
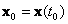 , дает вектор состояния системы
, дает вектор состояния системы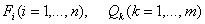 могут быть линейными комбинациями переменных состояния xi и входных переменных uq. При этом динамическая система описывается в векторно-матричной форме:
могут быть линейными комбинациями переменных состояния xi и входных переменных uq. При этом динамическая система описывается в векторно-матричной форме: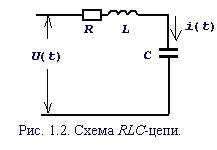
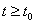 полностью определяется, если известны начальные значения
полностью определяется, если известны начальные значения 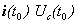 и входное напряжение U(t) при
и входное напряжение U(t) при 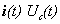 можно выбрать в качестве переменных состояния, то есть
можно выбрать в качестве переменных состояния, то есть 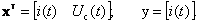
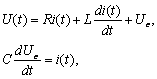
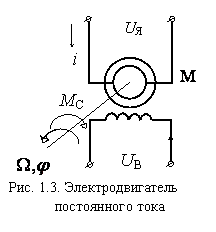
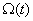 — скорости вращения ротора, тока якоря i(t), углового перемещения ротора
— скорости вращения ротора, тока якоря i(t), углового перемещения ротора 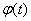 . При использовании знакомых зависимостей для электродвижущей силы
. При использовании знакомых зависимостей для электродвижущей силы 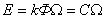 и вращающего момента двигателя
и вращающего момента двигателя 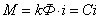 получим уравнение электрической цепи
получим уравнение электрической цепи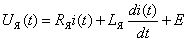
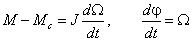
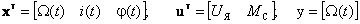 получим следующую векторно-матричную модель электродвигателя постоянного тока
получим следующую векторно-матричную модель электродвигателя постоянного тока
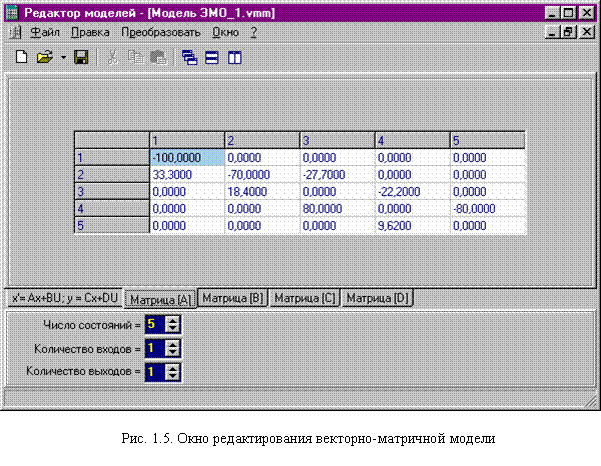
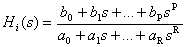
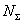 для описания этого объекта?
для описания этого объекта?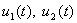 и одним выходом y(t) представлено следующим уравнением в операторной форме
и одним выходом y(t) представлено следующим уравнением в операторной форме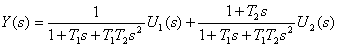
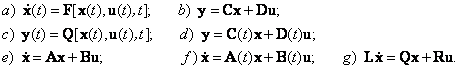
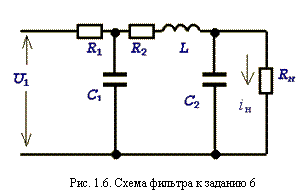
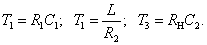
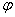 — угол поворота ротора электродвигателя,
— угол поворота ротора электродвигателя,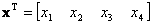 приведенной ниже векторно-матричной модели?
приведенной ниже векторно-матричной модели?