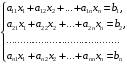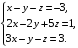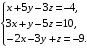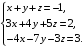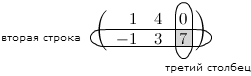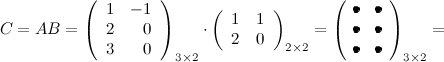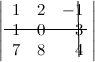Задания для практической работы по теме «Решение систем линейных уравнений с помощью обратной матрицы»
Данное задание предназначено для студентов второго курса специальности Компьютеные системы и комплексы по учебной дисциплине ЕН.01 Элементы высшей математики.
Просмотр содержимого документа
«Задания для практической работы по теме «Решение систем линейных уравнений с помощью обратной матрицы»»
Практическая работа № 6
Решение систем линейных уравнений с помощью обратной матрицы
Цель: научиться решать системы линейных уравнений с применением матричного метода.
В матричном методе решения систем линейных алгебраических уравнений вида:
которые в матричной форме записываются как А∙Х = В, где 
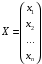
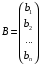
Решение системы линейных алгебраических уравнений матричным методом определяется по формуле X = A -1 ∙ B, т.е. решение находится с помощью обратной матрицы A -1 .
Практические задания для аудиторной работы
Решить систему линейных уравнений третьего порядка матричным методом.
а) 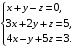
Решить систему линейных уравнений третьего порядка матричным методом.
а) 
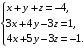
Решить систему линейных уравнений третьего порядка матричным методом.
а) 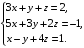
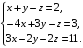
Решить систему линейных уравнений третьего порядка матричным методом.
а) 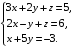

Решить систему линейных уравнений третьего порядка матричным методом.
а) 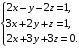

Какие системы называются эквивалентными?
Сформулируйте теорему Кронекера – Капелли.
Запишите систему линейных алгебраических уравнений в матричной форме.
Примеры решения задач с матрицами
Матрицы широко применяются в математике для компактной записи СЛАУ или систем дифференциальных уравнений. Тогда количество строк матрицы соответствует количеству уравнений системы, а количество столбцов равно количеству неизвестных. Матричный аппарат позволяет свести решение громоздких СЛАУ к компактным операциям над матрицами.
На практике, они позволяют не делать лишних операций и сократить время выполнения задач. Поэтому, будущим специалистам очень важно понять теорию матриц и научиться решать задачи с ними. Перед изучением примеров решения задач советуем изучить теоретический материал по матрицам, прочитать все определения и свойства. Список тем находится в правом меню.
Примеры по темам:
Матрицы: основные определения и понятия
Задание. Чему равен элемент $ a_ <23>$ матрицы $ A=\left( \begin
Решение. Находим элемент, который стоит на пересечении второй строки и третьего столбца:
Таким образом, $a_<23>=7$.
Ответ. $a_<23>=7$
Умножение матрицы на число
Теоретический материал по теме — умножение матрицы на число.
Задание. Пусть $A=\left( \begin
Ответ. $2 A=\left( \begin
Сложение и вычитание матриц
Теоретический материал по теме — сложение и вычитание матриц.
Задание. Найти матрицу $C=A-3 B$, если $A=\left( \begin
Умножение матриц
Теоретический материал по теме — умножение матриц.
Задание. Вычислить $A B$ и $B A$, если $A=\left( \begin
Решение. Так как $A=A_<3 \times 2>$ , а $B=B_<2 \times 2>$ , то произведение возможно и результатом операции умножения будет матрица $C=C_<3 \times 2>$ , а это матрица вида $C=\left( \begin
Вычисли элементы матрицы $C$ :
$ c_<11>=a_ <11>\cdot b_<11>+a_ <12>\cdot b_<21>=1 \cdot 1+(-1) \cdot 2=-1 $
$ c_<12>=a_ <11>\cdot b_<12>+a_ <12>\cdot b_<22>=1 \cdot 1+(-1) \cdot 0=1 $
$ c_<21>=a_ <21>\cdot b_<11>+a_ <22>\cdot b_<21>=2 \cdot 1+0 \cdot 2=2 $
$ c_<22>=a_ <21>\cdot b_<12>+a_ <22>\cdot b_<22>=2 \cdot 1+0 \cdot 0=2 $
$ c_<31>=a_ <31>\cdot b_<11>+a_ <32>\cdot b_<21>=3 \cdot 1+0 \cdot 2=3 $
$ c_<31>=a_ <31>\cdot b_<12>+a_ <32>\cdot b_<22>=3 \cdot 1+0 \cdot 0=3 $
Выполним произведения в более компактном виде:
Найдем теперь произведение $D=B A=B_ <2 \times 2>\cdot A_<3 \times 2>$. Так как количество столбцов матрицы $B$ (первый сомножитель) не совпадает с количеством строк матрицы $A$ (второй сомножитель), то данное произведение неопределенно. Умножить матрицы в данном порядке невозможно.
Ответ. $A B=\left( \begin
Транспонирование матрицы
Теоретический материал по теме — транспонирование матрицы.
Задание. Найти матрицу $A^
Минор и алгебраическое дополнение
Задание. Найти минор $M_<23>$ к элементу $a_<23>$ определителя $\left| \begin
Решение. Вычеркиваем в заданном определителе вторую строку и третий столбец:
Задание. Найти алгебраическое дополнение $A_<23>$ к элементу $a_<23>$ определителя $\left| \begin
Вычисление определителя
Задание. Вычислить определитель второго порядка $\left| \begin
Решение. $\left| \begin
Задание. Вычислить определитель $\left| \begin
Решение. $\left| \begin
$+3 \cdot 3 \cdot 1-(-1) \cdot 1 \cdot 1-3 \cdot(-2) \cdot 3-4 \cdot 3 \cdot(-2)=54$
Задание. Вычислить определитель $\left| \begin
Решение. Выполним следующие преобразования над строками определителя: из второй строки отнимем четыре первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель, равный данному.
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Задание. Вычислить определитель $\Delta=\left| \begin
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования будет выполнять проще, если элемент $a_<11>$ будет равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя, приведет к тому, что он сменит знак на противоположный:
Далее получим нули в первом столбце, кроме элемента $a_<11>$ , для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если диагональный элемент будет равен $\pm 1$ , то вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на противоположный знак определителя):
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом: к третьей строке прибавляем три вторых, а к четвертой — две вторых строки, получаем:
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под главной диагональю, а для этого к последней строке прибавляем третью:
Ответ. $\Delta=-80$
Нахождение обратной матрицы
Задание. Для матрицы $A=\left( \begin
Решение. Приписываем к заданной матрице $A$ справа единичную матрицу второго порядка:
От первой строки отнимаем вторую (для этого от элемента первой строки отнимаем соответствующий элемент второй строки):
От второй строки отнимаем две первых:
Первую и вторую строки меняем местами:
От второй строки отнимаем две первых:
Вторую строку умножаем на (-1), а к первой строке прибавляем вторую:
Итак, слева получили единичную матрицу, а значит матрица, стоящая в правой части (справа от вертикальной черты), является обратной к исходной.
Таким образом, получаем, что $A^<-1>=\left( \begin
Задание. Найти обратную матрицу для $A=\left( \begin
Решение. Шаг 1. Находим определитель: $\Delta=\left| \begin
Задание. Найти обратную матрицу к матрице $A=\left( \begin
Решение. Вычисляем определитель матрицы:
$\Delta=\left| \begin
$-1 \cdot(-1) \cdot 2-3 \cdot 1 \cdot 1-2 \cdot 0 \cdot(-1)=1+12+0+2-3+0=12 \neq 0$
Так как определитель не равен нулю, то матрица имеет обратную. Обратная матрица $A^<-1>$ к матрице $A$ находится по формуле:
Транспонируем эту матрицу (т.е. строки матрицы делаем столбцами с тем же номером):
Нахождение ранга матрицы
Теоретический материал по теме — нахождение ранга матрицы.
Решение. С помощью элементарных преобразований над ее строками приведем матрицу $A$ к ступенчатому виду. Для этого вначале от третьей строки отнимем две вторых:
От второй строки отнимаем четвертую строку, умноженную на 4; от третьей — две четвертых:
Ко второй строке прибавим пять первых, к третьей — три третьих:
Меняем местами первую и вторую строчки:
Далее четвертую и первую строки:
Ответ. $\operatorname
Задание. Найти ранг матрицы $A=\left( \begin
Решение. Минорами минимального порядка являются миноры первого порядка, которые равны элементам матрицы $A$ . Рассмотрим, например, минор $M_<1>=1 \neq 0$ . расположенный в первой строке и первом столбце. Окаймляем его с помощью второй строки и второго столбца, получаем минор $M_<2>^<1>=\left| \begin
так как содержит два пропорциональных столбца (первый и второй); второй минор
преобразуем следующим образом: к первой строке прибавим третью, а ко второй две третьих:
И так как первая и вторая строки пропорциональны, то минор равен нулю.
Таким образом, все окаймляющие миноры третьего порядка равны нулю. А, значит, ранг матрицы $A$ равен двум: $\operatorname
Ответ. $\operatorname
Занятие по теме «Матричные уравнения. Вычисление обратной матрицы»
Разделы: Математика
Цель: приобретение базовых знаний в области фундаментального раздела математики “Линейная алгебра” . Проверка усвоения знаний по вычислению обратной матрицы, нахождению алгебраических дополнений, дополнительного минора, вычислению определителей, решению матричных уравнений.
- развитие творческого профессионального мышления;
- развитие познавательной мотивации;
- овладение языком науки, приобретение навыков оперирования понятиями;
- овладение умениями и навыками постановки и решения задач;
- углубление теоретической и практической подготовки;
- развитие инициативы и самостоятельности студентов;
- формирование общих компетенций:
– организация собственной деятельности, исходя из цели и способов ее достижения, определенных руководителем;
– анализ рабочей ситуации, осуществление текущего и итогового контроля, оценка и коррекция собственной деятельности, ответственность за результаты своей работы;
– осуществление поиска информации, необходимой для эффективного выполнения профессиональных задач;
– использование информационно-коммуникационных технологий в профессиональной деятельности;
– работа в команде, эффективное общение с коллегами, руководством.
Обеспечение практического занятия:
Теоретический материал методической рекомендации к практической работе.
Учебники: Богомолов Н.В. “Математика”. – М.: Дрофа, 2009.
Омельченко В.П., Э.В. Курбатова. Математика, – Серия: Среднее профессиональное образование. – Ростов-на-Дону “Феникс”,2008-380с.
Индивидуальные карточки с вариантом практической работы.
Структура практического занятия.
1. Организационный этап.
Проверка готовности обучающихся к занятию.
2. Этап подготовки обучающихся к активному усвоению нового материала.
3. Этап усвоения новых знаний.
Формулирование темы занятия, пояснение связи темы с другими темами учебной дисциплины.
Проведение непосредственно занятия согласно тематике и в соответствии с рабочей программой дисциплины:
- Изучение теоретического материала по теме “Матричные уравнения. Вычисление обратной матрицы”.
4. Этап проверки понимания обучающимися нового материала.
- Примеры решения типовых заданий.
5. Этап закрепления нового материала.
- Выполнение практической работы по вычислению определителей, выполнению действий над матрицами, решению матричных уравнений.
6. Итоги занятия. Рефлексия.
7. Этап информирования обучающихся о домашнем задании.
Теоретические сведения и методические рекомендации по решению задач.
1. Изложение теоретического материала.
Определение. Квадратная матрица A -1 называется обратной к квадратной матрице A того же порядка, если AA -1 = A -1 A = E , где E – единичная матрица.
Утверждение. Квадратная матрица A имеет обратную матрицу тогда и только тогда, когда det A ≠ 0 .
Утверждение. Элементы cij обратной матрицы A -1 , если она существует, можно найти по формуле

Определение. Алгебраическим дополнение Aij элемента aij называется число, равное Aij = (–1) i+j Mij .
Определение. Дополнительным минором Mij элемента aij матрицы Ann называется определитель матрицы n-1-го порядка, полученный из матрицы Ann вычеркиванием i-ой строки и j-го столбца.
Однако, такой способ не удобен при нахождении обратных матриц больших порядков, поэтому обычно применяют следующую формулу:

Значение определителя: -10 + 6 – 40 = -44.
2. Закрепление теоретического материала, решение типовых задач.
№ 1. Найти матрицу C = A -1 обратную к A, если 
Решение. Прежде всего вычислим определитель матрицы A, чтобы убедиться в возможности существования обратной матрицы.
Следовательно, для матрицы A существует обратная матрица.
Воспользуемся формулой, выражающей элементы обратной матрицы через алгебраические дополнения к элементам транспонированной матрицы.
Для A T имеем 
Вычислим последовательно элементы Cij :
С учетом полученных данных, обратная к A матрица имеет вид
№ 2. Решить матричное уравнение A · X = B , где
Решение. Такое матричное уравнение, если определитель матрицы A отличен от нуля, удобно решать путем умножения обеих частей уравнения слева на матрицу A -1 . В этом случае для искомой матрицы получим A -1 · A · X = A -1 · B и поскольку A -1 · A = E , то X = A -1 · B .
Найдем теперь выражение для A -1 . Детерминант Δ матрицы A равен 4. Пользуясь формулами, определяющими элементы обратной матрицы, имеем

Учитывая последнее, для X получим:

3. Практическая работа обучающихся.
1. Найти матрицу обратную данной:
1. Найти матрицу обратную данной:
4. Подведение итогов практического занятия.
О чем сегодня на занятии шла речь?
С какими трудностями Вы столкнулись?
1. Сформулировать свойства определителя.
2. Какую матрицу называют обратной?
3. При каком условии существует обратная матрица?
4. Что называется алгебраическим дополнением матрицы?
5. Что называется минором матрицы?
6. В чем заключается метод построения обратной матрицы с использованием алгебраических дополнений.
5. Домашнее задание.
Учить определения, составить опорную схему конспекта. Выполнить упражнения:
1. Какая из матриц B, C, D является обратной к матрице A, если:
2. При каких λ существует A -1 , если:
3. Найти матрицу, обратную данной, если она существует:
http://www.webmath.ru/poleznoe/formules_6_16.php
http://urok.1sept.ru/articles/627735