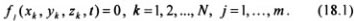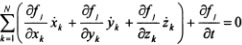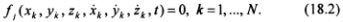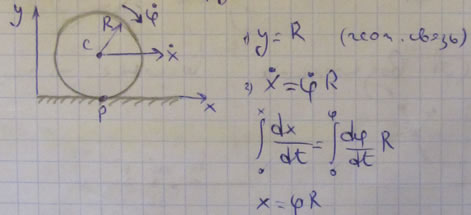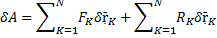Механические связи выражаются уравнениями то они называются

Please wait.

We are checking your browser. gufo.me

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6de77994cca51610 • Your IP : 85.95.188.35 • Performance & security by Cloudflare

СВЯ́ЗИ МЕХАНИ́ЧЕСКИЕ

СВЯ́ЗИ МЕХАНИ́ЧЕСКИЕ, ог­ра­ни­че­ния, на­ла­гае­мые на по­ло­же­ние и дви­же­ние ма­те­ри­аль­ных то­чек ме­ха­нич. сис­те­мы. Мо­гут осу­ще­ст­в­лять­ся с по­мо­щью не­под­виж­ных или со­вер­шаю­щих за­дан­ное дви­же­ние тел. При­ме­ром С. м. слу­жит опор­ная по­верх­ность, по ко­то­рой сколь­зит или ка­тит­ся те­ло. Ес­ли по­ло­же­ние $i$ -й ма­те­ри­аль­ной точ­ки по от­но­ше­нию к вы­бран­ной сис­те­ме от­счё­та оп­ре­де­ля­ют её де­кар­то­вы ко­ор­ди­на­ты $x_i$ , $y_i$ , $z_i$ ( $i=1,…, n$ , где $n$ – чис­ло то­чек сис­те­мы), то С. м. мо­гут быть вы­ра­же­ны в ви­де $$f(x_1, y_1, z_1. x_n,y_n,z_n,\dot x_1, \dot y_1, \dot z_1. \dot x_n, \dot y_n, \dot z_n, t) \leqslant 0, \tag<*>$$ где $\dot x_i$ , $\dot y_i$ , $\dot z_i$ – про­из­вод­ные ко­ор­ди­нат по вре­ме­ни $t$ . Та­кие С. м. на­ла­га­ют ог­ра­ни­че­ния на ко­ор­ди­на­ты и ско­ро­сти то­чек сис­те­мы и на­зы­ва­ют­ся ки­не­ма­ти­че­ски­ми. Ес­ли вы­ра­же­ние $(*)$ пред­став­ля­ет со­бой ра­вен­ст­во, ко­то­рое уда­ёт­ся про­ин­тег­ри­ро­вать и пред­ста­вить в ви­де $φ(x_i, y_i, z_i, t)=0$ , то та­кая С. м. (на­зы­вае­мая гео­мет­ри­че­ской или го­ло­ном­ной) по­зво­ля­ет со­кра­тить чис­ло па­ра­мет­ров, опи­сы­ваю­щих со­стоя­ние дви­же­ния сис­те­мы. Не­ин­тег­ри­руе­мое ра­вен­ст­во $(*)$ за­да­ёт не­го­ло­ном­ную ме­ха­ни­че­скую связь.

Механические связи выражаются уравнениями то они называются

Связи и их классификация.

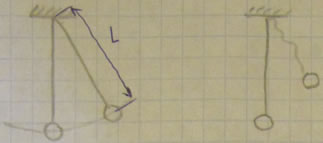
Связь называется удерживающей (двухсторонней), если она описывается уравнением (равенством). Голономную стационарную удерживающую связь, наложенную на материальную точку, можно представить в виде двух бесконечно близких одинаковых поверхностей, между которыми только и может находиться точка. Неудерживающая (односторонняя) связь описывается неравенством. Например, если математический маятник представляет собой тонкий стержень длиной l, вращающийся вокруг неподвижной оси и к свободному концу которого прикреплен груз (материальная точка), то связь для груза будет удерживающая. Если же груз прикреплен к свободному концу нерастяжимой нити длиной l. то связь будет неудерживающая, поскольку груз может находиться как на поверхности сферы радиусом l, так и внутри нее.

Механическая система, точки которой могут занимать любое положение в пространстве и иметь любые скорости, называется свободной. Например, свободной системой является космический аппарат, движущийся по орбите вокруг Земли. Его движение не ограничено другими телами и поэтому, прикладывая к аппарату соответствующие силы, можно изменять траекторию его центра масс и поворачивать аппарат вокруг центра масс. Если на координаты и скорости точек системы наложены ограничения, то система называется несвободной, а ограничения называются связями. Механические связи реализуются в виде различных устройств или тел (стержни, нити, шарниры и т. п.). Аналитически связь описывается уравнением вида: .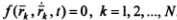

Ограничивая движение механической системы, связи действуют на ее точки посредством сил, которые называются реакциями
связей. При изучении равновесия и движения механических систем методами аналитической механики применяется принцип
освобождения (аксиома о связях). Этот принцип состоит в том, что любую систему можно рассматривать как свободную, приложив к ее точкам реакции, соответствующие отброшенным связям.

Связи называются галономными, если они описываются уравнениями вида:

Такие связи накладывают ограничения на координаты точек, а значит, на положение системы в пространстве. Это так называемые геометрические связи. Вместе с тем голономные связи накладывают ограничения и на скорости точек системы. Соответствующие условия получаются в результате дифференцирования уравнений (18.1) по времени:

Голономные связи могут описываться и дифференциальными уравнениями, однако последние обязательно должны быть интегрируемыми.

Неголономными называются связи, которые описываются уравнениями вида:

Уравнения (18.2), в отличие от уравнений голономных связей, не могут быть проинтегрированы независимо от дифференциальных уравнений движения системы. Неголономные связи накладывают ограничения (18.2) на скорости точек, поэтому их называют кинематическими.

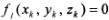
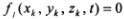
Связи подразделяются на стационарные и нестационарные в зависимости от того, входит в явном виде время в уравнение связи или нет. Связь, уравнение которой имеет вид , является голономной и стационарной. Для голономной нестационарной связи уравнение будет таким: .

Например, жесткий стержень длиной l, прикрепленный к неподвижной опоре, является стационарной связью для материальной точки, находящейся на его свободном конце. Уравнение связи в декартовой системе координат, начало которой совпадает с точкой закрепления стержня, имеет вид .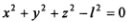

(При вращении стержня вокруг опоры точка находится на сфере радиусом l.) Если длина стержня изменяется по заданному закону, то связь является нестационарной и ее уравнение .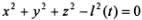

Связь называется удерживающей (двухсторонней), если она описывается уравнением (равенством). Голономную стационарную удерживающую связь, наложенную на материальную точку, можно представить в виде двух бесконечно близких одинаковых поверхностей, между которыми только и может находиться точка. Неудерживающая (односторонняя) связь описывается неравенством. Например, если математический маятник представляет собой тонкий стержень длиной l, вращающийся вокруг неподвижной оси и к свободному концу которого прикреплен груз (материальная точка), то связь для груза будет удерживающая. Если же груз прикреплен к свободному концу нерастяжимой нити длиной l. то связь будет неудерживающая, поскольку груз может находиться как на поверхности сферы радиусом l, так и внутри нее.

Из лекций:

Связи — условия, ограничивающие свободу перемещения материальной точки.

f(x,y,z,x · ,y · ,z · ,x · · ,y · · ,z · · ,t)=0

Классификация связей:

1) Геометрические связи.

2) Кинематические связи.

a) интегрируемые; (геометрические, интегрируемые кинематические = голономные)

б) неинтегрируемые; (геометрические, неинтегрируемые кинематические = неголономные)

3) Стационарная связь (склерономная).

Если t входит в уравнение явным образом, то связь нестационарная (реономная).

4) Освобождающие и неосвобождающие связи.

(неосвобождающая связь) ; (освобождающая связь)

x 2 +y 2 +z 2 =l 2 ; x 2 +y 2 +z 2 2

5) Идеальные и реальные связи.

Возможная работа — элементраная работа силы на возможном перемещении.

dA=Fdr — элементарная работа силы (F и r — векторы)

Если у какой-то связи 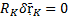(R_K тоже вектор), то связь называется идеальной.

Если вся сумма 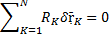, то механическая система с идеальными связями.

Реальные связи: .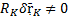

Примеры идеальных связей: внутренние связи в абсолютно твердых телах; абсолютно гладкие поверхности; шарниры без трения; нерастяжимые нити; закрепленные точки; качение без скольжения.

Примеры реальных связей: шероховатая поверхность; шарниры с трением; упругие растяжимые нити; пружины; качение с проскальзыванием.

Замечание: всякую реальную связь можно сделать идеальной.