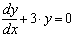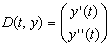методами Эйлера и Рунге-Кутта в системе MathCAD
Построение решений обыкновенных дифференциальных уравнений
Решение дифференциального уравнения 1-го порядка


Простой метод Эйлера реализуется применением на каждом шаге вычислений следующих итерационных выражений:
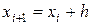
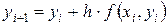
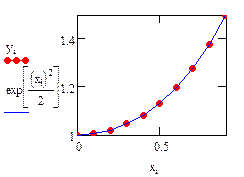
Рассмотрим реализацию метода в MathCADна примере уравнения:
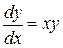
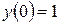
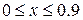
Аналитическое решение известно и имеет вид:

Краткие сведения о составлении программ в MathCAD
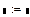
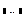
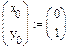
Графиквставляется командой Insert→ Graph→ X-YPlotили клавишей «@».
Для удобства в работе рекомендуется отключить автоматическое вычисление, убрав галочку с опции меню Tools→ Calculate→ AutomaticCalculation. Тогда расчет не будет выполняться в ходе набора программы, а запуститься только после нажатия кнопки Calculate, расположенной на панели инструментов (в виде значка 
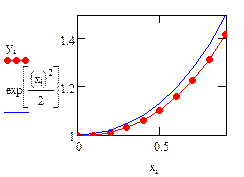
Ниже приведена расчетная программа. Повторите её. Получите графики с тем же форматом линий. Формат линий графика можно изменить, открыв с помощью ПК мыши контекстное меню и выбрав Format… → Traces.
Программа для простого метода Эйлера
 |
| Шаг изменения x |
 |
| Число шагов |
 |
| Функция, определяющая производную |
 |
| Задание цикла |
 |
| Задание начальных условий |
 |
| Итерационные уравнения |
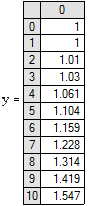
| Результаты решения: |
 |
 |
 |
 |
Следующая программа реализует модифицированный метод Эйлера. Отличие от простого метода заключается в итерационных уравнениях.
Программа для модифицированного метода Эйлера
 |
| Шаг изменения x |
 |
| Число шагов |
 |
| Функция, определяющая производную |
 |
| Задание цикла |
 |
| Задание начальных условий |
| Итерационные уравнения |
 |
| Результаты решения: |
 |
 |
 |
 |
Метод Рунге-Кутта 4-го порядка используется в тех случаях, когда необходима высокая точность расчетов, недостигаемая методами Эйлера.
Программа для метода Рунге-Кутта
 |
| Шаг изменения x |
 |
| Число шагов |
 |
| Функция, определяющая производную |
| Задание коэффициентов k1, k2, k3, k4 как функций пользователя: |
 |
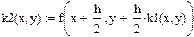 |
 |
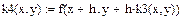 |
 |
| Усредненная функция |
 |
| Задание цикла |
 |
| Задание начальных условий |
 |
| Итерационные уравнения |
| Результаты решения: |
 |
 |
 |
 |
Решение дифференциальных уравнений 2-го порядкаметодом Рунге-Кутта.
Подход к реализации метода основан на использовании дополнительной функции 


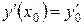
Преобразуем задачу к системе из двух уравнений:


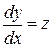

Тогда получим следующее обобщение итерационной схемы:



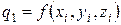
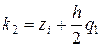




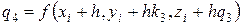
Отметим, что значения на каждом следующем шаге рассчитываются по значениям, полученным на предыдущем. Кроме того, использованы прежние правила «взвешивания» коэффициентов при усреднении.
Пример математической модели с дифференциальным уравнением 2-го порядка
Рассмотрим уравнение колебательного процесса при наличии внешнего периодического воздействия:

где t– время, и искомой является зависимость 
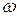
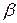
Если 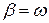

где Aи 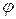
Когда 

В этом случае колебательный процесс слагается из собственных колебаний с частотой 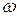
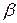
Моделирование резонансных колебаний
Методом Рунге-Кутта найдем решение задачи:

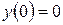


Согласно изложенной выше теории, аналитическое решение уравнения имеет вид:
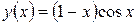
Ниже приведен алгоритм расчета и его реализация в MathCAD.
Программа расчета резонансных колебаний методом Рунге-Кутта
 |
| Шаг изменения x |
 |
| Число шагов |
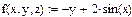 |
| Функция в системе уравнений dy/dx = z и dz/dx = f(x,y,z) |
| Задание коэффициентов как функций пользователя: |
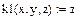 |
 |
 |
 |
 |
 |
 |
 |
| Усредненные функции: |
 |
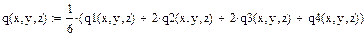 |
 |
| Задание цикла |
 |
| Задание начальных условий |
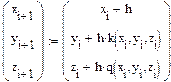 |
| Итерационные уравнения |
 |
| Результаты решения: |
Задание для самостоятельного выполнения
Найти решение уравнения вынужденных колебаний:

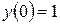
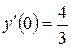
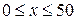
Решение представить в виде графика. Для сравнения привести и график точного решения (также как это было сделано для резонансных колебаний).
Дифференциальные уравнения в MathCad
Дифференциальные уравнения достаточно часто используются для того, чтобы описать значение часто меняющихся процессов. Сначала обратим внимание на самое стандартное уравнение данного типа.
Решение данного уравнения будет представлено следующим образом.
И это решение отличается максимально точным. Кроме того, оно отличается отменной результативностью. Жаль, что многие дифференциальные уравнения нереально решить при помощи аналитики. Мы часто вынуждены прибегать к численным методикам.
Метод Эйлера
Этот метод отличается максимальным удобством и простотой для решения уравнений дифференциального типа. Его достаточно легко понять и реализовать в сфере программирования.
Постепенно проследим изменения
Сравниваем результативность и правильный ответ
Необходимо учитывать, что методика Эйлера в некоторой степени отличается от точного решения задачи. И чем выше аргумент, тем внушительнее оказывается полученная разница. Чтобы свести к минимуму ошибку, нужно увеличить количество шагов.
Блок решения ОДУ
Mathcad вмещает в себя все самые важные опции для решения уравнения дифференциального типа. В данном уроке мы обратим внимание на самую важную функцию такого типа. Она характеризуется максимальной точностью и простотой использования. Методика сочетает пользование блоком решения и опцией odesolve(). Перед решением устанавливаем такие параметры:
Каждое вхождение переменной с в блок решения представляется как функция независимой переменной.
Данный метод во многом похож на принципы аналитического решения. Точно такой же результат удается получить после записи производной через штрих (Ctrl+’)
Сердце и артерии
Функционирование сердца и артерий во многом похожи на работу насоса. Они оба могут расшириться и сжаться, а клапаны перегоняют жидкость исключительно в одном направлении.
Пульсирование потока можно снизить, расширяя и сжимая стенки артерии.
Перепады давления возле легких достаточно низкие. Давайте установим, что повышенное давлении в точках А и В равняется нулю. Центральный элемент – это артерия, которая может изменяться в объемах.
Допустим, что объемы сердца могут изменяться в соответствии с особенностями синусоидального закона. Однако впырск крови происходит исключительно во время положительных полуволн.
График для восьми ударов:
Средний поток представляет собой интеграл объема, который задействован при одном ударе и поделен на его продолжительность.
Расширение артерий прямо зависит от общей эластичности стенок и особенностей их строений. Однако мы в математических целях предположим, будто объем прямо зависит от превышения давления.
Чем выше эластичность стенки, тем больше оказывается значение k. Установим ему три значения.
Баланс объемов артерий:
Вышеуказанная формула приводит к таковым результатам:
Данную функцию можно решить примерно так же, как и предыдущую. Единственное различие состоит в том, что k будет перенесено в блок решения уже в качестве параметра.
Теперь конвертируем решения.
Максимальные показания давления прямо зависят от уровня эластичности давления. Чем она выше, тем ниже оказывается само давление.
Так, вышеуказанный пример потребовал использование всего одного уравнения первого порядкового уровня. Однако программа Маткад не ограничивается данным функционалом.
Уважаемые пользователи, хотим Вас проинформировать о том, что некоторые антивирусные программы и браузеры ложно срабатывают на дистрибутив программы MediaGet, считая его зараженным. Данный софт не содержит никаких вредоносных программ и вирусов и многие из антивирусов просто Вас предупреждают, что это загрузчик (Downloader). Если хотите избежать подобных проблем, просто добавьте MediaGet в список доверенных программ Вашей антивирусной программы или браузера.
Выбрав нужную версию программы и кликнув ссылку, Вам на компьютер скачивается дистрибутив приложения MediaGet, который будет находиться в папке «Загрузки» для Вашего браузера. Находим этот файл с именем программы и запускаем его. И видим первый этап установки. Нажимаем унопку «Далее»
Далее Вам предлагается прочитать и одобрить лицензионное соглашение. Нажимаем кнопку «Принимаю»
В следующем окне Вам предлагается бесплатное полезное дополнительное программоное обеспечение, будь то антивирус или бразуер. Нажимаем кнопку «Принимаю». Также Вы можете отказаться от установки дополнительного ПО, нажав кнопку «Отклоняю»
Далее происходит процесс установки программы. Вам нужно выбрать папку, в которую будут скачиваться нужные Вам файлы.
Происходит завершение установки. Программа автоматически открывается и скачивает нужные Вам исходные файлы.
Обратите внимание, что предоставляемое программное обеспечение выкладывается исключительно для личного использования и ознакомления. Все файлы, доступные для скачивания, не содержат вирусов и вредоносных программ.
Метод эйлера для решения дифференциальных уравнений маткад
При решении дифференциального уравнения искомой величиной является функция. Для ОДУ неизвестная функция — функция одной переменной. Дифференциальные уравнения в частных производных — это дифференциальные уравнения, в которых неизвестной является функция двух или большего числа переменных. Mathcad имеет ряд встроенных функций, предназначенных для решения ОДУ. Каждая из этих функций предназначена для численного решения дифференциального уравнения. В результате решения получается матрица, содержащая значения функции, вычисленные на некотором множестве точек (на некоторой сетке значений). Для каждого алгоритма, который используется при решении дифференциальных уравнений, Mathcad имеет различные встроенные функции. Несмотря на различные методы поиска решения, каждая из этих функций требует, чтобы были заданы по крайней мере следующие величины, необходимые для поиска решения:
- Начальные условия.
- Набор точек, в которых нужно найти решение.
- Само дифференциальное уравнение, записанное в некотором специальном виде, который будет детально описан в этой главе.
В этом разделе описано, как решить ОДУ, используя функцию rkfixed. Раздел начинается с примера того, как решить простейшее дифференциальное уравнение первого порядка. Затем будет показано, как можно решать дифференциальные уравнения более высокого порядка.
Дифференциальные уравнения первого порядка
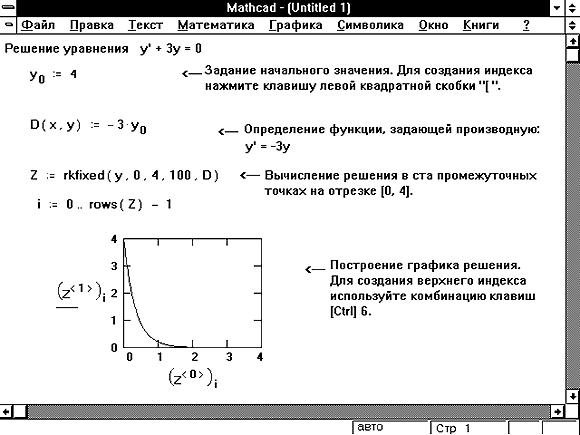
Дифференциальное уравнение первого порядка — это уравнение, которое не содержит производных выше первого порядка от неизвестной функции. На Рисунке 1 показан пример того, как решить относительно простое дифференциальное уравнение:
с начальными условиями: y(0) = 4
Функция rkfixed на Рисунке 1 использует для поиска решения метод Рунге-Кутты четвертого порядка. В результате решения получается матрица, имеющая два следующих столбца:
- Первый столбец содержит точки, в которых ищется решение дифференциального уравнения.
- Второй столбец содержит значения найденного решения в соответствующих точках.
Рисунок 1: Решение дифференциального уравнения первого порядка.
Функция rkfixed имеет следующие аргументы:
| y = | Вектор начальных условий размерности n, где n — порядок дифференциального уравнения или число уравнений в системе (если решается система уравнений). Для дифференциального уравнения первого порядка, как, например, для уравнения, приведенного на Рисунке 1, вектор начальных значений вырождается в одну точку y0 = y(x1). |
| x1, x2 = | Граничные точки интервала, на котором ищется решение дифференциальных уравнений. Начальные условия, заданные в векторе y, — это значение решения в точке x1. |
| npoints = | Число точек (не считая начальной точки), в которых ищется приближенное решение. При помощи этого аргумента определяется число строк (1 + npoints) в матрице, возвращаемой функцией rkfixed. |
| D (x, y) = | Функция, возвращающая значение в виде вектора из n элементов, содержащих первые производные неизвестных функций. |
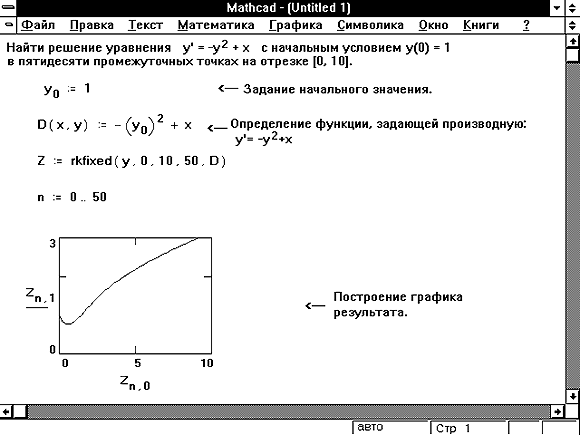
Наиболее трудная часть решения дифференциального уравнения состоит в определении функции D(x, y), которая содержит вектор первых производных от неизвестных функций. В примере, приведенном на Рисунке 1, было достаточно просто разрешить уравнение относительно первой производной , и определить функцию D(x, y). Иногда, особенно в случае нелинейных дифференциальных уравнений, это может быть трудно. В таких случаях иногда удаётся разрешить уравнение относительно в символьном виде и подставить это решение в определение для функции D(x, y). Используйте для этого команду Решить относительно переменной из меню Символика.
Рисунок 2: Более сложный пример, содержащий нелинейное дифференциальное уравнение.
Дифференциальные уравнения второго порядка
Как только Вы научились решать дифференциальное уравнение первого порядка, можно приступать к решению дифференциальных уравнений более высокого порядка. Мы начнем с дифференциального уравнения второго порядка. Основные отличия от уравнения первого порядка состоят в следующем:
- Вектор начальных условий y теперь состоит из двух элементов: значений функции и её первой производной в начальной точке интервала x1.
- Функция D(t, y) является теперь вектором с двумя элементами:
Пример, приведенный на Рисунке 3, показывает, как решить следующее дифференциальное уравнение второго порядка:
Рисунок 3: Решение дифференциального уравнения второго порядка.
Уравнения более высокого порядка
Методика решения дифференциальных уравнений более высокого порядка является развитием методики, которая применялась для решения дифференциальных уравнений второго порядка. Основное различие состоит в следующем:
- Вектор начальных значений y теперь состоит из n элементов, определяющих начальные условия для искомой функции и ее производных y, y’ , y». y (n-1)
- Функция D является теперь вектором, содержащим n элементов:
Пример, приведенный на Рисунке 4, показывает, как решить следующее дифференциальное уравнение четвертого порядка:
с начальными условиями:
Рисунок 4: Решение дифференциального уравнения более высокого порядка.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
http://stylingsoft.com/sapr/mathcad/uroki-mathcad/1433-differentsialnye-uravneniya-v-mathcad
http://old.exponenta.ru/soft/MathCAD/usersguide/chapter16/16_1.asp