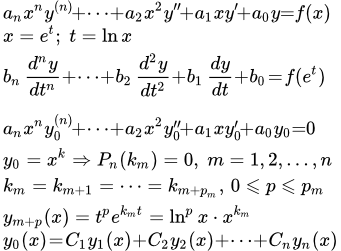Метод эйлера для решения дифференциальных уравнений с постоянными

Дифференциальное уравнение Эйлера и методы его решения

Более общее уравнение Эйлера имеет вид:
.
Это уравнение подстановкой t = ax+b приводится к более простому виду, которое мы и будем рассматривать.

Приведение дифференциального уравнения Эйлера к уравнению с постоянными коэффициентами.

Рассмотрим уравнение Эйлера:
(1) .
Оно сводится к линейному уравнению с постоянными коэффициентами подстановкой:
x = e t .
Действительно, тогда
;
;
;

;
;
.

Таким образом, множители, содержащие x m , сокращаются. Остаются члены с постоянными коэффициентами. Однако на практике, для решения уравнений Эйлера, можно применять методы решения линейных ДУ с постоянными коэффициентами без использования указанной выше подстановки.

Решение однородного уравнения Эйлера

Рассмотрим однородное уравнение Эйлера:
(2) .
Ищем решение уравнения (2) в виде
.
;
;
.
.
Подставляем в (2) и сокращаем на x k . Получаем характеристическое уравнение:
.
Решаем его и получаем n корней, которые могут быть комплексными.

Рассмотрим действительные корни. Пусть k_i – кратный корень кратности m . Этим m корням соответствуют m линейно независимых решений:
.

Рассмотрим комплексные корни. Они появляются парами вместе с комплексно сопряженными. Пусть k_i – кратный корень кратности m . Выразим комплексный корень k_i через действительную и мнимую части:
.
Этим m корням и m комплексно сопряженным корням соответствуют 2 m линейно независимых решений:
;
;
.
.

После того как получены n линейно независимых решений, получаем общее решение уравнения (2):
(3) .

Примеры

Решение неоднородного уравнения Эйлера

Рассмотрим неоднородное уравнение Эйлера:
.
Метод вариации постоянных (метод Лагранжа) также применим и к уравнениям Эйлера.

Сначала мы решаем однородное уравнение (2) и получаем его общее решение (3). Затем считаем постоянные функциями от переменной x . Дифференцируем (3) n – 1 раз. Получаем выражения для n – 1 производных y по x . При каждом дифференцировании члены, содержащие производные приравниваем к нулю. Так получаем n – 1 уравнений, связывающих производные . Далее находим n -ю производную y . Подставляем полученные производные в (1) и получаем n -е уравнение, связывающее производные . Из этих уравнений определяем . После чего интегрируя, получаем общее решение уравнения (1).

Пример

Неоднородное уравнение Эйлера со специальной неоднородной частью

Рассмотрим уравнение Эйлера со специальной неоднородной частью:
(4)
,
где – многочлены от степеней и , соответственно.

Наиболее простой способ решения такого уравнения заключается в том, чтобы сделать подстановку
,
и решать линейное уравнение с постоянными коэффициентами со специальной неоднородной частью.

Автор: Олег Одинцов . Опубликовано: 14-08-2013 Изменено: 24-10-2020

Интегрирование однородных линейных систем ДУ
с постоянными коэффициентами. Метод Эйлера

Линейной однородной системой с постоянными коэффициентами называется система дифференциальных уравнений вида

где коэффициенты — постоянные, а — искомые функции от .

Систему (1) можно коротко записать в виде одного матричного уравнения

называется частным решением уравнения (2) в интервале , если выполняется тождество

Система частных решений

(здесь в записи нижний индекс указывает номер решения, а верхний — номер функции в решении) называется фундаментальной на интервале , если ее определитель Вронского

Теорема. Если система частных решений однородного уравнения (2) является фундаментальной, то общее решение этого уравнения имеет вид

где — произвольные постоянные.

Линейные системы можно интегрировать различными способами, рассмотренными ранее, например методом исключения, путем нахождения интегрируемых комбинаций и т.д.

Для интегрирования однородных линейных систем с постоянными коэффициентами применяется также метод Эйлера .

Рассмотрим этот метод в применении к системе трех линейных дифференциальных уравнений:

Решение системы (3) ищем в виде

Подставляя (4) в (3) и сокращая на , получаем систему уравнений для определения и

Система (5) имеет ненулевое решение, когда ее определитель равен нулю,

Уравнение (6) называется характеристическим .

А. Пусть корни и характеристического уравнения — вещественные и различные . Подставив в (5) вместо число и решив систему (5), получим числа и . Затем положим в (5) и получим числа и, наконец, при получим и . Соответственно трем наборам чисел и получим три частных решения

Общее решение системы (3) имеет вид

Пример 1. Решить систему дифференциальных уравнений

Решение. Составляем характеристическое уравнение

Корням соответствуют числа

Выписываем частные решения

Общее решение системы:

Б. Рассмотрим теперь случай, когда корни характеристического уравнения комплексные .

Пример 2. Решить систему линейных однородных дифференциальных уравнений

Решение. Выпишем систему для определения и

имеет корни . Подставляя в (8), получаем два уравнения для определения и

из которых одно является следствием другого (в силу того, что определитель системы (8) равен нулю).

Возьмем , тогда первое частное решение запишется так:

Аналогично, подставляя в (8) корень , найдем второе частное решение:

Перейдем к новой фундаментальной системе решений:

Пользуясь известной формулой Эйлера , из (9), (10) и (11) получаем

Общим решением системы (7) будет

Замечание. Найдя первое частное решение (9), можно было бы сразу написать общее решение системы (7), пользуясь формулами

где и обозначают соответственно действительную и мнимую части комплексного числа , т. е. если , то , .

В. Случай кратных корней.

Пример 3. Решить систему

Решение. Характеристическое уравнение

Решение следует искать в виде

Подставляя (13) в первое уравнение системы (12), получаем

Приравнивая коэффициенты при одинаковых степенях в левой и правой части (14), получаем:

Величины и остаются произвольными. Обозначая их соответственно через и , получаем общее решение системы (12):

Замечание. Легко проверить, что если (13) подставить во второе уравнение системы (12), то получим тот же результат (15). В самом деле, из равенства

получаем два соотношения для определения и через и

Пример 4. Решить задачу Коши для системы линейных дифференциальных уравнений

с начальными условиями .

Решение. Характеристическое уравнение

Корни уравнения (17): . Действительному корню отвечает решение

Подставляя (18) в систему (16) и сокращая на , получаем

откуда . Полагаем, например, , тогда и частное решение (18):

Комплексному корню отвечает решение

подставив которое в (16) и сокращая на , получим

откуда , так что, например, при имеем и частное решение

Корню соответствует решение, комплексно сопряженное решению (20), т.е.

Учитывая (19), (20), (21), получаем общее решение

Выделим, наконец, решение с начальными условиями . Из (22) при имеем

Воспользовавшись формулами Эйлера , окончательно получим