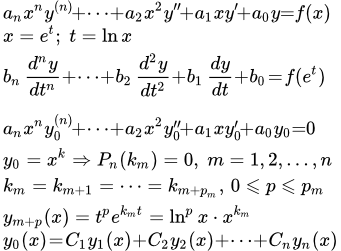Метод эйлера для уравнений 2 порядка

Метод эйлера для уравнений 2 порядка

Численное решение линейного однородного дифференциального уравнения 2 порядка методами Эйлера и Рунге-Кутта.

Рассматривается линейное однородное дифференциальное уравнение второго порядка вида

Для того, чтобы применить к нему численные методы Эйлера и Рунге-Кутта, следует свести это уравнение к системе 2-х дифференциальных уравнений 1-го порядка

Упростим : b=b/a, c=c/a.

Вводя новую функцию x(t), получаем :

К полученной системе применяем формулу Эйлера :

Затем применяется метод Рунге-Кутта. Расчет ведется по формулам :

В случае нашей системы формулы выглядят следующим образом :

Ниже приведен пример решения уравнения 3 y”+2y’+y=0 на отрезке t=[0..1] с шагом 0,01 в среде Maple ( текст программы)

Задаются коэффициенты дифференциального уравнения

Задание начальных условий

Задание правой границы отрезка

Уменьшение шага повысит точность вычислений

Расчет числа шагов

Вывод дифференциального уравнения

ur := a * diff ( y ( t ), t $2)+ b * diff ( y ( t ), t )+ c * y ( t )=0;

Вывод начальных условий

usl := y ( t 0)= y 0; usl 2:= D ( y )( t 0)= yy 0;

Перерасчет коэффициентов к виду y «+ by ‘+ cy =0

b := b / a : c := c / a :

Применяется метод Эйлера

print (`Метод Эйлера с шагом h `= h );

for i from 1 to n do

В цикле ведется расчет по формулам Эйлера

Если в следующей строке изменить «:» на «;» будут выводится результаты расчета на каждом шаге

Применяется метод Рунге-Кутта 3 порядка

print (`Метод Рунге-Кутта 3 порядка с шагом h `= h );

Метод эйлера для уравнений 2 порядка

Variant 19 (Sukach Maxim, BS17-03)

Найдем

В итоге, наше решение принимает вид:

Метод Эйлера дает возможность приближенно выразить функцию теоретически с любой наперед заданной точностью. Суть метода Эйлера в пошаговом вычислении значений решения y=y(x) дифференциального уравнения вида y’=f(x,y) с начальным условием (x0;y0). Метод Эйлера является методом 1-го порядка точности и называется методом ломаных.

Для вычисления используются следующие формулы:

Метод Эйлера и точное решение при x0 = 0, xf = 9, y0 = 1, h = 0.1

Метод Эйлера и точное решение при x0 = 0, xf = 3, y0 = 1, h = 0.1

Метод Эйлера и точное решение при x0 = 0, xf = 1, y0 = 1, h = 0.1

Усовершенствованный метод Эйлера

Суть усовершенствованного метода Эйлера в пошаговом вычислении значений решения y=y(x) дифференциального уравнения вида y’=f(x,y) с начальным условием (x0;y0). Усовершенствованный метод Эйлера является методом 2-го порядка точности и называется модифицированным методом Эйлера.

Разница между данным методом и методом Эйлера минимальна и заключается в использовании следующих формул:

Усовершенствованный Метод Эйлера и точное решение при
x0 = 0, xf = 9, y0 = 1, h = 0.1

Усовершенствованный Метод Эйлера и точное решение при
x0 = 0, xf = 3, y0 = 1, h = 0.1

Усовершенствованный Метод Эйлера и точное решение при
x0 = 0, xf = 1, y0 = 1, h = 0.1

Классический метод Рунге-Кутты

Суть метода Рунге-Кутты в пошаговом вычислении значений решения y=y(x) дифференциального уравнения вида y’=f(x,y) с начальным условием (x0;y0). Классический метод Рунге-Кутты является методом 4-го порядка точности и называется методом Рунге-Кутты 4-го порядка точности.

Ну и как обычно, формулы:

Классический метод Рунге-Кутты и точное решение при x0 = 0, xf = 9, y0 = 1, h = 0.1

Классический метод Рунге-Кутты и точное решение при x0 = 0, xf = 3, y0 = 1, h = 0.1

Классический метод Рунге-Кутты и точное решение при x0 = 0, xf = 1, y0 = 1, h = 0.1

Сравнение методов для заданной задачи

Размер ошибки всех методов на промежутке [0, 9] с шагом 0.1

Размер ошибки всех методов на промежутке [0, 3] с шагом 0.1

Размер ошибки всех методов на промежутке [0, 1] с шагом 0.1

Очевидно что, классический метод Рунге-Кутты справляется с задачей аппроксимации в случае данного уравнения намного лучше чем Метод Эйлера и Усовершенствованный метод Эйлера.

График глобальной средней ошибки

Глобальная ошибка в зависимости от размера шага H на промежутке от 0.01 до 0.91 для x0 = 1, xf = 9

Дифференциальное уравнение Эйлера и методы его решения

Более общее уравнение Эйлера имеет вид:
.
Это уравнение подстановкой t = ax+b приводится к более простому виду, которое мы и будем рассматривать.

Приведение дифференциального уравнения Эйлера к уравнению с постоянными коэффициентами.

Рассмотрим уравнение Эйлера:
(1) .
Оно сводится к линейному уравнению с постоянными коэффициентами подстановкой:
x = e t .
Действительно, тогда
;
;
;

;
;
.

Таким образом, множители, содержащие x m , сокращаются. Остаются члены с постоянными коэффициентами. Однако на практике, для решения уравнений Эйлера, можно применять методы решения линейных ДУ с постоянными коэффициентами без использования указанной выше подстановки.

Решение однородного уравнения Эйлера

Рассмотрим однородное уравнение Эйлера:
(2) .
Ищем решение уравнения (2) в виде
.
;
;
.
.
Подставляем в (2) и сокращаем на x k . Получаем характеристическое уравнение:
.
Решаем его и получаем n корней, которые могут быть комплексными.

Рассмотрим действительные корни. Пусть k_i – кратный корень кратности m . Этим m корням соответствуют m линейно независимых решений:
.

Рассмотрим комплексные корни. Они появляются парами вместе с комплексно сопряженными. Пусть k_i – кратный корень кратности m . Выразим комплексный корень k_i через действительную и мнимую части:
.
Этим m корням и m комплексно сопряженным корням соответствуют 2 m линейно независимых решений:
;
;
.
.

После того как получены n линейно независимых решений, получаем общее решение уравнения (2):
(3) .

Примеры

Решение неоднородного уравнения Эйлера

Рассмотрим неоднородное уравнение Эйлера:
.
Метод вариации постоянных (метод Лагранжа) также применим и к уравнениям Эйлера.

Сначала мы решаем однородное уравнение (2) и получаем его общее решение (3). Затем считаем постоянные функциями от переменной x . Дифференцируем (3) n – 1 раз. Получаем выражения для n – 1 производных y по x . При каждом дифференцировании члены, содержащие производные приравниваем к нулю. Так получаем n – 1 уравнений, связывающих производные . Далее находим n -ю производную y . Подставляем полученные производные в (1) и получаем n -е уравнение, связывающее производные . Из этих уравнений определяем . После чего интегрируя, получаем общее решение уравнения (1).

Пример

Неоднородное уравнение Эйлера со специальной неоднородной частью

Рассмотрим уравнение Эйлера со специальной неоднородной частью:
(4)
,
где – многочлены от степеней и , соответственно.

Наиболее простой способ решения такого уравнения заключается в том, чтобы сделать подстановку
,
и решать линейное уравнение с постоянными коэффициентами со специальной неоднородной частью.

Автор: Олег Одинцов . Опубликовано: 14-08-2013 Изменено: 24-10-2020