Метод эйлера с уточнением для решения дифференциальных уравнений

Метод Эйлера с уточнением

Дата добавления: 2013-12-23 ; просмотров: 4250 ; Нарушение авторских прав

Задача Коши

Дифференциальных уравнений

Численные методы решения обыкновенных

Раздел № 7

связывающее неизвестную функцию у(х),независимую переменную х и производные у’(x), у»(x). у ( n ) (x) неиз­вестной функции, называется обыкновенным дифферен­циальным уравнением. Порядок п старшей производной называется порядком дифференциального уравнения.

В задаче Коши для дифференциального уравнения п-го порядкаискомая функция у(х),кроме самого дифферен­циального уравнения, должна удовлетворять начальным условиям

Методы решения задач для дифференциальных урав­нений можно разбить на три типа: точные, приближен­ные и численные.

Точныминазывают методы, с помощью которых реше­ние дифференциального уравнения можно выразить че­рез известные функции (элементарные функции или ин­тегралы от элементарных функций). Точные методы решения известны только для некоторых классов диффе­ренциальных уравнений (линейные дифференциальные уравнения, уравнения с разделяющимися переменными и др.).

Приближенными называют методы, в которых реше­ние находят как предел последовательности функций, яв­ляющихся элементарными или интегралами от элементар­ных функций. Например, метод разложения искомой функции в ряд Тейлора является приближенным методом.

Численный метод решения дифференциального урав­нения – алгоритм вычисления значений искомого реше­ния у(х) на некотором дискретном множестве значений аргумента х. При этом вычисляемые значения искомого решения у(х) являются приближенными, но могут быть и точными.

Рассмотрим задачу Коши для обыкновенного диффе­ренциального уравнения первого порядка

Требуется найти функцию у = у(х), которая удовлет­воряет уравнению (7.1) на интервале (х₀, X) и начально­му условию (7.2) в точке х₀.

Приведем без доказательства теорему существования и единственности решения задачи Коши.

Теорема 7.1. Пусть в области R<(x, у), |х — х₀| £ а, |у — у₀| £ b> функция f(x, у) непрерывна. Тогда на некото­ром отрезке |х — x₀| £ d существует решение уравнения (7.1), удовлетворяющее условию (7.2).

Если в области R функция f(x, у) удовлетворяет усло­вию Липшица

то указанное решение единственно.

Произведем разбиение отрезка [х₀, X] на п частей:

x_i = x₀ + ih, 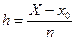. (7.3)

Найдем приближенные значения решения у(х) в точ­ках x_i , i = 1, 2. n.

7.2. Метод Эйлера (ломаных)

Рассмотрим уравнение (7.1) в точках x_i, i = 0, 1, . , n — 1 и заменим производную y‘(x_i) разностной формулой

y‘(x_i) = (7.4)

Тогда получим рекуррентную формулу метода Эйле­ра для вычисления приближенных значений у(x_{i + 1}):

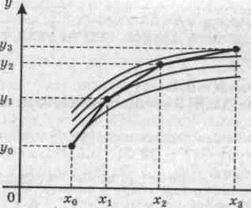
На рис. 7.1 дана геометрическая иллюстрация метода Эйлера (7.5). Уравнение касательной к графику решения у(х) в точке (х₀, у₀) имеет вид

удовлетворяющей уравнению (7.1) и начальному условию y(x₁) = y₁.

Таким образом, с каждым шагом i метод Эйлера (7.5) дает точки (x_i, y_i), которые, вообще говоря, удаляются от интегральной кривой, соответствующей точному решению задачи Коши (7.1), (7.2). Вместо интегральной кривой ме­тод Эйлера дает ломаную, изображенную на рис. 7.1, по­этому его часто называют методом ломаных.

Формулу (7.5) можно получить и другим способом. Рассмотрим разложение искомого решения у(х) в ряд Тейлора в окрестности точки х₀:

у(х) = у(х₀) + у ¢ (х₀)(х — х₀) + + . .

Также здесь получен следующий результат – погреш­ность вычисления значения у₁ есть величина порядка O(h 2 ), а погрешность значения у_п – величина порядка O(h). Из-за большой погрешности метод Эйлера применя­ется редко.

Для повышения точности метода Эйлера применяют следующий прием. Сначала находят приближенное зна­чение решения по методу Эйлера:

,

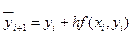
а затем уточняют его по формуле

.

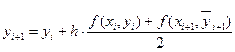
Этот метод называется методом Эйлера-Коши, и ре­куррентные соотношения для его реализации могут быть записаны в виде

, (7.7)

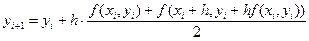
Метод Эйлера-Коши имеет погрешность порядка O(h 2 ). Геометрическая иллюстрация метода Эйлера-Коши пока­зана на рис. 7.2. Очередное приближение метода Эйлера-Коши соответствует точке пересечения диагоналей парал­лелограмма, построенного на двух звеньях ломаной метода Эйлера.

Метод Эйлера-Коши является одним из частных слу­чаев методов Рунге-Кутта.

Задачи с начальными условиями для систем обыкновенных дифференциальных уравнений

Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений $$ \begin \tag <1>\frac &= f_i (t, u_1, u_2, \ldots, u_n), \quad t > 0\\ \tag <2>u_i(0) &= u_i^0, \quad i = 1, 2, \ldots, m. \end $$

Используя векторные обозначения, задачу (1), (2) можно записать как задачу Коши $$ \begin \tag <3>\frac> &= \pmb(t, \pmb), \quad t > 0, \\ \tag <4>\pmb(0) &= \pmb_0 \end $$ В задаче Коши необходимо по известному решению в точке \( t = 0 \) необходимо найти из уравнения (3) решение при других \( t \).

Численные методы решения задачи Коши

Существует большое количество методов численного решения задачи (3), (4). Вначале рассмотрим простейший явный метод Эйлера и его программную реализацию. Затем будут представлены методы Рунге—Кутта и многошаговые методы.

При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.

Идея численных методов решения задачи (3), (4) состоит из четырех частей:

1. Вводится расчетная сетка по переменной \( t \) (время) из \( N_t + 1 \) точки \( t_0 \), \( t_1 \), \( \ldots \), \( t_ \). Нужно найти значения неизвестной функции \( \pmb \) в узлах сетки \( t_n \). Обозначим через \( \pmb^n \) приближенное значение \( \pmb(t_n) \).

2. Предполагаем, что дифференциальное уравнение выполнено в узлах сетки.

3. Аппроксимируем производные конечными разностями.

4. Формулируем алгоритм, который вычисляет новые значения \( \pmb^ \) на основе предыдущих вычисленных значений \( \pmb^k \), \( k 0 \) при \( \tau\to 0 \).

Явный метод Эйлера

Проиллюстрируем указанные шаги. Для начала введем расчетную сетку. Очень часто сетка является равномерной, т.е. имеет одинаковое расстояние между узлами \( t_n \) и \( t_ \): $$ \omega_\tau = \< t_n = n \tau, n = 0, 1, \ldots, N_t \>. $$

Затем, предполагаем, что уравнение выполнено в узлах сетки, т.е.: $$ \pmb^\prime (t_n) = \pmb(t_n, u(t_n)), \quad t_n \in \omega_\tau. $$

Заменяем производные конечными разностями. С этой целью, нам нужно знать конкретные формулы, как производные могут быть аппроксимированы конечными разностями. Простейший подход заключается в использовании определения производной: $$ \pmb^\prime(t) = \lim_ <\tau \to 0>\frac<\pmb(t+\tau) — \pmb(t)><\tau>. $$

В произвольном узле сетки \( t_n \) это определение можно переписать в виде: $$ \begin \pmb^\prime(t_n) = \lim_ <\tau \to 0>\frac<\pmb(t_n+\tau) — \pmb(t_n)><\tau>. \end $$ Вместо того, чтобы устремлять шаг сетки к нулю, мы можем использовать малый шаг \( \tau \), который даст численное приближение \( u^\prime(t_n) \): $$ \begin \pmb^\prime(t_n) \approx \frac<\pmb^ — \pmb^><\tau>. \end $$ Такая аппроксимация известна как разностная производная вперед и имеет первый порядок по \( \tau \), т.е. \( O(\tau) \). Теперь можно использовать аппроксимацию производной. Таким образом получим явный метод Эйлера: $$ \begin \tag <5>\frac<\pmb^ — \pmb^n> <\tau>= \pmb(t_n, \pmb^). \end $$

Четвертый шаг заключается в получении численного алгоритма. Из (5) следует, что мы должны знать значение \( y^n \) для того, чтобы решить уравнение (5) относительно \( y^ \) и получить формулу для нахождения приближенного значения искомой функции на следующем временном слое \( t_ \): $$ \begin \tag <6>\pmb^ = \pmb^n + \tau \pmb(t_n, \pmb^) \end $$

При условии, что у нас известно начальное значение \( \pmb^0 = \pmb_0 \), мы можем использовать (6) для нахождения решений на последующих временных слоях.

Программная реализация явного метода Эйлера

Выражение (6) может быть как скалярным так и векторным уравнением. И в скалярном и в векторном случае на языке Python его можно реализовать следующим образом

При решении системы (векторный случай), u[n] — одномерный массив numpy длины \( m+1 \) (\( m \) — размерность задачи), а функция F должна возвращать numpy -массив размерности \( m+1 \), t[n] — значение в момент времени \( t_n \).

Таким образом численное решение на отрезке \( [0, T] \) должно быть представлено двумерным массивом, инициализируемым нулями u = np.zeros((N_t+1, m+1)) . Первый индекс соответствует временному слою, а второй компоненте вектора решения на соответствующем временном слое. Использование только одного индекса, u[n] или, что то же самое, u[n, :] , соответствует всем компонентам вектора решения.

Функция euler решения системы уравнений реализована в файле euler.py:

Строка F_ = lambda . требует пояснений. Для пользователя, решающего систему ОДУ, удобно задавать функцию правой части в виде списка компонент. Можно, конечно, требовать чтобы пользователь возвращал из функции массив numpy , но очень легко осуществлять преобразование в самой функции решателе. Чтобы быть уверенным, что результат F будет нужным массивом, который можно использовать в векторных вычислениях, мы вводим новую функцию F_ , которая вызывает пользовательскую функцию F «прогоняет» результат через функцию assaray модуля numpy .

Неявный метод Эйлера

При построении неявного метода Эйлера значение функции \( F \) берется на новом временном слое, т.е. для решении задачи (5) используется следующий метод: $$ \begin \tag <7>\frac<\pmb^ — \pmb^n> <\tau>= \pmb(t_, \pmb^). \end $$

Таким образом для нахождения приближенного значения искомой функции на новом временном слое \( t_ \) нужно решить нелинейное уравнение относительно \( \pmb^ \): $$ \begin \tag <8>\pmb^ — \tau \pmb(t_, \pmb^) — y^n = 0. \end $$

Для решения уравнения (8) можно использовать, например, метод Ньютона.

Программная реализация неявного метода Эйлера

Функция backward_euler решения системы уравнений реализована в файле euler.py:

Отметим, что для нахождения значения u[n+1] используется функция fsolve модуля optimize библиотеки scipy . В качестве начального приближения для решения нелинейного уравнения используется значение искомой функции с предыдущего слоя u[n] .

Методы Рунге—Кутта

Одношаговый метод Рунге—Кутта в общем виде записывается следующим образом: $$ \begin \tag <9>\frac<\pmb^ — \pmb^n> <\tau>= \sum_^s b_i \pmb_i, \end $$ где $$ \begin \tag <10>\pmb_i = \pmb\left( t_n + c_i\tau, \pmb^n + \tau \sum_^s a_\pmb_j \right), \quad i = 1, 2, \ldots, s. \end $$ Формула (9) основана на \( s \) вычислениях функции \( \pmb \) и называется \( s \)-стадийной. Если \( a_ = 0 \) при \( j \geq i \) имеем явный метод Рунге—Кутта. Если \( a_ = 0 \) при \( j > i \) и \( a_ \ne 0 \), то \( \pmb_i \) определяется неявно из уравнения $$ \begin \tag <11>\pmb_i = \pmb\left( t_n + c_i\tau, \pmb^n + \tau \sum_^ a_\pmb_j + \tau a_ \pmb_i \right), \quad i = 1, 2, \ldots, s. \end $$ О таком методе Рунге—Кутта говорят как о диагонально-неявном.

Одним из наиболее распространенных является явный метод Рунге-Кутта четвертого порядка: $$ \begin \tag <12>\pmb_1 & = \pmb(t_n, \pmb^n), &\quad \pmb_2 &= \pmb\left( t_n + \frac<\tau><2>, \pmb^n + \tau \frac<\pmb_1> <2>\right),\\ \pmb_3 &= \pmb\left( t_n + \frac<\tau><2>, \pmb^n + \tau \frac<\pmb_2> <2>\right), &\quad \pmb_4 &= \pmb\left( t_n + \tau, \pmb^n + \tau \pmb_3 \right),\\ \frac<\pmb^ -\pmb^n> <\tau>&= \frac<1> <6>(\pmb_1 + 2\pmb_2 + 2\pmb_3 + \pmb_4) & & \end $$

Многошаговые методы

В методах Рунге—Кутта в вычислениях участвуют значения приближенного решения только в двух соседних узлах \( \pmb^n \) и \( \pmb^ \) — один шаг по переменной \( t \). Линейный \( m \)-шаговый разностный метод записывается в виде $$ \begin \tag <13>\frac<1> <\tau>\sum_^m a_i \pmb^ = \sum_^ b_i \pmb(t_, \pmb^), \quad n = m-1, m, \ldots \end $$ Вариант численного метода определяется заданием коэффициентов \( a_i \), \( b_i \), \( i = 0, 1, \ldots, m \), причем \( a_0 \ne 0 \). Для начала расчетов по рекуррентной формуле (13) необходимо задать \( m \) начальных значений \( \pmb^0 \), \( \pmb^1 \), \( \dots \), \( \pmb^ \) (например, можно использовать для их вычисления метод Эйлера).

Различные варианты многошаговых методов (методы Адамса) решения задачи с начальными условиями для систем обыкновенных дифференциальных уравнений могут быть получены на основе использования квадратурных формул для правой части равенства $$ \begin \tag <14>\pmb(t_) — \pmb(t_n) = \int_^> \pmb(t, \pmb) dt \end $$

Для получения неявного многошагового метода используем для подынтегральной функции интерполяционную формулу по значениям функции \( \pmb^ = \pmb(t_, \pmb^) \), \( \pmb^n \), \( \dots \), \( \pmb^ \), т.е. $$ \begin \tag <15>\frac<\pmb^ — \pmb^n> <\tau>= \sum_^ b_i \pmb(t_, \pmb^) \end $$

Для интерполяционного метода Адамса (15) наивысший порядок аппроксимации равен \( m+1 \).

Для построения явных многошаговых методов можно использовать процедуру экстраполяции подынтегральной функции в правой части (14). В этом случае приближение осуществляется по значениям \( \pmb^n \), \( \pmb^ \), \( \dots \), \( \pmb^ \) и поэтому $$ \begin \tag <16>\frac<\pmb^ — \pmb^n> <\tau>= \sum_^ b_i \pmb(t_, \pmb^) \end $$

Для экстраполяционного метода Адамса (16) погрешность аппроксимации имеет \( m \)-ый порядок.

На основе методов Адамса строятся и схемы предиктор–корректор. На этапе предиктор используется явный метод Адамса, на этапе корректора — аналог неявного метода Адамса. Например, при использовании методов третьего порядка аппроксимации в соответствии с (18) для предсказания решения положим $$ \frac<\pmb^ — \pmb^n> <\tau>= \frac<1> <12>(23 \pmb^ -16\pmb^ + 5\pmb^). $$ Для уточнеия решения (см. (17)) используется схема $$ \frac<\pmb^ — \pmb^n> <\tau>= \frac<1> <24>(9\pmb^ + 19\pmb^ — 5\pmb^ + \pmb^). $$ Аналогично строятся и другие классы многошаговых методов.

Жесткие системы ОДУ

При численном решении задачи Коши для систем обыкновенных дифференциальных уравнений (3), (4) могут возникнуть дополнительные трудности, порожденные жесткостью системы. Локальные особенности поведения решения в точке \( u = w \) передаются линейной системой $$ \begin \frac