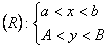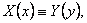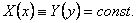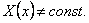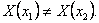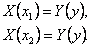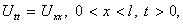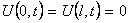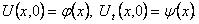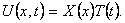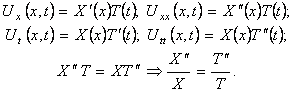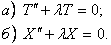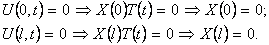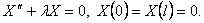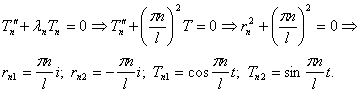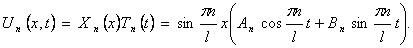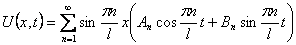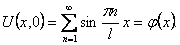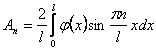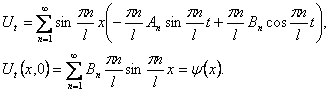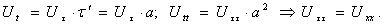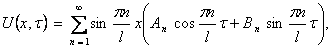1 Метод Фурье для неоднородного параболического уравнения с однородными краевыми условиями второго рода.
- Мария Огаркова 5 лет назад Просмотров:
1 1 Метод Фурье для неоднородного параболического уравнения с однородными краевыми условиями второго рода. 699 M. Решить неоднородную начально-краевую задачу для уравнения теплопроводности с однородными краевыми условиями второго рода. u t a u xx = fx, t, x,, t >, 1.1 u x, t = u x, t =, t >, 1. ux, = ϕx, x [, ]. 1.3 Шаг 1. Решение задачи Штурма Лиувилля. Рассмотрим задачу X x + λxx =, 1.4 X = X =. 1.5 Задача есть задача Штурма Лиувилля. Общее решение уравнения 1.4 имеет вид Xx = c 1 sin λ x + c cos λ x при λ > ; 1.6 Xx = c 1 e λ x + c e λ x при λ имеем из краевого условия X =, что c 1 =, Xx = c cos λ x X x = c λ sin λ x. Поэтому из второго краевого условия X = получаем, что λ = πk откуда имеем бесконечное множество собственных чисел задачи Штурма Лиувилля: πn λ n =, n N. 1.9 Им соответствует бесконечное множество собственных функций: X n x = cos, n N. 1.1 При λ 2 Шаг. Будем искать решение уравнения u t a u xx = fx, t с краевыми условиями u x, t = u x, t = в виде ux, t = X n T n t, где функции X n x имееют вид: n= X x 1, X n x = cos Заметим сразу, что каждое слагаемое приведённого ряда удовлетворяет краевым условиям 1., что достаточно если ряд допускает почленный переход к пределу при x +, x = для того, чтобы функция ux, t, определённая таким образом, также удовлетворяла краевым условиям 1.. Пусть функция fx, t разложена при каждом t [, T ] в ряд Фурье по косинусам fx, t = f t При этом, коэффициенты данного ряда Фурье ищутся по формулам: + cos f n t. 1.1 f n t = f, X n = fx, t cos dx Тогда уравнение 1.1 приобретает вид n= Xn xt nt a X n xt n t = f t Для его выполнения достаточно, чтобы + f n t cos. то есть T t = f t X n xt nt a X n xt n t = f n t cos T t = f t T nt + πna T n t cos = f n t cos для n = для n N, для n = для n N. Это заведомо выполнено, если T t = f t для n = 1.14 T nt + πna T n t = f n t для n N, 1.15 Итак, мы получили условия на функции T n t, достаточные для того, чтобы функция ux, t = T n t cos была если ряд «хороший» решением уравнения n= u t a u xx = fx, t с краевыми условиями u x, t = u x, t =. Шаг 3. Решаем задачу Из условий задачи мы ещё не использовали только начальные условия —
3 ux, = ϕx. Пусть функция ϕx, входящая в начальное условие, разлагается в ряд по косинусам Подставим функцию ux, t = T n t cos опять-таки в предположении, что ряд «хороший» в начальное условие: ϕx = ϕ + ϕ n cos, x [, ] где 1.16 n= n= ϕ n = ϕx cos dx T n cos = ϕ + ϕ n cos. Для выполнения этого равенства достаточно, чтобы T = ϕ для n = T n = ϕ n для n N. Таким образом, из 1.14, 1.15 и , для функций T n t имеем задачу Коши: T t = f t T = ϕ T nt + πna T n t = f n t для n = 1.18 T n = ϕ n для n N Эти задачи Коши имеют единственное решение при любых f n C[, T ] и любых значениях ϕ n R. При n = : T t = ϕ + 1 t f τdτ. 1. При n N: сначала решаем однородное уравнение: Его общее решение имеет вид: T nt + πna T n t =. T n t = c e πna t. Метод вариации постоянной позволяет нам искать решение уравнения 1.19 в виде T n t = cte πna t, = T nt = c t πna ct e πna t. Подставив эти равнества в 1.19, получим уравнение для нахождения ct: c t = f n te πna t, -3-
4 откуда, с учётом начального условия T n = ϕ n, ct = ϕ n + t f n τe πna τ dτ. 1.1 Таким образом, t T n t = ϕ n e πna t + f n τe πna t τ dτ. 1. Всё, что нам осталось сделать, это подставить 1., 1. в формулу Получаем ответ: ux, t = ϕ + 1 t f τdτ + ux, t = n= T n t cos. ϕ n e πna t + t f n τe πna t τ dτ cos 669 M. Решить неоднородную начально-краевую задачу для уравнения колебаний с однородными краевыми условиями второго рода.. u tt a u xx = fx, t, x,, t >,.1 u x, t = u x, t =, t >,. ux, = ϕx, x [, ]..3 u t x, = ψx, x [, ]..4 Шаг 1. Решение задачи Штурма Лиувилля. Этот шаг полностью повторяет Шаг 1. задачи 699 M. Шаг. Будем искать решение уравнения u tt a u xx = fx, t с краевыми условиями u x, t = u x, t = в виде ux, t = X n T n t, где функции X n x имееют вид: n= X x 1,.5 X n x = cos..6 Пусть функция fx, t разложена при каждом t [, T ] в ряд Фурье по косинусам fx, t = f t При этом, коэффициенты данного ряда Фурье ищутся по формулам: + cos f n t..7 f n t = f, X n = fx, t cos dx..8-4-
5 Тогда уравнение.1 приобретает вид n= Xn xt n t a X n xt n t = f t Для его выполнения достаточно, чтобы то есть T t = f t X n xt n t a X n xt n t = f n t cos + f n t cos. T t = f t T n t + πna T n t cos = f n t cos Это заведомо выполнено, если T t = f t для n = для n N, для n = для n N. для n =.9 T n t + πna T n t = f n t для n N,.1 Итак, мы получили условия на функции T n t, достаточные для того, чтобы функция ux, t = T n t cos была если ряд «хороший» решением уравнения n= u tt a u xx = fx, t с краевыми условиями u x, t = u x, t =. Шаг 3. Решаем задачу.1.4. Из условий задачи.1.4 мы ещё не использовали только начальные условия ux, = ϕx, u t x, = ψx. Пусть функции ϕx, ψx, входящие в начальные условия, разлагаются в ряд по косинусам Подставим функцию ux, t = T n t cos опять-таки в предположении, что ряд «хороший» в начальные условия: ϕx = ϕ + ϕ n cos, x [, ] где.11 ϕ n = ϕx cos dx..1 ψx = ψ + ψ n cos, x [, ] где.13 n= n= ψ n = ψx cos dx..14 T n cos = ϕ + ϕ n cos ; -5-
6 n= УМФ семинар Метод Фурье T n cos = ψ + ψ n cos. Для выполнения этих равенств достаточно, чтобы T = ϕ T = ψ для n = T n = ϕ n T n = ψ n для n N. Таким образом, из.9,.1 и.11.1, для функций T n t имеем задачу Коши: T t = f t T = ϕ для n =.15 T = ψ T n t + πna T n t = f n t T n = ϕ n для n N..16 T n = ψ n Эти задачи Коши имеют единственное решение при любых f n C[, T ] и любых значениях ϕ n R, ψ n R. При n = : T t = ϕ t + При n N: сначала решаем однородное уравнение: Его общее решение имеет вид: ψ + 1 τ T n t + πna T n t =. T n t = c 1 sin πnat f κdκ dτ c cos πnat. Метод вариации постоянной позволяет нам искать решение уравнения.16 в виде T n t = c 1 t sin πnat + c t cos πnat, где c 1, t есть решения системы c 1t sin πnat πna c 1 t cos πnat + c t cos πnat = ; c t sin πnat = fn t. откуда c 1t = πna f nt cos πnat, c t = πna f nt sin πnat. С учётом начальных условий T n = ϕ n, T n = ψ n окончательно получаем c 1 t = πna ψ n + t f n τ cos πnaτ dτ, c t = ϕ n t f n τ sin πnaτ dτ..18 πna πna -6-
7 Таким образом, T n t = ϕ n sin πnat + πna + ψ n πna sin πnat πnat cos + t f n τ cos πnaτ dτ cos πnat t f n τ sin πnaτ Всё, что нам осталось сделать, это подставить.17,.19 в формулу ux, t = T n t cos. n= dτ M. Классический способ. Решить неоднородную начально-краевую задачу для уравнения колебаний с однородными краевыми условиями второго рода. u tt a u xx = fx, x,, t >, 3.1 u, t = u, t =, t >, 3. ux, = β α x + α, x [, ]. 3.3 u t x, =, x [, ]. 3.4 Шаг 1. Решение задачи Штурма Лиувилля. Рассмотрим задачу 3.5 X x + λxx =, 3.6 X = X =. 3.7 Задача есть задача Штурма Лиувилля. Её решение нам уже известно: λ n =, X n x = sin, n N. Шаг. Будем искать решение уравнения u tt a u xx = fx, t с краевыми условиями u, t = u, t = в виде ux, t = X n T n t, где функции X n x имееют вид: X n x = sin, n N. 3.8 Пусть функция fx разложена в ряд Фурье по синусам так как в данном примере f не зависит от t, то f n тут просто константы, не зависящие от t fx = sin f n. 3.9 При этом, коэффициенты данного ряда Фурье ищутся по формулам: f n = f, X n = fx sin dx
8 Тогда уравнение 3.1 приобретает вид Xn xt n t a X n xt n t = Для его выполнения достаточно, чтобы X n xt n t a X n xt n t = f n sin то есть T n t + πna T n t sin = f n sin Это заведомо выполнено, если f n sin. для n N, для n N. T n t + πna T n t = f n для n N, 3.11 Итак, мы получили условия на функции T n t, достаточные для того, чтобы функция ux, t = T n t sin была если ряд «хороший» решением уравнения n= u tt a u xx = fx, t с краевыми условиями u, t = u, t =. Шаг 3. Решаем задачу Из условий задачи мы ещё не использовали только начальные условия ux, = ϕx = α β x α, u t x, = ψ =. Найдём разложение функций ϕx, ψx, входящих в начальные условия, в ряд по синусам ϕx = ψx = Подставим функцию ux, t = ϕ n sin, где ϕ n = ϕx sin ψ n sin, где ψ n = ψx sin T n t sin опять-таки в предположении, что ряд «хороший» в начальные условия: T n sin = dx. 3.1 dx T n sin = Для выполнения этих равенств достаточно, чтобы ϕ n sin ; ψ n sin. T n = ϕ n T n = ψ n для n N. Таким образом, из 3.11 и , для функций T n t имеем задачу Коши: T n t + πna T n t = f n T n = ϕ n для n N T n = ψ n -8-
9 Эти задачи Коши имеют единственное решение при любых f n R и любых значениях ϕ n R, ψ n R. Найдём ϕ n, ψ n из 3.1, 3.13 с учётом, что ϕx = β α x + α, ψ =. ϕ n = ϕx sin dx = + α β cos πn πn > << >β α x cos dx + α x= + x= sin dx = = 1n β α + α 1 1n = πn πn πn α 1n β, ψ n =. При n N: сначала решаем однородное уравнение: Его общее решение имеет вид: T n t + πna T n t =. T n t = c 1 sin πnat + c cos πnat. Простой вид правой части позволяет нам угадать частное решение неоднородного уравнения 3.14 в виде константы: f n. Поэтому общее решение 3.14 имеет вид: πna T n t = c 1 sin πnat + c cos πnat Из начального условия T n = ψ n = следует, что c 1 =. + f n πna. А второе начальное условие T n = ϕ n = πn α 1n β даёт нам c = πn α 1n β f n πna. Таким образом, T n t = πn α 1n β f n cos πnat + f n πna πna
10 Всё, что нам осталось сделать, это подставить 3.15 в формулу Получим ответ: ux, t = ux, t = T n t sin. πn α 1n β f n cos πnat sin + πna f n πna sin. 654 M. Короткий способ. Решить неоднородную начально-краевую задачу для уравнения колебаний с однородными краевыми условиями второго рода. u tt a u xx = fx, x,, t >, 4.1 u, t = u, t =, t >, 4. ux, = β α x + α, x [, ]. 4.3 u t x, =, x [, ]. 4.4 Шаг 1. Так как правые части всех равенств в этой задаче не зависят от времени, будем искать решение задачи в виде суммы ux, t = vx, t + wx. Найдём w = wx такую, чтобы 4.5 w tt a w xx = fx, x,, t >, 4.6 w, t = w, t =, t >. 4.7 Раз w = wx, то w tt =, и задача принимает более простой вид: Проинтегрируем уравнение 4.8 один раз: Проинтегрируем второй раз: w x = fx, a x,, 4.8 w = w =. 4.9 w x = 1 a wx = 1 a x y x fsds + c 1. fsdsdy + c 1 x + c. Из краевого условия w = получаем, что c =, а из w =, что = 1 a y fsdsdy + c 1, -1-
11 откуда c 1 = 1 a Итак, функция wx нам полностью известна: wx = x a y y fsdsdy. fsdsdy 1 a Тогда для vx, t = ux, t wx получается задача x y fsdsdy. 4.1 v tt a v xx =, x,, t >, 4.11 v, t = v, t =, t >, 4.1 vx, = β α x + α wx = ϕx, x [, ] v t x, =, x [, ] Такую задачу мы уже умеем решать см. номер 643. Её ответ: vx, t = sin A n cos где A n и B n задаются равенствами πna t + B n sin πna 4.15 t, 4.16 A n = ϕx sin dx; 4.17 B n = ψx sin aπn В нашем случае ψ =, а ϕ = β α x + α wx, откуда A n = β α x + α wx sin dx dx, B n = и функция v имеет вид vx, t = A n sin cos πnat Всё, что нам осталось сделать, это подставить в формулу найденные функции v и wиз 4.19 и 4.1. ux, t = vx, t + wx -11-
12 667. Решить неоднородную начально-краевую задачу для уравнения колебаний с однородными краевыми условиями второго рода. u tt a u xx = fx, t, x,, t >, 5.1 u, t = u x, t =, t >, 5. ux, =, x [, ]. 5.3 u t x, =, x [, ]. 5.4 Шаг 1. Решение задачи Штурма Лиувилля. Этот шаг мы проходили, когда решали задачу 649 M. Результат: бесконечное множество нетривиальных решений πn 1 πn 1x λ n =, X n x = sin, n N. Шаг. Будем искать решение уравнения u tt a u xx = fx, t с краевыми условиями u x, t = u x, t = в виде ux, t = X n T n t, где функции X n x имееют вид: n= 5.5 πn 1x X n x = sin. 5.6 Пусть функция fx, t разложена при каждом t [, T ] в ряд Фурье по функциям X n x: πn 1x fx, t = sin f n t. 5.7 При этом, коэффициенты данного ряда Фурье ищутся по формулам как мы убедились, решая 649 M : f n t = f, X n = πn 1x fx, t sin dx. 5.8 Тогда уравнение 5.1 приобретает вид Xn xt n t a X n xt n t = n= Для его выполнения достаточно, чтобы πn 1x X n xt n t a X n xt n t = f n t sin πn 1x f n t sin. то есть T n t + π n 1 a πn 1x πn 1x T 4 n t sin = f n t sin Это заведомо выполнено, если для n N, для n N. T n t + π n 1 a 4 T n t = f n t для n N,
13 Итак, мы получили условия на функции T n t, достаточные для того, чтобы функция ux, t = T n t cos была если ряд «хороший» решением уравнения n= u tt a u xx = fx, t с краевыми условиями u x, t = u x, t =. Шаг 3. Решаем задачу Из условий задачи мы ещё не использовали только начальные условия ux, =, u t x, =. Функции ϕx, ψx, входящие в начальные условия, разлагаются в ряд по функциям X n x πn 1x ϕx = ϕ n sin ψx = ψ + ψ n cos Подставим функцию ux, t = T n t sin «хороший» в начальные условия: πn 1x πn 1x T n sin = πn 1x T n sin =, x [, ] где ϕ n =, 5.1, x [, ] где ψ n = 5.11 опять-таки в предположении, что ряд πn 1x ϕ n sin = ; πn 1x ψ n sin =. Для выполнения этих равенств достаточно, чтобы T n = ϕ n = T n = ψ n = для n N. Таким образом, из 5.9 и , для функций T n t имеем задачу Коши: T n t + π n 1 a T 4 n t = f n t T n = n N. 5.1 T n = Эти задачи Коши имеют единственное решение при любых f n C[, T ] и любых значениях ϕ n R, ψ n R. сначала решаем однородное уравнение: Его общее решение имеет вид: T n t = c 1 sin T n t + π n 1 a 4 T n t =. πn 1at + c cos πn 1at. Метод вариации постоянной позволяет нам искать решение уравнения 5.1 в виде T n t = c 1 t sin πn 1at + c t cos πn 1at, где c 1, t есть решения системы -13-
14 откуда c 1t sin πn 1at πn 1a + c t cos πn 1at = ; c 1t cos πn 1at c t sin πn 1at = f n t. c 1t = πn 1a f nt cos πn 1at, c t = πn 1a f nt sin πn 1at. С учётом начальных условий T n = ϕ n =, T n = ψ n = окончательно получаем c 1 t = t πn 1aτ f n τ cos dτ, πn 1a Таким образом, T n t = c t = πn 1at t πn 1aτ sin f n τ cos dτ πn 1a cos πn 1at t πn 1aτ f n τ sin dτ. πn 1a 5.13 t f n τ sin Всё, что нам осталось сделать, это подставить 5.14 в формулу I. Найти решение ux, t задачи ux, t = T n t sin πn 1x. πn 1aτ dτ u tt a u xx = fx, t, x,, t >, 5.15 u, t = u, t =, t >, 5.16 ux, = ϕx, x [, ] u t x, =, x [, ] Решение: см. 654 M Классический способ, стр II. Найти решение ux, t задачи u t a u xx = fx, x,, t >, 5. u, t = u, t =, t >, 5.1 ux, = ϕx, x [, ]. 5. Решение: см. 654 M Короткий способ, стр
Лекция 3. Метод Фурье
Метод Фурье — один из распространенных и эффективных методов решения уравнений с частными производными. Этот метод часто встречается и под другими названиями: метод разделения переменных или метод собственных функций.
Общая схема метода Фурье.
Основная идея этого метода состоит в том, что решение задачи для уравнения с частными производными сводится к решению вспомогательных задач для уравнений с меньшим числом независимых переменных. В частности, если заданное уравнение содержит две независимые переменные, то вспомогательные задачи будут уже зависеть только от одной переменной. Таким образом решение уравнения с частными производными сводится к решению обыкновенных дифференциальных уравнений.
При применении метода Фурье удобно использовать следующую лемму.
Основная лемма метода Фурье.
Если в прямоугольнике R плоскости XOY:
для некоторых функций выполняется тождество
то в этом случае
Доказательство. Предположим противное, т.е. что
Тогда существуют значения 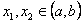
Рассмотрим точки (x1,y) и (x2,y), принадлежащие прямоугольнику R. На R справедливо тождество (8), а поэтому
Сравнивая эти равенства, приходим к противоречию с нашим предположением. Следовательно X(x) = const, а тогда Y(y)=const.
Решение первой начально-краевой задачи для волнового уравнения.
Рассмотрим волновое уравнение
Граничные условия первого рода
И начальные условия
Решим эту задачу методом Фурье.
Шаг 1. Представим функцию U(x,t) в виде
Найдем частные производные Uxx и Utt и подставим в уравнение (9):
В полученном уравнении левая часть зависит только от x, а правая- только от t. Используя основную лемму, заключаем:
Из граничных условий (10) получим
Шаг 2. Решим задачу Штурма-Лиувилля
Она имеет собственные значения и собственные функции
Шаг 3. Подставим найденные значения λn в уравнение а) и решим его:
Шаг 4. Выпишем частные решения уравнения (9):
Для волнового уравнения эти решения называются собственными колебаниями. В лекции 6 мы изучим их подробнее. В силу линейности и однородности уравнения (9) линейная комбинация этих решений
Замечание 1. Здесь мы предполагаем, что полученный функциональный ряд равномерно сходится и его можно дважды почленно дифференцировать по x и по t в области 0 0. Об условиях, при которых это можно сделать, будет рассказано в лекции 5.
Шаг 5. Определим коэффициенты Anи Bn в формуле (12), используя начальные условия (11). Из первого начального условия получим
Равенство (13) означает, что начальная функция φ(x) разлагается в ряд Фурье по синусам, которые в данном случае являются собственными функциями Xn(x) задачи Штурма-Лиувилля.
Коэффициенты Фурье вычисляются по формулам
Из второго начального условия находятся коэффициенты Bn.
Вычислив коэффициенты An и Bn для конкретных начальных функций и подставив их значения в (12), мы получим решение первой начально-краевой задачи.
Замечание 2. Используя формулу (12), можно получить решение первой начально-краевой задачи для уравнения колебания струны: Для этого проведем замену переменной τ=at и получим
При этом начальное условие не изменится, а условие преобразуется к виду Тогда решение задачи в переменных (x,τ) будет иметь вид
Возвращаясь к переменным (x,t), получим
http://vicaref.narod.ru/PDE/index3.htm