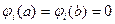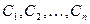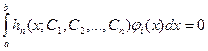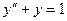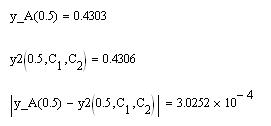Метод галеркина для уравнения пуассона

Метод галеркина для решения краевых задач

Метод Галеркина используется для приближенного решения краевых задач для дифференциальных уравнений, как обыкновенных, так и в частных производных.

Рассмотрим краевую задачу

(3.1)

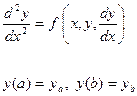
Для ее приближенного решения выберем какую-либо последовательность базисных функций

(3.2)

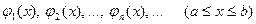
т. е. последовательность функций, удовлетворяющих соответствующим однородным краевым условиям

и обладающих свойством полноты. Последнее означает, что любую функцию из достаточно широкого класса, удовлетворяющую указанным однородным краевым условиям, можно разложить в ряд по функциям (3.2).

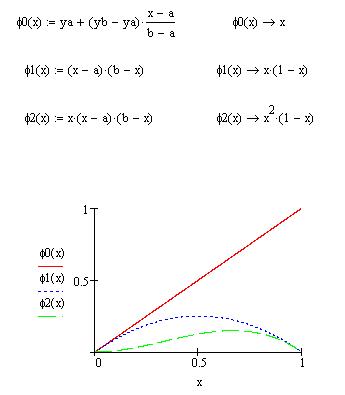
Чаще всего полагают

или , .

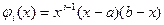
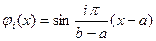
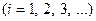
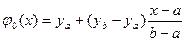
Кроме того, надо выбрать какую-нибудь функцию , удовлетворяющую краевым условиям, указанным в (3.1), например,

или

Приближенное решение задачи (3.1) ищется в виде

, (3.3)

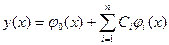
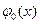
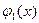
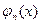
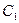
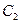
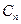
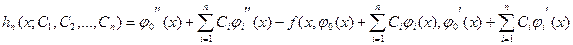
где функции , , … мы задаем, а постоянные , , … , подбираем. Тогда краевые условия, указанные в (3.1), заведомо удовлетворяются, а при подстановке выражения (3.3) в дифференциальное уравнение получается невязка (т. е. разность между левой и правой частями уравнения)

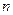
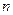
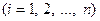
С ее помощью получаем систему из уравнений с неизвестными для определения

3.2. Реализация метода Галеркина в|посредством| MathCad

Пример. Найти методом Галеркина приближенное решение краевой задачи

, .

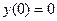
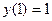
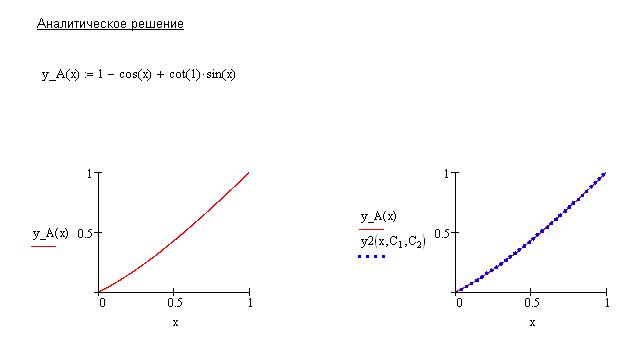
Приведем решение краевой задачи с помощью|посредством| программного комплекса MathCad:

Сравним, значения точного и приближенного решений:

например, при 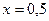имеем

Как видим, погрешность близка к 0,03 %. Для получения более точного решения необходимо использовать большее количество базисных функций.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Увлечёшься девушкой-вырастут хвосты, займёшься учебой-вырастут рога 9966 — | 7768 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Будем искать приближенное решение этой краевой задачи в виде суммы

Пусть дано дифференциальное уравнение с линейными краевыми условиями

где % Читайте также: Как настроить микрофон для караоке на ноутбуке

x ), которая на [а, Ь] будет сколь угодно точно приближать функцию у(х) вместе с ее производными У(х) и у»(х).

Докажем, что если для некоторой функции F(x) и полной системы функций

причем с_кк 5*0, иначе (р_к . Здесь оператор L [ ⋅ ] может содержать частные или полные производные искомой функции.

Содержание

Основа метода [ править | править код ]

Первым шагом в реализации метода Галёркина является выбор набора базисных функций, которые:

удовлетворяют граничным условиям.
в пределе бесконечного количества элементов базиса образуют полную систему.

Конкретный вид функций определяется из специфики задачи и удобства работы. Часто применяются тригонометрические функции, ортогональные полиномы (полиномы Лежандра, Чебышёва, Эрмита и др.).

Решение представляется в виде разложения по базису:

ψ ( x ) = ∑ k = 1 n α k ϕ k ( x ) . alpha _ phi _ (x).>

Затем приближённое решение подставляется в исходное дифференциальное уравнение, и вычисляется его невязка. Для однородного уравнения:

L [ ∑ k = 1 n α k ϕ k ( x ) ] = N ( x ) . alpha _ phi _ (x)
ight]=N(x).>

Для неоднородного уравнения L [ u ] = f ( x ) невязка будет иметь вид N ( x ) = L [ u ] − f ( x ) .

Далее выдвигается требование ортогональности невязки к базисным функциям, то есть:

∫ a b N ( x ) ϕ k ( x ) ρ ( x ) d x = 0. (x)
ho (x)dx>=0.>

Отсюда получается однородная система уравнений для коэффициентов в разложении, и удаётся приближённо найти собственные значения задачи.

Пример [ править | править код ]

ψ ″ + λ ψ = 0 ,

с граничными условиями:

ψ ( 0 ) = ψ ( 1 ) = 0.

Решение данного уравнения известно:

ψ ( x ) = sin ⁡ π n x , λ = π 2 n 2 , n = 1 , 2.. n^ ,qquad n=1,2..>

Для первого нетривиального решения ( n = 1 ) собственное число равно λ = π 2 ≈ 9 , 869. approx 9,869. > .

Теперь применим метод Галёркина. Выберем сперва одну базисную функцию:

ϕ 0 ( x ) = x ( 1 − x ) , ψ ( x ) = a 0 ϕ 0 ( x ) . (x)=x(1-x),qquad psi (x)=a_ phi _ (x).>

Подставляя в уравнение, получим невязку:

N ( x ) = a ( ϕ ″ + λ ϕ ) ,

и требование ортогональности невязки перепишется в виде:

∫ 0 1 ϕ ″ ϕ d x + λ ∫ 0 1 ϕ 2 d x = 0. ^

+lambda int limits _ ^

dx>=0.>

λ = − ∫ 0 1 ϕ ″ ϕ d x ∫ 0 1 ϕ 2 d x = ∫ 0 1 ( ϕ ′ ) 2 d x ∫ 0 1 ϕ 2 d x . ^

over int limits _ ^

dx>>= ^ dx> over int limits _ ^

dx>>.>

В приводимом здесь примере получается λ = 10 , что менее чем на 1,5 % отличается от точного решения. Задание большего числа базисных функций позволяет уточнить уже известное значение λ, а также получить первое приближение для следующего (соответствующего n=2).

Представим решение в виде линейной комбинации n функций:

ψ ( x ) = ∑ k = 1 n α k ϕ k ( x ) . alpha _ phi _ (x).>

N = ∑ k = 1 n N k ( x ) N_ (x)> .

Система уравнений для коэффициентов разложения:

∑ k = 1 n α k ∫ a b ϕ j N k d x = 0 , j = 1.. n . alpha _ int limits _^

N_ dx>=0,quad j=1..n.>

В этом случае собственные значения находятся из условия разрешимости системы (равенство нулю её определителя):

det ⁡ ( A j k ) = 0 , A j k = ∫ a b ϕ j N k d x left(A_
ight)=0,quad A_ =int limits _^

N_ dx>>

Важно помнить, что сходимость метода Галёркина не всегда быстро достигается. Успешное применение возможно только для т. н. самосопряжённых задач, то есть инвариантных к эрмитовому сопряжению.

Разновидности [ править | править код ]

Метод Галёркина имеет несколько усовершенствованных вариантов:

Метод Галёркина — Петрова — разложение решения производится по одному базису, а ортогональность невязки требуется к другому.
Метод Галёркина — Канторовича — позволяет свести уравнения в частных производных к обыкновенным дифференциальным уравнениям. Например, в двумерной задаче решение представляется в виде: ψ ( x , y ) = ∑ n b n X n ( x ) Y n ( y ) , b_ X_ (x)Y_ (y),>и процедура Галёркина проводится применительно лишь к одним функциям (здесь X n ( x ) (x)>либо Y n ( y ) (y)>). В итоге получается система ОДУ, для решения которых существуют эффективные численные методы. Данный приём подобен известному в квантовой механике методу Хартри — Фока.

Применение [ править | править код ]

Методы Галёркина давно применяются как для решения дифференциальных уравнений с частными производными, так и для формирования основы метода конечных элементов.

Применение метода к исследованию задач устойчивости гидродинамических течений было реализовано Г. И. Петровым, который доказал сходимость метода Галёркина для отыскания собственных значений широкого класса уравнений, включая уравнения для неконсервативных систем, такие, как например уравнения колебаний в вязкой жидкости.

В гидродинамике наиболее эффективно метод Галёркина работает в задачах о конвекции, в силу их самосопряжённости. Задачи о течениях таковыми не являются, и сходимость метода при неудачном выборе базиса может быть сильно затруднена.

Происхождение названия [ править | править код ]

Метод приобрёл популярность после исследований Бориса Галёркина (1915). Однако этот метод разработал не он, а Вальтер Ритц (1908), на которого Галёркин ссылается в своих первых публикациях. Его также применял Иван Бубнов (1913) для решения задач теории упругости. Поэтому иногда этот метод называют методом Бубнова — Галёркина. Теоретически метод был обоснован советским математиком Мстиславом Келдышем в 1942.

Численная аппроксимация линий тока методом Галёркина Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Панкратов И.А.

В статье рассмотрена задача о циркуляции воды в озере под действием ветра. Задача сведена к уравнению Пуассона относительно функции тока, которое было решено методом Галёркина с одновременной аппроксимацией краевых условий и методом частичной дискретизации. Приведены примеры численного решения. Работа является развитием 2.

NUMERICAL STREAMLINE’S APPROXIMATION BY GALERKIN METHOD

In this article we consider the problem of the water circulation in the lake caused by the wind. The problem was reduced to the Poisson equation for the stream function. It was solved by Galerkin method and partial discretization method. Examples of numerical solution are given. In this article we develop the results obtained in 1.

Текст научной работы на тему «Численная аппроксимация линий тока методом Галёркина»

ЧИСЛЕННАЯ АППРОКСИМАЦИЯ ЛИНИЙ ТОКА МЕТОДОМ ГАЛЁРКИНА

Саратовский национальный исследовательский государственный университет имени Н. Г. Чернышевского Россия, 410012, г. Саратов, ул. Астраханская, 83 * email: PankratovIA@info.sgu.ru

Ключевые слова: метод Галёркина, линия тока, ветровая нагрузка.

NUMERICAL STREAMLINE’S APPROXIMATION BY GALERKIN METHOD I. A. Pankratov*

National Research Saratov State University 83 Astrakhanskaya St., 410012, Saratov, Russia * email: PankratovIA@info.sgu.ru

Keywords: Galerkin method, streamline, wind stress.

Для расчёта течений в озерах, бассейнах и других водоёмах при-меняется упрощенная модель с целью начальной оценки циркуляции, которая затем может быть сопоставлена с результатами применения полных уравнений количества движения в мелководных бассейнах [4]. Линеаризованные уравнения таких течений получаются из уравнений количества движения, если отбросить инерционные члены, т.е.

и рассмотреть стационарное уравнение неразрывности:

Здесь f — параметр Кориолиса; дх и — компоненты средних значений массового расхода; р — плотность жидкости; Н — расстояние от оси х до дна, а п Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Вычисляя интегралы, входящие в (12), с учётом ортогональности системы базисных функций на отрезке [0;1], имеем следующую систему обыкновенных дифференциальных уравнений (т = 1М):

Граничные условия для системы (13) имеют вид

При этом граничные условия типа Дирихле удовлетворяются за счёт первого слагаемого в Щ.

Общее решение указанной системы, найденное методом Эйлера [7], есть

Произвольные постоянные интегрирования ст и сгт легко находятся из условий (14). Очевидно, что если т — чётное число, то ст=ст=о

Результаты решения задачи о циркуляции воды в озере с учётом потока от втекающей в него реки приведены на рис. 3,4. Показаны линии тока для щ = 0.1, щ = 0.3. щ = 0.9, (снизу вверх).

Рис. 3. Циркуляция воды в озере, M = 3, A = 0

0 0.2 0.4 0.6 0.8 1

Рис. 4. Циркуляция воды в озере, M = 3, A = 2

4. Коннор Дж., Бреббиа К. Метод конечных элементов в механике жидкости. Л.: Судостроение, 1979. 264 с.

5. Зенкевич О., Морган К. Конечные элементы и аппроксимация. М.: Мир, 1986. 318 с.

6. Алексеев Е. Р., Чеснокова О. В., Рудченко Е. А. Scilab: Решение инженерных и математических задач. М.: ALT Linux; БИНОМ. Лаборатория знаний, 2008. 269 с.

7. Понтрягин Л. С. Обыкновенные дифференциальные уравнения. М.: Наука, 1974. 331 с.

Поступила в редакцию 29.02.2016

Отметим, что в отличие от способа, рассмотренного в предыдущем параграфе, при применении метода частичной дискретизации приближённое решение задачи задаётся аналитическими формулами и не требуется численно решать систему алгебраических уравнений. В ходе численного решения задачи было установлено, что при увеличении количества базисных функций произвольные постоянные ст и ст , а также последнее слагаемое в (15) быстро стремятся к нулю. При этом братьМ> 5 нецелесообразно, так как в этом случае приближённое решение уже практически не изменяется.

В дальнейшем предполагается применить рассмотренный выше метод в случае, когда внутри озера находится остров в форме прямоугольника или эллипса.

1. Маркелова О.И., Панкратов И.А. Расчет циркуляции воды в озере // Математика. Механика. 2014. № 16. С. 114-117.

2. Панкратов И.А., Рымчук Д.С. Расчёт течений мелкой воды // Математика. Механика. 2014. № 16. С. 120-124.

3. Ильясова Т.А., Панкратов И.А. Математическое моделирование циркуляции воды в озере // Математика. Механика. 2015. № 17. С. 101-104.

источники:

http://cyberleninka.ru/article/n/chislennaya-approksimatsiya-liniy-toka-metodom-galyorkina