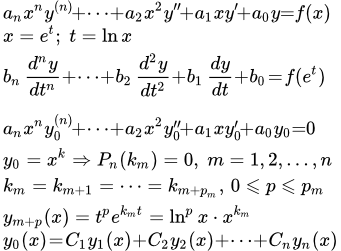Метод характеристического уравнения метод эйлера

Дифференциальное уравнение Эйлера и методы его решения

Более общее уравнение Эйлера имеет вид:
.
Это уравнение подстановкой t = ax+b приводится к более простому виду, которое мы и будем рассматривать.

Приведение дифференциального уравнения Эйлера к уравнению с постоянными коэффициентами.

Рассмотрим уравнение Эйлера:
(1) .
Оно сводится к линейному уравнению с постоянными коэффициентами подстановкой:
x = e t .
Действительно, тогда
;
;
;

;
;
.

Таким образом, множители, содержащие x m , сокращаются. Остаются члены с постоянными коэффициентами. Однако на практике, для решения уравнений Эйлера, можно применять методы решения линейных ДУ с постоянными коэффициентами без использования указанной выше подстановки.

Решение однородного уравнения Эйлера

Рассмотрим однородное уравнение Эйлера:
(2) .
Ищем решение уравнения (2) в виде
.
;
;
.
.
Подставляем в (2) и сокращаем на x k . Получаем характеристическое уравнение:
.
Решаем его и получаем n корней, которые могут быть комплексными.

Рассмотрим действительные корни. Пусть k_i – кратный корень кратности m . Этим m корням соответствуют m линейно независимых решений:
.

Рассмотрим комплексные корни. Они появляются парами вместе с комплексно сопряженными. Пусть k_i – кратный корень кратности m . Выразим комплексный корень k_i через действительную и мнимую части:
.
Этим m корням и m комплексно сопряженным корням соответствуют 2 m линейно независимых решений:
;
;
.
.

После того как получены n линейно независимых решений, получаем общее решение уравнения (2):
(3) .

Примеры

Решение неоднородного уравнения Эйлера

Рассмотрим неоднородное уравнение Эйлера:
.
Метод вариации постоянных (метод Лагранжа) также применим и к уравнениям Эйлера.

Сначала мы решаем однородное уравнение (2) и получаем его общее решение (3). Затем считаем постоянные функциями от переменной x . Дифференцируем (3) n – 1 раз. Получаем выражения для n – 1 производных y по x . При каждом дифференцировании члены, содержащие производные приравниваем к нулю. Так получаем n – 1 уравнений, связывающих производные . Далее находим n -ю производную y . Подставляем полученные производные в (1) и получаем n -е уравнение, связывающее производные . Из этих уравнений определяем . После чего интегрируя, получаем общее решение уравнения (1).

Пример

Неоднородное уравнение Эйлера со специальной неоднородной частью

Рассмотрим уравнение Эйлера со специальной неоднородной частью:
(4)
,
где – многочлены от степеней и , соответственно.

Наиболее простой способ решения такого уравнения заключается в том, чтобы сделать подстановку
,
и решать линейное уравнение с постоянными коэффициентами со специальной неоднородной частью.

Автор: Олег Одинцов . Опубликовано: 14-08-2013 Изменено: 24-10-2020

Линейные неоднородные системы дифференциальных уравнений

Неоднородную систему дифуравнений обычно представляют в следующем виде:

В отличие от однородной системы, здесь в каждом уравнении добавляется некая функция, которая зависит от t. Функции f(t) и g(t) могут быть как const, exp, так и sin, cos и т.д.

Необходимо найти частное решение системы линейных дифуравнений
при начальных условиях x(0) = 6, y(0) = 5.

Итак, у нас есть линейная неоднородная система дифуравнений, где в качестве f(t) и g(t) выступают константы. Будем использовать метод исключения.

Выразим из первого уравнения системы:

Опять применим маркер * для выделения.

Обе части уравнения дифференцируем по t:

Производная const = 0, поэтому 3 исчезла.

Подставляем и во второе уравнение системы:

Избавимся от дробей, для чего обе части уравнения умножим на 5:

Итак, мы получили линейное неоднородное уравнение второго порядка с постоянными коэффициентами. Этим и отличается наше решение от решения однородной системы уравнений.

Но иногда, отметим, в неоднородной системе может получиться и однородное уравнение.

Находим общее решение однородного уравнения

Для этого необходимо составить и решить характеристическое уравнение:

– мы нашли сопряженные комплексные корни, поэтому:

.

Теперь займемся поиском частного решения неоднородного уравнения вида .

Находим первую и вторую производную:

Подставляем в левую часть неоднородного уравнения:

Получаем:

Это частное решение можно с легкостью подобрать устно и можно просто записать: «Очевидно, что частное решение неоднородного уравнения: ».

В итоге:

Найдем функцию y(t).

Для этого найдем производную от найденной функции x(t):

Подставляем и в уравнение (*):

Получаем общее решение системы:

Теперь найдем частное решение, соответствующее начальным условиям x(0) = 6, y(0) = 5:

Ответ: частное решение:

Метод характеристического уравнения (метод Эйлера)

Этот метод используется крайне редко, но мы все-же рассмотрим его на примере.

Дается линейная однородная система дифуравнений

Требуется отыскать общее решение системы уравнений методом Эйлера.

Составим определитель второго порядка:

Далее надо составить характеристическое уравнение, для чего из каждого числа, расположенного на главной диагонали, вычтем некий параметр k:

Получили квадратное уравнение. Найдем его корни:

В случае, когда характеристическое уравнение имеет 2 различных действительных корня, общее решение системы дифференциальных уравнений будет иметь вид:

Коэффициенты в показателях экспонент мы уже нашли, займемся поиском коэффициентов

Подставим корень в характеристическое уравнение:

Составим систему двух линейных уравнений из чисел определителя:

Из которой получаем:

Подберем наименьшее значение , при котором будет целым. Очевидней всего будет =5, тогда =7/5*5 = 7.

Подставим корень в характеристическое уравнение:

Составим систему двух линейных уравнений из чисел определителя:

Из которой получаем:

Подберем наименьшее значение , при котором будет целым. Очевидней всего будет .

Коэффициенты найдены, подставляем их в систему

Ответ: общее решение:

Chanel Allure (http://духи.рф/catalog/men/Chanel/Allure)
Есть много имен — женские имена русские (http://духи.рф/catalog/men/Chanel/Allure) поражают своей красотой и разнообразием.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

Метод характеристического уравнения метод эйлера

Variant 19 (Sukach Maxim, BS17-03)

Найдем

В итоге, наше решение принимает вид:

Метод Эйлера дает возможность приближенно выразить функцию теоретически с любой наперед заданной точностью. Суть метода Эйлера в пошаговом вычислении значений решения y=y(x) дифференциального уравнения вида y’=f(x,y) с начальным условием (x0;y0). Метод Эйлера является методом 1-го порядка точности и называется методом ломаных.

Для вычисления используются следующие формулы:

Метод Эйлера и точное решение при x0 = 0, xf = 9, y0 = 1, h = 0.1

Метод Эйлера и точное решение при x0 = 0, xf = 3, y0 = 1, h = 0.1

Метод Эйлера и точное решение при x0 = 0, xf = 1, y0 = 1, h = 0.1

Усовершенствованный метод Эйлера

Суть усовершенствованного метода Эйлера в пошаговом вычислении значений решения y=y(x) дифференциального уравнения вида y’=f(x,y) с начальным условием (x0;y0). Усовершенствованный метод Эйлера является методом 2-го порядка точности и называется модифицированным методом Эйлера.

Разница между данным методом и методом Эйлера минимальна и заключается в использовании следующих формул:

Усовершенствованный Метод Эйлера и точное решение при
x0 = 0, xf = 9, y0 = 1, h = 0.1

Усовершенствованный Метод Эйлера и точное решение при
x0 = 0, xf = 3, y0 = 1, h = 0.1

Усовершенствованный Метод Эйлера и точное решение при
x0 = 0, xf = 1, y0 = 1, h = 0.1

Классический метод Рунге-Кутты

Суть метода Рунге-Кутты в пошаговом вычислении значений решения y=y(x) дифференциального уравнения вида y’=f(x,y) с начальным условием (x0;y0). Классический метод Рунге-Кутты является методом 4-го порядка точности и называется методом Рунге-Кутты 4-го порядка точности.

Ну и как обычно, формулы:

Классический метод Рунге-Кутты и точное решение при x0 = 0, xf = 9, y0 = 1, h = 0.1

Классический метод Рунге-Кутты и точное решение при x0 = 0, xf = 3, y0 = 1, h = 0.1

Классический метод Рунге-Кутты и точное решение при x0 = 0, xf = 1, y0 = 1, h = 0.1

Сравнение методов для заданной задачи

Размер ошибки всех методов на промежутке [0, 9] с шагом 0.1

Размер ошибки всех методов на промежутке [0, 3] с шагом 0.1

Размер ошибки всех методов на промежутке [0, 1] с шагом 0.1

Очевидно что, классический метод Рунге-Кутты справляется с задачей аппроксимации в случае данного уравнения намного лучше чем Метод Эйлера и Усовершенствованный метод Эйлера.

График глобальной средней ошибки

Глобальная ошибка в зависимости от размера шага H на промежутке от 0.01 до 0.91 для x0 = 1, xf = 9