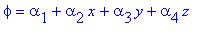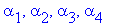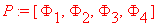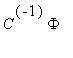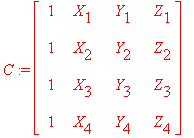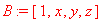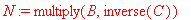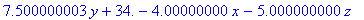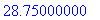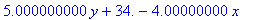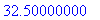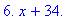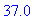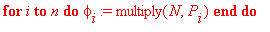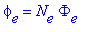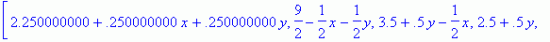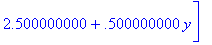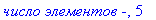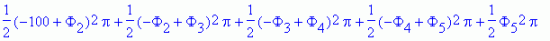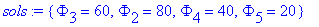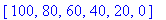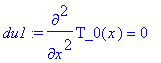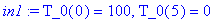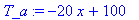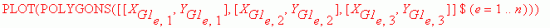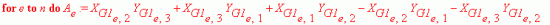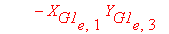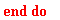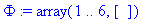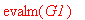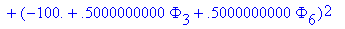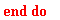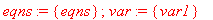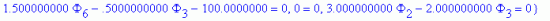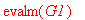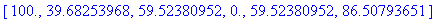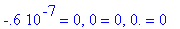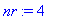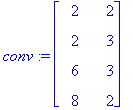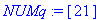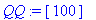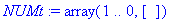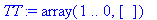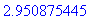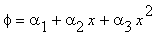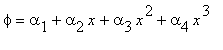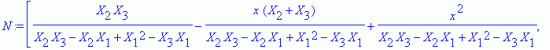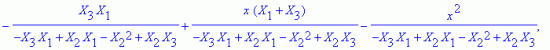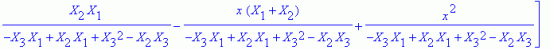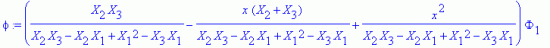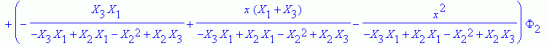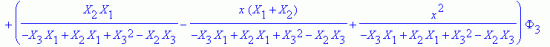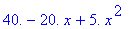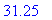Метод конечных элементов для уравнения лапласа

Метод конечных элементов для уравнения лапласа

Метод конечных элементов основан на идее аппроксимации непрерывной функции (в физической интерпретации — температуры, давления, перемещения и т.д.) дискретной моделью, которая строится на множестве кусочно-непрерывных функций, определенных на конечном числе подобластей, называемых конечными элементами. Исследуемая геометрическая область разбивается на элементы таким образом, чтобы на каждом из них неизвестная функция аппроксимировалась пробной функцией (как правило, полиномом). Причем эти пробные функции должны удовлетворять граничным условиям непрерывности, совпадающим с граничными условиями, налагаемыми самой задачей. Выбор для каждого элемента аппроксимирующей функции будет определять соответствующий тип элемента.

В данной работе рассматривается вычислительный алгоритм метода конечных элементов в формулировке, основанной на процедуре минимизации функционала, соответствующего решаемой непрерывной задаче [1]. В результате выполнения указанной процедуры происходит замещение уравнения или системы уравнений в частных производных системой недифференциальных уравнений, имеющих в качестве коэффициентов аппроксимирующие функции, которые фактически являются значениями искомой функции в вершинах разбиения.

При построении алгоритма используется математический аппарат, предоставляемый системой Maple [2,3].

Линейные интерполяционные полиномы

Рассмотрим особенности построения линейных интерполяционных соотношений, соответствующих симплекс-элементам [4].

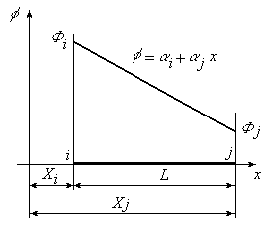
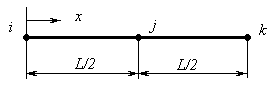
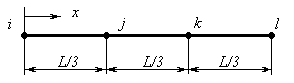
— одномерный симплекс-элемент, представляющий собой прямолинейный отрезок длины L с двумя узлами, по одному на каждом конце;

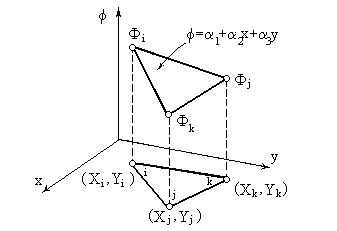
— двумерный симплекс-элемент. Это треугольник с прямолинейными сторонами и тремя узлами, по одному в каждой вершине;

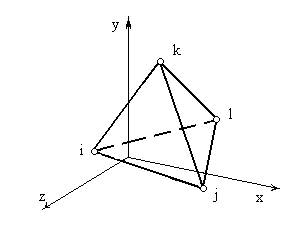
— трехмерный симплекс-элемент. Он представляет собой тетраэдр. Четыре его узла обозначены индексами i,j,k,l, причем обход узлов i,j,k осуществляется в том порядке, как они записаны, против часовой стрелки. Узел l расположен в вершине, находящейся вне плоскости узлов i,j,k.

В общем (трехмерном) случае линейный интерполяционный полином для симплекс-элемента имеет вид [2]:

(В двумерном случае z = 0, а в одномерном — z = 0 и y = 0.)

с помощью известных значений искомой функции в узловых точках.

>

из решения матричного уравнения

=

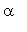
где С — следующая матрица

>

Объединив в матрицу В множители при 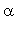в интерполяционнной формуле

>

получим матрицу так называемых функций формы (базисных функций), вычисляемую как

>

Тогда интерполяционный полином для искомой функции может быть получен следующей операцией

>

Рассмотрим трехмерный симплекс-элемент, используемый для аппроксимации распределения непрерывной функции внутри тетраэдра.

Вначале определяем массивы численных данных с известными координатами четырех узлов (см. рис):

Отобразим этот тетраэдр на экране дисплея

[X[2],Y[2],Z[2]],
[X[1],Y[1],Z[1]]],
axes=boxed,orientation =[-160,-100], shading=XY,style=PATCHCONTOUR,light=[20,10,5,3,1],lightmodel=’light3′);

Пусть значениями функции в соответствующих узловых точках будут

>

Тогда искомый интерполяционный полином примет вид

Во внутренней точке с координатами (1, 0.5, 1) имеем значение функции

Аналогично получим полином, соответствующий двумерному симплекс-элементу:

> P := [Phi[1], Phi[2], Phi[3]]:

Определяем массивы численных данных:

Значения функции в соответствующих узловых точках

Искомый интерполяционный полином будет иметь вид

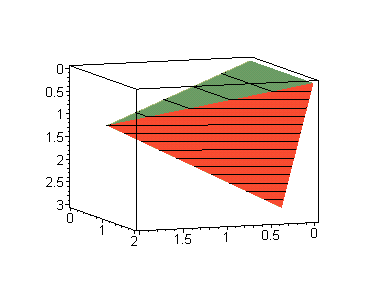
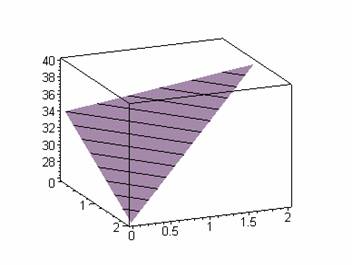
В отличие от трехмерного случая, полученную аппроксимирующую функцию можно представить наглядно:

> with(plots):
polygonplot3d([
[X[1],Y[1],Phi[1]],
[X[2],Y[2],Phi[2]],
[X[3],Y[3],Phi[3]]],axes=boxed,style =PATCHCONTOUR);

В точке с координатами (1, 0.5) имеем значение

Теперь для одномерного симплекс-элемента:

> restart: with (linalg ):

Массивы численных данных:

значения функции в соответствующих узловых точках

Искомый интерполяционный полином:

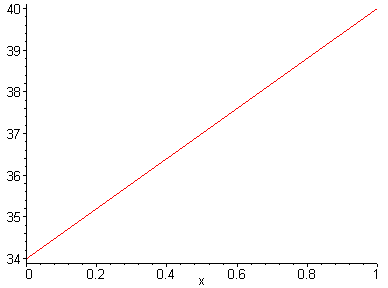
Изображаем его на графике:

В точке с координатой х = 0.5 имеем значение искомой функции

В данной работе интерполяционные соотношения использованы при рассмотрении скалярной величины. При интерполировании векторных величин, например перемещений в каждом узле необходимо определить более одной неизвестной (степени свободы). В этом случае векторную величину можно представить ее компонентами, которые рассматриваются как неизвестные скалярные величины. Каждый узел будет содержать одну, две или три неизвестные в зависимости от того, какая задача рассматривается — одномерная, двумерная или трехмерная. Причем в одномерной задаче представления векторной и скалярной величин внутри элемента совпадают, так как в обоих случаях в каждом узле отыскивается только одна неизвестная:

В двумерной, трехмерной, или в общем случае n-мерной задаче необходимо аппроксимировать каждую компоненту неизвестной, например:

Узловые значения температуры для треугольного симплекс-элемента равны Ф=130, Ф=100, Ф=125. Выясните, где изотерма 125 пересекает границы элемента.

Линейные интерполяционные полиномы для дискретизованной области

Warning, the protected names norm and trace have been redefined and unprotected

В общем виде интерполяционный полином, полученный в п.1 будет иметь вид

где е — индекс, указывающий на отдельный элемент.

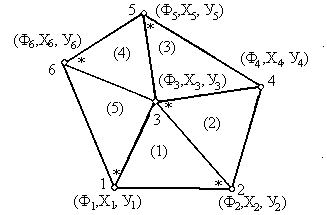
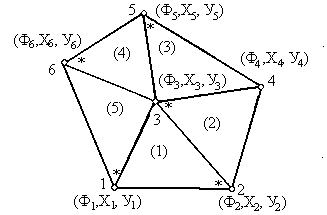
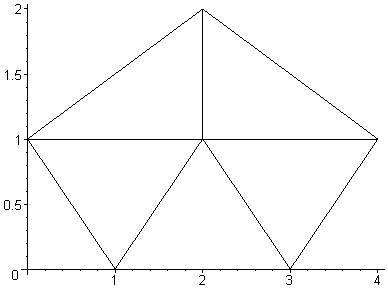
Технику включения двумерного элемента в область проиллюстрируем на примере простой пятиэлементной конфигурации, показанной на следующем рисунке

Определим числовые массивы координат пяти узлов и значений искомой функции в указанных точках:

и составим массив, характеризующий всю пятиугольную область:

Зададим вектор коэффициентов В (для вычисления базисных функций) и вектор phi , в котором будут накапливаться полиномы, аппроксимирующие непрерывную функцию внутри каждого элемента

Оформим цикл матричных вычислений

Вектор полученных полиномов имеет вид

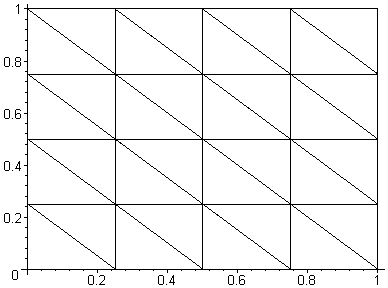
Изобразим картину распределения Ф на графике

> with(plots):
list_point :=
[
seq(
[
[G1[S,1],G1[S,2],G1[S,7]],
[G1[S,3],G1[S,4],G1[S,8]],
[G1[S,5],G1[S,6],G1[S,9]]
],
S=1..5)]:
polygonplot3d(list_point, scaling=UNCONSTRAINED, axes=FRAMED,
titlefont=[TIMES,ROMAN,12], shading=Z,labels=[x,y,phi], style=hidden,
orientation=[-50,40],lightmodel=light3);

Warning, the name changecoords has been redefined

Получите интерполяционные соотношения для элементов, составляющих область, показанную на рисунке, если заданы координаты точек дискретизации и значения искомой функции в них:

> X:=[0,2,4,0.25,3.75]: Y:=[0,0.25,0.51,2,2.75]: Phi:=[100,80,60,70,45]:

Изобразите ситуацию на графике.

Одномерная задача стационарной теплопроводности

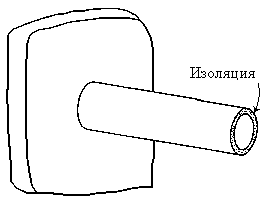
Рассмотрим одномерный поток тепла в стержне с теплоизолированной боковой поверхностью (рис.1).

Рис.1. Модель теплопроводности в стержне

В вариационном исчислении устанавливается, что для минимизации функционала

(1)

необходимо, чтобы удовлетворялось дифференциальное уравнение

(2)

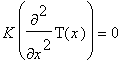
с граничными условиями

(3)

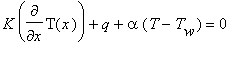
В формулах (1)-(3): Т — температура, К — коэффициент теплопроводности, q -тепловой поток заданной интенсивности, a — коэффициент конвективного теплообмена, T w — температура окружающей среды, V — объем стержня, S — площадь поперечного сечения стержня, х — координата вдоль оси стержня. Таким образом, любое распределение Т(х) , при котором функционал c (1) становится минимальным, является решением исходной задачи теплопроводности (2)-(3).

> with(linalg):
Представим стержень дискретной моделью, содержащей шесть узловых точек:
> m:=6:
Phi:=vector(m):
с координами
> X:=[0,1,2,3,4,5]:
Пусть площадь поперечного сечения стержня будет
> A:=Pi:
В граничных точках известны значения температуры:
> Phi[1]:=100:Phi[6]:=0:

Следующая часть программного кода формирует рабочий массив данных G1

> for i to m do
q[i]:=0: alpha[i]:=1: Tw[i]:=0:
od:
n:=m-1:
G1:=array(1..n,1..11):
for i to n do
K[i]:=1:
G1[i,1]:=X[i]: G1[i,2]:=X[i+1]:
G1[i,3]:=Phi[i]: G1[i,4]:=Phi[i+1]:
G1[i,5]:=q[i]: G1[i,6]:=q[i+1]:
G1[i,7]:=alpha[i]:G1[i,8]:=alpha[i+1]:
G1[i,9]:=Tw[i]: G1[i,10]:=Tw[i+1]:G1[i,11]:=K[i]:
od:
print (`число элементов -` ,n);

В отдельных узлах можно задать тепловой поток (по умолчанию для остальных i узлов q[i]=0)

В узлах контактирующих с окружающей средой можно задать температуру последней T w (по умолчанию T w [i]=0) и известные коэффициенты теплоотдачи окружающей среде (по умолчанию alpha[i]=1)

Также можно ввести коэффициенты теплопроводности в отдельных элементах (по умолчанию K[j]=1)

В следующей ячейке автоматически вычисляются интерполяционные полиномы и функционалы для каждого из n отдельных элементов, в результате получается суммарный функционал.

> B:=vector([1,x]):
eqns:=NULL:ch:=0:
for e to n do
C:=matrix([[1,G1[e,1]],
[1,G1[e,2]] ]):
N:=multiply(B,inverse(C)):
P:=([G1[e,3],G1[e,4]]):
phi:=multiply(N,P):
chi:=int((1/2)*K[e]*(diff(phi,x))^2*A,x=G1[e,1]..G1[e,2]):
if q[e] 0 or q[e+1] 0 then
chi:=chi+sum( ‘int(q[k]*Phi[k],s=0..A)’,’k’=e..e+1):
fi:
if Tw[e] 0 or Tw[e+1] 0 then
chi:=chi+sum(‘int((alpha[k]/2)*(Phi[k]-Tw[k])^2,s=0..A)’,
‘k’=e..e+1):
fi:
ch:=ch+chi:
od:
ch;

Далее осуществляется минимизация функционала
> var1:=NULL:
for e to m do
if type(Phi[e],integer) then
eq1:=0=0
else
eq1:=diff(ch,Phi[e])=0:
var1:=var1,Phi[e]:
fi:
eqns:=eqns,eq1:
od:
Формируется система линейных алгебраических уравнений
> eqns:=:var:=:
решение которой дает неизвестные значения температуры в узлах:
> sols := solve( eqns,var);

Для построения графика понадобится процедура сортировки вычисленных значений
> sorty:=proc(Phi,sols,m)
local i,j:
for i to nops(sols) do
for j to m do
if Phi[j] op(1,sols[i]) then next
else Phi[j]:=op(2,sols[i])
fi:
od:
od:
end:
sorty(Phi,sols,m):
evalm(Phi);
evalm(G1):

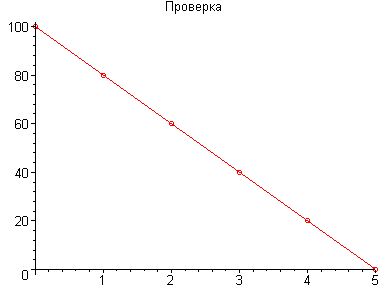
А теперь непосредственно график

> with(plots): f_1:=plot([seq([X[i], Phi[i]], i = 1 .. nops(X))], style = point, symbol = circle, color = red):display(f_1);

Рассмотренное решение простого примера может быть легко проверено аналитически с помощью средств Maple. Задаем дифференциальное уравнение и граничные условия
> with(DEtools):
du1:=diff(T_0(x),x,x)=0;
in1:=T_0(0)=100,T_0(5)=0;

Теперь определяем параметры графика
> f_2:=plot(T_a,x=0..5,title=`Проверка`):
и изображаем полученные численное и аналитическое решение на одном чертеже
> display();

В данной задаче аналитическое и численное решения полностью совпадают.

Найдите численное решение рассмотренной задачи, если

Двумерная задача стационарной теплопроводности

4.1. Постановка задачи

Warning, the protected names norm and trace have been redefined and unprotected

Рассмотрим задачу теплопроводности в двумерной постановке.
С вариационной точки зрения отыскание минимума функционала

(4.1)

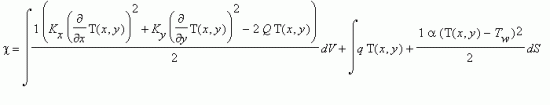
эквивалентно решению дифференциального уравнения теплопроводности

(4.2)

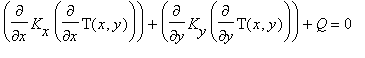
с граничными условиями

(4.3)

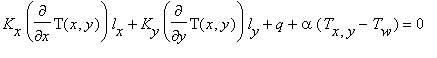
В формулах (4.1)-(4.3): Т — температура, К — коэффициент теплопроводности, q -тепловой поток заданной интенсивности, Q — внутренний тепловой источник или сток, a — коэффициент конвективного теплообмена, T w — температура окружающей среды, l — направляющие косинусы вектора нормали к поверхности,

V — объем, S — площадь поверхности, х,у — координаты.

Таким образом, любое распределение Т(х,у) , при котором функционал c (1) становится минимальным, является решением исходной задачи теплопроводности (2)-(3).

4.2. Описание геометрии области определения в симплекс-элементах

Пусть рассматривается область структуры, аналогичной геометрии из раздела 2 (рис.4.1).

Задаем число узловых точек
> m:=6:
и число элементов
> n:=5:
Вводим координат узловых точек
> X:=[1,3,2,4,2,0]: Y:=[0,0,1,1,2,1]:
Данные о структуре области могут быть представлены номерами узлов каждого из элементов, которые вводятся в обходе по часовой стрелки, начиная с узла, помеченного на рисунке звездочкой.
> G1:=array(1..n,1..25,
[
[2,3,1],
[3,2,4],
[5,3,4],
[6,3,5],
[1,3,6]
]):

Построим изображение расчетной сетки

Вычислим площади каждого из элементов

4.3. Описание физических свойств расчетной области

Определим параметры по умолчанию
> Phi:=vector(m);

for i to m do
q[i]:=0: Q[i]:=0: alpha[i]:=1: Tw[i]:=0:
od:

Зададим известные узловые температуры:
> Phi[1]:=100.:Phi[4]:=.0:
Зададим известные тепловые потоки в узлах расчетной сетки:
> Q[3]:=-10:
Можно задать известные температуры окружающей среды для элементов, с ней контактирующих (например, Tw[2]=20)
>
и соответствующие коэффициенты теплоотдачи окружающей среде
(например alpha[2]=5)
>
Коэффициенты теплопроводности отдельных элементов могут быть отличными от принятых по умолчанию (например K[3]=1.3)

Сформируем рабочий массив данных

>

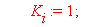
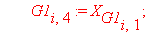
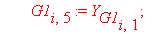
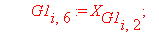
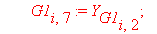
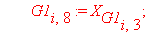
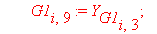
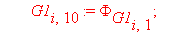
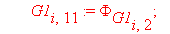
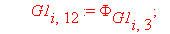
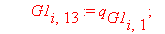
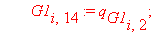
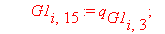
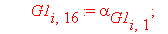
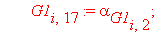
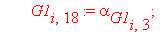
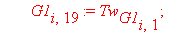
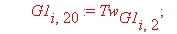
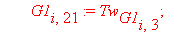
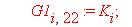
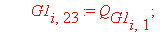
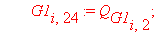
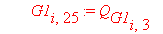
Следующий фрагмент программного кода производит автоматическое вычисление интерполяционных полиномов и функционалов для каждого из n отдельных элементов. В итоге получается суммарный функционал, характеризующий задачу.
> B:=vector([1,x,y]):
eqns:=NULL:ch:=0:
for e to n do
C:=matrix([[1,G1[e,4],G1[e,5]],
[1,G1[e,6],G1[e,7]],
[1,G1[e,8],G1[e,9]] ]):
N:=multiply(B,inverse(C)):
P:=([G1[e,10],G1[e,11],G1[e,12]]):
phi:=multiply(N,P):
chi:=int((1/2)*(K[e]*((diff(phi,x))^2+K[e]*(diff(phi,y))^2)*A[e]),z=0..1):
if G1[e,23] 0 or G1[e,24] 0 or G1[e,25] 0 then
chi:=chi-sum( ‘int((1/2)*G1[e,k]*G1[e,k-13],z=0..1)’,’k’=23..25):
fi:

if G1[e,13] 0 or G1[e,14] 0 or G1[e,15] 0 then
chi:=chi+sum( ‘int(G1[e,k]*G1[e,k-3],s=0..A[e])’,’k’=13..15):
fi:
if G1[e,19] 0 or G1[e,20] 0 or G1[e,21] 0 then
chi:=chi+sum(‘int((G1[e,k-3]/2)*(G1[e,k-9]-G1[e,k])^2,s=0..A[e])’,
‘k’=19..21):
fi:
ch:=ch+chi:
od:
ch;

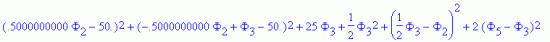
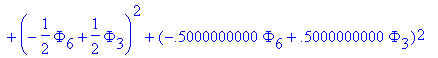
Осуществляем минимизацию функционала

>

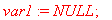
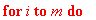
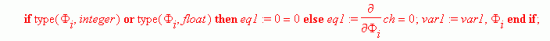
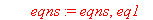
Формируем итоговую систему линейных алгебраических уравнений (СЛАУ)

>

>

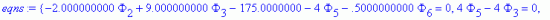
Таким образом получены неизвестные значения температуры в соответствующих узлах:

Процедура сортировки и вывод итогового вектора узловых значений

>

>

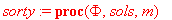
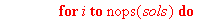
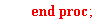
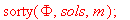
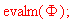
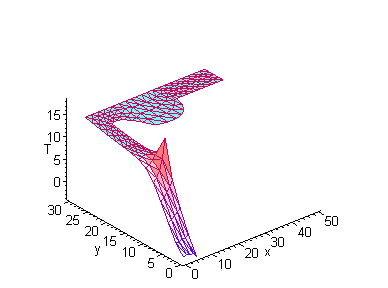
Построим график распределения температуры

> with(plots):
list_poy := [seq([
[G1[S,4],G1[S,5],G1[S,10]],
[G1[S,6],G1[S,7],G1[S,11]],
[G1[S,8],G1[S,9],G1[S,12]]
],S=1..n)]:
polygonplot3d(list_poy, scaling=UNCONSTRAINED, axes=FRAMED,
titlefont=[TIMES,ROMAN,12], shading=ZGREYSCALE,labels=[x,y,T],
style=PATCHCONTOUR, orientation=[-20,70]);

Для некоторых достаточно тонких элементов конструкций изменением температуры по толщине можно пренебречь. Однако для таких элементов значительное влияние оказывает теплообмен с окружающей средой вдоль лицевых поверхностей.

Найдите распределение температуры для геометрической области рассматриваемой в данном разделе, если происходит подобная теплоотдача при температуре окружающей средыTw=20, а коэффициент конвективного теплообмена alpha=20. Коэффициент теплопроводности всей области в целом считать равным К=15.

Сравнение с аналитическим решением

В добавление к обычным ошибкам округления и аппроксимации, свойственным почти любой вычислительной процедуре в методе конечных элементов имеют место:
а) ошибки, являющиеся результатом геометрических различий границы области определения и ее конечно-элементным приближением;
б) ошибки, обусловленные разницей между точным решением задачи в частных производных и его представлением пробной функцией.
> restart:
with(linalg):
with(plots):
FIG:= array(1..2):

Warning, the protected names norm and trace have been redefined and unprotected
Warning, the name changecoords has been redefined

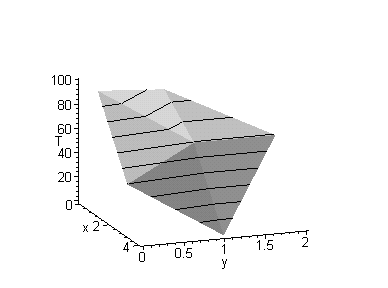
Рассмотрим решение уравнения Лапласа (уравнение 4.2 с нулевой правой частью) на единичном квадрате с граничными условиями, указанными на рисунке.

При решении задачи методом конечных элементов используем процедуры, описанные в п.4.
Принятое число узловых точек — 25, число элементов -32.
> m:=25:
> n:=32:
Координаты узловых точек
> X:=[0,0.25,0.5,0.75,1,
0,0.25,0.5,0.75,1,
0,0.25,0.5,0.75,1,
0,0.25,0.5,0.75,1,
0,0.25,0.5,0.75,1]:
Y:=[0,0,0,0,0,
0.25,0.25,0.25,0.25,0.25,
0.5,0.5,0.5,0.5,0.5,
0.75,0.75,0.75,0.75,0.75,
1,1,1,1,1]:

Структура области.
> G1:=array(1..n,1..25,
[
[1,2,6], [2,7,6], [2,3,7],[3,8,7],[3,4,8],[4,9,8],[4,5,9],[5,10,9],
[6,7,11],[7,12,11],[7,8,12],[8,13,12],[8,9,13],[9,14,13],[9,10,14],
[10,15,14],[11,12,16],[12,17,16],[12,13,17],[13,18,17],[13,14,18],
[14,19,18],[14,15,19],[15,20,19],[16,17,21],[17,22,21],[17,18,22],
[18,23,22],[18,19,23],[19,24,23],[19,20,24],[20,25,24]
]):
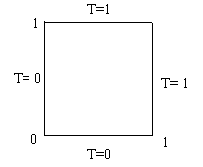
Конечно-элементная расчетная сетка
> PLOT(POLYGONS([[X[G1[e,1]],Y[G1[e,1]]], [X[G1[e,2]],Y[G1[e,2]]], [X[G1[e,3]],Y[G1[e,3]]] ] $e=1..n));

Параметры по умолчанию
> Phi:=vector(m):
for i to m do
q[i]:=0: Q[i]:=0: alpha[i]:=1: Tw[i]:=0:
od:
Ввод известных значений функции в точках на границе
> Phi[1]:=0.:Phi[2]:=.0:Phi[3]:=0:Phi[4]:=0: Phi[5]:=0.5:
Phi[6]:=0.:Phi[15]:=1.:Phi[11]:=0.:Phi[20]:=1.:
Phi[16]:=0.:Phi[10]:=1.:
Phi[21]:=0.5:Phi[22]:=1:Phi[23]:=1:Phi[24]:=1:Phi[25]:=1.:
Расчетный блок конечно-элементного метода
> for e to n do
A[e]:=(X[G1[e,2]]*Y[G1[e,3]]+X[G1[e,3]]*Y[G1[e,1]]+
X[G1[e,1]]*Y[G1[e,2]]-X[G1[e,2]]*Y[G1[e,1]]-X[G1[e,3]]*
Y[G1[e,2]]-X[G1[e,1]]*Y[G1[e,3]]):

if G1[e,23] 0 or G1[e,24] 0 or G1[e,25] 0 then
chi:=chi-A[e]*sum( ‘int((1/2)*G1[e,k]*G1[e,k-13],z=0..1)’,’k’=23..25):
fi:

if G1[e,13] 0 or G1[e,14] 0 or G1[e,15] 0 then
chi:=chi+sum( ‘int(G1[e,k]*G1[e,k-3],s=0..A[e])’,’k’=13..15):
fi:

if G1[e,19] 0 or G1[e,20] 0 or G1[e,21] 0 then
chi:=chi+sum(‘int((G1[e,k-3]/2)*(G1[e,k-9]-G1[e,k])^2,s=0..A[e])’,
‘k’=19..21):
fi:

var1:=NULL:
for i to m do
if type(Phi[i],integer) or type(Phi[i],float) then
eq1:=0=0
else
eq1:=diff(ch,Phi[i])=0:
var1:=var1,Phi[i]:
fi:
eqns:=eqns,eq1:
od:

sorty:=proc(Phi,sols,m)
local i,j:
for i to nops(sols) do
for j to m do
if Phi[j] op(1,sols[i]) then next
else Phi[j]:=op(2,sols[i])
fi:
od:
od:
end:
sorty(Phi,sols,m):
evalm(Phi):
evalm(G1)

Матрица найденных значений для неизвестных узлов
> T_num:=matrix([[Phi[7],Phi[8],Phi[9]],
[Phi[12],Phi[13],Phi[14]],
[Phi[17],Phi[18],Phi[19]]]);

Описание графического представления матрицы решений
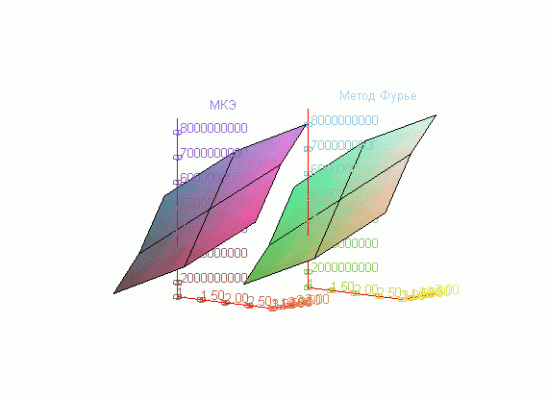
> FIG[1]:=matrixplot(T_num,axes=FRAMED,style=PATCHCONTOUR,title=`МКЭ`,labels=[x,y,T], orientation=[-10,90]):
Аналитическое решение выполним по методу Фурье, который заключает в себе разделение переменных и применение принципа суперпозиции. При этом разыскивается так называемое формальное решение, т.е. решение в виде бесконечного ряда, в котором каждый член есть решение уравнения Лапласа и удовлетворяет поставленным граничным условиям.
Число внутренних узлов по каждой из осей координат
> Nn:=3:
Число членов ряда, используемых для построения решения
> Ns:=40:
Блок вычислений по методу Фурье
> tt:=1/(Nn+1):p:=1: q:=1:
a:=array(1..Ns):b:=array(1..Ns):
for n from 1 to Ns do
a[n]:=sqrt(2/p)*int(0*sin(Pi*n*x),x=0..1):
b[n]:=sqrt(2/p)*int(1*sin(Pi*n*x),x=0..1):
od:

u:=array(1..Nn,1..Nn):
for i from 1 to Nn do
for j from 1 to Nn do trew:=sum(‘sin(Pi*k*i*tt)/sinh(Pi*k*q)*(a[k]*sinh(Pi*k*(1-j*tt))+b[k]*sinh(Pi*k*j*tt))’, ‘k=1..Ns’):
u[i,j]:=sqrt(2)*trew:
od:
od:

for n from 1 to Ns do
a[n]:=sqrt(2/p)*int(0*sin(Pi*n*y),y=0..1):
b[n]:=sqrt(2/p)*int(1*sin(Pi*n*y),y=0..1):
od:

u1:=array(1..Nn,1..Nn):
for i from 1 to Nn do
for j from 1 to Nn do trew:=sum(‘sin(Pi*k*j*tt)/sinh(Pi*k*q)*(a[k]*sinh(Pi*k*(1-i*tt))+b[k]*sinh(Pi*k*i*tt))’, ‘k=1..Ns’):
u1[i,j]:=sqrt(2)*trew:
od:od:

Матрица значений, найденных по методу Фурье, в точках области, соответствующих конечно-элементному разбиению
> T_anal:=evalf(evalm(u+u1));

Описание графического представления матрицы решений по методу Фурье
> FIG[2]:=matrixplot(T_anal,axes=FRAMED,style=PATCHCONTOUR,title=`Метод Фурье`,labels=[x,y,T], orientation=[-10,90]):
Общий характер решения по двум методам
> display(FIG);

Матрица относительных ошибок для найденных значений непрерывной функции в узлах разбиения (проценты)
> fd:=evalm(abs(T_num-T_anal)):mer:=matrix(3,3):
for i to 3 do
for j to 3 do
mer[i,j]:=100*fd[i,j]/T_anal[i,j]
od:
od:
evalm(mer);

Таким образом, максимальная относительная погрешность алгоритма метода конечных элементов в сравнении с аналитическим решением по методу Фурье не превысила 5.1 %.
При измельчении расчетной сетки и приближении треугольного конечного элемента по форме к равностороннему, численное решение, как правило, стремиться к уточнению.

Автоматическая генерация расчетной сетки и пример расчета температурного поля в области сложной формы

Процедуры автоматического получения расчетной сетки могут быть основаны на различных геометрических соображениях и принципах, как правило, не имея при этом глубокого теоретического обоснования. Главная их цель — выработать структуру исходных данных для последующего расчета.
Все процедуры, задействованные в этом рабочем документе, объединены в пакет h_FEM и считываются с жесткого диска в следующей командной ячейке:
> read»d:/МКЭ/h_FEM.m»:
Загрузим пакеты, необходимые в дальнейшем
> with(plots):with(h_FEM):
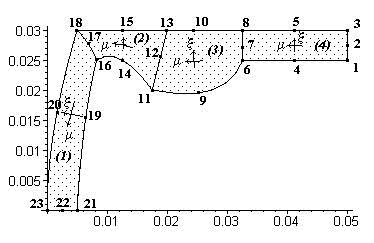
В рассматриваемом примере исходная область определения разбивается предварительно (в ручную) на четыре четырехугольных зоны (подобласти), имеющие общие стороны, как показано на следующем рисунке.

Нумерация узлов, используемых для задания четырехугольных зон, также как и самих зон произвольна.
Число зон задает переменная INRG, а число граничных точек — переменная INBP.
> INRG:=4: INBP:=23:
Координаты граничных точек в порядке их нумерации заносятся в массив XYP
> XYP:=array(1..INBP,1..2, [
[50,25],[50,27.5],[50,30],[41.25,25],[41.25,30],
[32.5,25],[32.5,27.5],[32.5,30],[27.5,20],[26.25,30],
[17.5,20],[18.75,25],[20,30],[12.5,25],[12.5,30],
[8.25,25],[7.,27.5],[5,30],[6.25,14],[1.25,14],
[5,0],[2.5,0],[0,0]
]):
В каждой подобласти, для того чтобы была возможность приписывать узлам, расположенным вдоль общей границы одни и те же номера, введена местная система координат xm , ориентация которой влияет на структуру матрицы итоговой системы линейных алгебраических уравнений (ширину ее полосы).
Чем меньшая ширина полосы будет получена, тем эффективнее будет последующий процесс вычислений.
Данные о соединении зон вводятся в массив JT и состоят из чисел, представляющих собой номера каждой из сторон отдельной зоны. При этом стороны нумеруются следующим образом: (- m ) — первая сторона, ( x ) — вторая, ( m ) — третья, (- x ) — четвертая.
Первая строка массива JT (зона 1) показывает, что сторона 1 граничит с зоной 2.
Вторая строка (зона 2) — сторона 1 граничит с зоной 3, а сторона 3 граничит с зоной 1.
Третья строка (зона 3) — сторона 1 граничит с зоной 4, а сторона 3 граничит с зоной 2.
Четвертая строка (зона 4) — сторона 3 граничит с зоной 3.
> JT:=array(1..INRG,1..4,[
[2,0,0,0],
[3,0,1,0],
[4,0,2,0],
[0,0,3,0]]):
Данные зон вводятся в массив region. Структура данных в строке (на примере первой строки массива):
1 — номер зоны, 14 — число строк узлов в зоне, 5 — число столбцов узлов в зоне;
16,17,18,20,23,22,21,19 — номера узлов зоны в обходе против часовой стрелки,
т.е. начиная с узла с координатами — m , — x и двигаясь слева направо от — x к + x и сверху вниз от + m к — m .
> region:=array(1..INRG,1..11,[
[1, 14,5, 16,17,18,20,23,22,21,19],
[2, 7, 5, 11,12,13,15,18,17,16,14],
[3, 7, 5, 6, 7, 8, 10,13,12,11,9 ],
[4, 9, 5, 1, 2, 3, 5, 8, 7, 6, 4 ]]):
Начальные исходные данные передаются в процедуру сеточного разбиения grid,
которая возвращает результаты дискретизации
> grid():
`Ширина полосы матрицы системы уравнений`, 7
`Общее число элементов`, 264
`Общее число узлов`, 170
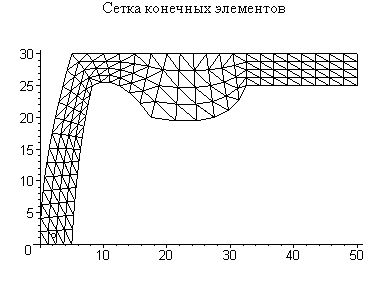
Сеточное разбиение можно визуализировать. При этом некоторый выбранный конечный элемент можно пометить на сетке кружком, для этого в качестве параметра команды v_rem() вводится номер этого элемента.
> v_rem(5):v_gr();
` Номер помеченного элемента`, 5
`Номера узлов помеченного элемента и их координаты:`
`Первый узел №`, 8, [2.615384615, 2.186390533]
`Второй узел №`, 9, [1.329696745, 2.105029586]
`Третий узел №`, 3, [2.50, 0.]
`Сторона 1 элемента образована узлами `, 8, `и`, 9
`Сторона 2 элемента образована узлами `, 9, `и`, 3
`Сторона 3 элемента образована узлами`, 3, `и`, 8

Далее исходные данные модифицируются для расчета температурного поля, т.е. задаются граничные условия и физические характеристики области. Та часть границы, на которой условия теплообмена не будут заданы,
по умолчанию теплоизолирована.
Массив conv заполняется для элементов, стороны которых участвуют в теплообмене с окружающей средой.
Число таких сторон определяет переменная nr
> nr:=4;

Структура двумерного массива conv следующая: conv [номер элемента, номер стороны].
В конвективном теплообмене может участвовать не более двух сторон одного элемента.
Если теплообмена со средой не происходит, все соответствующие данные остаются равными нулю.
> conv:=array(1..nr,1..2,[[2,2],[2,3],[6,3],[8,2]]);

Переменным H и TINF присваиваются значения соответственно коэффициента конвективного теплообмена [Вт/(м^2 К)] и температуры [градусы Цельсия] окружающей среды в точках поверхности конвективного теплообмена
> H:=5: TINF:=-5:
Переменным KXX и KYY присваиваются значения коэффициентов теплопроводности исходного материала соответственно вдоль координатных осей X и Y [Вт/м К].
> KXX:=10: KYY:=10:
Число узлов вычислительной сетки, в которых задана мощность теплового потока (UZq)
и известно значение температуры (UZt)
> UZq:=1: UZt:=0:
Номера узлов, в которых задана мощность теплового потока, заносятся в массив NUMq
> NUMq:=array(1..UZq,[21]);

Заданное значение мощности в узлах [Вт] заносятся в массив QQ

Номера узлов, в которых известно значение температуры заносятся в массив NUMt

Значения температуры [градусы Цельсия] в соответствующих узлах заносятся в массив TT

Данные перелаются в вычисляющую процедуру

Теперь из массива Xd можно вывести значение температуры в i-ом узле сетки, например:

> polygonplot3d(list_poy, scaling=UNCONSTRAINED,
axes=FRAMED,
titlefont=[TIMES,ROMAN,12],
shading=Z,labels=[x,y,T],
style=hidden,
orientation=[-130,50],
lightmodel=light3);

Воспользуйтесь пакетом процедур h_FEM для вычисления распределения температуры для области произвольной формы.

Элементы высокого порядка

Применение элементов высокого порядка, как правило, приводит к достижению заданной степени точности решения при меньшем количестве исходных данных. Однако оно не всегда ведет к сокращению полного времени счета; т.к. для составления матриц элемента необходимо использовать методы численного интегрирования, которые требуют выполнения большого числа арифметических операций.

Рассмотрим общую форму одномерного аппроксимирующего полинома.

Квадратичному элементу (с тремя узлами)

Коэффициенты полиномов можно определить аналогично линейному случаю с помощью заданных значений искомой функции в узлах, решая матричное уравнение a = .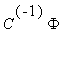

> restart: with(linalg):
Warning, the protected names norm and trace have been redefined and unprotected

Квадратичный интерполяционный полином будет равен

Пусть, например, даны:
координаты трех узлов
> X:=[0,1,2]:
и значения функции в них
> Phi:=[40,25.,20]:
Тогда искомый интерполяционный полином:
> phi;

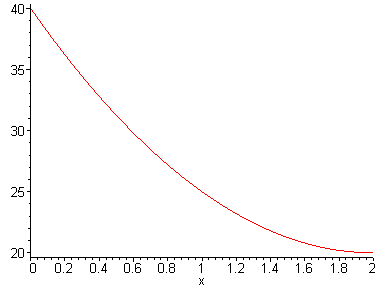
Изобразим его на графике.

В точке с координатой х = 0.5 имеем значение искомой функции

Показанный способ получения интерполяционных полиномов нетрудно распространить на другие элементы различных типов и размерностей. Использование при решении задач элементов высокого порядка аналогично использованию симплекс-элементов, поскольку выбор интерполяционного полинома не связан с исходными дифференциальными уравнениями.

Используйте элементы высокого порядка при решении одномерной задачи теплопроводности (п.3).

Получите квадратичный интерполяционный полином для конечного элемента, являющегося треугольником второго порядка

В методических указаниях рассмотрены особенности построения расчетных алгоритмов метода конечных элементов с использованием системы компьютерной математики Maple.