Метод конечных элементов для уравнения пуассона

МКЭ для уравнения Пуассона

Уравнение Пуассона — эллиптическое дифференциальное уравнение в частных производных, которое описывает:электростатическое поле, стационарное поле температуры, поле давления, поле потенциала скорости в гидродинамике.

Оно названо в честь знаменитого французского физика и математика Симеона Дени Пуассона.

Это уравнение имеет вид:

<\displaystyle \Delta \varphi =f,>Где <\displaystyle \Delta >— оператор Лапласа, или лапласиан, а <\displaystyle f>вещественная или комплексная функция на некотором многообразии.

<\displaystyle \Delta \varphi =0.>Уравнение Пуассона может быть решено с использованием функции Грина; см., например, статью экранированное уравнение Пуассона. Есть различные методы для получения численных решений. Например, используется итерационный алгоритм — «релаксационный метод».

Уравнение Пуассона (неоднородное уравнение Лапласа). Δ = fU (1) Область применения данного уравнения – задачи электростатики, электронной оптики, теории упругости и др.

В данной статье мне хотелось бы изложить реализацию метода конечных элементов на примере уравнения Пуассона. Рассмотрим задачу:

(2)

с однородным краевым условием

(3)

(4)

(5)

(6)

Требуется найти функцию , решающую заданное уравнение.

3.1 Решение
Умножим начальное уравнение на функцию , непрерывную, кусочно непрерывно-дифференцируемую и равную на краях нулю, и проинтегрируем полученное уравнение по всей области .
После применения формулы интегрирования по частям, получим следующее уравнение

(7)

Введем на области квадратную сетку с шагом :

(8)

и каждый квадрат разделим диагональю, параллельной биссектрисе первого координатного угла:

Получим разбиение области на треугольные элементы — триангуляция области . Триангуляция такого типа называется триангуляцией Фридрихса-Келлера.
Будем искать приближенное решение данного уравнения как функцию , равную нулю на границе (краевое условие), непрерывную на области и линейную на каждом полученном элементе триангуляции.
Функцию можно представить в следующем виде:
(9)

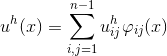
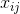
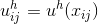
где значения функций в точке определены следующим образом:

(10)

(11)

Подставив функцию в первое уравнение, осуществив преобразования и вынос констант изпод знака интеграла, сведем задачу для каждой базисной функции к подсчету интегралов вида:

(12)

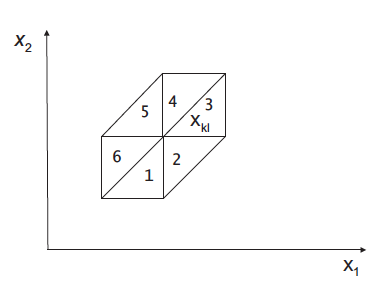
Значение интеграла может быть не нулевым лишь в том случае, если базисные функции под знаком интеграла имеют непустую общую область определения. По построению, каждый элемент имеет три вершины. Вершина может быть общей максимально для 6 треугольников:

С соответствующими значениями производных для каждого из 6 случаев приведенных в таблице 1:

После подсчетов интеграла уравнение с номером 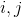будет выглядеть следующим образом:
(13)

(14)

и при достаточно малом :
(15)

Следовательно, уравнение может быть переписано в следующем виде:
(16)

Добавив граничные условия, а именно:

(17)

(18)

получаем полную СЛАР, решая которую, находим значения функции в точках сетки.

Выводы

Большая часть всех уравнений в частных производных 2 го порядка, линейных относительно вторых производных являются представителями 3 х различных классов уравнений, которые существенно отличаются друг от друга по методам исследования и по физической природе (описывают различные физические явления).

Любой процесс нагрева и охлаждения можно разделить на три стадии. Первая охватывает начало процесса и характеризуется постепенным распространением температурных возмущений, захватывающих все новые и новые участки материала.

Скорость изменения температуры в отдельных точках материала может быть различной и сильно зависит от начального распределения температур в теле и удаленности этих точек от источника нагрева или охлаждения.

Поэтому первая стадия процесса называется неупорядоченным режимом. С течением времени влияние начальных неравномерностей сглаживается, и относительная скорость изменения температуры во всех точках тела становится постоянной.

Наступает вторая стадия – режим упорядоченного процесса, который называют регулярным режимом.

Список литературы

1.Методические указания по выполнению лабораторных работ по теп-лотехнике. Северо-Западный заочный технический университет. – СПб, 2003. 2.Техническое описание лабораторного комплекса ЛКТ – 2А. – М.: Московский инженерно-физический институт, Владис, 1999. – 65 с.

3.Теплотехнический эксперимент. Справочник по тепломассообмену. – М.: Энергоиздат, 1982. – 512 с.

4.Исаев С.И. Теория тепломассообмена/ С.И. Исаев. – М.: Энергия,

5. Бахвалов Н. С., Корнев А. А., Чижонков Е. В. – Численные методы. Решения задач и упражнения. – М.: «Дрофа», 2009 г. 393 с. (Главы 2, 7, 9).

6.Вабищевич П. Н. – Вычислительные методы математической физики. Стационарные задачи. – М.: «Вузовская книга», 2008 г. 196 с.

7.Вабищевич П. Н. – Вычислительные методы математической физики. Нестационарные задачи. – М.: «Вузовская книга», 2008 г. 228 с.

8. Вержбицкий В. М. – Основы численных методов. – М.: «Высшая шко- ла», 2002 г. 840 с. (Главы 2, 3, 17, 19, 20, 21).

9. Власова Е. А., Зарубин В. С., Кувыркин Г. Н. – Приближенные методы математической физики. – М.: МГТУ им. Н. Э. Баумана, 2004 г. 704 с.

10.Зализняк В. Е. – Основы вычислительной физики. Часть 1: Введение в конечно-разностные методы. – М.: «Техносфера», 2008 г. 224 с

Метод конечных элементов. решение плоской задачи

Метод конечных элементов. Решение плоской задачи

4.1. Содержание метода.

Метод конечных элементов (MKЭ) представляет собой эффективный численный метод решения инженерных и физических задач. Он широко применяется при проектировании судов, летательных аппаратов, несущих систем многоэтажных зданий и т. п. Для МКЭ характерна ясная физическая трактовка. Его можно рассматривать, в частности, как обобщение классического метода строительной механики — метода перемещений. С другой стороны МКЭ является своеобразной формой часто применяемого вариационного метода Ритца. Различие между традиционной формой метода Ритца и МКЭ состоит в выборе системы координатных функций. Если в методе Ритца функции (обычно ряды) задаются для всей области, то в МКЭ они задаются для ее частей и через множество этих функций определяется состояние системы.

Классический подход к задаче об изучении напряженно-деформированного состояния диска (рис. 4.1) предполагает изучение бесконечно малого его элемента. Получающиеся при этом дифференциальные уравнения в частных производных (равновесия и геометрические) совместно с физическими уравнениями и контурными условиями позволяют определить напряжения, деформации и перемещения в каждой точке диска.

Метод конечных элементов предполагает иной подход. Рассматривается элемент конечных размеров, за счет чего осуществляется переход от сплошной системы с бесконечным числом степеней свободы, к системе с конечным числом степеней свободы.

Разделим воображаемыми линиями диск, изображенный на рис. 4.1, на некоторое количество элементов конечных размеров, например, треугольной формы и примем за узловые точки их вершины. Очевидно, что если диск находится в равновесии то и его элемент, определенный узлами i, j, k, под воздействием напряжений (усилий) от смежных элементов, также уравновешен. Приложим затем к е-му элементу вместо фактических усилий, действующих вдоль его граней статически эквивалентные узловые силы, т. е. силы, вызывающие внутри элемента действительное напряженно-деформированное состояние (рис. 4.2.).

Поставив в соответствие каждому узловому усилию узловое перемещение (рис. 4.2, (б)) представим сплошной диск набором конечных элементов, взаимодействующих между собой в конечном числе узловых точек.

Такой подход позволяет в дальнейшем использовать один из известных классических методов строительной механики, например метод перемещений (возможно также применение метода сил, либо смешанного). Для этого необходимо установить матрицы жесткости всех конечных элементов и, из условия равновесия узлов, получить разрешающие уравнения задачи. Найденные узловые перемещения не дают, однако, полной характеристики напряженно-деформированного состояния диска. Необходим переход от этих величин к перемещениям, напряжениям и деформациям внутри конечных элементов, т. е. речь идет о решении плоской задачи для каждого конечного элемента, находящегося под воздействием узловых перемещений. Такой переход в МКЭ осуществляется приближенно, путем задания интерполяционных (координатных) функций (функций формы), что и делает метод приближенным. Функции эти (обычно полиномы) такие, что обеспечивают неразрывность перемещений при переходе от одного элемента к другому.

Естественно, что при реализации МКЭ возникает необходимость приведения действующих на конструкцию нагрузок к сосредоточенным узловым силам.

Обычно все зависимости, связанные с конечным элементом, строятся в местной системе координат, с последующим переходом в общую систему для всей области. Это позволяет заранее получить необходимые соотношения для часто применяемых типов конечных элементов.

Решение задач по методу конечного элемента содержит следующие этапы:

1. Разбиение заданной области на конечные элементы. Нумерация узлов и элементов.

2. Построение матриц жесткости конечных элементов.

3. Сведение нагрузок и воздействий, приложенных к конечным элементам, к узловым силам.

4. Формирование общей системы уравнений; учет условий закрепления. Решение системы уравнений.

5. Определение напряжений и (при необходимости) деформаций в. конечных элементах.

4.2. Дискретизация области.

Разбиение области на подобласти представляет собой первый шаг на пути к решению задачи, и именно этот шаг не имеет теоретического обоснования. Искусство разбиения области зависит от имеющихся инженерных навыков. Плохое или несовершенное разбиение будет приводить к ошибочным результатам, если даже остальные этапы метода осуществляются с достаточной точностью.

Дискретизация области (тела) включает задание числа, размеров и формы подобластей, которые используются для построения дискретной модели реального тела. При этом, с одной стороны, элементы должны быть выбраны достаточно малыми, чтобы получить приемлемые результаты, а с другой стороны, применение достаточно крупных элементов сокращает вычислительную работу. Нужно иметь некоторые общие соображения об окончательных результатах, с тем, чтобы можно было уменьшить размеры элементов в тех областях, где ожидаемый результат может сильно меняться.

При решении задач методом конечных элементов используются элементы различных типов. Наиболее распространенные типы элементов приведены в табл. 4.1. Ниже будут рассматриваться в основном трехузловые треугольные КЭ, как наиболее простые и чаще других применяемые для решения плоской задачи.