Метод конечных элементов для уравнения теплопроводности

Метод конечных элементов в задачах теплопроводности (стр. 1 )

Из за большого объема эта статья размещена на нескольких страницах:
1 2 3 4 5 6 7 8

ГЛАВА 1. КРАЕВЫЕ ЗАДАЧИ ТЕОРИИ ПОЛЯ …………………. ………………10

1.1 Уравнение переноса в обобщенной криволинейной системе

1.2 Краевые условия задачи ……..…………………………. ……………15

1.3 Краткая характеристика методов решения краевой задачи …………17

ГЛАВА 2. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ В КРАЕВЫХ

2.1 Методы взвешенных невязок ..………………………………………. 20

2.2 Основная концепция метода конечных элементов …. ……. ……….24

ГЛАВА 3. ГЕОМЕТРИЧЕСКИЕ АСПЕКТЫ МКЭ ………………. ………………32

3.1 Базовый каталог конечных элементов …..……….…………. ……….32

3.2 Дискретизация области на элементы. ……………………. ………35

3.3 Нумерация элементов и узлов ………. …………………….

3.4 Индексация узлов, формирование таблицы входных данных………39

ГЛАВА 4. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕМЕНТА . …. 42

4.2 Метод Лагранжа …. ………………………………………. 47

4.3 Обобщенный метод Крамера-Лагранжа …. ……………….. ………50

4.4 Свойства базисных функций ………………………………. 51

ГЛАВА 5. ВЫЧИСЛИТЕЛЬНЫЕ АСПЕКТЫ МКЭ ………………………………. 54

5.1 Общее решение краевой задачи методом Галеркина……………… 54

5.2 Матричное представление элементного вклада ………….………… 55

5.3 Формирование глобальных матриц …………………………. ………59

5.4 Стандартизация матриц элемента . ………………………. 61

5.5 Средние температуры элемента….………………………..…. 67

ГЛАВА 6. ПРОГРАММНАЯ РЕАЛИЗАЦИЯ МЕТОДА КОНЕЧНЫХ

6.1 Задание краевых условий задачи …………………………….. 69

6.2 Решение системы динамических уравнений ……………….. .72

6.3 Учет температурной зависимости свойств элемента. …. 75

6.4 Радиационный компонент теплообмена ……………………. 80

Теорией теплопередачи или теплообмена называется наука, изучающая процессы переноса тепла в пространстве с неоднородным температурным полем. Наука о теплообмене насчитывает несколько столетий, но настоящего расцвета она достигла лишь в XX веке, найдя широкое применение при решении назревших практических задач техники. Из раздела теоретической физики учение о теплообмене превратилось в самостоятельную научно-техническую дисциплину.

Особенно сложные и важные задачи стоят в области изучения теплообмена в современной авиационной, ракетной и космической технике. При сверхзвуковых скоростях полета значительно изменяются условия теплопередачи в отдельных элементах конструкции летательного аппарата, возникает необходимость его охлаждения или защиты от аэродинамического нагрева. Проблема тепловой защиты космического летательного аппарата, изучаемая в течение последних 30-40 лет, не утратила своей актуальности и сегодня, несмотря на достигнутые определенные успехи [19, 32, 36, 45-52].

Не менее важные и сложные проблемы учета теплообмена возникают при конструировании современных авиационных и ракетных двигателей. Высокая тепловая напряженность реактивных двигателей, использование криогенных топлив и многие другие важные вопросы требуют от современного конструктора этих двигателей умения произвести сложный инженерный расчет теплообмена в них и в их агрегатах.

Большое значение теория теплообмена имеет в расчетах как самих тепловых режимов летательных аппаратов, так и систем их обеспечения, а также систем жизнеобеспечения экипажа, надежной работы радиоэлектронной аппаратуры и т. д. 46.

На теории теплообмена базируются методы получения тепловой энергии, распределения, транспортирования, использования с помощью тепловых машин, аппаратов и установок, − паровых и водогрейных котлов,

теплообменников, паровых и газовых турбин, двигателей внутреннего сгорания и т. п. Анализ процессов теплообмена в теплоэнергетических и теплосиловых установках позволяет выявить их, влияние на эффективность работы этих установок и определить пути ее повышения [21-23, 35 – 38]. В современной атомной энергетике теория теплообмена используется для расчета тепловых режимов ядерных энергетических установок, проектирования систем их обеспечения и безопасности [39].

Таким образом, курс «теплопередача» является одной из важнейших теплотехнических дисциплин, необходимых для современного инженера в области авиационной, ракетной и космической техники, в теплотехнике и теплоэнергетике. Цель изучения дисциплины − подготовка студентов к усвоению теории и методов расчета теплообмена в спецкурсах и к использованию полученных знаний и навыков в профессионал ьной

деятельности и на стадии курсового и дипломного проектирования.

Проектирование теплотехнического устройства независимо от назначения последнего неотъемлемой своей частью содержит тепловое моделирование 48.

Тепловое моделирование представляет собой типичную задачу оптимального управления тепловым режимом. Главное содержание задач оптимизации в том, чтобы из различных возможных реализаций рассматриваемого процесса выбрать такую, при которой тепловой режим был бы наилучшим по некоторому заранее указанному критерию [39,42,43,42].

Выбор оптимальных тепловых режимов невозможен без методов и средств точного решения прямой задачи теплопроводности. Как правило, это требование первично [44]. Методы и средства решения ординарных задач оптимального управления и обратных задач теплопроводности необходимы, важны, оптимизируют расчеты, но требования к ним вторичны. Задачи прогноза, задачи конструктивных расчетов можно решать, лишь имея математическую модель прямой задачи теплопроводности, метод и средства ее

решения, каковым является тепловой режим теплотехнического устройства в целом или отдельных его подсистем (элементов) [45].

Под тепловым режимом традиционно понимается последовательность (во времени) температур всех частей теплотехнического устройства, необходимых для его нормального функционирования на любом этапе. Именно такое содержание понятия «тепловой режим» однозначно определяет смысл задачи обеспечения теплового режима или понимания состояния, связанного с нарушением теплового режима [32].

В инженерной практике температурные требования обычно формулируются как требования к диапазону температур, в пределах которого обеспечивается одинаковая надежность работы всех элементов устройства. Чем уже диапазон допустимых температур, тем больше весовые и энергетические затраты на обеспечение теплового режима. Поэтому так важен учет всех компонент теплообмена, приводящий к расширению диапазона температур, снижение требований к системе обеспечения режима 45.

В настоящее время все большее значение в инженерной практике теплового проектирования приобретает математическое моделирование процессов теплообмена в сложных системах. Оно позволяет заранее с помощью относительно простых средств, проверить расчетным путем правильность принятых инженерных решений и устранить возможные ошибки на стадии проектирования до изготовления системы. Сущность математического моделирования кратко можно выразить триадой «модель-алгоритм-программа». Речь идет о замене объекта его моделью и о дальнейшем исследовании на ЭВМ с помощью вычислительно — логических алгоритмов [40, 41., 42, 46, 50].

Математическая тепловая модель может быть выражена различными средствами − от языка функционального анализа и дифференциальных уравнений до вычислительного алгоритма и машинной программы.

Математическая модель должна отражать структуру и характерные особенности рассматриваемых процессов или явлений, иметь подробное формализованное математическое описание в виде системы дифференциальных уравнений и функциональных соотношений, а также моделирующий алгоритм. Математическая модель должна быть по возможности универсальной, т. е. обеспечивать расчеты и моделирование сложного нестационарного теплообмена в многоэлементных системах любой геометрической конфигурации с локально распределенными динамическими внутренними и внешними тепловыми нагрузками.

На стадиях от эскизного проектирования до экспериментальной отработки включительно одной из основных задач математического моделирования является определение действительных значений температур в характерных точках объекта и систем обеспечения теплового режима. Их соответствия требуемым значениям во всем расчетном диапазоне, изменения внутренней тепловой нагрузки и внешних воздействий при заданной структуре и параметрах разрабатываемого объекта.

Среди численных методов решения дифференциальных уравнений метод конечных элементов (МКЭ) является достаточно эффективным и универсальным [2, 3, 6].

Метод конечных элементов на сегодняшний день является общепризнанным методом структурного анализа в целом ряде областей науки и техники 4. В значительной мере это объясняется:

простой физической интерпретацией его вычислительных операций;

большой геометрической гибкость и применимость к широкому классу дифференциальных уравнений в частных производных [2, 3, 6],

обеспечением единственности получаемого решения во всех точках рассматриваемой области,

эффективностью и экономичностью при его машинной реализации в сравнении с другими методами.

Область применения МКЭ существенно расширилась, когда было показано, что возможна не только его вариационная формулировка, но и формулировка на основе метода взвешенных невязок в частности, метода Галеркина.

Универсальность метода Галеркина обеспечивается использованием непосредственно дифференциального уравнения с его краевыми условиями, описывавшего исследуемый физический процесс, и не требующий, поэтому предварительного конструирования минимизируемого затем функционала, как это делается в вариационной формулировке МКЭ. Метод Галеркина позволяет получить решение в обобщенном виде в любой системе координат для объекта любой размерности и геометрии с сохранением всех преимуществ метода конечных элементов в целом.

Данное учебное пособие посвящено изложению основ теории МКЭ применительно к краевым задачам теории поля с опорой на метод Галеркина как наиболее универсальный и точный среди других версий. Общие вопросы практической реализации метода изложены в разделах со 2-й по 6-ю главы

пособия, что позволяет использовать его в инженерной практике различных специальностей. Наибольшее внимание уделено задачам сложного теплообмена в самой общей постановке и дано их решение в общем виде − в форме алгоритма вычислительной программы.

Побудительной причиной написания пособия послужило следующее: в литературе (и не только учебного характера), посвященной численным методам решения краевых задач теории поля, подобное пособие отсутствует; в монографиях по теории и практике применения МКЭ задачи теплопроводности приводятся лишь в иллюстративных целях, причем для осесимметричных задач предложено совершенно неверное решение в [23], что показано нами в [14]. Наиболее важный для объектов авиационной и космической техники радиационный компонент теплообмена не рассматривается.

Материал пособия органически связан с изучаемыми на младших курсах дисциплинами, такими как математический анализ, векторное и тензорное исчисление, дифференциальные уравнения, численные методы анализа, теория теплообмена, программирование и применение ЭВМ. Предполагается, что студент хотя бы в общем виде знаком с целями и задачами проектирования и, в частности, теплового проектирования теплотехнических устройств, соответствующих профилю его будущей специальности [35-38, 40, 41, 47-49].

Из-за ограниченности объема в пособии: опущены некоторые специальные вопросы математического характера, относящиеся больше к теории, нежели к практике применения МКЭ; не излагается вариационная формулировка метода. Достаточно подробное освещение этих вопросов имеется в литературе 7 и при желании их можно усвоить самостоятельно, поскольку общие вопросы теории и практики применения МКЭ в пособии даны.

В отличие от традиционного подхода, в пособии рассмотрены только трехмерные (объемные) задачи сложного теплообмена, что естественно с физической точки зрения: конвективный, радиационный теплообмен и внешние поверхностные нагрузки должны учитываться на самих поверхностях элемента, а не на условных границах по его периметру, как это делается в двумерных и одномерных задачах. Такая подмена приводит к количественным несоответствиям, т.к. площади поверхностей элемента и условных границ – это не одна и та же величина, и, кроме того, нормали к ним не совпадают, что особенно скажется при учете ориентационной зависимости внешней нагрузки. Освоив изложенную в пособии методику получения решения трехмерной задачи, можно при желании найти решение задач иной размерности. Именно в этих целях в Приложении 2 дан каталог одно — и двумерных элементов.

Элементы высокого порядка – квадратичные, кубичные и т. д., а также сопутствующие им вопросы численного интегрирования в пособии не рассматриваются, ибо линейные мультиплекс-элементы обеспечивают достаточную для инженерных расчетов точность получаемого с помощью МКЭ

решения задачи сложного теплообмена. Как правило, погрешности задаваемых параметров при тепловом проектировании довольно велики, и это делает нецелесообразным поиск более точного решения.

Задачей данного пособия является практическое усвоение студентами (или специалистами теплотехнического профиля) одного из наиболее эффективных современных методов численного решения нестационарной задачи сложного теплообмена в объектах самого различного назначения и методики получения обобщенного алгоритма универсальной вычислительной программы. Изучение материала пособия должно носить последовательный характер с обязательным выполнением заданий к каждой главе. Чтение лекций следует совмещать с практическими занятиями, ориентированными на выполнение приведенных в пособии заданий. Завершать курс желательно вычислительным практикумом по расчету температурного поля элементов конкретных достаточно простых конструкций. На изучение курса, как показывает 25-ти летний опыт его преподавания, достаточно 90 часов аудиторных занятий (54 лекционных и 36 практических занятий) и примерно 36 часов для самостоятельной работы.

В настоящее время получили широкое распространение “тяжелые“ программы расчета, такие, например, как “NISA”, “ANSIS”, “SOFISTIKA” и другие, базирующиеся на конечных элементах и позволяющие численно исследовать процессы различной физической природы в многоэлементных системах и в сложных конструкциях. Освоение данного пособия позволяет осознанно использовать эти программы, особенно в части физически грамотного задания граничных условий и последующего анализа полученных результатов расчета. Пособие окажется полезным студентам как физического профиля, так и, особенно, студентам математического профиля, подходящих к решению физических задач с формальных математических позиций. Опыт преподавания показал, что математики быстрее осваивают математические аспекты “тяжелой” программы, но наполнение ее физическим смыслом вызывает у них большие трудности. В принципе, пособие следовало бы сопроводить перечнем теплофизических свойств веществ и их размерностью, но это привело бы к существенному увеличению объема пособия. Представляется достаточным дать ссылку на справочную литературу.

Опыт чтения курса показал, что последовательность изложения материала не совсем логична: во второй главе дается общее решение краевой задачи в рамках МКЭ, в то время как студенты еще не ознакомлены с другими его аспектами. Поэтому в третьем издании этот материал перенесен в 5-ю главу. В шестой главе убран пункт 6.4, посвященный частному вопросу учета конвективного компонента при течении теплоносителя по неизотермическому каналу. В остальном материал пособия сохранен практически без изменений.

Метод конечных элементов в решении задач теплопроводности Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Подгорный С. А., Меретуков З. А., Кошевой Е. П., Косачев В. С.

В работе предлагается использовать конечные элементы с функцией Хэвисайда, которые позволяют упрощать и формализовать создание кусочно-непрерывной пробной функции, используемой для решения континуальных задач методом Галеркина .

The finite element method in solving the problems of heat conduction

This work offers to supplement polynomial elements used by the step function of Heaviside and rounding functions which allows to simplify and formalizes the record of test piecewise continuous function applying it for continual problems solution by the method of Galerkin.

Текст научной работы на тему «Метод конечных элементов в решении задач теплопроводности»

Доцент С.А. Подгорный, докторант З.А. Меретуков, профессор Е.П. Кошевой, профессор B.C. Косачев

(Кубанский гос. технол. ун-т) кафедра автоматизации производственных процессов

Метод конечных элементов в решении задач теплопроводности

Ключевые слова: теплообмен, метод конечных элементов, Галеркин.

Уравнение теплопроводности [1] широко применяется для описания процесса теплопе-реноса в телах классических форм (пластина, цилиндр, сфера), на практике встречаются объекты сложной формы, и задача их описания решается методом конечных элементов [2].

В общем случае рассматривается некоторое семейство функций, определяемых конечным числом параметров. Среди таких функций нет точного решения задачи, однако подбором параметров можно попытаться при -ближенно удовлетворить уравнениям задачи и тем самым построить ее приближенное решение. Специфическим в методе конечных элементов является построение семейства функций, определяемых конечным числом параметров 6. Выберем такое семейство функций u(x) при Xmm , (х(х)Сх = -• тах ^ т’п , (5)

И над и под главной диагональю:

где к=1,2. п-1; 1=2,3. п.

Упростим задачу, полагая, что у(х) =1. В этом случае столбец свободных членов р, представляет собой величину, определяемую интегралом:

Таким образом, уравнение Ошибка! Источник ссылки не найден. принимает матричную форму:

Здесь матрица является трехдиагональной, и решение может быть получено методом Гаусса, матричным методом (умножением на обратную матрицу) или прогонки. Для систем малой размерности метод решения не существенен, но с увеличением точности решения необходимо увеличивать число конечных элементов на области существования решения, а это приводит к увеличению числа неизвестных в уравнении (1). Для определения влияния числа конечных элементов на интервале Хтт. Хтах на точность начальной аппроксимации решали систему (1) матричным методом в инженерной среде МаШСАБ при различных числах п, определяя среднее значение и(х) на этом интервале. Относительная ошибка при различном числе конечных элементов представлена ниже.

О 5 10 15 20 25 30

Рисунок 3 — Точность аппроксимации начального температурного профиля в зависимости от числа конечных элементов матричным методом

Из представленных данных видно, что 18 конечных элементах на области существо-

наибольшая точность аппроксимации началь- вания решения. При этом относительная

ного температурного профиля достигается при ошибка аппроксимации начального темпера-12

турного профиля составляет 1,5 процента. Если требуется большая точность решения, необходимо использовать метод прогонки, позволяющий решать системы большой размерности без существенных ошибок округления. Этот метод имеет существенные ограничения и применим только для систем линейных алгебраических уравнений ленточного типа. При применении метода конечных элементов ширина полосы ленточной матрицы зависит от нумерации узлов. В некоторых случаях исходная постановка задачи может оказаться настолько плохой, что даже метод конечных элементов не может помочь. В таком случае постановку задачи необходимо менять. При этом имеет место система алгебраических уравнений, в которой малые изменения коэффициентов или свободных членов приводят к значительному изменению решения. Такие системы уравнений носят название плохо обусловленных. Рассмотрим применение метода прогонки для представленной выше системы. Метод прогонки является двухшаговым. Вначале вычисляем вспомогательные величины а,, р,:

2 1 4 +«0 1 4 + а п _ 2

Эти величины используются для расчета весовых коэффициентов и,:

= ап-1 ■ ип + Рп— , и 1 = «0 • и 2 + Po, (11)

Для определения влияния числа конечных элементов на интервале Хт1П. Хтах на точность начальной аппроксимации решали систему Ошибка! Источник ссылки не найден., Ошибка! Источник ссылки не найден. и Ошибка! Источник ссылки не найден. в инженерной среде МаШСАБ при различных числах п, определяя среднее значение и(х) на этом интервале.

—*—’8. Л Л _ » 11 и о !!■!

О 5 10 15 20 25 30 35 40

Рисунок 4 — Точность аппроксимации начального температурного профиля в зависимости от числа конечных элементов методом прогонки

Относительная ошибка при различном числе конечных элементов представлена выше (Рисунок 4). Из представленных на рисунке данных видно, что метод конечных элементов позволяет снизить относительную ошибку начальной аппроксимации практически до значения менее одного процента при использовании 40 и более конечных элементов. Ис-

пользуя значения весовых коэффициентов и, как значения неизвестных временных функций и(т), можно перейти к решению краевой задачи. В этом случае пробная функция может быть представлена произведением координатных и временных функций:

^ (х )= X и, (т> Надоели баннеры? Вы всегда можете отключить рекламу.

Метод Finite Volume — реализация на примере теплопроводности

Метод Finite Volume (FVM)

В основе метода лежит разбиение области на непересекающиеся контрольные объемы(элементы), узловые точки, в которых ищется решение.Узловые точки находятся в центрах контрольных объемов.Также, как и для метода конечных разностей, для каждого элемента составляется уравнение, получается система линейных уравнений.Решая ее — находим значения
искомых переменных в узловых точках.Для отдельного элемента уравнение получается путем интегрирования исходного дифф уравнения по элементу и аппроксимации интегралов.

Термин конечный объем в статье будет часто заменятся на Элемент, будем для удобства считать их эквивалентами (элемент в данной статье не имеет ничего общего с методом конечных элементов).

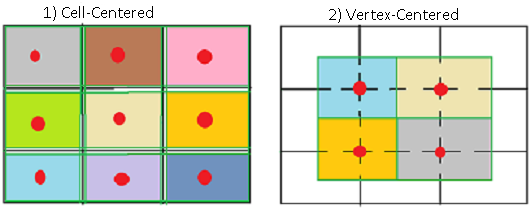
Есть 2 различных способа решения задачи по FVM:
1) грани контрольного объема совпадают с гранями элемента
2) грани контрольного объема проходят через центры граней элементов(на которые разбита область).Искомые переменные хранятся в вершинах этих элементов.Вокруг каждой вершины строится контрольный объем. Для непрямоугольной сетки этот способ имеет еще 2 подвида.

Мы будем использовать способ 1) с контрольными объемами совпадающими с элементами на которые разбита область.

Некоторые плюсы FVM:

сохранение основных величин по всей области, таких как энергия системы, масса, тепловые потоки и тд.Причом это условие выполняется даже для грубой расчетной сетки
высокая скорость расчета.Многие расчетные величины можно вычислить при разбиении области на элементы, и вычислять их на каждом шаге по времени нет необходимости.
легкость использования для задач со сложной геометрией и криволинейными границами.Легкость использования разных геометрических типов элементов — треугольники, полигоны.

Метод FVM реализуем на примере уравнения теплопроводности:

Итак основные шаги при реализации FVM:

Перевод дифф уравнения в форму пригодную для FVM — интегрирование по контрольному объему
Составление дискретного аналога, выбор способа перевода производных и других подынтегральных выражений в дискретную форму
Получение уравнения для каждого из контрольных объемов, на которые разбита область.Составление системы линейных уравнений и ее решение.

Дискретизация по времени.

Немного теории или первый шаг в реализации FVM

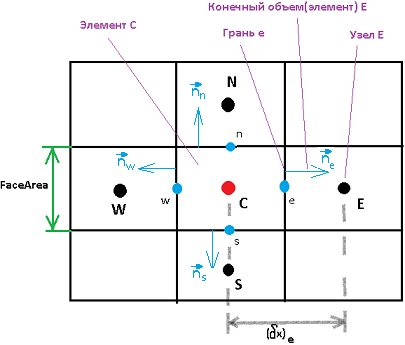
FVM на стандартной прямоугольной сетке

На рисунке изображен Элемент С и его соседние элементы справа(E), слева(W), сверху(N) и снизу(S).У элемента С есть 4 грани обозначенные буквами e w n s.Именно эти 4 грани и составляют периметр элемента и по ним производится интегрирование.Для каждого элемента в результате получаем дискретный аналог исходного дифф уравнения.

Составим дискретный аналог для элемента С.Для начала нужно разобраться с интегралом (3).Интеграл это ведь по факту сумма.Поэтому мы и заменяем интеграл по всей поверхности элемента, на сумму по 4-м составляющим этой поверхности, тоесть 4 граням элемента.

Уравнение (7) и есть конечное уравнение для элемента С, из него мы на каждом шаге по времени получаем новое значение температуры (Tnew) в элементе С.

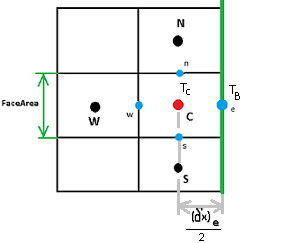
Граничные условия на прямоугольной сетке

Мы рассмотрим только 2 вида граничных условий.

Задана температура Tb на границе
Задан поток FluxB на границе, рассмотрим только случай когда FluxB=0, т.е. грань e будет теплоизолирована(Insulated)

Случай 2) самый простой, поскольку получается что грань e не потребуется при дискретизации(т.к. все коэффициенты Flux=0) и можно ее просто пропустить.

Теперь рассмотрим случай 1).Дискретизация грани e будет в целом похожа на ту что уже была описана.Будут только 2 изменения — вместо Te будет известное граничное значение Tb и вместо расстояния DXe будет DXe/2.В остальном можно рассматривать значение Te так, как будто это был бы обычный соседний узел E.Теперь подробнее распишем терм для граничного элемента С.

Пример численных расчетов на прямоугольной сетке

FVM в задачах со сложной геометрией

Здесь как раз проявляется преимущество FVM, где также, как и в методе конечных элементов, можно представлять область с круглыми границами через разбиение на треугольники или любые другие полигоны.Но FVM имеет еще 1 плюс — при переходе от треугольников к полигонам с большим числом сторон не требуется абсолютно ничего менять, конечно если код был написан для произвольного треугольника а не равностороннего.Более того, можно без изменения кода использовать смесь разных элементов — треугольники, полигоны, квадраты и тд.

Рассмотрим общий случай, когда вектор соединяющий центры 2-х элементов не совпадает с вектором нормали к общей грани этих элементов.Вычисление потока flux через грань теперь будет состоять из 2-х частей.В первой будет расcчитываться ортогональная составляющая а во второй так называемая «кросс-диффузия».

На картинке изображены 2 элемента, С — текущий рассматриваемый элемент и F — соседний элемент.Опишем дискретизацию для грани, разделяющей эти 2 элемента.Вектор соединяющий центры элементов — DCF.Вектор e — это единичный вектор по направлению DCF.Вектор Sf — направлен по нормали к грани, его длинна равна длине грани.

В исходниках я не стал реализовывать терм с кроссдиффузией, т.к встал вопрос — как проверить корректность такой реализации.Визуально сравнение результатов Матлаб и моих ничем не отличалось в отсутствии кросс-диффузии.Видимо это связано с тем что Матлаб любит треугольники близкие к равносторонним, что в итоге делает кроссдиффузию=0.Возможно позже еще вернусь к этому вопросу.

Расчет граничных элементов ничем не отличается от расчетов не на границе, вместо центра соседнего элемента берется центр грани, ну и как обычно подставляется температура на границе.
В моей реализации в итоге получается так:

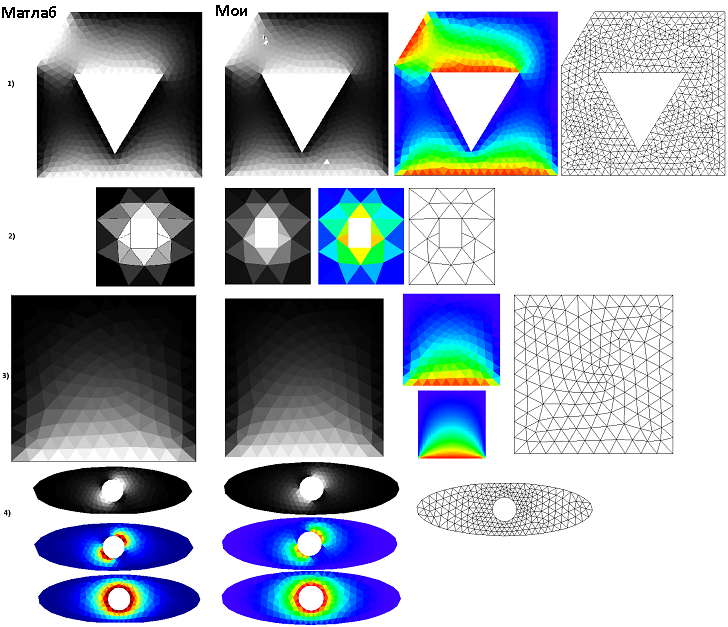
Примеры и проверка результатов

Описание структуры исходников

Гитхаб с исходниками лежит тут
Основная версия в папке heat2PolyV2.То что относится к вычислительной части лежит в heat2PolyV2\Src\FiniteVolume\.

Вначале файла Scene2.cs — параметры которые можно менять для отображения в разных цветовых схемах, масштаб, отображение mesh и т.д.Сами примеры хранятся в heat2PolyV2\bin\Debug\Demos\
Выгрузку из Матлаба сделать просто — нужно открыть pde toolbox, открыть m файл (либо создать самому с нуля), зайти в меню Mesh-Экспорт mesh, нажать ОК; перейти в основной Матлаб, в панельке появятся переменные — матрицы p e t, открыть файл savemymesh.m, выполнить его, появится файл p.out, перенести его в папку Demos.
В исходниках для выбора примера необходимо задать имя файла в строке param.file = «p»;(FormParam.cs).Далее необходимо применить граничные условия — для готовых примеров можно просто раскомментировать соответствующие блоки в MainSolver.cs:

Смысл тут простой — Матлаб разделяет границы по доменам, например внешние и внутренние.Также для каждого домена границы разбиты на части (группы), чтобы можно было задавать условия на участках границы по отдельности — например справа или снизу.
Возможно и вовсе не использовать Матлаб, а вручную прописать все элементы(треугольники) и их вершины + грани(только для граничных элементов)

источники:

http://cyberleninka.ru/article/n/metod-konechnyh-elementov-v-reshenii-zadach-teploprovodnosti

http://habr.com/ru/post/276193/