Метод конечных объемов для двумерного уравнения теплопроводности

Двумерное уравнение теплопроводности. Фролова Ксения. 6 курс

Содержание

Постановка задачи [ править ]

Необходимо решить задачу Коши для двумерного уравнения теплопроводности (дифференциальное уравнение в частных производных второго порядка, которое описывает распределение температуры в заданной области пространства и его изменение во времени.) с использованием средств параллельного программирования на основе MPI. Задача решается для однородного уравнения теплопроводности (система теплоизолирована) в области [0..L]x[0..L]:
[math]\frac<\partial U> <\partial t>— a^2(\frac<\partial^2 U><\partial x^2>+\frac<\partial^2 U><\partial y^2>) = 0[/math]
[math]U(t=0) = U_0[/math]
при граничных условиях:
[math] U(x,y,t) = \beginT_0, x=0\\ T_1, x!=0 \end[/math]
Используемые величины параметров:
[math]L=1, T_0=100, T_1=0[/math]

Используемый метод [ править ]

В вычислительных системах с распределенной памятью процессоры работают независимо друг от друга. Для организации параллельных вычислений в таких условиях необходимо иметь возможность распределять вычислительную нагрузку и организовать информационное взаимодействие (передачу данных) между процессорами. Параллельное программирование служит для создания программ, эффективно использующих вычислительные ресурсы за счет одновременного исполнения кода на нескольких вычислительных узлах. Для создания параллельных приложений используются параллельные языки программирования и специализированные системы поддержки параллельного программирования, такие как MPI и OpenMP. Итак, MPI — это библиотека передачи сообщений, собрание функций на C/C++ (или подпрограмм в Фортране), облегчающих коммуникацию (обмен данными и синхронизацию задач) между процессами параллельной программы с распределенной памятью. Акроним MPI установлен для Message Passing Interface (интерфейс передачи сообщений). Под параллельной программой в рамках MPI понимается множество одновременно выполняемых процессов. Все процессы порождаются один раз, образуя параллельную часть программы. Каждый процесс работает в своем адресном пространстве, никаких общих переменных или данных в MPI нет. Процессы могут выполняться на разных процессорах, но на одном процессоре могут располагаться и несколько процессов (в этом случае их исполнение осуществляется в режиме разделения времени).

Реализация [ править ]

При решении поставленной задачи будем использовать замену частных производных в дифференциальных уравнениях их разностными аналогами. Сеточный метод, основанный на замене в дифференциальном уравнении производных конечными разностями, называют методом конечных разностей, а сеточную схему такого метода — конечно-разностной.
По аналогии с одномерной задачей для уравнения теплопроводности вводим явную конечно-разностную схему. Область [0..L]x[0..L] разбивается на подобласти согласно количеству процессов в выполняемой параллельной программе. На каждом полученном таким способом интервале процесс интегрирования осуществляется отдельным процессом, при этом в связи с использованием явной схемы соседние процессы должны обмениваться крайними значениями, полученными на предыдущем шаге, для выполнения следующего шага.
Программа для решения двумерного уравнения теплопроводности: программа

Результаты [ править ]

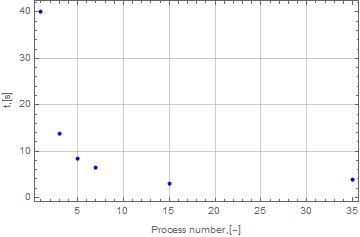
Найдено решение однородного уравнения теплопроводности в двумерной постановке для следующей сетки узлов: 300х300.

Показано, что при увеличении количества процессов уменьшается время расчета. Также из приведенного графика видно, что для малого числа узлов в сетке использование большого количества процессов не обосновано — выигрыш во времени либо незначителен, либо же затраченное время увеличивается.

Метод Finite Volume — реализация на примере теплопроводности

Метод Finite Volume (FVM)

В основе метода лежит разбиение области на непересекающиеся контрольные объемы(элементы), узловые точки, в которых ищется решение.Узловые точки находятся в центрах контрольных объемов.Также, как и для метода конечных разностей, для каждого элемента составляется уравнение, получается система линейных уравнений.Решая ее — находим значения
искомых переменных в узловых точках.Для отдельного элемента уравнение получается путем интегрирования исходного дифф уравнения по элементу и аппроксимации интегралов.

Термин конечный объем в статье будет часто заменятся на Элемент, будем для удобства считать их эквивалентами (элемент в данной статье не имеет ничего общего с методом конечных элементов).

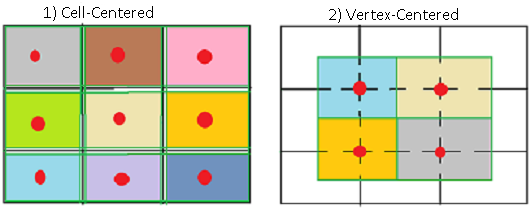
Есть 2 различных способа решения задачи по FVM:
1) грани контрольного объема совпадают с гранями элемента
2) грани контрольного объема проходят через центры граней элементов(на которые разбита область).Искомые переменные хранятся в вершинах этих элементов.Вокруг каждой вершины строится контрольный объем. Для непрямоугольной сетки этот способ имеет еще 2 подвида.

Мы будем использовать способ 1) с контрольными объемами совпадающими с элементами на которые разбита область.

Некоторые плюсы FVM:

• сохранение основных величин по всей области, таких как энергия системы, масса, тепловые потоки и тд.Причом это условие выполняется даже для грубой расчетной сетки
• высокая скорость расчета.Многие расчетные величины можно вычислить при разбиении области на элементы, и вычислять их на каждом шаге по времени нет необходимости.
• легкость использования для задач со сложной геометрией и криволинейными границами.Легкость использования разных геометрических типов элементов — треугольники, полигоны.

Метод FVM реализуем на примере уравнения теплопроводности:

Итак основные шаги при реализации FVM:

1. Перевод дифф уравнения в форму пригодную для FVM — интегрирование по контрольному объему
2. Составление дискретного аналога, выбор способа перевода производных и других подынтегральных выражений в дискретную форму
3. Получение уравнения для каждого из контрольных объемов, на которые разбита область.Составление системы линейных уравнений и ее решение.

Дискретизация по времени.

Немного теории или первый шаг в реализации FVM

FVM на стандартной прямоугольной сетке

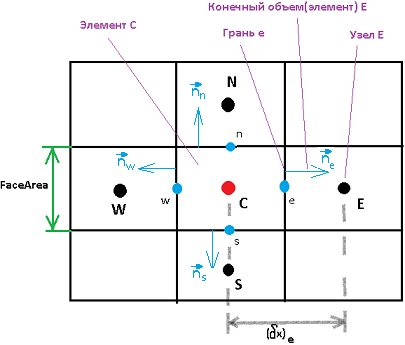
На рисунке изображен Элемент С и его соседние элементы справа(E), слева(W), сверху(N) и снизу(S).У элемента С есть 4 грани обозначенные буквами e w n s.Именно эти 4 грани и составляют периметр элемента и по ним производится интегрирование.Для каждого элемента в результате получаем дискретный аналог исходного дифф уравнения.

Составим дискретный аналог для элемента С.Для начала нужно разобраться с интегралом (3).Интеграл это ведь по факту сумма.Поэтому мы и заменяем интеграл по всей поверхности элемента, на сумму по 4-м составляющим этой поверхности, тоесть 4 граням элемента.

Уравнение (7) и есть конечное уравнение для элемента С, из него мы на каждом шаге по времени получаем новое значение температуры (Tnew) в элементе С.

Граничные условия на прямоугольной сетке

Мы рассмотрим только 2 вида граничных условий.

1. Задана температура Tb на границе
2. Задан поток FluxB на границе, рассмотрим только случай когда FluxB=0, т.е. грань e будет теплоизолирована(Insulated)

Случай 2) самый простой, поскольку получается что грань e не потребуется при дискретизации(т.к. все коэффициенты Flux=0) и можно ее просто пропустить.

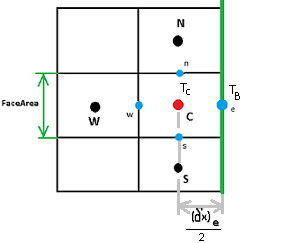
Теперь рассмотрим случай 1).Дискретизация грани e будет в целом похожа на ту что уже была описана.Будут только 2 изменения — вместо Te будет известное граничное значение Tb и вместо расстояния DXe будет DXe/2.В остальном можно рассматривать значение Te так, как будто это был бы обычный соседний узел E.Теперь подробнее распишем терм для граничного элемента С.

Пример численных расчетов на прямоугольной сетке

FVM в задачах со сложной геометрией

Здесь как раз проявляется преимущество FVM, где также, как и в методе конечных элементов, можно представлять область с круглыми границами через разбиение на треугольники или любые другие полигоны.Но FVM имеет еще 1 плюс — при переходе от треугольников к полигонам с большим числом сторон не требуется абсолютно ничего менять, конечно если код был написан для произвольного треугольника а не равностороннего.Более того, можно без изменения кода использовать смесь разных элементов — треугольники, полигоны, квадраты и тд.

Рассмотрим общий случай, когда вектор соединяющий центры 2-х элементов не совпадает с вектором нормали к общей грани этих элементов.Вычисление потока flux через грань теперь будет состоять из 2-х частей.В первой будет расcчитываться ортогональная составляющая а во второй так называемая «кросс-диффузия».

На картинке изображены 2 элемента, С — текущий рассматриваемый элемент и F — соседний элемент.Опишем дискретизацию для грани, разделяющей эти 2 элемента.Вектор соединяющий центры элементов — DCF.Вектор e — это единичный вектор по направлению DCF.Вектор Sf — направлен по нормали к грани, его длинна равна длине грани.

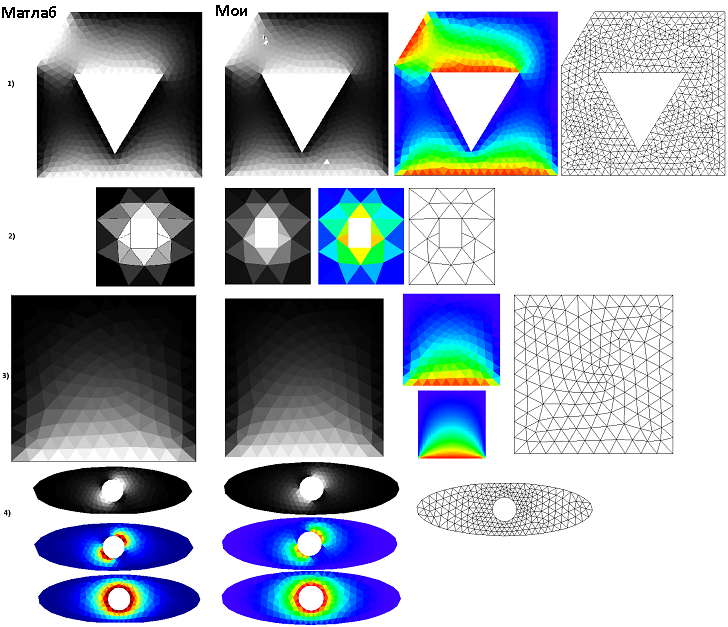
В исходниках я не стал реализовывать терм с кроссдиффузией, т.к встал вопрос — как проверить корректность такой реализации.Визуально сравнение результатов Матлаб и моих ничем не отличалось в отсутствии кросс-диффузии.Видимо это связано с тем что Матлаб любит треугольники близкие к равносторонним, что в итоге делает кроссдиффузию=0.Возможно позже еще вернусь к этому вопросу.

Расчет граничных элементов ничем не отличается от расчетов не на границе, вместо центра соседнего элемента берется центр грани, ну и как обычно подставляется температура на границе.
В моей реализации в итоге получается так:

Примеры и проверка результатов

Описание структуры исходников

Гитхаб с исходниками лежит тут
Основная версия в папке heat2PolyV2.То что относится к вычислительной части лежит в heat2PolyV2\Src\FiniteVolume\.

Вначале файла Scene2.cs — параметры которые можно менять для отображения в разных цветовых схемах, масштаб, отображение mesh и т.д.Сами примеры хранятся в heat2PolyV2\bin\Debug\Demos\
Выгрузку из Матлаба сделать просто — нужно открыть pde toolbox, открыть m файл (либо создать самому с нуля), зайти в меню Mesh-Экспорт mesh, нажать ОК; перейти в основной Матлаб, в панельке появятся переменные — матрицы p e t, открыть файл savemymesh.m, выполнить его, появится файл p.out, перенести его в папку Demos.
В исходниках для выбора примера необходимо задать имя файла в строке param.file = «p»;(FormParam.cs).Далее необходимо применить граничные условия — для готовых примеров можно просто раскомментировать соответствующие блоки в MainSolver.cs:

Смысл тут простой — Матлаб разделяет границы по доменам, например внешние и внутренние.Также для каждого домена границы разбиты на части (группы), чтобы можно было задавать условия на участках границы по отдельности — например справа или снизу.
Возможно и вовсе не использовать Матлаб, а вручную прописать все элементы(треугольники) и их вершины + грани(только для граничных элементов)

Метод конечных объемов для двумерного уравнения теплопроводности

Методические указания к лабораторным работам

по математическому моделированию

Составитель Е.А. Маслов

Томск – 2008 Численное решение двумерных нестационарных уравнений теплопроводности: методические указания к лабораторным работам по математическому моделированию / Сост.

Е.А. Маслов, Томск: Изд-во Том. гос. архит.-строит. ун-та, 2007. – 29 с.

Рецензент доцент Томского государственного университета, к.ф.-м.н. И.К. Жарова Редактор Е.Ю. Глотова Методические указания для выполнения лабораторных работ по курсу “Математическое моделирование плазмохимических процессов” предназначены студентам специальности 270113 – “Механизация и автоматизация строительства”, обучающимся по специализации “Плазменные технологии в строительной индустрии“.

Печатаются по решению методического семинара кафедры прикладной механики и материаловедения, протокол № 82 от 04. 12. 2007г.

Утверждены и введены в действие проректором по учебной работе В.В. Дзюбо с 01.01. до 01.10. Подписано в печать Формат 60х90/16.

Бумага офсет. Гарнитура Таймс, печать офсет.

Уч.-изд.л. 1,5. Тираж 100 экз. Заказ № Изд-во ТГАСУ, 634003, г. Томск, пл. Соляная, 2.

Отпечатано с оригинал-макета в ООП ТГАСУ.

634003, г. Томск, ул. Партизанская, 15.

Оглавление 1. Общие сведения

2. Метод конечных разностей (МКР)

3. Линейные задачи теплопроводности

3.1. Двумерное уравнение теплопроводности

3.2. Алгоритм численного решения (метод «расщепления по пространственным координатам»)

3.3. Решение систем линейных алгебраических уравнений методом прогонки

3.4. Листинг программы решения рассматриваемой задачи (язык программирования Fortran Powerstation). 3.5. Cписок основных идентификаторов

3.6. Тестовая задача

4. Варианты заданий

Список рекомендуемой литературы

1. ОБЩИЕ СВЕДЕНИЯ Теплопередача, или теплообмен – это учение о самопроизвольных необратимых процессах распределения (переноса) теплоты в пространстве с неоднородным полем температуры [1].

При проектировании различных теплосиловых установок: тепловых двигателей, компрессоров, холодильных машин, летательных аппаратов, технологического оборудования, особенно химической и пищевой промышленности, и ряда других устройств – следует учитывать процессы переноса теплоты; часто эти процессы становятся определяющими при выборе конструкций, в которых осуществляется оптимальный тепловой режим [1].

Для того, чтобы конструкция работала надежно, необходимо предусмотреть меры, которые установили бы предел росту температуры. В противном случае нормальная работа таких установок может прекратиться, так как конструкционные материалы при нагревании теряют прочность и при определенной температуре разрушаются. Например, если не предусмотреть специальных мер для защиты камеры сгорания и сопла, то ракетный двигатель разрушится в течение долей секунды. Баллистическая ракета, входящая в плотные слои атмосферы, без тепловой защиты ее головной части и стенок корпуса разрушится в течение нескольких секунд, так как температура ее головной части при этом достигает нескольких тысяч градусов [1].

При работе компактных электронных устройств генерируется теплота, которая может повысить температуру отдельных элементов до уровня, при котором устройство не будет выполнять своих функций [1].

Сложный процесс переноса теплоты разбивают на ряд более простых: теплопроводность, конвекция и теплообмен излучением. Различают молекулярный и конвективный механизмы переноса теплоты.

Молекулярный перенос теплоты осуществляется посредством теплового движения микрочастиц в среде с неоднородным распределением температуры [1].

Конвективный перенос теплоты осуществляется в среде с неоднородным распределением скорости и температуры макроскопическими элементами среды при их перемещении.

Теплопроводностью называют молекулярный перенос теплоты в сплошной среде, обусловленный наличием градиента температуры (закон Фурье) [1].

Конвективным теплообменом называют процесс, обусловленный совместным действием конвективного и молекулярного переноса теплоты. В инженерной практике большое значение имеет частный случай этого способа переноса теплоты, а именно: теплоотдача – конвективный теплообмен между движущейся средой и поверхностью ее раздела с другой средой: твердым телом, жидкостью или газом [1].

Теплообмен излучением – это процесс, который происходит следующим образом: внутренняя энергия вещества превращается в энергию излучения (энергия фотонов или электромагнитных волн, излучаемых телом или средой), далее происходит распространение излучения в пространстве (процесс переноса излучения), далее энергия излучения поглощается веществом, которое оказалось на пути фотонов или электромагнитных волн [1].

Нестационарный перенос тепла теплопроводностью описывается следующим уравнением, записанным в декартовой системе координат:

Это уравнение устанавливает связь между временным и пространственным изменением температуры в любой точке тела. Здесь – плотность (кг/м3), с – удельная теплоемкость (Дж/(кг·С)), – коэффициент теплопроводности (Вт/(м·С)), T – температура (С), x, y – декартовы координаты (м), t – время (с), Q w (x, y, t, T) – мощность внутренних источников тепловыделения (Вт/м3).

Уравнение (1) описывает множество вариантов развития процесса кондуктивного теплопереноса (теплопроводности).

Чтобы из большого количества этих вариантов выбрать один и дать его полное математическое описание, к соотношению (1) необходимо добавить условия однозначности, которые содержат геометрические, физические, начальные и граничные условия.

Геометрические условия определяют форму и размеры тела, в котором протекает изучаемый процесс. Физические условия определяют теплофизические характеристики тела,, с. Временные (начальные) условия содержат распределение температуры в теле в начальный момент времени:

При равномерном распределении температуры в теле начальное условие упрощается: t=0: Т=Т0=const. Граничные условия определяют особенности протекания процесса на поверхности тела и могут быть заданы несколькими способами.

1. Граничные условия первого рода – задается распределение температуры на поверхности (или границе) тела для каждого момента времен [1]:

где T W – температура на поверхности тела. Во многих практически значимых вариантах T W = const.

2. Граничные условия второго рода – задается значение теплового потока для каждой точки поверхности (или границы) тела в любой момент времени (закон Фурье) [1]:

где n – нормаль к поверхности тела, q w – тепловой поток (Вт/м2). Наиболее часто используется условие q w = const.

3. Граничные условия третьего рода – задается взаимосвязь между потоком тепла за счет теплопроводности от твердой стенки и тепловым потоком из окружающей среды за счет температурного напора (закон Ньютона – Рихмана) [1]:

где – коэффициент теплообмена (Вт/(м2·С)), T e – температура окружающей среды вблизи поверхности тела.

4. Граничные условия четвертого рода – для определения теплового взаимодействия между элементами, имеющими различные теплофизические характеристики, задают условия равенства температур и тепловых потоков по обе стороны от границы раздела [1]:

где x Г, y Г – координаты границы раздела сред; Т 1, Т 2 – температуры соприкасающихся сред. Это условие применяется, например, при решении задач теплопроводности для многослойных пластин.

Дифференциальное уравнение (1) вместе с условиями однозначности дает полную математическую формулировку краевой задачи теплопроводности.

2. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ (МКР) Сформулированное уравнение (1) с соответствующими краевыми условиями (начальными и граничными) будем решать численно, т.е. воспользуемся возможностями ЭВМ.

Численным решением называется решение, полученное в виде таблицы чисел [2].

При решении дифференциального уравнения в частных производных наиболее часто используется метод конечных разностей (МКР). Идея МКР решения краевых задач весьма проста и видна уже из самого названия: вместо производных в дифференциальном уравнении используются их конечноразностные аппроксимации. При построении дискретных аппроксимаций краевых дифференциальных задач нужно стремиться увязать две, возможно, противоречивые цели: хорошее качество аппроксимации и эффективное устойчивое решение получающихся при этом алгебраических систем [2].

При использовании МКР для задач теплопроводности твердое тело представляют в виде совокупности узлов. Аппроксимируя (заменяя) частные производные дифференциального уравнения (1) конечными разностями, получают систему линейных алгебраических уравнений для определения температуры как локальной характеристики в каждом узле сетки. Полученная система является незамкнутой, для ее замыкания используют разностное представление граничных условий. В результате получают замкнутую систему линейных алгебраических уравнений, которую решают численными методами с помощью ЭВМ [2].

3. ЛИНЕЙНЫЕ ЗАДАЧИ ТЕПЛОПРОВОДНОСТИ

3.1. Двумерное уравнение теплопроводности В качестве примера применения метода конечных разностей рассмотрим задачу на основе двумерного нестационарного уравнения теплопроводности. Анализируется задача теплообмена между высокотемпературной струей и пластиной из конструкционного материала (КМ), внешняя поверхность которого подвергается воздействию высокотемпературной высокоскоростной одно- или двухфазной струи с заданными параметрами.

Схема взаимодействия высокотемпературной струи с преградой представлена на рис. 1.

Рис. 1. Область решения задачи: x, y –декартовы координаты;

L x – ширина пластины; L y – толщина пластины; l g – протяженность области воздействия струи; Q g – высокотемпературный поток; A, B, При постановке задачи были приняты следующие допущения:

1. Вклад радиационной составляющей в теплообмен на внешней поверхности не учитывается.

2. Возможные процессы плавления и окисления материала преграды активными компонентами газового потока не рассматриваются.

3. Влияние конденсированной фазы в струе на теплообмен учитывается через коэффициент теплообмена g на разрушающейся поверхности.

4. Теплофизические характеристики (,, с) КМ постоянны.

Математическая модель, описывающая в рамках сформулированной задачи процесс прогрева КМ, включает нестационарное двумерное уравнение теплопроводности (2) с соответствующими начальными (3) и граничными условиями (4) – (8):

– условие (II род) симметрии на оси 0Y (AB):

– условие (III род) кондуктивно-конвективного теплообмена газового потока с поверхностью КМ (BC):

– условие (III род) кондуктивно-конвективного теплообмена с воздухом на нагреваемой поверхности (CD):

– условие (III род) кондуктивно-конвективного теплообмена с воздухом на боковой поверхности (DE):

– условие (III род) кондуктивно-конвективного теплообмена с воздухом на тыльной стороне пластины (AE):

где T – температура; t – время; – плотность; с – коэффициент удельной теплоемкости; – коэффициент теплопроводности; – коэффициент теплообмена. Индексы «g», «e» и «s» относятся к характеристикам струи, окружающей среды и материала пластины соответственно.

3.2. Алгоритм численного решения (метод «расщепления по пространственным координатам») Для численного решения задачи (2) – (8) воспользуемся методом Писмена – Рекфорда (метод расщепления по пространственным координатам) [2, 3]. Для аппроксимации дифференциального уравнения (2) разностным методом введем пространственно–временную сетку с координатами x i = i·h x ;

y j = j·h y, t k = k·, где h x, h y – шаги по пространству, – шаг по времени; i 0, N x, j 0, N y и k 0, K. Таким образом, вся расчетная область покрывается сеткой (рис. 2) [2].

Введем следующее обозначение: T ( xi, y j, t k ) Ti,kj. Дискретизацию уравнения (2) будем проводить на основе локально-одномерной схемы А.А. Самарского, которая является абсолютно устойчивой и обладает свойством суммарной аппроксимации. Суть этого подхода состоит в том, что шаг по времени реализуется в два этапа – на промежуточном (полушаге /2) временном шаге проводим дискретизацию двумерного уравнения (2) только в направлении оси х и получаем одномерное уравнение, после его решения проводим вновь дискретизацию уравнения (2), но уже в направлении оси у и, решая полученное одномерное уравнение, определяем поле температуры на целом шаге по времени. Представим (2) в разностном виде, используя неявную схему на каждом полушаге по времени [3]:

Аппроксимация граничных условий (3) – (8):

Разностные уравнения (9), (10) сводятся к стандартному трехдиагональному виду и решаются последовательно методом прогонки [4]. Сначала для всей области решается уравнение (9), после того, как его решение будет найдено, переходят к решению уравнения (10).

3.3. Решение систем линейных алгебраических уравнений Рассмотрим решение уравнения (9) методом прогонки.

Приведем это уравнение к виду [4]:

Преобразуем уравнение (9):

Тогда Для границ (АВ) и (СD) (см. рис. 2) для точек 0 и N x мы должны записать выражение (16) в виде:

Так как граничные точки имеют только по одной соседней точке, то выражения (18) и (19) могут рассматриваться в виде (16), если положить c 0 = 0 для (18) и b N = 0 для (19).

Для реализации граничных условий (11) и (14) на соответствующих границах мы должны положить коэффициенты a 0, b 0, d 0, a N, c N, d N, входящие в (18), (19), следующие:

Алгоритм прогонки начинается с записи уравнения (18) в виде:

где Соотношение (21) подставляется в (16) для i = 0. В результате получается, что T0k, 1 / 2 выражается через T1,kj1 / 2. Проj должая процесс последовательной подстановки (или прямой прогонки), можно выразить Ti,kj1 / 2 через Ti1,1j/ 2 :

где P i и Q i – новые коэффициенты, появившиеся в процессе подстановки.

Представим, что мы находимся на стадии процесса подk становок, когда только что выразили Ti1,1j/ 2 в виде Если подставить (24) в (16), то получается выражение которое может быть переписано в форме (23). Таким образом, можно получить формулы для P i и Q i :

Заметим, что знаменатели в выражениях (26) и (26а) одинаковые.

Выражения (26) и (26а) рекурсивные, т.е. P i и Q i зависят от значений P i-1 и Q i-1. Такой рекурсивный процесс нуждается в отправной точке. Она обеспечивается выражениями (22), которые не рекурсивны [4].

Перейдя к вычислению P N и Q N, можно обнаружить, что, как b N = 0, P N тоже будет равно нулю (см. (20) и (26)). В результате согласно (17) T N будет равно Q N. Рассчитав таким образом значение T N, можно начать процесс обратной прогонки с использованием формулы (24) для получения Итоговый алгоритм решения [4].

Алгоритм прогонки может быть разбит на следующие шаги [4].

1. Вычисляем P 0 и Q 0 по выражениям (22).

2. Получаем P i и Q i для i = 1, 2. N, используя рекурсивные выражения (26) и (26а).

4. Подставляем найденные значения величин в формулу (24) для i = N–1, N–2. 0 и определяем T N–1, T N–2, T N–3. T 2, T1 и T0.

Алгоритм решения уравнения (10) аналогичен. Отличие составляют записи граничных условий на границах (ВС), (СD) и (AE). То есть запись коэффициентов a 0, b 0, d 0, a N, c N, d N, входящих в (18), (19), которые будут следующими:

Коэффициенты a i, b i, c i, d i уравнения (10), входящие в (16), примут следующий вид:

Прогонка будет осуществляться по индексу j, не известные будут Ti,kj1, Ti,kj11 и Ti,kj11.

3.4. Листинг программы решения рассматриваемой задачи (язык программирования Fortran Powerstation) Program Tempreture_Dim Integer Nx,Ny,K Real*8 Lx, Ly, lg, Ros, Cps, Lams, Alfae, Alfag, T0, Parameter (Lx=0.1, Ly=0.15, lg=0.05, Nx=100, Real*8 a0, b0, d0, an, cn, dn Real*8 TXY(0:Nx, 0:Ny) Real*8 TX(0:Nx), TY1(1:Nx–1) Real*8 TY(0:Ny), TX1(1:Ny–1) Real*8 Axi(0:Nx), Bxi(0:Nx), Cxi(0:Nx), Dxi(0:Nx) Real*8 Ayj(0:Ny), Byj(0:Ny), Cyj(0:Ny), Dyj(0:Ny) Open(1,file=’T(x,y).txt’) Open(2,file=’T(0,y).txt’) Nxlg = int (lg / hx) !кол-во точек на гр. (ВС) Do j = 1, Ny–1 !направление 0X !гр. усл.(II рода) левая гр.(AB) ao To = bo T1+do !г.у.(III рода) правая гр.(DE) an Tn = cn Tn–1+dn TY1(1:Nx–1) = TXY(1:Nx–1,j) !Ti,j call ABCD_X(Nx, Axi, Bxi, Cxi, Dxi, Lams, Ros, call TDMA(Nx, Axi, Bxi, Cxi, Dxi, TX) TXY(0:Nx, j) = TX(0:Nx) TXY(0:Nx, 0) = TXY(0:Nx, 1) TXY(0:Nx, Ny) = TXY(0:Nx, Ny–1) Do i = 1, Nx–1 !направление 0Y !г.у.(III рода)на нижней г. (AE)ao To=bo T1+do !г.у.(III рода)на г.(BC)и(AD) an Tn=cn Tn–1+dn TX1(1:Ny–1) = TXY(i,1:Ny–1) !Ti,1:Ny– call ABCD_Y(Ny, Ayj, Byj, Cyj, Dyj, Lams, Ros, Cps, call TDMA(Ny, Ayj, Byj, Cyj, Dyj, TY) TXY(i, 0:Ny) = TY(0:Ny) TXY(0, 0:Ny) = TXY(1, 0:Ny) TXY(Nx, 0:Ny) = TXY(Nx–1, 0:Ny) write(*, ‘(A, f5.2, A)’) ‘ Time= ‘, L*tau, ‘.c’ write(1, ‘(101e10.3)’ ) Txy(0:Nx, j) write(2, ‘(e10.3, A, e10.3)’ ) j*hy, ‘ ‘, Txy(0, j) end do close(1) close(2) !процедура трехточечной прогонки Subroutine TDMA(N, a, b, c, d, T) integer n real*8 A(0:n), B(0:n), C(0:n), D(0:n), T(0:n) real*8 P(0:n), Q(0:n) P(0) = b(0) / a(0) Q(0) = d(0) / a(0) P(i) = b(i) / (a(i) – c(i) * P(i–1)) Q(i) = (d(i) + c(i) * Q(i–1)) / (a(i) – c(i) * P(i–1)) end do T(n) = Q(n) do i = N–1, 0, – T(i) = P(i) * T(i+1) + Q(i) end do !прогоночные коэффициенты по оси OX Subroutine ABCD_X(Nx, Axi, Bxi, Cxi, Dxi, Lams, Ros, integer Nx real*8 Lams, Ros, Cps, hx, tau real*8 Axi(0:Nx), Bxi(0:Nx), Cxi(0:Nx), Dxi(0:Nx), real*8 a0, b0, d0, an, cn, dn !г.у. для левой границы ao To = bo T1+do !г.у. для правой границы an Tn = cn Tn–1+dn Axi(Nx) = an Cxi(Nx) = cn Dxi(Nx) = dn Axi(i) = 2. * (Cps * Ros / tau + Lams / hx**2) Bxi(i) = Lams / hx** Cxi(i) = Lams / hx** Dxi(i) = 2. * Cps * Ros * TY1(i) / tau !прогоночные коэффициенты по оси OY Subroutine ABCD_Y(Ny, Ayj, Byj, Cyj, Dyj, Lams, Ros, integer Ny real*8 Lams, Ros, Cps, hy, tau real*8 Ayj(0:Ny), Byj(0:Ny), Cyj(0:Ny), Dyj(0:Ny), real*8 a0, b0, d0, an, cn, dn !г.у. для нижней границы ao To = bo T1+do !г.у. для верхней границы an Tn = cn Tn–1+dn Ayj(j) = 2. * (Cps * Ros / tau + Lams / hy**2) 3.5. Cписок основных идентификаторов Nx, Ny – количество узлов по оси Х и У соответственно;

K – количество шагов интегрирования по времени;

Lx, Ly – ширина и толщина пластины соответственно (м);

lg – протяженность области воздействия струи (м);

Ros – плотность материала пластины (кг/м3);

Cps – теплоемкость материала пластины (Дж/(кг·К));

Lams – теплопроводность материала пластины (Вт/(м·К));

Alfae – коэффициент теплообмена материала пластины с окружающей средой «воздух» (Вт/(м2·К));

Alfag – коэффициент теплообмена материала пластины с плазменной струей (Вт/(м2К));

Т0 – начальная температура материала пластины (К);

Tg –температура плазменной струи (К);

Te – температура окружающей среды «воздух» (К);

Time – время протекающего процесса.

Результаты вычисления по приведенной программе в 3.4. при следующих значениях геометрических и режимных параметрах: L x = 0,1 м, L y = 0,15 м, l g =0,05 м, s = 1800 кг/м3;

e = 30 Вт/(м2·°С). Результаты процесса нагрева пластины через 60 секунд приведены на рисунках 3, 4.

Рис. 3. Распределение температуры по толщине пластины в направлении оси 0Y 1. Пластина толщиной 0,2 м из огнеупорного материала Бакор–33 (ГОСТ 23053–78) находилась при постоянной температуре T 0 = 20 С. В начальный момент времени t = 0 с одной стороны пластины появился источник тепла с постоянной температурой T 1 = 1400 С, с другой стороны температура всегда поддерживается постоянной Т 2 = 20 С. Определить температуру в центре пластины через 3 часа, если материал пластины имеет следующие теплофизические свойства: коэффициент теплопроводности = 1,7 Вт/(м·С), плотность = 3500 кг/м3, теплоемкость С р = 650 Дж/(кг·С).

2. Стенка изготовлена из теплозащитного материала Динас ДЛ-2 (ТУ 14-8-67-73) и имеет следующие теплофизические свойства: коэффициент теплопроводности = 0,6 Вт/(м·С), плотность = 1200 кг/м3, теплоемкость С р = 1200 Дж/(кг·С). Стенка толщиной 0,125 м в начальный момент времени имела температуру T 0 = 20 С. В момент времени t = 0 на внутренней стороне температура стала равной T 1 = 1700 С, а с другой стороны температура всегда поддерживается постоянной Т 2 = 20 С. Определить температуру в центре пластины через 1 час.

3. Изоляционная бадделеитовая (ТУ 14-8-248-77) пластина толщиной 0,02 м, являющаяся элементом внутренней стенки плазмохимического реактора, имеет следующие теплофизические свойства: коэффициент теплопроводности = 1,2 Вт/(м·С), плотность = 5100 кг/м3, теплоемкость С р = 550 Дж/(кг·С). До запуска устройства пластина находилась при постоянной температуре T 0 = 20 С. В момент времени t = 0 на внутренней стороне температура стала равной T 1 = 2000 С, а с другой стороны температура всегда поддерживается постоянной Т 2 = 20 С. Определить температуру в центре пластины через 1 минуту.

4. Реакционно-устойчивое покрытие толщиной 1 мм, нанесенное на не пропускающее тепло тело и находящееся при начальной температуре T 0 = 20 С имеет следующие теплофизические свойства: коэффициент теплопроводности = 1,7 Вт/(м·С), плотность = 3500 кг/м3, теплоемкость С р = 650 Дж/(кг·С). В момент времени t = 0 с внешней стороны приложен тепловой поток плотностью q = 5 · 104 Вт/м2.

Определить температуру внутренней поверхности покрытия через 30 с нагрева.

5. Датчик плотности теплового потока представляет из.

себя медную пластинку, в центре которой заделана термопара. Толщина пластинки равна 5 мм. Начальная температура T 0 = 20 С. В момент времени t = 0 с внешней стороны приложен тепловой поток плотностью q = 1 · 107 Вт/м2. Определить температуру в месте заделки термопары через 1 с нагрева, если внутренняя поверхность датчика надежно теплоизолирована.

6. Стенки выходного канала плазмотрона, изготовленные из меди толщиной 10 мм, до включения плазмотрона имели температуру T 0 = 20 С. С внешней стороны выходной канал охлаждается водой температурой T 1 = 20 С, расход жидкости поддерживается постоянным, обеспечивающим интенсивность теплообмена с коэффициентом теплоотдачи 1 = 4 · 104 Вт/(м2·°С). Внутри канала после запуска плазмотрона движется нагретый в электрической дуге газ с температурой T 2 = 3000 С, с коэффициент теплоотдачи имеющем следующее значение 2 = 1,5 · 103 Вт/(м2·°С). Определить температуру внешней стенки канала плазмотрона через 3 с после его включения.

7. При плазменном декорировании строительных материалов плазменная струя оплавляет поверхность строительного изделия, за счет чего образуется защитно-декоративное стекловидное покрытие. Определить температуру поверхности строительного изделия через 1 секунду с момента начала воздействия плазменного потока с температурой T g = 3000 °С при коэффициенте теплоотдачи g = 1,5 · 103 Вт/(м2·°С), если материал имеет следующие теплофизические свойства: коэффициент теплопроводности S = 0,3 Вт/(м·°С), плотность = 1500 кг/м3, теплоемкость С р = 800 Дж/(кг·С).

8. Определить температурное поле в медной пластине через 5, 10, 30 и 60 секунд. Толщина пластины L = 0,3 м. Начальная температура T 0 = 20 С. На границе x = 0 приложен тепловой поток плотностью q = 1 · 106 Вт/м2, а граница x = L подвержена воздействию внешней среды температура которой T e = 300 С, с коэффициентом теплоотдачи имеющим следующее значение e = 102 Вт/(м2·°С). В направлении оси y пластина является однородной и достаточно длинной (неограниченной).

9. Определить температурное поле в медной пластине через 30, 180 и 600 секунд. Толщина пластины L = 0,3 м. Начальная температура T 0 = 50 С. На границе x = 0 пластина контактирует с внешней средой с температурой T e = –30 С, здесь коэффициент теплоотдачи e = 103 Вт/(м2·°С), а граница x = L подвержена воздействию внешней среды с температурой T e = 10 С, здесь коэффициент теплоотдачи e == 5 · 102 Вт/(м2·°С). В направлении оси 0Y пластина является однородной и неограниченной.

10. Определить температурное поле в составной пластине через 30, 180 и 600 секунд. Толщина пластины L = 0,3 м. Будем полагать, что толщины составных частей одинаковые. Начальная температура T 0 = 10 С. Одна часть пластины стальная, другая медная. На границе x = 0 поддерживается постоянная температура T = 100 С, здесь коэффициент теплоотдачи e = 103 Вт/(м2·°С), а на границе x = L T = 50 С. В направлении оси 0Y пластина является однородной и достаточно длинной (неограниченной).

11. Определить температурное поле в неограниченной серебряной пластине через 1, 5 и 10 секунд. Толщина пластины L = 0,3 м. Начальная температура T 0 = 10 С. Одна часть пластины стальная, другая медная. На границе x = 0 и x = L осуществляется теплообмен с окружающей средой – температура T e = 60 С, здесь коэффициент теплоотдачи e = 50 Вт/(м2·°С). В пластине равномерно распределены внутренние источники тепла мощностью Q(x). Данные источL L 3L ники находятся в точках x A. В связи с этим q = 10 Вт/м. В направлении оси y пластина является однородной и достаточно длинной (неограниченной).

12. Определить температурное поле в свинцовой пластине через 60 секунд. Толщина пластины L x = L y = 0,3 м.

Горизонтальные границы являются адиабатическими. На границе x = 0 поддерживается постоянная температура T = 80 С, а на границе x = L поддерживается постоянная температура T = 30 С.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

1. Лыков, А.В. Теория теплопроводности / А.В. Лыков. – М. :

Высшая школа, 1967. – 600 с.

2. Кузнецов, Г.В. / Разностные методы решения задач теплопроводности: учебное пособие / Г.В. Кузнецов, М.А. Шеремет. – Томск: Изд-во ТПУ, 2007. – 172 с.

3. Самарский, А.А. Теория разностных схем / А.А. Самарский – М. : Наука, 1977. – 656 с.

4. Патанкар, С.В. Численное решение задач теплопроводности и конвективного теплообмена при течении в каналах / С.В. Патанкар. – Пер. с англ. Е.В. Калабина; под. ред.

Г.Г. Янькова. – М. : Изд-во МЭИ, 2003. – 312 с.

Теплофизические свойства металлов Алюминий (чистый) Силумин(87%Al13%Si) Медь(чистая) Углеродистая сталь Хромистая сталь Никелевая сталь Марганцевая сталь (Mn1213% Ni3%) Вольфрамовая сталь (W56%, TM-1)

«ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ САМАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ МЕХАНИКО–МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ Кафедра информатики и вычислительной математики Подготовка и оформление курсовых и дипломных работ Методические указания для студентов специальности 010503 Математическое обеспечение и администрирование информационных систем Издательство Универс-групп 2005 Печатается по решению Редакционно-издательского. »

«С.Ф. Соболев, Ю.П. Кузьмин МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО РАЗРАБОТКЕ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ ИЗГОТОВЛЕНИЯ ДЕТАЛЕЙ МЕХАНИЧЕСКОЙ ОБРАБОТКОЙ Санкт-Петербург 2007 0 МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ, МЕХАНИКИ И ОПТИКИ С.Ф. Соболев, Ю.П. Кузьмин МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО РАЗРАБОТКЕ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ ИЗГОТОВЛЕНИЯ ДЕТАЛЕЙ МЕХАНИЧЕСКОЙ

«Проект План изданий учебной и научной литературы на 1 полугодие 2011 года Форма Форма № Авторы Название Вид издания Объем обуч. издания Факультет информационных технологий и машиноведения Кафедра теоретической и прикладной механики 1 Шарапин И. А., Шиянова Т. Г. Расчет элементов зубчатой передачи Учебное пособие Все Печатное Методические 2 Рудая М. Р., Шим В. В., Майоров А. М. Кинематический и силовой расчеты привода Все ЭИ указания Сборник заданий для выполнения курсового проекта по. »

«Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования ПЕТРОЗАВОДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ (ПетрГУ) БЕЛЯКОВ Ю.С. ИЗБРАННЫЕ МАТЕМАТИЧЕСКИЕ ВОПРОСЫ ЭЛЕКТРОЭНЕРГЕТИКИ Учебное пособие Раздел 2. Методы математического анализа электроэнергетических систем Петрозаводск Издательство ПетрГУ 2013 1 УДК 517.53 ББК Б Рецензенты: ст. научный сотрудник института прикладных математических исследований. »

«Министерство образования и науки Российской Федерации Сыктывкарский лесной институт (филиал) федерального государственного бюджетного образовательного учреждения высшего профессионального образования Санкт-Петербургский государственный лесотехнический университет имени С. М. Кирова Кафедра Электрификация и механизация сельского хозяйства СВЕТОТЕХНИКА И ЭЛЕКТРОТЕХНОЛОГИЯ Учебно-методический комплекс по дисциплине для студентов специальности 110302 Электрификация и автоматизация сельского. »

«ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования Ивановская государственная текстильная академия (ИГТА) Кафедра организации производства и логистики МЕТОДИЧЕСКИЕ УКАЗАНИЯ к выполнению курсовой работы ОРГАНИЗАЦИЯ ПРОИЗВОДСТВЕННОГО ПРОЦЕССА для студентов специальности 060800, обучающихся по сокращенной общеобразовательной программе ИВАНОВО 2004 В данных методических указаниях приводятся общие положения по обоснованию и выполнению. »

«Приложение 3 Титульный лист программы дисциплины ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования Уральский государственный университет им. А.М. Горького ИОНЦ Физика в биологии и медицине Математико — механический факультет Теоретической механики кафедра Методы экспериментальной механики живых систем Методические указания Подпись руководителя ИОНЦ Дата Екатеринбург 2007 Методические указания к изучению лабораторного практикума. »

«МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ, МЕХАНИКИ И ОПТИКИ А.М. Ефимов ОПТИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ И МЕХАНИЗМЫ ИХ ФОРМИРОВАНИЯ Учебное пособие Санкт-Петербург 2008 1 Ефимов А.М. Оптические свойства материалов и механизмы их формирования. – СПб: СПбГУИТМО., 2008. – 103 с. Настоящее издание представляет собой учебное пособие к образовательному модулю ОПД.Ф.07 Оптическое. »

«Министерство образования и науки Самарской области Министерство имущественных отношений Самарской области Государственное бюджетное образовательное учреждение среднего профессионального образования Тольяттинский индустриально-педагогический колледж (ГБОУ СПО ТИПК) МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЛАБОРАТОРНЫХ И ПРАКТИЧЕСКИХ РАБОТ ПО МАТЕРИАЛОВЕДЕНИЮ для студентов специальностей 190631 Техническое обслуживание и ремонт автомобильного транспорта 051001 Профессиональное обучение (отрасль –. »

«Министерство образования и науки РФ Государственное общеобразовательное учреждение высшего профессионального образования САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЛЕСОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ имени С.М. Кирова кафедра Технологии лесного машиностроения и ремонта ПРОИЗВОДСТВЕННО-ТЕХНИЧЕСКАЯ ИНФРАСТРУКТУРА СЕРВИСНОГО ОБСЛУЖИВАНИЯ ИЗДЕЛИЙ Методические указания по практическим занятиям для студентов специальности 19.06.03 Санкт-Петербург 2011 Рассмотрены и рекомендованы к изданию методической комиссией. »

«1 ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ЗДРАВООХРАНЕНИЮ И СОЦИАЛЬНОМУ РАЗВИТИЮ Государственное образовательное учреждение высшего профессионального образования Российский государственный медицинский университет Федерального агентства по здравоохранению и социальному развитию ФАРМАКОЛОГИЯ СНА Учебное пособие Утверждено на ЦКМС ГОУ ВПО РГМУ Росздрава Москва 2009 2 Р е ц е н з е н т ы: ведущий научный сотрудник лаборатории нейрохимической фармакологии НИИ фармакологии РАМН кандидат медицинских наук В.С.Кудрин;. »

«ФЕДЕРАЛЬНОЕ АГЕНТСТВО МОРСКОГО И РЕЧНОГО ТРАНСПОРТА ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИ МОРСКОЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ имени адмирала Г.И. Невельского В.Ф. Веревкин ДИПЛОМНОЕ ПРОЕКТИРОВАНИЕ Методические указания для курсантов специальности Эксплуатация судового электрооборудования и средств автоматики (Издание второе, переработанное и дополненное) Владивосток 2008 Позиция № 226 в плане издания учебной литературы МГУ на 2008 г. »

«МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЛАБОРАТОРНЫХ РАБОТ 4 Лабораторная работа № 1 ИССЛЕДОВАНИЕ ВЛИЯНИЯ МАКРОСТРУКТУРЫ НА ФИЗИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ Вопросы допуска к выполнению лабораторной работы 1. Классификация строительных материалов по назначению. 2. Что служит сырьем для производства строительных материалов? 3. Чем отличаются искусственно полученные материалы от природных? 4. Классификация свойств строительных материалов. 5. От каких факторов зависят следующие свойства материалов: –. »

«РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ 9/24/1 Одобрено кафедрой Управление эксплуатационной работой МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО РАЗРАБОТКЕ И ОФОРМЛЕНИЮ ДИПЛОМНЫХ ПРОЕКТОВ для студентов — дипломников специальности 190701 Организация перевозок и управление на транспорте (железнодорожный транспорт) (Д) Москва – 2008 М е т о д и ч е с к и е у к а з а н и я с о с т а в и л и : Апатцев В. И., Биленко Г.М., Бухало Г.И., Голубев Б.Л., Голубкин Б.П., Гершвальд А. С. »

«Министерство образования Российской Федерации Ивановская государственная текстильная академия Кафедра механической технологии текстильных материалов МЕТОДИЧЕСКИЕ УКАЗАНИЯ к проведению учебной практики для студентов 2 курса специальности 280500 Технология трикотажного производства Иваново — 2000 1 Настоящие методические указания предназначены для студентов 2 курса технологического факультета специальности 280500 “Технология трикотажного производства”. В них приводятся содержание практики и. »

«ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОУ ВПО КРАСНОЯРСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ им. В.П. АСТАФЬЕВА Н.В. Полева БИОХИМИЯ Учебное пособие для студентов высших учебных заведений, обучающихся по специальности 032101 Физическая культура и спорт КРАСНОЯРСК 2009 1 ББК 28.072я73 П49 Печатается по решению редакционно-издательского совета ГОУ ВПО Красноярский государственный педагогический университет им. В. П. Астафьева Рецензенты: Киршина Е.Д., канд. пед. наук, доцент Наймушина. »

«Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение Высшего профессионального образования Амурский государственный университет УТВЕРЖДАЮ Зав. кафедрой энергетики _ Ю.В.Мясоедов _2012 г. ТЕЛЕМЕХАНИЗАЦИЯ УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС ПО ДИСЦИПЛИНЕ для специальностей 140204.65 – Электрические станции 140205.65 – Электроэнергетические системы и сети Составитель: Ю.В. Мясоедов Благовещенск 2012 г. СОДЕРЖАНИЕ 1. Рабочая программа. »

«Кафедра фармакологии им. профессора М.В.Кораблёва Методические указания для студентов Лечебный факультет и отделение иностранных студентов Занятие № 1 (3 – 7 февраля 2014 года). Тема: Противоаритмические средства. Домашнее задание: 1. Основные (контрольные) вопросы темы: 1.1. Классификация средств для лечения тахиаритмий (по Воген — Вильямсу, с названием основных препаратов). Другие средства для лечения тахиаритмий. 1.2. Краткая характеристика тахиаритмий; сравнительная эффективность. »

«Министерство образования и науки Российской федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Амурский государственный университет Кафедра автоматизации производственных процессов и электротехники УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС ДИСЦИПЛИНЫ МЕХАНИКА Направление подготовки: 280700.62 Техносферная безопасность По профилю: Безопасность жизнедеятельности в техносфере Квалификация (степень) выпускника: бакалавр Благовещенск 2012 г. УМКД. »

«ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОУ ВПО Уральский государственный лесотехнический университет Факультет лесомеханический Кафедра начертательной геометрии и машиностроительного черчения Дисциплина начертательная геометрия и инжереная графика (Наименование учебной дисциплины по учебному плану) Направление 261200 Технология полиграфического и упаковочного производства Специальность 261201 Технология и дизайн упаковочного производства (Код и наименование специальности по классификатору. »

© 2013 www.diss.seluk.ru — «Бесплатная электронная библиотека — Авторефераты, Диссертации, Монографии, Методички, учебные программы»

Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.
Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.