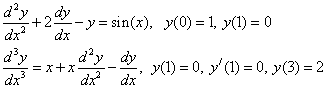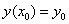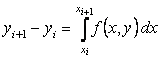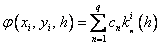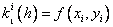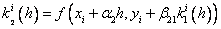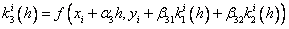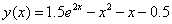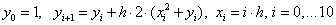Методы конечных разностей
Достоинство этих методов состоит в том, что они сводят решение краевой задачи для дифференциального уравнения к решению системы алгебраических уравнений относительно значений искомой функции на заданном множестве точек. Это достигается заменой производных, входящих в дифференциальное уравнение, их конечно-разностными аппроксимациями.
Рассмотрим сущность такого метода решения для дифференциального уравнения второго порядка (1.41) при заданных граничных условиях (1.42). Разобьем отрезок [0,1] на n равных частей точками xi= ih(i= 0,1. , n). Решение краевой задачи (1.41), (1.42) сведем к вычислению значений сеточной функции yi в узловых точках xi. Для этого напишем уравнение (1.42) для внутренних узлов:

Заменим производные, входящие в эти соотношения, их конечно-разностными аппроксимациями:


Подставляя эти выражения в (1.49), получаем систему разностных уравнений:

являющуюся системой n-1 алгебраических уравнений относительно значений сеточной функции 
На практике часто граничные условия задают в более общем виде (1.38):

В этом случае граничные условия также должны представляться в разностном виде путем аппроксимации производных Y‘(0) и Y‘(1) с помощью конечно-разностных соотношений. Если использовать односторонние разности (соответствующий шаблон показан на рис. 1.7, а),при которых производные аппроксимируются с первым порядком точности, то разностные граничные условия примут вид

Из этих соотношений легко находятся значения y0, yn.
Однако, как правило, предпочтительнее аппроксимировать производные, входящие в (1.52), со вторым порядком точности с помощью центральных разностей:
Рис. 1.7. Аппроксимация граничных условий
В данные выражения входят значения сеточной функции 
Аппроксимировать граничные условия со вторым порядком можно и иначе (см. рис. 1.7, в). В этом случае используют аппроксимации:
Таким образом, решение краевой задачи для дифференциального уравнения сведено к решению системы алгебраических уравнений вида (1.51). Эта система является линейной или нелинейной в зависимости от того, линейно или нелинейно дифференциальное уравнение (1.41). Методы решения таких систем рассмотрены ранее.
Рассмотрим подробнее один частный случай, который представляет интерес с точки зрения практических приложений и позволяет проследить процесс построения разностной схемы. Решим краевую задачу для линейного дифференциального уравнения второго порядка

с граничными условиями вида
Разобьем отрезок [0,1] на части с постоянным шагом h с помощью узлов 
Обозначим рi, fiсоответственно величины 

Получилась система n—1 линейных уравнений, число которых совпадает с числом неизвестных значений сеточной функции 
Решив систему уравнений (1.56) с учетом условий (1.57), найдем значения сеточной функции, которые приближенно равны значениям искомой функции. Покажем, что такое решение существует и сходится к точному решению при h→ 0.
Для доказательства существования решения рассмотрим систему линейных уравнений (1.56). Ее матрица является трехдиагональной; на главной диагонали находятся элементы 
Что касается сходимости решения, то здесь имеет место следующее утверждение.
Утверждение. Если функции р(х) и f(x) дважды непрерывно дифференцируемы, то при h→0 разностное решение равномерно сходится к точному со скоростью O(h2).
Это — достаточное условие сходимости метода конечных разностей для краевой задачи (1.54), (1.55).
Система линейных алгебраических уравнений (1.56) с трехдиагональной матрицей может быть решена методом прогонки. При этом условие р(х) > 0 гарантирует выполнение условия устойчивости прогонки.
Этот метод на практике используется также и при р(х) Будет полезно почитать по теме:
Метод конечных разностей решения обыкновенных дифференциальных уравнений
Pers.narod.ru. Обучение. Лекции по численным методам. Численное решение обыкновенных дифференциальных уравнений
5. Численное решение обыкновенных дифференциальных уравнений
Многие задачи науки и техники сводятся к решению обыкновенных дифференциальных уравнений (ОДУ). ОДУ называются такие уравнения, которые содержат одну или несколько производных от искомой функции. В общем виде ОДУ можно записать следующим образом:
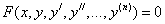
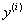
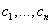
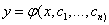
Для выделения единственного решения необходимо задать n дополнительных условий. В зависимости от способа задания дополнительных условий существуют два различных типа задач: задача Коши и краевая задача. Если дополнительные условия задаются в одной точке, то такая задача называется задачей Коши. Дополнительные условия в задаче Коши называются начальными условиями. Если же дополнительные условия задаются в более чем одной точке, т.е. при различных значениях независимой переменной, то такая задача называется краевой. Сами дополнительные условия называются краевыми или граничными.
Ясно, что при n=1 можно говорить только о задачи Коши.
Примеры постановки задачи Коши:
Примеры краевых задач:
Решить такие задачи аналитически удается лишь для некоторых специальных типов уравнений.
Численные методы решения задачи Коши для ОДУ первого порядка
Постановка задачи. Найти решение ОДУ первого порядка
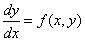
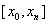
При нахождении приближенного решения будем считать, что вычисления проводятся с расчетным шагом 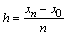
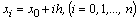
Целью является построение таблицы
т.е. ищутся приближенные значения y в узлах сетки.
Интегрируя уравнение на отрезке 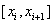
Вполне естественным (но не единственным) путем получения численного решения является замена в нем интеграла какой–либо квадратурной формулой численного интегрирования. Если воспользоваться простейшей формулой левых прямоугольников первого порядка
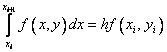
то получим явную формулу Эйлера:
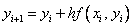
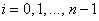
Зная 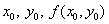
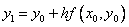
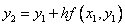
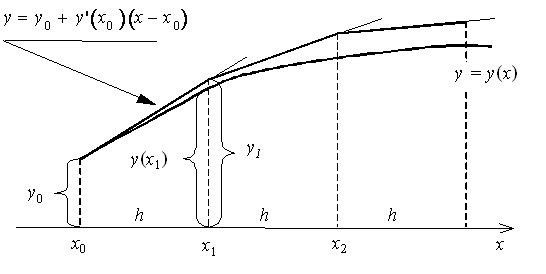
Геометрическая интерпретация метода Эйлера:
Пользуясь тем, что в точке x0 известно решение y(x0) = y0 и значение его производной 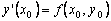
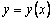
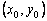
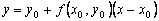
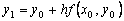
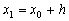
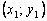
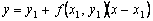
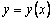
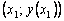
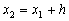
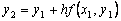
Явный метод Эйлера имеет первый порядок точности или аппроксимации.
Если использовать формулу правых прямоугольников: 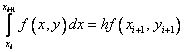
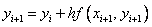
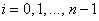
Этот метод называют неявным методом Эйлера, поскольку для вычисления неизвестного значения 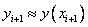
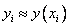
Неявный метод Эйлера имеет первый порядок точности или аппроксимации.
Модифицированный метод Эйлера: в данном методе вычисление 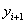
Данная схема называется еще методом предиктор – корректор (предсказывающее – исправляющее). На первом этапе приближенное значение предсказывается с невысокой точностью (h), а на втором этапе это предсказание исправляется, так что результирующее значение имеет второй порядок точности.
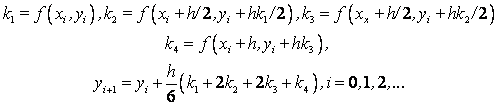
Методы Рунге – Кутта: идея построения явных методов Рунге–Кутты p–го порядка заключается в получении приближений к значениям y(xi+1) по формуле вида
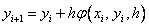
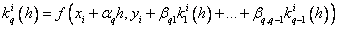
Здесь an, bnj, pn, 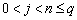
При построения методов Рунге–Кутты параметры функции 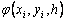
Схема Рунге – Кутта четвертого порядка точности:
Пример. Решить задачу Коши:
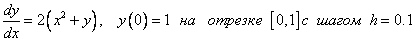
Рассмотреть три метода: явный метод Эйлера, модифицированный метод Эйлера, метод Рунге – Кутта.
Точное решение:
Расчетные формулы по явному методу Эйлера для данного примера:
Расчетные формулы модифицированного метода Эйлера:
http://pers.narod.ru/study/methods/05.html