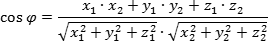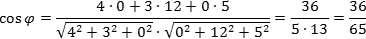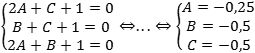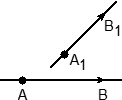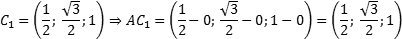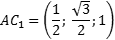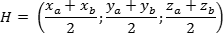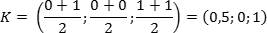Метод координат при решении системы уравнений

Метод координат в пространстве

Для того, чтобы использовать метод координат, надо хорошо знать формулы. Их три:

Главная формула — косинус угла φ между векторами a = (x₁; y₁; z₁) и b = (x₂; y₂; z₂):

На первый взгляд, выглядит угрожающе, но достаточно немного практики — и все будет работать великолепно.

Задача. Найти косинус угла между векторами a = (4; 3; 0) и b = (0; 12; 5).

Решение. Поскольку координаты векторов нам даны, подставляем их в первую формулу:

Задача. Составить уравнение плоскости, проходящей через точки M = (2; 0; 1), N = (0; 1; 1) и K = (2; 1; 0), если известно, что она не проходит через начало координат.

Решение. Общее уравнение плоскости: Ax + By + Cz + D = 0, но, поскольку искомая плоскость не проходит через начало координат — точку (0; 0; 0) — то положим D = 1. Поскольку эта плоскость проходит через точки M, N и K, то координаты этих точек должны обращать уравнение в верное числовое равенство.

Подставим вместо x, y и z координаты точки M = (2; 0; 1). Имеем:
A · 2 + B · 0 + C · 1 + 1 = 0 ⇒ 2A + C + 1 = 0;

Аналогично, для точек N = (0; 1; 1) и K = (2; 1; 0) получим уравнения:
A · 0 + B · 1 + C · 1 + 1 = 0 ⇒ B + C + 1 = 0;
A · 2 + B · 1 + C · 0 + 1 = 0 ⇒ 2A + B + 1 = 0;

Итак, у нас есть три уравнения и три неизвестных. Составим и решим систему уравнений:

Получили, что уравнение плоскости имеет вид: − 0,25x − 0,5y − 0,5z + 1 = 0.

Задача. Плоскость задана уравнением 7x − 2y + 4z + 1 = 0. Найти координаты вектора, перпендикулярного данной плоскости.

Решение. Используя третью формулу, получаем n = (7; − 2; 4) — вот и все!

Вычисление координат векторов

А что, если в задаче нет векторов — есть только точки, лежащие на прямых, и требуется вычислить угол между этими прямыми? Все просто: зная координаты точек — начала и конца вектора — можно вычислить координаты самого вектора.

Чтобы найти координаты вектора, надо из координат его конца вычесть координаты начала.

Эта теорема одинаково работает и на плоскости, и в пространстве. Выражение «вычесть координаты» означает, что из координаты x одной точки вычитается координата x другой, затем то же самое надо сделать с координатами y и z. Вот несколько примеров:

Задача. В пространстве расположены три точки, заданные своими координатами: A = (1; 6; 3), B = (3; − 1; 7) и C = (− 4; 3; − 2). Найти координаты векторов AB, AC и BC.

Рассмотрим вектор AB: его начало находится в точке A, а конец — в точке B. Следовательно, чтобы найти его координаты, надо из координат точки B вычесть координаты точки A:
AB = (3 − 1; − 1 − 6; 7 − 3) = (2; − 7; 4).

Аналогично, начало вектора AC — все та же точка A, зато конец — точка C. Поэтому имеем:
AC = (− 4 − 1; 3 − 6; − 2 − 3) = (− 5; − 3; − 5).

Наконец, чтобы найти координаты вектора BC, надо из координат точки C вычесть координаты точки B:
BC = (− 4 − 3; 3 − (− 1); − 2 − 7) = (− 7; 4; − 9).

Ответ: AB = (2; − 7; 4); AC = (− 5; − 3; − 5); BC = (− 7; 4; − 9)

Обратите внимание на вычисление координат последнего вектора BC: очень многие ошибаются, когда работают с отрицательными числами. Это касается переменной y: у точки B координата y = − 1, а у точки C y = 3. Получаем именно 3 − (− 1) = 4, а не 3 − 1, как многие считают. Не допускайте таких глупых ошибок!

Вычисление направляющих векторов для прямых

Если вы внимательно прочитаете задачу C2, то с удивлением обнаружите, что никаких векторов там нет. Там только прямые да плоскости.

Для начала разберемся с прямыми. Здесь все просто: на любой прямой найдутся хотя бы две различные точки и, наоборот, любые две различные точки задают единственную прямую.

Кто-нибудь понял, что написано в предыдущем абзаце? Я и сам не понял, поэтому объясню проще: в задаче C2 прямые всегда задаются парой точек. Если ввести систему координат и рассмотреть вектор с началом и концом в этих точках, получим так называемый для прямой:

Зачем нужен этот вектор? Дело в том, что — это угол между их направляющими векторами. Таким образом, мы переходим от непонятных прямых к конкретным векторам, координаты которых легко считаются. Насколько легко? Взгляните на примеры:

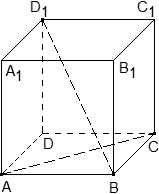
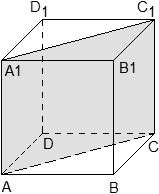
Задача. В кубе ABCDA₁B₁C₁D₁ проведены прямые AC и BD₁. Найдите координаты направляющих векторов этих прямых.

Поскольку длина ребер куба в условии не указана, положим AB = 1. Введем систему координат с началом в точке A и осями x, y, z, направленными вдоль прямых AB, AD и AA₁ соответственно. Единичный отрезок равен AB = 1.

Теперь найдем координаты направляющего вектора для прямой AC. Нам потребуются две точки: A = (0; 0; 0) и C = (1; 1; 0). Отсюда получаем координаты вектора AC = (1 − 0; 1 − 0; 0 − 0) = (1; 1; 0) — это и есть направляющий вектор.

Теперь разберемся с прямой BD₁. На ней также есть две точки: B = (1; 0; 0) и D₁ = (0; 1; 1). Получаем направляющий вектор BD₁ = (0 − 1; 1 − 0; 1 − 0) = (− 1; 1; 1).

Ответ: AC = (1; 1; 0); BD₁ = (− 1; 1; 1)

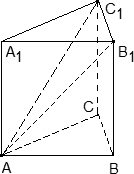
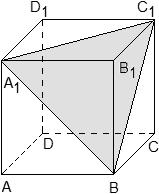
Задача. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, проведены прямые AB₁ и AC₁. Найдите координаты направляющих векторов этих прямых.

Введем систему координат: начало в точке A, ось x совпадает с AB, ось z совпадает с AA₁, ось y образует с осью x плоскость OXY, которая совпадает с плоскостью ABC.

Для начала разберемся с прямой AB₁. Тут все просто: у нас есть точки A = (0; 0; 0) и B₁ = (1; 0; 1). Получаем направляющий вектор AB₁ = (1 − 0; 0 − 0; 1 − 0) = (1; 0; 1).

Теперь найдем направляющий вектор для AC₁. Все то же самое — единственное отличие в том, что у точки C₁ иррациональные координаты. Итак, A = (0; 0; 0), поэтому имеем:

Небольшое, но очень важное замечание насчет последнего примера. Если начало вектора совпадает с началом координат, вычисления резко упрощаются: координаты вектора просто равны координатам конца. К сожалению, это верно лишь для векторов. Например, при работе с плоскостями присутствие на них начала координат только усложняет выкладки.

Вычисление нормальных векторов для плоскостей

Нормальные векторы — это не те векторы, у которых все в порядке, или которые чувствуют себя хорошо. По определению, нормальный вектор (нормаль) к плоскости — это вектор, перпендикулярный данной плоскости.

Другими словами, — это вектор, перпендикулярный любому вектору в данной плоскости. Наверняка вы встречали такое определение — правда, вместо векторов речь шла о прямых. Однако чуть выше было показано, что в задаче C2 можно оперировать любым удобным объектом — хоть прямой, хоть вектором.

Еще раз напомню, что всякая плоскость задается в пространстве уравнением Ax + By + Cz + D = 0, где A, B, C и D — некоторые коэффициенты. Не умаляя общности решения, можно полагать D = 1, если плоскость не проходит через начало координат, или D = 0, если все-таки проходит. В любом случае, координаты нормального вектора к этой плоскости равны n = (A; B; C).

Итак, плоскость тоже можно успешно заменить вектором — той самой нормалью. Всякая плоскость задается в пространстве тремя точками. Как найти уравнение плоскости (а следовательно — и нормали), мы уже обсуждали в самом начале статьи. Однако этот процесс у многих вызывает проблемы, поэтому приведу еще парочку примеров:

Задача. В кубе ABCDA₁B₁C₁D₁ проведено сечение A₁BC₁. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA₁ соответственно.

Поскольку плоскость не проходит через начало координат, ее уравнение выглядит так: Ax + By + Cz + 1 = 0, т.е. коэффициент D = 1. Поскольку эта плоскость проходит через точки A₁, B и C₁, то координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 + 1 = 0 ⇒ C + 1 = 0 ⇒ C = − 1;

Аналогично, для точек B = (1; 0; 0) и C₁ = (1; 1; 1) получим уравнения:
A · 1 + B · 0 + C · 0 + 1 = 0 ⇒ A + 1 = 0 ⇒ A = − 1;
A · 1 + B · 1 + C · 1 + 1 = 0 ⇒ A + B + C + 1 = 0;

Но коэффициенты A = − 1 и C = − 1 нам уже известны, поэтому остается найти коэффициент B:
B = − 1 − A − C = − 1 + 1 + 1 = 1.

Получаем уравнение плоскости: − A + B − C + 1 = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; − 1).

Задача. В кубе ABCDA₁B₁C₁D₁ проведено сечение AA₁C₁C. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA₁ соответственно.

В данном случае плоскость проходит через начало координат, поэтому коэффициент D = 0, а уравнение плоскости выглядит так: Ax + By + Cz = 0. Поскольку плоскость проходит через точки A₁ и C, координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 = 0 ⇒ C = 0;

Аналогично, для точки C = (1; 1; 0) получим уравнение:
A · 1 + B · 1 + C · 0 = 0 ⇒ A + B = 0 ⇒ A = − B;

Положим B = 1. Тогда A = − B = − 1, и уравнение всей плоскости имеет вид: − A + B = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; 0).

Вообще говоря, в приведенных задачах надо составлять систему уравнений и решать ее. Получится три уравнения и три переменных, но во втором случае одна из них будет свободной, т.е. принимать произвольные значения. Именно поэтому мы вправе положить B = 1 — без ущерба для общности решения и правильности ответа.

Координаты середины отрезка

Очень часто в задаче C2 требуется работать с точками, которые делят отрезок пополам. Координаты таких точек легко считаются, если известны координаты концов отрезка.

Итак, пусть отрезок задан своими концами — точками A = (x_a; y_a; z_a) и B = (x_b; y_b; z_b). Тогда координаты середины отрезка — обозначим ее точкой H — можно найти по формуле:

Другими словами, координаты середины отрезка — это среднее арифметическое координат его концов.

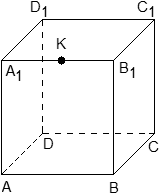
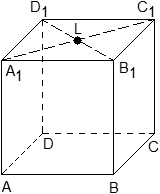
Задача. Единичный куб ABCDA₁B₁C₁D₁ помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA₁ соответственно, а начало координат совпадает с точкой A. Точка K — середина ребра A₁B₁. Найдите координаты этой точки.

Поскольку точка K — середина отрезка A₁B₁, ее координаты равных среднему арифметическому координат концов. Запишем координаты концов: A₁ = (0; 0; 1) и B₁ = (1; 0; 1). Теперь найдем координаты точки K:

Задача. Единичный куб ABCDA₁B₁C₁D₁ помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA₁ соответственно, а начало координат совпадает с точкой A. Найдите координаты точки L, в которой пересекаются диагонали квадрата A₁B₁C₁D₁.

Из курса планиметрии известно, что точка пересечения диагоналей квадрата равноудалена от всех его вершин. В частности, A₁L = C₁L, т.е. точка L — это середина отрезка A₁C₁. Но A₁ = (0; 0; 1), C₁ = (1; 1; 1), поэтому имеем:

Метод координат. 9-й класс

Класс: 9

Презентация к уроку

Профиль класса: физико-математический

Тип урока – повторительно-обобщающий, 45 мин.

Цели урока:

• Закрепить понятия по теме “Метод координат”.
• Развивать умение применять формулы простейших задач к решению примеров.
• Воспитывать культуру корректно отвечать определения и формулы, аккуратно оформлять записи в тетрадях.

Ход урока

1.1. Взаимное приветствие учителя и учащихся

1.2. Сообщение темы и цели урока.

1.3. Настрой на урок.

Цель: Выяснить у ответственных учеников о готовности учащихся к уроку.

II. Проверка домашнего задания: №902; №1000а; №1044а; 1041а.

Слайды № 3- №4;

3 мин.№900. Дано: ABC, A(4;8), B(12;11), C(7;0)

Доказать: ABC – равнобедренный, но не равносторонний.

1) d=

AB=

2) AC=

3) BC=

Так как AB=AC, то ABC – равнобедренный с основанием BC.

Ответ: ABC– равнобедренный с основанием BC.

№1000.

Выяснить: Является ли это уравнение уравнением окружности, если “да”, то найти координаты центра и радиус окружности.

Решение: Так как уравнение имеет вид: (x-x₀) 2 +(y-y₀) 2 = R 2 , где (x₀;y₀) — координаты центра; R — радиус окружности,

(1;-2) — координаты центра, R 2 =25;

Ответ: R=5; (1;-2) – координаты центра данной окружности.

№1041.

Дано: , ,

Найти:

=

=

Ответ:

№1044(а).

Дано:

Найти:

x₁x₂+y₁y₂

Ответ: -2,5III. Повторительно-обобщающий этап:

а) “Из истории возникновения и развития метода координат”. Приготовил: Патрашкин Егор.

Первоначально идея координат зародилась в древности в связи с потребностями астрономии, географии, живописи. Так, на стене одной из древнеегипетских погребальных камер была обнаружена квадратная сетка (палетка), которой пользовались для увеличения изображений

Древнегреческий астроном Клавдий Птолимей применил географические координаты для определения местонахождения мореплавателя. Идеей координат пользовались в середине века для определения положения светил на небе, для определения места на поверхности Земли. Прямоугольной сеткой пользовались художники эпохи Возрождения.

Применять координаты в математике впервые стали Ферма и Декарт. В 1637 году вышла книга Декарта Рассуждения о методе, в которой наряду с общими философскими рассуждениями о материи значительное место уделяется универсальной математике.

Декарт предложил новый метод координат, который позволил переходить от точки к паре чисел,

• от линии к уравнению,
• от геометрии к алгебре.

Заслуга Декарта состояла в том, что он ввел переменные координаты.

Так, в уравнении ах + ву = с,

буквы х и у стали рассматриваться не как неизвестные, а как переменные.

Метод координат позволяет строить графики уравнений, изображать геометрически различные зависимости, выраженные аналитически с помощью уравнений и формул, решать различные геометрические задачи с помощью алгебры. Термины абсцисса, ордината были введены в употребление Г. Лейбницем в 70, 80-е годы XVII в.

б) Презентация задач и решений этих задач по данной теме.

1. Приготовила Азанова Алена: Задача 1. Найдите координаты точки М, если М — середина АВ, А(-16;5); В(4;2).
2. Приготовил Иванов Георгий:Задача 2. Найдите длину отрезка АВ, если А(3;-2); В(3;0).
3. Приготовила Семенова Марина: Задача 3. Найдите длину отрезка АВ, если А(3;-2); В(3;0).

Выполнил Путрин Антон:

Дан треугольник ABC, где M – середина отрезка AB. Найти координаты M, если A(3;5), а B(3;8).

Геометрия. 11 класс

Конспект урока

Геометрия, 11 класс

Урок № 3. Координатный метод решения задач

Перечень вопросов, рассматриваемых в теме:

• специфика и преимущества решения задач в пространстве координатным методом;
• типы задач, решаемые координатным методом;
• этап решения задачи координатным методом;
• решение несложных задач методом координат.

Глоссарий по теме

Уравнение вида задает в пространстве плоскость α.

При этом вектор – это вектор, перпендикулярный плоскости α. Его называют вектор нормали, или нормальный вектор, или нормаль. Очевидно, что нормалью является любой вектор, коллинеарный вектору .

Вектор и любой коллинеарный ему вектор называются направляющим векторами прямой и прямой соответственно.

Шарыгин И.Ф. Геометрия. 10–11 кл. : учеб. для общеобразоват. Учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 163-170.

Потоскуев Е.В., Звавич Л. И. Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 353-260.

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

Работа по теме урока. Объяснение новой темы

Мы рассмотрели несложную задачу на применение метода координат в пространстве.

Векторы , угол между которыми мы искали, называются направляющими векторами прямой и прямой соответственно.

Рассмотрим этот метод более подробно.

Суть метода координат на плоскости и в пространстве заключается в следующем.

1. Ввести систему координат удобным образом (исходя их свойств заданной фигуры)
2. Записать условие задачи в координатах, определив во введенной системе координат координаты точек и/или векторов
3. Используя алгебраические преобразования, решить задачу
4. Интерпретировать полученный результат в соответствии с условием данной задачи

В рассмотренном нами примере, поскольку был дан куб, мы могли ввести систему координат с центром в любой его вершине.

В координатах удобно решать задачи, связанные с поиском расстояний и углов. Но для того чтобы его использовать, нужно знать некоторые формулы:

1. Угол между прямыми
2. Угол между прямой и плоскостью
3. Угол между плоскостями
4. Расстояние от точки до плоскости
5. Расстояние от точки до прямой в пространстве
6. Расстояние между скрещивающимися прямыми

Расстояние между параллельными плоскостями определяется как расстояние от точки, лежащей в одной плоскости, до другой плоскости.

Мы рассмотрим только первые четыре формулы.

Угол между прямыми

Если прямая задана двумя точками A и B, то известен направляющий вектор этой прямой с координатами <>. Пусть вторая прямая имеет направляющий вектор . Тогда угол между векторами вычисляется по формуле:

.

Дальше ищется арккосинус от найденного числа. Заметим, что если косинус получился отрицательным, то это значит, что угол между векторами тупой. Поэтому мы берем модуль получившегося числа.

Фактически мы уже рассмотрели пример вычисления угла между прямыми в пространстве.

Угол между прямой и плоскостью

Сначала рассмотрим уравнение плоскости, проходящей через три точки.

.

Вам известно, что в пространстве плоскость задается уравнением, аналогичным тому, которое на плоскости задает прямую.

Если линейное уравнение вида на плоскости задает прямую l, то уравнение вида задает в пространстве плоскость α. При этом вектор – это вектор, перпендикулярный плоскости α. Его называют вектор нормали, или нормальный вектор, или нормаль.

Вам известно, что три точки в пространстве определяют единственную плоскость. Поэтому, если заданы три точки, то мы можем найти уравнение плоскости

Мы можем подставить координаты заданных точек в уравнение плоскости и решить систему из трех уравнений с тремя переменными:

В этой системе четыре неизвестных, однако, мы можем избавиться от одной, если разделим все уравнения на D:

.

Для изучения данного способа в 11 классе на базовом уровне введение понятий матрица, определитель матрицы не желателен, данные понятия не входят в базовый курс изучения геометрии.

Иногда эта система оказывается несложной. Но иногда бывает трудно ее решить, и тогда можно использовать следующую формулу:

Обозначение |M| означает определитель матрицы М.

В нашем случае матрица представляет собой таблицу 3х3 элемента. И определитель |M| вычисляется следующим образом:

.

Таким образом, уравнение плоскости будет записано так:

Написать уравнение плоскости, проходящей через точки K(1; -2; 3), L (0; 1; 1), M (1; 0; 1).

.

Решая ее, получим значения А, В и С: . То есть уравнение плоскости имеет вид:

.

Ответ: .

Теперь запишем формулу угла между прямой и плоскостью.

Пусть дано уравнение плоскости: и известен — направляющий вектор прямой.

Тогда – синус угла между прямой и плоскостью.

Найдем угол между прямой и плоскостью. В качестве плоскости возьмем ту, уравнение которой мы только что написали:

Прямая проходит через точки Т(2; -1; 4) и Р(3; 2; 2).

Направляющий вектор прямой: .

Найдем синус угла между прямой и плоскостью:

.

Угол между прямой и плоскостью .

Ответ: .

Угол между плоскостями

уравнение первой плоскости:

уравнение второй плоскости:

Тогда — косинус угла между этими плоскостями.

Найдем угол между плоскостями:

и .

Найдем косинус угла между плоскостями:

.

Угол между плоскостями:

Ответ:

Расстояние от точки до плоскости

Пусть координаты точки: , уравнение плоскости: .

Тогда Расстояние от точки до плоскости вычисляется по формуле: .

Найдем расстояние от точки М(4; 3; 4) до плоскости .

.

Теперь рассмотрим решение задачи координатным методом с использованием рассмотренных формул.

АВС…D1 – куб с ребром 4. Найти расстояние от точки А до плоскости ЕКС (Е – середина D1C1, K – середина C1B1)

Введем систему координат с началом в вершине А так, как показано на рисунке:

Интересующие нас точки будут иметь координаты:

A(0; 0; 0), C(4; 4; 0), E(4; 2; 4), K(2; 4; 4).

Напишем уравнение плоскости ЕКС:

.

Решая ее, получим значения А, В, С и D: .

Уравнение плоскости имеет вид:

Теперь найдем расстояние от точки А до плоскости ЕКС: .

Ответ: .

Рассмотрим задачу (№14 из варианта ЕГЭ).

В кубе ABC…D₁ все рёбра равны 4. На его ребре BB₁ отмечена точка K так, что KB = 3. Через точки K и C₁ построена плоскость α, параллельная прямой BD₁.

а) Докажите, что A₁P : PB₁ = 2 : 1, где P — точка пересечения плоскости α с ребром A₁B₁.

б) Найдите угол наклона плоскости α к плоскости грани BB₁C₁C.

Переформулируем первый пункт этой задачи таким образом:

Проведем плоскость через точки Р, K и C₁ и докажем, что она параллельна прямой BD₁.

Введем систему координат так, как показано на рисунке:

Найдем координаты точек :

Р(; 0; 4), К(4; 0; 3),(4; 4; 4).

Напишем уравнение плоскости :

;

Решая ее, получим значения А, В, С и D: .

— уравнение плоскости

Теперь докажем, что плоскость параллельна прямой BD₁.

Найдем угол между прямой BD₁ и плоскостью .

Точки В и D₁ имеют координаты: В (4; 0; 0), D₁ (0; 4; 4).

Направляющий вектор прямой BD₁ – это вектор .

Он имеет координаты .

Теперь найдем синус угла между вектором и плоскостью .

.

В этом случае нам не нужно считать знаменатель дроби. Так как числитель получился равен 0, то дробь равна 0, то есть синус угла между плоскостью и прямой равен 0, значит, плоскости параллельны или совпадают. Но, так как точка В, например, в плоскости, очевидно, не лежит, то плоскости параллельны.

Это значит, что плоскость, параллельная прямой BD₁ и проходящая через точки действительно пересекает ребро A₁B₁в точке Р так, что A₁P : PB₁ = 2 : 1. Что и требовалось доказать.

Теперь рассмотри второй пункт задачи. Уравнение плоскости у нас есть. Плоскость BB₁C₁ параллельна координатной плоскости YOZ и проходит через точку

В(4; 0; 0). Поэтому она имеет уравнение .

То есть ее коэффициенты .

Найдем угол между плоскостями, используя формулу

Ответ: .