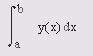20. Численное интегрирование методом квадратур
Численное интегрирование методом квадратур
Приведенные ниже функции осуществляют интегрирование и двойное интегрирование, используя квадратурную формулу Симпсона или метод Гаусса-Лобатто. Квадратура — численный метод нахождения площади под графиком функции/(т), т. е. вычисление определенного интеграла вида
В приведенных ниже формулах подынтегральное выражение fun обычно задается в форме дескриптора функции, поэтому с дидактическими целями используем нотацию @fun.
Функции quad и quadl используют два различных алгоритма квадратуры для вычисления определенного интеграла. Функция quad выполняет интегрирование по методу низкого порядка, используя рекурсивное правило Симпсона [4, 40]. Но она может быть более эффективной при негладких подынтегральных функциях или при низкой требуемой точности вычислений. Алгоритм quad в MATLAB 6 изменен по сравнению с предшествовавшими версиями, точность по умолчанию по сравнению с версиями 5.3х повышена в 1000 раз (с 10- 3 до 10- 6 ). Новая функция quadl (квадратура Лобатто) использует адаптивное правило квадратуры Гаусса— Лобатто очень высокого порядка. Устаревшая функция quads выполняла интегрирование, используя квадратурные формулы Ньютона—Котеса 8-го порядка [40]. Достижимая точность интегрирования гладких функций в MATLAB 6 поэтому также значительно выше, чем в предшествующих версиях.
quad(@fun,a.b) — возвращает численное значение определенного интеграла от заданной функции @fun на отрезке [а Ь]. Используется значительно усовершенствованный в MATLAB 6 адаптивный метод Симпсона;
quad(@fun,a.b.tol) — возвращает численное значение определенного интеграла с заданной относительной погрешностью tol. По умолчанию to1=l.e-6. Можно также использовать вектор, состоящий из двух элементов tol =[rel_tol abs_tol], чтобы точно определить комбинацию относительной и абсолютной погрешности;
quad(@fun,a.b,tol .trace) — возвращает численное значение определенного интеграла и при значении trace, не равном нулю, строит график, показывающий ход вычисления интеграла;
quad(@fun,a,b.tol,trace,PI,P2. ) — возвращает численное значение определенного интеграла по хот подынтегральной функции fun, использует дополнительные аргументы P1, P2. которые напрямую передаются в подынтегральную функцию: G=fun(X.Pl,P2. ). Примеры:
dblquad(@fun,inmin,inmax.outmin,outmax) — вычисляет и возвращает значение двойного интеграла для подынтегральной функции fun (Inner, outer), по умолчанию используя квадратурную функцию quad. Inner — внутренняя переменная, изменяющаяся на закрытом интервале от inmin до inmax, a outer — внешняя переменная, изменяющаяся на закрытом интервале от outmin до outmax. Первый аргумент @fun — строка, описывающая подынтегральную функцию. Этс может быть либо дескриптор функции, либо объект inline (в последнем случае символ «@» в ее записи отсутствует). Обычная запись в апострофах тепер недопустима. Эта функция должна быть функцией двух переменных вид. fout=fun(inner.outer). Функция должна брать вектор inner и скаляр outer возвращать вектор fout, который является функцией, вычисленной в outer и каждом значении inner [ Функция inime(‘expr’, ‘argl’. ‘argn’) так же создает объект, но без дескриптора, ‘ехрг’ — выражеши Строки ‘argx’ —входные аргументы. При их отсутствии по умолчанию подставляется х. Если вмест ‘arg’ — скаляр, то он означает количество дополнительных переменных Р. Примеры запис; g = inline(exp); g — inline(‘t A 2’); g = inline(‘sin(2*pi*f + theta)’); g = inline(‘sin(2*pi*f + theta)’, : ‘theta’); g — inline(‘x A Pl+P2’, 2). — Примеч. ред. ];
dblquad(@fun,inmin.inmax.outmin,oiitmax,tol .trace) — передает в функцию dblquad параметры tol и trace. Смотрите справку по функции quad для получения информации о параметрах to! и trace;
dblquad(@fun,inmin,inmax,outmin,outmax.tol .trace,order) — передает параметры tol и trace для функции quad или quadl в зависимости от значения строки order. Допустимые значения для параметра order — @quad , @quadl или имя любого определенного пользователем квадратурного метода с таким же вызовом и такими же возвращаемыми параметрами, как у функций quad и quad!. (Например, при проверке старых программ можно использовать @quad8 для большей совместимости с прежними версиями MATLAB). По умолчанию (без параметра order) вызывается @quad. поскольку подинтегральные функции могут быть негладкими.
Пример: пусть m-файл integl.m описывает функцию 2*y*sin(x)+x/2*cos(y), тогда вычислить двойной интеграл от той функции можно следующим образом:
Содержание (стр. 1 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 |
1. математические модели решения различных задач вычислительной математики……………..……………………. 6
1.2 Краевые задачи для уравнений в частных производных второго порядка…………………………………………………………………………..7
1.3 Интегральные уравнения Вольтера и Фредгольма…………………. 10
2. Описание лабораторных работ, варианты и задания, контрольные вопросы…………………………..……………………12
2.1 Лабораторная работа № 1. Тема: Построение и реализация методов Рунге-Кутта решения задачи Коши………….……………………..……. 12
2.2 Лабораторная работа № 2. Тема: Построение и реализация метода Адамса решения задачи Коши……………………………………..…….…16
2.3 Лабораторная работа № 3. Тема: Решение краевой задачи методом наименьших квадратов……………..…………………………………..……19
2.4 Лабораторная работа № 4. Тема: Решение краевой задачи методом прогонки. Правило Рунге………………………………………………….…23
2.5 Лабораторная работа № 5. Тема: Решение методом сеток краевой задачи для уравнения эллиптического типа………………. ……….….26
2.6 Лабораторная работа № 6. Тема: Решение методом сеток краевой задачи для уравнения параболического типа…………….….…….……..30
2.7 Лабораторная работа № 7. Тема: Решение методом сеток краевой задачи для уравнения гиперболического типа…. …………….…….…. 34
2.8 Лабораторная работа № 8. Тема: Решение методом регуляризации интегрального уравнения Вольтера I рода…………………..…..…….…..38
2.9 Лабораторная работа № 9. Тема: Решение методом квадратур интегрального уравнения Вольтера II рода………………………….…….40
2.10 Лабораторная работа № 10. Тема: Решение методом регуляризации интегрального уравнения Фредгольма I рода………………………..……43
2.11 Лабораторная работа № 11. Тема: Решение методом квадратур интегрального уравнения Фредгольма II рода…………………. ……. 46
2.12 Лабораторная работа № 12. Тема: Решение интегрального уравнения Фредгольма II рода методом замены ядра на вырожденное ядро………………………………………….………………………….……. 49
3. Программная реализация решения лабораторных работ в среде mathcad…………………….…………………….….…52
3.1 Алгоритмы решения задач……..………………………………….…….52
3.2 Примеры решений тестовых заданий…………………………….…….56
Введение
Математика как наука возникла в связи с необходимостью решения практических задач: измерений на местности и т. д. Вследствие этого математика была численной математикой, ее целью являлось получение решения в виде числа.
Методы вычисления прикладных задач интересовали математиков. Крупнейшие представители прошлого сочетали в своих исследованиях изучение явлений природы, получение их математического описания, как иногда говорят, математической модели явления, и его исследование. Анализ усложненных моделей потребовал создания специальных методов решения задач.
Настоящее время характерно резким расширением приложений математики, во многом связанным с созданием и развитием средств вычислительной техники. В результате появления ЭВМ с программным управлением за последние несколько лет скорость выполнения арифметических операций значительно возросла. Расширение возможностей приложения математики обусловило математизацию различных разделов науки: химии, экономики, биологии, медицины, конкретных разделов техники и др. процесс математизации состоит в построении математических моделей процессов и явлений и в разработке методов их исследования.
Эти теоретические исследования оказывают большую помощь при решении конкретных задач и играют существенную роль в наблюдаемом сейчас широком распространении сферы приложений ЭВМ и математики вообще.
Одним из самых популярных компьютерных математических пакетов, позволяющий проводить разнообразные математические расчеты, является математический редактор MathCad. Пользователи MathCad – это, студенты, ученые, инженеры, разнообразные технические специалисты. Пакет MathCad мощный микрокалькулятор, позволяющий легко справляться с рутинными задачами. Сюда можно отнести решение алгебраических и дифференциальных уравнений с постоянными и переменными параметрами, анализ функций, поиск их экстремумов, численное и аналитическое дифференцирование и интегрирование, вывод таблиц и графиков при анализе найденных решений.
MathCad очень прост в использовании, в частности, из-за отсутствия необходимости сначала писать программу, реализующую те или иные математические расчеты, а потом запускать ее на выполнение. Вместо этого достаточно просто вводить математические выражения с помощью встроенного редактора формул, причем в виде, которому привыкли писать на листке бумаги, и тут же получать результат.
Работа состоит из четырех разделов.
Первый раздел называется «Математические модели решения различных задач вычислительной математики». В ней идет речь математических о моделях решения задач.
Второй раздел посвящен методическим рекомендациям, в котором идет речь о теории решения задачи Коши, решения краевых задач различными способами и о теории методов квадратур для решения интегральных уравнений Вольтера и Фредгольма.
В третьем разделе рассматривается программная реализация решения уравнений.
1. Построение математической модели решения уравнений
1.1 Задачи Коши
Для обыкновенного дифференциального уравнения первого порядка рассматривается задача Коши 
с начальным условием 
. Она задает в плоскости XOY множества интегральных кривых y=y(x, C), C – произвольная постоянная. Уравнение имеет бесконечное число решений. Начальное условие фиксирует из всего множества интегральных кривых одну проходящую через точку с координатами (x0,y0). Все методы решения задачи , делятся на две основные группы: аналитические и численные. В аналитических методах строится последовательность функции yn(x) в пределе, т. е. 
. В численных методах определяется приближенные значения функций y(x) в узлах сетки заданной в некоторой окрестности в точке x0. Численные методы делятся на одношаговые (метод Рунге-Кутта) и многошаговые (метод Адамса).
В основе схемы Рунге-Кутта построения одношаговых методов лежит соотношение 
, позволяющее при известном значении y(x) оценить y(x+h).
Интеграл приближенно заменяется квадратурной суммой:
. Таким образом, предлагается оценивать значения y(x+h) по формуле 
.
В данном методе для оценки значения y(x) в рассматриваемом узле сетки привлекается информация о значении y(x) только в одном предыдущем узле.
Таким образом, расчет yn, где yn=y(x) производится по формуле 
, где шаг h вычисляется по формуле 
.
В отличие от одношаговых методов, в многошаговом методе метода Адамса при вычислении y(x) в интересующем нас узле xn+1 используется информация о значениях y(x) в нескольких предыдущих узлах xn, xn+1, …,xn-q. Поскольку мы используем больше информации при вычислении следующего приближения, многошаговые методы обеспечивают более высокую точность, чем одношаговые. В основе построения многошаговых методах, как и в основе метода Рунге-Кутта, лежит соотношение . Интеграл заменяется квадратурной формулой 
. Расчетная формула имеет вид 
, где h вычисляется по формуле . Отметим, что для начала расчетов по формуле необходимо указать значения 
. Эти значения могут быть найдены, например, по одному из одношаговых методов. Так, Метод Эйлера дает , 0£n£q-1.
1.2 Краевые задачи для уравнений в частных производных второго порядка
Для линейного дифференциального уравнения второго порядка рассматривается краевая задача 
, с краевыми условиями 
. Методы приближенного решения краевых задач делятся на две группы: аналитические и конечноразностные. К числу аналитических методов относится метод наименьших квадратов. В рамках этого метода приближенное решение задачи ищется в виде линейной комбинации 
, где 
— некоторая система базисных функций. К конечноразностным методам относится метод прогонки. Задача отыскания функции y(x), удовлетворяющей краевым условиям заменяется задачей нахождения значений y(xk) этой функции в узлах сетки, 
. Если сетка 
достаточно “густая” (величина шага мала), то набор 
достаточно хорошо представляет искомую функцию y(x). Значения выражаются из системы линейных уравнений, полученной заменой производных в краевой задаче во внутренних узлах подходящими разностными выражениями при учете граничных условий. Это система вычисляется методом прогонки (специальный вариант метода Гаусса). Она состоит в последовательном выражении неизвестных yk через неизвестные yk+1, yk+2 и последующей подстановки одного уравнений в другое.
Окончательный процесс нахождения значений 
следующий: последовательно вычисляются 
. Этот этап расчетов называется прямым ходом прогонки. Далее получаем 
. Данный этап называется обратным ходом прогонки.
Метод сеток краевой задачи для уравнения эллиптического типа (уравнение Пуассона) заключается в поиске функции U(x, y), определенную при 
, удовлетворяющую соотношениям 
, 
, 
, 
. Уравнения , , описывают, в частности, стационарное тепловое поле в области [0,a]*[0,b]. Стационар по времени не изменяется. При этом функция U(x, y) — температура поля в точке (x, y) принадлежащая области, а функция g(x, y) описывает плотность внешних источников тепла, действующих на поле. Функция 
задает температурный режим на границе области Г.
Метод сеток краевой задачи для уравнения параболического типа (уравнение теплопроводности) заключается в поиске функции U(x, y) определенную при 
, удовлетворяющую соотношениям 
, 
, 
, 
,
.
Эти соотношения описывают, в частности, явление изменения температуры в тонком однородном стержне длины l за промежуток времени длительности T. Функция U(x, t) задает температуру стержня в точке с абсциссой x в момент t (левый конец стержня находится в точке x=0, правый в точке x=l). Функция 
определяет плотность внешних источников тепла, приложенных к точке x в момент t, 
— задает начальную температуру в точке 
стержня, функции 
— описывают температурные режимы, поддерживаемые на концах стержня, a2 – коэффициент теплопроводности стержня.
Метод сеток краевой задачи для уравнения гиперболического типа (уравнение колебания струны) заключается в поиске функции U(x, y) определенную при , удовлетворяющую соотношениям 
, 
, ,
. Эти соотношения описывают, в частности, процесс поперечных колебаний тонкой однородной струны длины l, левый конец которой располагается в момент времени t в точке 
, а правый — в точке 
.
При этом функция U(x, t) – описывает отклонение от положения равновесия точки с абсциссой x в момент времени t. Функция g(x, t) характеризует плотность внешних сил, действующих в момент времени t на точку струны с абсциссой x, a2 – коэффициент упругости струны. Функции 
и определяют соответственно начальное отклонение струны от положения равновесия и начальные скорости точек струны, а функции описывают колебания концов струны. Если 
, то струна закреплена.
1.3 Интегральные уравнения Вольтера и Фредгольма
Интегральные уравнения Вольтера делятся на 2 типа: первого и второго рода.
Линейное интегральное уравнение Вольтера первого рода имеет вид: 
. Если K (a, a) не равно 0, F (a) = 0 и если функции F (s), K (s, t) имеют производные F ‘ (s), K ‘ s (s, t), непрерывные в интервале (a, b), заключенном в интервале интегрирования, внутри которого K(s, t) не обращается в нуль, то уравнение Вольтера первого рода допускает в интервале (a, b) непрерывное и единственное решение. Представленная процедура решает уравнение методом квадратурных формул. Вычисление интеграла производится по формуле трапеций с постоянным шагом h, где шаг определяется, как h=(b-a)/2.
Линейное интегральное уравнение Вольтера второго рода имеет вид: 
, независимые переменные s, t изменяются на промежутке [a, b], ядро K(s, t) непрерывно внутри и на сторонах треугольника, ограниченного прямыми t =a, s =b, t = s. Функция f(t) на [a, b] непрерывна.
Уравнение данного типа решается с помощью метода квадратурных формул, суть которого состоит в замене интегрального уравнения аппроксимирующей системой алгебраических уравнений относительно дискретных значений искомой функции и решении этой системы. В основе такой замены лежит приближение интеграла квадратурными формулами. Применение формулы трапеций с постоянным шагом h приводит к рекуррентной формуле.
Неоднородное линейное интегральное уравнение Фредгольма первого рода имеет вид: 
, где ядро определено в квадрате V = [a, b] * [a, b]. Для уравнения Фредгольма первого рода задается последовательность регуляризующих параметров 
. Решение уравнений данного типа решается с помощью метода квадратурных формул.
Неоднородное линейное интегральное уравнение Фредгольма второго рода имеет вид: 
, где ядро определено в квадрате V = [a, b] * [a, b]. Кроме того, полагается, что ядро непрерывно в V. При b= 1, используя квадратурную формулу трапеций с постоянным шагом h, который определяется, как h=(b-a)/2. Решение уравнений данного типа решается с помощью метода квадратурных формул и метода Гаусса.
Для уравнения Фредгольма второго рода существует еще один способ решения. Это метод замены ядра на вырожденное ядро. Ядро K(s, t) называется вырожденным, если существует система линейно независимых функций 
, где 
, такие, что 
.
2. Описание лабораторных работ, варианты и
задания, контрольные вопросы
2.1 Лабораторная работа № 1
Построение и реализация методов Рунге-Кутта решения
задачи Коши
Цель работы: Научиться строить в рамках схемы Рунге-Кутта создания одношаговых методов методы второго порядка точности и использовать их для решения задачи Коши.
Рассматривается задача Коши для обыкновенного дифференциального уравнения первого порядка:
(1)
В основе одношаговых методов лежит соотношение: (2)
Интеграл в формуле (2) приближенно заменим квадратурной суммой: (3)
Таким образом, значения y(x+h) оцениваются по формуле: 
(4)
Функции 
составляются по формулам
(5)
где общее число параметров 
определяется целочисленным параметром q>0.
Для оптимального выбора параметров, при котором обеспечивается наибольшая точность приближенного равенства, составляется функция невязки, т. е. разность между его левой и правой частью. 
(6)
Находим производные 
. Положив в производных h=0, запишем уравнения 
и, исходя из них, выписываем условия на параметры 
, обеспечивающие выполнение этих соотношений.
Численная реализация осуществляется следующим образом. На отрезке [x0,X] определяем равномерную сетку 
, так что 
, 
.
Обозначим за 
искомое приближенное значение функции 
в точке 
.
Расчет проводится по формуле:
(7)
(8)
Выпишем схемы нахождения 
, отвечающие значениям A0=0 (усовершенствованный метод Эйлера), т. е.
или 
(9)
и A0=0.5 (метод Эйлера-Коши), т. е. 
или 
(10)
Вычислим последовательно приближенное решение по двум схемам.
1. Сформулируйте задачу Коши для дифференциального уравнения первого порядка.
2. Изложите схему построения методов Рунге-Кутта.
3. В чем заключается метод Эйлера решения задачи Коши?
4. С какой целью величину s стремятся сделать наибольшей?
Задание к лабораторной работе
1. Положив в описанной выше схеме Рунге-Кутта q=1, выписать для этого случая функцию j(h).
2. Привлекая при необходимости основное уравнение и правило дифференцирования сложных функций, найти производные j’(h), j”(h).
3. Положив в производных h=0, записать уравнения j’(0)=0, j”(0)=0 и исходя из них, выписать условия на параметры a1,b10,A0,A1, обеспечивающие выполнение этих соотношений. Какой порядок точности при этом гарантируется?
4. Выписать конкретные схемы и соответствующие им методы нахождения , отвечающие значениям A0=0 (усовершенствованный метод Эйлера) и A0=0.5 (метод Эйлера-Коши)
5. Построенными в пункте 4 методами провести расчет значений для задачи Коши (см. варианты заданий) при N=5 на отрезке [0,1].
И. О. Арушанян. Практикум на ЭВМ Численное решение интегральных уравнений методом квадратур. МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ им. М.В.
- Филипп Недобров 5 лет назад Просмотров:
1 МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ им. М.В.ЛОМОНОСОВА Механико математический факультет Кафедра вычислительной математики И. О. Арушанян Практикум на ЭВМ Численное решение интегральных уравнений методом квадратур Третье издание, дополненное Москва, 1
2 И О. Арушанян ЧИСЛЕННОЕ РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ МЕТОДОМ КВАДРАТУР ОГЛАВЛЕНИЕ Введение Численное интегрирование Квадратурные формулы интерполяционного типа Элементарные формулы трапеций, средних прямоугольников и Симпсона Составные формулы трапеций, средних прямоугольников и Симпсона Построение формул Ньютона Котеса методом неопределенных коэффициентов Квадратурные формулы Гаусса Правило Рунге практической оценки погрешности квадратурных формул Процесс Эйткена оценки фактической точности квадратурной формулы Способы построения практическихалгоритмов численного интегрирования. Адаптивные алгоритмы Простейший неадаптивный) алгоритм Модификация простейшего алгоритма Адаптивный алгоритм последовательного передвижения слева-направо Адаптивный алгоритм с контролем точности по глобальной ошибке Интегральные уравнения Фредгольма второго рода Метод квадратур решения интегральных уравнений Фредгольма второго рода Сходимость метода квадратур. 43
3 .1.. Практический алгоритм численной реализации метода квадратур Метод последовательных приближений Первый алгоритм численной реализации метода последовательных приближений Второй алгоритм численной реализации метода последовательных приближений Интегральные уравнения Вольтерра второго рода Метод квадратур решения интегральных уравнений Вольтерра второго рода Сходимость метода квадратур Построение приближенного решения в виде непрерывной функции Способы построения квадратурных формул для решения уравнений Вольтерра второго рода Практический алгоритм построения приближенного решения с заданной точностью Варианты выполнения задания. Содержание отчета Тестовые задачи для отладки программ Литература
4 ЧИСЛЕННОЕ РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ МЕТОДОМ КВАДРАТУР Введение Данное учебное пособие посвящено рассмотрению метода квадратур для решения линейных интегральных уравнений второго рода, предлагаемого для практической реализации на ЭВМ при выполнении заданий студенческого практикума на механико-математическом факультете Московского университета. В пособии рассматриваются два типа интегральных уравнений. Это интегральные уравнения Фредгольма второго рода b ux) Kx, s)us)ds = fx), x [, b], ) и интегральные уравнения Вольтерра второго рода ux) x Kx, s)us)ds = fx), x [, b]. ) Здесь ux) искомая функция с областью определения [, b]. Заданные функции Kx, s) и fx) называются соответственно ядром и правой частью интегрального уравнения. Формально уравнение **) является частным случаем уравнения *), если ядро уравнения отвечает условию Kx, s) при s > x. Однако это свойство функции K имеет настолько глубокие следствия, что делает теории интегральных уравнений **) и *) принципиально различными. В рамках пособия имеет смысл остановиться на том, какое влияние оказывают эти отличительные особенности на методы численного решения интегральных уравнений. Из всего многообразия методов численного решения интегральных уравнений вида *) и **) в пособии рассматривается только метод квадратур и некоторые его модификации. Входящие в уравнения интегралы заменяются квадратурными суммами, а полученные конечные соотношения могут быть как вспомогательными, так и имеющими самостоятельный характер в качестве окончательных расчетных выражений. 6
5 В уравнениях Вольтерра **) значение искомой функции u в точке x определяется ее значениями в предшествующих точках s x не влияют на ux). Для приближенного решения уравнения на отрезке [, b] берут сетку из точек s 6 1. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ Пусть требуется вычислить значение определенного интеграла I = b fx)dx, где функция fx) непрерывна на отрезке [, b]. Числа и b называют пределами интегрирования; они могут быть как конечными, так и бесконечными тогда интеграл называется несобственным). Как известно, через элементарные функции интегралы выражаются далеко не всегда. По этой и другим причинам для их вычисления применяют численные методы, основанные на замене fx) такой аппроксимирующей функцией, чтобы интеграл от нее вычислялся в элементарных функциях достаточно просто Квадратурные формулы интерполяционного типа В качестве аппроксимирующих функций возьмем интерполяционные многочлены Лагранжа L n x). Тогда искомый интеграл заменяется линейной комбинацией значений подынтегральной функции fx): I = b fx)dx = n c i fx i ) + R = n c i f i + R. 1) Выписанное соотношение называется квадратурной формулой или просто квадратурой), в которой величины x i называют узлами, c i весами, а R погрешностью остаточным членом). Таким образом, интеграл приближенно заменяется суммой, похожей на интегральную сумму, причем узлы и веса не зависят от fx). Рассмотрим квадратуру 1) более подробно. Пусть узлы x i образуют равномерную сетку с шагом h: x i+1 = x i + h, i = 1. n. Если пределы интегрирования и b входят в состав сетки, то h = b )/n 1) и 8 x 1 =, x i = x 1 + i 1)h, x n = b.
7 В этом случае формула 1) называется формулой замкнутого типа и имеет по крайней мере два узла. Исходный отрезок интегрирования разбивается на n 1 подотрезков длины h. Если и b не входят в состав сетки, то h = b )/n + 1) и x i = +ih. Тогда формула 1) называется формулой открытого типа и может иметь один узел. Количество подотрезков равно n + 1. Если либо, либо b включены в состав сетки, то соответствующие квадратуры носят название полуоткрытых или полузамкнутых). Теперь заменим fx) на многочлен Лагранжа L n x), интерполирующий fx) в точках x i, f i ) на отрезке [, b]: fx) = L n x) = n f i l i x) + ω nx) n! f n) ξ), ξ [, b], где ω n x) = x x 1 ). x x n ) и l i x) = j=1 j i = x x j x i x j = x x 1 ). x x i 1 )x x i+1 ). x x n ) x i x 1 ). x i x i 1 )x i x i+1 ). x i x n ). Функции l i x) называют фундаментальными многочленами Лагранжа. Подставив выписанное приближенное представление fx) в 1), получим где I = n b = b ) l i x)dx f i + n c i f i + R, b ω n x) n! f n) ξ)dx = ) c i = 1 b l i x)dx, R = 1 b ω n x)f n) ξ)dx. b n! 9
8 Если сетка
9 Главный член погрешности формулы Ньютона Котеса с n узлами при условии достаточной гладкости fx) имеет порядок O h [n 1)/]+3), где [ ] целая часть числа. Порядок по h главного члена погрешности называется порядком точности сходимости) квадратурной формулы. Для формул замкнутого типа коэффициенты Котеса c i положительны при 1 n 8, а при n = 9 и n 11 среди них есть отрицательные, что приводит к увеличению ошибок, содержащихся в fx). Действительно, пусть ошибка задания функции fx) в каждом узле сетки оценивается сверху по модулю некоторой величиной ε. Погрешность, которая может получиться в сумме c i f i, оценивается величиной ε c i. Поскольку ci = 1, то наличие отрицательных c i приводит к увеличению c i. Коэффициент увеличения ошибок иллюстрируется следующими цифрами: ci 1.45, n = 9; ci 3.1, n = 11; ci 8.3, n = 15; ci 56, n =. Значения c i при больших n быстро растут по абсолютной величине, а c i будет большой и быстро возрастающей величиной. Коэффициент увеличения ошибок становится неприемлемым, а соответствующие формулы непригодными для расчетов. Для формул открытого типа коэффициенты Котеса положительны при n = 1,, 4, а при остальных n среди них есть отрицательные. 1.. Элементарные формулы трапеций, средних прямоугольников и Симпсона Рассмотрим первые три формулы Ньютона Котеса. Сначала приблизим fx) на [, b] многочленом Лагранжа L x) с узлами x 1 = и x = b. Это означает, что вместо кривой fx) мы взяли многочлен первой степени, проходящий через точки, f)) и b, fb)). Теперь искомый интеграл, равный площади криволинейной фигуры, заменим на площадь трапеции с осно- 11
10 ваниями f) и fb) и высотой h = b : I T = h f) + fb) = b f) + fb) ). 3) Мы получили квадратурную формулу трапеций, которую можно также получить из ) при n = с сеткой для формул замкнутого типа. Заметим, что алгебраический порядок точности этой формулы равен единице, т.к. середина отрезка [, b] не входит в состав сетки. Если на [, b] взять единственный узел квадратурной формулы, то fx) аппроксимируется многочленом Лагранжа L 1 x), т.е. многочленом нулевой степени. Возьмем в качестве этого узла середину отрезка x = + b)/. Тогда получим формулу средних прямоугольников I P = h f x). 4) Геометрический смысл этой формулы состоит в том, что площадь криволинейной фигуры заменяется на площадь прямоугольника с основанием h = b и высотой f x). Ту же самую формулу можно получить из ) при n = 1 с сеткой для формул открытого типа. Алгебраический порядок формулы средних прямоугольников равен единице, поскольку середина отрезка интегрирования входит в состав узлов сетки. Теперь получим выражения для остаточных членов R T = I T и R P = I P. Для этого разложим fx) в ряд Тейлора относительно точки x = + b)/ в предположении о достаточной гладкости функции fx): fx) = f x) + x x)f x x) x) + f x) + x x)3 + f x x)4 x) + f IV x) Воспользовавшись этим разложением, получим представление остаточного члена формулы средних прямоугольников: 5) 1 I = hf x) + h3 4 f x) + h5 19 fiv x) + = P + R P, 6)
11 поскольку h, j=;, j=1; b h 3 x x) j dx = 1, j=;, j=3; h 5 8, j=4. Подставим в 5) x = и x = b и учтем, что x = h/ и b x = h/: f) = f x) h f x) + h 8 f x) h3 48 f x) + h4 384 fiv x) +, fb) = f x) + h f x) + h 8 f x) + h3 48 f x) + h4 384 fiv x) +. Сложим эти два равенства: f) + fb) Отсюда получим hf x) = h = f x) + h 8 f x) + h4 384 fiv x) +. f) + fb) h3 8 f x) h5 384 fiv x) +. Подставим это выражение вместо hf x) в 6): f) + fb) I = h h3 1 f x) h5 48 fiv x) + = T + R T. 7) Итак, главные члены погрешности в формулах средних прямоугольников и трапеций равны h3 4 f x) и h3 1 f x) и имеют противоположные знаки. Это означает, что точное значение интеграла лежит в вилке между ними. Объединяя 6) и 7), можно записать напомним, что здесь h = b ): I = + h3 4 f x) + h5 19 fiv x) +, I = T h3 1 f x) h5 48 fiv x) +. 13
12 Умножим первое равенство на /3, а второе на 1/3 и сложим: I = T h5 88 fiv x) + = S h5 88 fiv x) +. Мы видим, что новая формула S, называемая формулой Симпсона или формулой парабол), имеет вид S = T = h ) ) + b f) + 4f + fb), h = b. 8) 6 Главный член погрешности этой формулы равен h5 88 fiv x). Отметим важное обстоятельство: из самого вывода этой формулы видно, что ее остаточный член R S на равномерной сетке имеет разложение по нечетным степеням h = b, начиная с h 5. Следовательно, формула Симпсона точна для многочленов третьей степени. Коэффициенты формулы Симпсона и оценку остаточного члена можно вывести из ) при n = 3 для сетки замкнутого типа. Из этого построения следует, что полученная формула должна быть точна для многочленов второй степени, однако она обладает повышенной точностью в силу своей симметрии. Изменим запись формулы Симпсона 8), рассматривая ее как частный случай формулы Ньютона Котеса для равномерной сетки из трех узлов с шагом h = b )/: S = h ) ) + b f) + 4f + fb) Составные формулы трапеций, средних прямоугольников и Симпсона В общем случае длина отрезка [, b] не мала, а потому остаточный член в рассматриваемых формулах может быть велик. Для повышения точности на отрезке интегрирования вводят достаточно густую сетку = x 1 13 интеграл I разбивают на сумму интегралов I i по каждому элементарному подотрезку, которые вычисляются по формулам из п. 1.. Таким образом, получают составные, или обобщенные, квадратурные формулы. В нашем случае это: составная формула трапеций 1 n 1 1 n 1 n 1 I = T i + Ri T = 1 h 3 if xi + x i+1 n 1 h i f i + f i+1 ) ) 1 n 1 48 составная формула средних прямоугольников + 1 n 1 4 I = n 1 R n 1 i + h 3 if xi + x i+1 = i ) h 5 if IV xi + x i+1 + ; n 1 ) xi + x i+1 h i f + ) составная формула Симпсона n 1 n 1 I = S i + Ri S = n 1 88 n 1 n 1 xi + x i+1 h i f i + 4f h 5 if IV xi + x i+1 ) h 5 if IV xi + x i+1 + ; ) +. ) + f i+1 ) На равномерной сетке остаточные члены этих квадратурных формул могут быть представлены следующим образом отбрасываем члены, содержащие более высокие степени h): R T h n 1 ) hf xi + x b i+1 h f x)dx;
14 R h n 1 4 ) hf xi + x b i+1 h f x)dx; 4 R S h4 n 1 ) hf IV xi + x b i+1 h4 f IV x)dx Приведенные оценки являются асимптотическими, т.е. выполняются при h с точностью до членов более высокого порядка малости. Но для справедливости этих оценок необходимо существование непрерывных производных подынтегральной функции соответствующих порядков. Если эти производные кусочно-непрерывны, то можно сделать только мажорантные оценки: R T b ) 1 b ) h h M, R S b ) M, R 4 88 h4 M 4, M = mx [,b] f x), M 4 = mx [,b] fiv x) Построение формул Ньютона Котеса методом неопределенных коэффициентов Для повышения точности интегрирования можно увеличивать число точек n, по которым подынтегральная функция аппроксимируется интерполяционным многочленом Лагранжа. В этом случае коэффициенты c i и остаточный член R определяются из ). Более наглядным способом мы построили формулы замкнутого типа для n = и n = 3 и формулу открытого типа для n = 1. Рассмотрим другой способ построения квадратурных формул, называемый методом неопределенных коэффициентов. Будем рассматривать только формулы замкнутого типа. Пусть n = 4. Формула не будет симметричной, т.к. середина отрезка не входит в состав сетки. Построим формулу вида 16 I = b fx)dx c 1 fx 1 ) + c fx ) + c 3 fx 3 ) + c 4 fx 4 ),
15 где x 1 =, x = + b 3, x 3 = + b 3, x 4 = b. Коэффициенты c i будем подбирать так, чтобы эта формула была точна для многочленов как можно более высокой степени. Для упрощения выкладок проведем стандартную замену переменных x = b + + b в результате которой получим b fx)dx = b t, 1 t 1, x b, 1 1 f xt) ) dt = b 1 1 gt) dt. Теперь, с учетом проведенной замены, исходная задача свелась к поиску таких коэффициентов d i, чтобы квадратурная формула 1 1 gt)dt d 1 g 1) + d g 1/3) + d 3 g1/3) + d 4 g1) была точна для многочленов наиболее высокой степени. Погрешность квадратуры имеет вид Rg) = 1 1 gt)dt d 1 g 1) + d g 1/3) + d 3 g1/3) + d 4 g1) ). Подставим в это выражение многочлен gt) = m j t j степени m: Rg) = n j R t j). j= Подбором d i мы попытаемся добиться выполнения равенств R1) =, Rt) =. Rt m ) = j= 17
16 при возможно большем значении m. Подставим в эти равенства последовательно gt) 1, gt) t, gt) t, gt) t 3. Получим систему из четырех линейных уравнений, решение которой дает следующие значения коэффициентов квадратурной формулы: d 1 = d 4 = 1 4, d = d 3 = 3 4. Проверкой убеждаемся, что построенная квадратурная формула не будет точна для gt) t 4. Учитывая, что c i = d i b )/ и b = 3h, получим искомую квадратурную формулу с введенными выше узлами x i : b fx)dx 3 8 h f 1 + 3f + 3f 3 + f 4 ). 9) Эту квадратуру называют правилом или формулой) трех восьмых. Поскольку она точна для многочленов третьей степени, то ее остаточный член имеет порядок Oh 5 ) т.е. тот же, что и остаточный член формулы Симпсона), однако раскладывается в ряд Тейлора по последовательным степеням h. Ту же формулу можно получить из ) при n = 4. Погрешность формулы 9) представляется в виде 3h 5 f IV ξ)/8, ξ [, b]. Составная формула трех восьмых может быть построена разбиением [, b] на элементарные подотрезки с последующим применением 9) на каждом из них. Мы же построим ее в несколько другом виде. Возьмем число элементарных подотрезков кратным трем, т.е. равным 3m, m = 1. Тогда число узлов полученной сетки n = 3m + 1, а ее шаг h = b )/n 1) = b )/3m. Возьмем строенный отрезок [+kh, +k +3)h], k =, 3, 6. и применим на нем правило 9): где +k+3)h +kh fx)dx = 3 8 h f 1 + 3f + 3f 3 + f 4 ) + R k+1, 18 R k+1 = 3h5 8 fiv ξ k+1 ), ξ k+1 [ + kh, + k + 3)h].
17 Если эти равенства расписать для всех остальных строенных подотрезков и сложить их почленно, то получим составную формулу трех восьмых: b fx)dx = 3h 8 [ f1 + f n ) + f 4 + f f n 3 ) + + 3f + f 3 + f 5 + f f n + f n 1 ) ] + R, где погрешность R ведет себя следующим образом: R = h4 [ 3h f IV ξ 1 ) + + f IV ξ m/3 ) ]) b h4 f IV x)dx. 8 8 Мажорантная оценка имеет вид R b ) 8 h 4 M 4, M 4 = mx f IV x). [,b] Хотя формула Симпсона по точности и количеству вычислений значений подынтегральной функции предпочтительнее, правило трех восьмых имеет самостоятельное значение, т.к. оно может быть использовано в случае таблично заданной функции и нечетного числа элементарных отрезков, когда формула Симпсона неприменима. Возьмем теперь n = 5, h = b )/4. В этом случае квадратурная формула будет симметрична, т.к. середина отрезка входит в состав сетки; следовательно, она будет точна не только для многочленов четвертой степени, но и пятой. Применяя описанный выше метод неопределенных коэффициентов, получим следующую формулу ее иногда называют формулой Боде): b b ) fx)dx 7 45 f f f f ) 45 f 5 = 14 =h 45 f f f f ) 45 f 5. 19
18 Главный член ее погрешности равен h7 f V I ξ), ξ [, b], а остаточный член разлагается по нечетным степеням h, начиная с h 7. Может быть построена составная формула Боде с главным членом погрешности Oh 6 ) Квадратурные формулы Гаусса При построении квадратурных формул Гаусса важную роль играют ортогональные многочлены Лежандра, имеющие вид: P n x) = 1 n n! d n dx n [ x 1) n], n =, 1. Эти многочлены обладают следующими свойствами: 1) P n 1) = 1, P n 1) = 1) n, n =, 1. ; ) 1 1 P n x)q k x)dx =, k 19 Поставим задачу определения узлов t 1, t. t n на [ 1, 1] и коэффициентов c 1, c. c n, чтобы квадратурная формула 1 1 ft)dt n c i ft i ) была точной для многочленов наиболее высокой степени. Формулы, обладающие таким свойством, называются квадратурными формулами квадратурами) Гаусса. Другое название квадратурные формулы наивысшей алгебраической степени точности. Поскольку в квадратуре Гаусса мы имеем n свободных параметров t i и c i, i = 1. n, а многочлен степени n 1 определяется n коэффициентами, то можно подобрать эти параметры так, чтобы наивысшая степень многочлена в общем случае равнялась N = n 1. Для того чтобы квадратурная формула была точна для многочленов степени до n 1 включительно, необходимо и достаточно, чтобы она была точна для одночленов ft) 1, t, t. t n 1. Будем подбирать параметры t i и c i методом неопределенных коэффициентов, который мы использовали ранее для построения формул Ньютона Котеса. Получим систему n уравнений с n неизвестными: n c i =, n c i t i =. n c i t n i = n c i t n 1 i =. n 1, 1) 1
20 Эта система нелинейная, поэтому ее решение затруднено уже при небольших значениях n. Кроме того, нет никакой гарантии, что она вообще разрешима, или что ее решения t i вещественны и принадлежат отрезку [ 1, 1]. Докажем разрешимость системы 1). Рассмотрим семейство многочленов вида f k t) = t k P n t), k =, 1. n 1, где P n t) многочлен Лежандра. Так как степени многочленов f k t) не превосходят n 1, то, если t i и c i удовлетворяют системе 1), должны быть выполнены равенства 1 1 t k P n t)dt = n c i t k i P nt i ), k =, 1. n 1. В силу свойства ортогональности многочленов Лежандра справедливы равенства Следовательно, 1 1 t k P n t)dt = k 21 Осталось показать, что построенная квадратурная формула точна для всех многочленов степени до n 1 включительно. Действительно, представим произвольный многочлен Q n 1 t) степени n 1 в виде Q n 1 t) = G n 1 t)p n t) + F n 1 t), где G n 1 и F n 1 многочлены степени n 1. Предложенная квадратурная формула по своему построению точна для каждого из слагаемых в этом разложении, следовательно, точна и для произвольного многочлена степени не выше n 1. В случае применения квадратуры Гаусса для вычисления интеграла на произвольном отрезке [, b] делаем замену переменных x = b + + b t, в результате которой получим b fx)dx = b 1 1 b + f + b ) t dt. Последний интеграл заменим квадратурной формулой Гаусса: b fx)dx b n c i fx i ), где x i = b + + b t i, i = 1. n, а t i корни многочлена Лежандра P n t) на [ 1, 1]. Остаточный член формулы Гаусса с n узлами имеет вид R n = b )n+1 n!) 4 f n) ξ) [n)!] 3 n + 1) с учетом формулы Стирлинга) b.5 n ) n b f n) ξ), ξ [, b]. 3n 3
22 В частности, R R ) 5 b f 4) ξ), ) 7 b f 6) ξ). Кроме того, имеем t i = t n i+1 в силу свойств корней многочлена Лежандра) и c i = c n i+1 в силу равенства коэффициентов при симметричных узлах). Могут быть построены составные формулы Гаусса, если отрезок интегрирования разбить на подотрезки и на каждом из них применить формулу Гаусса. Однако в отличие от составных формул Ньютона Котеса замкнутого типа, в которых можно экономить одно обращение к подынтегральной функции на каждой граничной точке подотрезка кроме концов всего отрезка интегрирования), в составных формулах Гаусса такой возможности нет Правило Рунге практической оценки погрешности квадратурных формул Из п следует, что чем выше степень многочлена Лагранжа L n x), аппроксимирующего заданную подынтегральную функцию, тем выше точность соответствующей квадратуры. Это верно для достаточно малых длин отрезков интегрирования. Кроме того, не следует забывать, что для аппроксимации, как правило, используют L n x) для n, не б ольших 4 или 5. Поэтому применяется аппроксимация не сразу на всем отрезке, а кусочно-полиномиальная аппроксимация многочленами невысокой степени, что приводит к построению составных квадратур. При этом возможны два способа: либо берут достаточно густую равномерную сетку и на ней строят составную формулу; либо разбивают отрезок на подотрезки и затем на каждом из них применяют элементарную квадратуру с одновременным суммированием полученных приближений интеграла на этих подотрезках. 4
23 Шаг сетки и длины подотрезков следует подбирать из того требования, чтобы значение интеграла вычислялось с некоторой заранее предписанной точностью. Для оценки достигнутой при вычислении интеграла точности мы имеем пока только асимптотические или мажорантные оценки остаточных членов квадратурных формул, которые либо трудно использовать на практике, либо дают излишне малые значения для шага интегрирования и длины подотрезков. Поэтому применяется другой практически эффективный и легко реализуемый способ контроля точности интегрирования, основанный на оценке главного члена погрешности квадратуры при помощи правила Рунге. Этот метод называют еще методом двойного пересчета или экстраполяцией по Ричардсону. Пусть на [, b] взята равномерная сетка
24 Равенство 13) называют первой формулой Рунге. Таким образом, можно сформулировать простейший алгоритм вычисления интеграла с заданной точностью ε по выбранной квадратурной формуле: если δ = ch p ε, то интеграл вычислен с заданной точностью, если δ > ε, то шаг h еще раз делится пополам и процедура повторяется. Подставим теперь 13) в 11). В результате получим новую квадратурную формулу I h,h/ с главным членом погрешности порядка h p+1, а не h p, т.е. вновь полученная формула будет иметь порядок точности на единицу больше, чем первоначальная формула I h : I = I h + I h/ I h 1 > << p +c 1 h p+1 + O h p+). >I h,h/ Выписанное представление интеграла носит название второй формулы Рунге. Таким образом, мы описали еще один способ построения квадратурных формул, который может быть использован наряду с методом неопределенных коэффициентов и аппарата интерполирования. Поскольку можно ожидать, что приближение I h/ более точно, чем I h, то разумно в качестве нового приближения брать I = I h/ + I h/ I h p +c h p+1 + O h p+), 14) 1 > <<>I h,h/ которое получается, если в 1) подставить оценку ) p h c I h/ I h p 1 Повторив процесс с вдвое меньшим шагом, получим формулу с главным членом погрешности порядка h p+ и т.д. Таким образом, мы получили не только способ контроля точности при вычислении интеграла, дающий возможность выбора надлежащей величины шага h, но и простой метод построения все более точных квадратурных формул без явного выписывания их в виде квадратурной суммы с коэффициентами 6
25 Котеса). В качестве исходной формулы можно взять простую формулу невысокой точности например, трапеций или средних прямоугольников). Покажем, что операция построения формулы I h,h/ носящей имя Ричардсона) есть операция экстраполирования. Для этого надо показать, что, если I h I h/, то I h,h/ всегда лежит вне отрезка с границами I h и I h/. Действительно, если I h/ > I h, то I h,h/ = I h/ + I h/ I h p 1 т.к. p 1. Если I h/ I h/, I h,h/ = I h/ I h I h/ p 1 26 у которой остаточный член раскладывается также по четным степеням, но начиная с h 4 : I = T h/,1 + b h 4 + b 3 h b s h s + O h s+). Новая формула T h/,1 имеет порядок точности, превышающий на два порядок точности формулы трапеций, т.е. она точна для многочленов третьей степени. Покажем, что новая формула T h/,1 есть формула Симпсона, записанная в неявном виде, т.е. без непосредственного выписывания коэффициентов Котеса. Для простоты вывода будем полагать, что h = b и формула трапеций строится по двум узлам. Тогда T h, = h f 1 + f ), T h/, = h 4 f 1 + f 1/ + f ), T h/,1 = h 4 f 1 + f 1/ + f ) h 3 4 f 1 + f 1/ + f ) h ) f 1 + f ) = = h 6 f 1 + 4f 1/ + f ) = S. Получили формулу Симпсона, выписанную по сетке с тремя узлами. Теперь мы можем применить правило 14) уже к формуле Симпсона T h/,1, использовав уже вычисленное T h/4,1 : T h/4, = T h/4,1 + T h/4,1 T h/, Здесь в знаменателе двойка возводится в четвертую степень, т.к. при вычислении T h/4, мы исключили член b h 4 в разложении по степеням h остаточного члена формулы T h/,1. В результате для новой формулы T h/4, остаточный член разлагается по четным степеням h, начиная с h 6 : I = T h/4, + 3 h s h s + O h s+). Следовательно, алгебраический порядок точности формулы T h/4, превышает порядок точности формулы Симпсона на два 8
27 и равен пяти т.е. она точна для многочленов пятой степени). Можно показать, что она совпадает с ранее выписанной формулой Боде, которая может быть получена методом неопределенных коэффициентов на сетке с пятью узлами. Если мы применим правило Рунге к формуле Боде T h/4,, то получим формулу по девяти узлам, имеющую седьмой порядок точности; в разложении остаточного члена этой формулы присутствуют четные степени h, начиная с восьмой. С каждым следующим применением правила Рунге к вновь полученным формулам мы будем получать формулы с порядком точности 9, 11 и т.д. Отметим, что, начиная с формулы, построенной по 14) на основе формулы Боде, порядок точности будет меньше, чем если бы эти формулы строились в качестве формул Ньютона Котеса, т.е. как формулы интерполяционного типа. Например, для n = 9 формула Ньютона Котеса имеет девятый порядок точности, а не седьмой, как формула, полученная из формулы Боде по 14). Поэтому начиная с этого момента по второму правилу Рунге нельзя построить формулы Ньютона Котеса это будут уже другие формулы, не являющиеся точными для многочленов наиболее высокой степени Процесс Эйткена оценки фактической точности квадратурной формулы У всех рассмотренных квадратурных формул остаточный член можно разложить в ряд по степеням шага сетки. Следовательно, к ним применим метод Рунге при этом требуется, чтобы был заранее известен порядок точности исходной формулы). Кроме того, разложение остаточного члена проводится при условии достаточной гладкости подынтегральной функции. Если же функция не обладает требуемой гладкостью, то это разложение уже не имеет смысла, т.е. нам уже не известен фактический реальный) порядок точности формулы. Рассмотрим процесс Эйткена, которой на основе повторных просчетов на нескольких сетках дает возможность: определить фактический порядок точности p квадратурной формулы для заданной подынтегральной функции; 9
28 уточнить результат, полученный на исходной сетке. В упрощенном виде процесс Эйткена можно описать следующим образом. Выберем три сетки с шагами h 1 = h, h = h/, h 3 = h/4. Вычислим приближения I h, I h/ и I h/4 к интегралу I по выбранной квадратурной формуле. Тогда, если учитывать только главный член погрешности, имеем три уравнения для определения I, и p, где p фактический, заранее неизвестный порядок точности формулы для данной подынтегральной функции: I = I h + ch p, I = I h/ + 1 p chp, I = I h/ p chp, в которой значения I, c и p неизвестны. Из первого и второго уравнений имеем ch p 1 1 p ) = I h/ I h. Из второго и третьего уравнений получим 1 1 p chp 1 ) p = I h/4 I h/. Из последних двух равенств получаем уравнение для определения p: p = I h/ I h I h/4 I h/. Оценка для главного члена погрешности имеет вид Ih/ I h ) ch p = I h/ I h I h/4. Полученную оценку можно использовать для уточнения I h. 3
29 Пример 1. Пусть вычисляется следующий интеграл методом трапеций: 1 x dx. Тогда для этого интеграла фактический порядок точности p будет равен 1/. Пример. Пусть вычисляется следующий интеграл методом трапеций: 1 n xdx. Тогда для этого интеграла фактический порядок точности p будет равен n + 1)/n Способы построения практических алгоритмов численного интегрирования. Адаптивные алгоритмы Ранее мы рассмотрели различные квадратурные формулы и способ Рунге контроля достигнутой при их применении точности, однако оставили в стороне вопрос построения практически пригодных алгоритмов. Всегда можно подобрать такую подынтегральную функцию fx), для которой любая заранее выбранная программа численного интегрирования дает совершенно неверные результаты. Сказанное иллюстрирует следующий простейший пример. Возьмем fx) 1 и вычислим интеграл по данной программе. Запомним выбранные этой программой узлы интегрирования x i и доопределим функцию fx) следующим образом: fx i ) = 1, fx) = A 1, x x i. Очевидно, что при повторном запуске для видоизмененной функции программа даст прежний результат, хотя верный результат может значительно отличаться от вычисленного при надлежащем задании A. Таким образом, при построении практических алгоритмов класс подобных примеров должен быть максимально сужен, насколько это возможно без неоправданного усложнения логики или потери эффективности на распространенных типах задач. 31
30 Рассмотрим несколько алгоритмов такого рода, в которых для контроля достижения предписанной точности применяется автоматический выбор шага интегрирования. При этом будем учитывать, что б ольшая часть машинного времени в реальных расчетах тратится на вычисление подынтегральной функции. Поэтому программа считается тем эффективней, чем меньше таких вычислений она производит для достижения заданной точности Простейший неадаптивный) алгоритм Зададим на отрезке интегрирования n узлов и вычислим по выбранной квадратурной формуле приближенное значение I n интеграла I по этим узлам. Затем увеличим число узлов вдвое и вычислим I n. По первому правилу Рунге вычислим оценку погрешности ошибки, которая, конечно, не учитывает погрешность суммирования R Σ, а дает лишь оценку главного члена погрешности самой формулы, т.е. метода интегрирования: δ = I n I n p 1, где p порядок точности используемой формулы. Если δ ε, то мы опять удваиваем текущее значение n и повторяем описанный процесс. Данный алгоритм не учитывает локальный характер поведения подынтегральной функции fx). Общее количество узлов равномерной сетки подбирается с учетом наихудшего поведения fx) на отдельных участках которые могут иметь небольшую суммарную длину), при этом не учитываются участки, где fx) меняется медленно. Такие алгоритмы называют неадаптивными. 3
31 Рассмотренный алгоритм удобен при применении формул Ньютона Котеса, для которых нетрудно реализовать составные формулы. Для формул Гаусса этот алгоритм неудобен, т.к. надо хранить в программе большое число узлов и коэффициентов изза того, что заранее неясно, какое n окажется пригодным Модификация простейшего алгоритма Отрезок [, b] разбивается на n подотрезков частей), а затем на каждом подотрезке применяется выбранная квадратурная формула. В процессе вычислений приближенные значения интегралов по подотрезкам суммируются, что дает в результате приближение I n по всему отрезку. Затем n удваивается, вычисляется I n, после чего поступают как в алгоритме Данная модификация обладает теми же недостатками, но более удобна для применения формул Гаусса, т.к. требует хранения узлов и коэффициентов только одной выбранной формулы. Контроль точности разумно вести по критерию: δ 32 формулой с n узлами. Однако формула с n + 1 узлами ненамного точнее формулы с n узлами, поэтому вычисление оценки погрешности примерно столь же трудоемко, как и вычисление самого интеграла. Поэтому более эффективен другой подход. Возьмем формулу Гаусса с n узлами и построим другую формулу она называется формулой Гаусса Кронрода) с теми же n узлами и с n + 1 дополнительными узлами: b fx)dx = n c i fx i ) + n d j fξ j ) + R n+1 f). Узлы ξ j и коэффициенты c i, d j подбираются так, чтобы данная формула имела полиномиальный порядок точности 3n + 1. Выполним оба просчета по формуле Гаусса с n узлами и по новой формуле с n+1 узлами, затратив на это n+1 вычислений значений подынтегральной функции. Разность между этими просчетами принимается за оценку погрешности. Таким образом при просчетах по формулам Гаусса с n и n+1 узлами и по формуле Гаусса Кронрода с n и n+1 узлами требуется одинаковое количество вычислений fx) в n + 1 точках, однако результат, полученный по формуле Гаусса Кронрода, гораздо более точен. Пользуясь свойствами формул Гаусса Кронрода, алгоритм можно представить следующим образом. Возьмем формулу Гаусса с тремя узлами, добавим четыре узла по Кронроду, а затем выполним вычисления по обеим формулам. Если их разность, являющаяся оценкой погрешности, больше предписанной точности, то добавляем еще 8 узлов всего получается 15), вычисляем приближенное значение интеграла по новой формуле Гаусса Кронрода и сравниваем полученный результат с результатом по предыдущей формуле. Если точность не достигнута, то добавляем еще 16 узлов всего получается 31 узел) и т.д. Данное видоизменение алгоритма обеспечивает механизм получения все более точных результатов без потери ранее вычисленных значений подынтегральных функций. Если заданная точность так и не оказалась достигнутой, то исходный отрезок [, b] можно разбить на два подотрезка и на каждом из них применить описанный алгоритм. 34 j=1
33 Адаптивный алгоритм последовательного передвижения слева направо Рассмотрим адаптивный алгоритм т.е. алгоритм, учитывающий при контроле точности локальное поведение подынтегральной функции), который широко применяется при интегрировании обыкновенных дифференциальных уравнений. Зададимся некоторым шагом h b и вычислим приближенное значение I h интеграла I по выбранной элементарной квадратурной формуле на отрезке [, + h]. Затем вычислим по той же формуле два приближения на отрезках [, + h/] и [ + h/, + h] и сложим их. Полученную сумму обозначим I h/. Вычислим локальную погрешность на шаге h по первой формуле Рунге: δ h = I h/ I h p 1. Если δ h > mxε A, ε O I h/ ), то положим h = h/ и повторим вычисления. В противном случае считаем, что локальная погрешность обеспечивает заданную точность и текущий шаг, который обозначим через h 1, признается удачным. Теперь возникает вопрос: каким должен быть следующий шаг? Здесь возможны два случая: либо следующий шаг выбирается равным предыдущему, либо, если текущая локальная погрешность очень мала например, мы находимся в области гладкости подынтегральной функции), то следующий шаг следует выбрать б ольшим, чем предыдущий. Часто выбирают следующую стратегию. Если δ h > 1 p mx ε A, ε O I h/ ), то следующий шаг h полагается равным h 1, в противном случае берем h = h 1. Такое удвоение обосновывается возможным прогнозом о гладкости подынтегральной функции на следующем шаге. Показатель p выбирается из таких соображений. Для следующего шага h имеет место соотношение h ) p, I I h/ c 35
34 причем на предыдущем шаге h 1 было выполнено c h1 ) p 35 глобальная ошибка не превосходила заданной точности ε ведь обычно задают желаемую величину малости не для локальной, а именно для глобальной ошибки). Таким критерием является δ i h i ε. 15) b Действительно, обозначив через n общее число шагов, а через I i точное значение интеграла на i-м отрезке, имеем: E = I I = n ) n Ihi/ I i I hi/ I i n I hi/ I hi n p 1 = n h i δ i b ε = ε. Итак, более строгий критерий ориентирован на худший случай. Однако естественно ожидать, что в сумме E = n δ i будут встречаться δ i разных знаков, которые будут взаимно уничтожаться, хотя и не полностью. Поэтому при использовании критерия 15) значение E может оказаться излишне меньшим ε, т.е. результат будет получен с завышенной точностью. Вследствие этого часто использую более слабый критерий, задавая для локальной ошибки значение ε примерно равным ε/b ), где ε требуемая точность для всего отрезка интегрирования. При этом достигается экономия вычислительной работы. Для формул Ньютона Котеса замкнутого типа на равномерной сетке дополнительная экономия достигается также, если запоминать значения подынтегральной функции в общих, уже использованных узлах. Например, если в качестве расчетной формулы была выбрана формула Симпсона, то на шаге h i она она использует три узла, а на двух шагах h i / пять узлов, причем три из них уже использованы. Следовательно, во втором применении формулы Симпсона требуется лишь два новых значения fx). Ясно, что при передвижении вправо с шагом h i+1 должны использоваться значения fx), уже вычисленные в правом конце i-го подотрезка. Кроме того, при каждом делении h i пополам следует запоминать узлы и значения fx) из правой половины для последу- 37
36 ющего использования. Поскольку надо заранее учитывать максимальный объем памяти ЭВМ для хранения этих величин, то задается предел HALFMAX на уровень деления отрезка пополам. Когда этот максимум достигнут, то текущий подотрезок считается в любом случае приемлемым, даже если локальная ошибка на нем слишком велика. Длина такого подотрезка может быть сделана совсем небольшой, если выбрать HALFMAX достаточно большим: например, если HALFMAX=3, то длина подотрезка равна b )/ 3. Отметим возникающее при этом важное обстоятельство. Появление такого рода подотрезка заданной минимальной длины означает, что fx) имеет внутри него некоторую особенность например, неинтегрируемую особенность). Поэтому необходимо сообщить пользователю границы подотрезка для последующего осмысления результата. Поскольку длина такого подотрезка мала, то можно надеяться, что локальная ошибка на нем все же не очень большая и при дальнейшем интегрировании она может быть компенсирована другими локальными ошибками, имеющими противоположные знаки. Поэтому процесс разумно продолжить, а не прерывать расчеты. При таком подходе мы имеем возможность не только получить в конечном счете значение интеграла с глобальной ошибкой, меньшей предписанного ε, но и выявить все точки особенностей fx), препятствующие получению локальных погрешностей с приемлемой точностью. Такой подход к составлению программы численного интегрирования позволяет всегда получить приближенное значение интеграла; при этом, если предписанная точность не достигнута, то выдается наилучший возможный для нее результат, оценка E реально достигнутой точности и, если это имеет место, точки особенностей неинтегрируемости) fx). Если в случае формул Ньютона Котеса замкнутого типа удается достигнуть максимальной экономии вычислений fx), то для формул Гаусса этого сделать нельзя, поскольку узлы при их применении на всем подотрезке и на двух его половинах будут совершенно различными. Поэтому применение правила Рунге для оценки локальной погрешности для формул Гаусса будет неэффективно с точки зрения производимых затрат. Для уменьшения трудоемкости применяют формулы Гаусса Крон- 38
http://pandia.ru/text/78/094/7669.php
http://docplayer.com/37558990-I-o-arushanyan-praktikum-na-evm-chislennoe-reshenie-integralnyh-uravneniy-metodom-kvadratur-moskovskiy-gosudarstvennyy-universitet-im-m-v.html