Метод ломаных эйлера дифференциальные уравнения

Метод Эйлера (метод ломаных)

Численные методы решения обыкновенных дифференциальных уравнений

,

связывающее неизвестную функцию y(x), независимую переменную x и производные неизвестной функции, называется обыкновенным дифференциальным уравнением. Порядок n старшей производной называется порядком дифференциального уравнения.

В задаче Коши для дифференциального уравнения n-го порядка искомая функция y(x) кроме самого дифференциального уравнения должна удовлетворять начальным условиям

Методы решения задач для дифференциальных уравнений можно разбить на три типа: точные, приближенные и численные [9].

Точными называют методы, с помощью которых решение дифференциального уравнения можно выразить через известные функции (элементарные функции или интегралы от элементарных функций). Точные методы решения известны только для некоторых классов дифференциальных уравнений (линейные дифференциальные уравнения, уравнения с разделяющимися переменными и др.).

Приближенными называются методы, в которых решение находят как предел последовательности функций, являющихся элементарными или интегралами от элементарных функций. Например, метод разложения искомой функции в ряд Тейлора является приближенным методом.

Численный метод решения дифференциального уравнения — это алгоритм вычисления значений искомого решения y(x) на некотором дискретном множестве значений аргумента x. При этом вычисляемые значения искомого решения y(x) являются приближенными, но могут быть и точными.

Задача Коши

Рассмотрим задачу Коши для обыкновенного дифференциального уравнения первого порядка

(7.1)

. (7.2)

Требуется найти функцию , которая удовлетворяет уравнению (7.1) на интервале (x₀, X) и начальному условию (7.2) в точке x₀.

Приведем без доказательства теорему существования и единственности решения задачи Коши.

Теорема 7.1. Пусть в области функция f(x, y) непрерывна. Тогда на некотором отрезке существует решение уравнения (7.1), удовлетворяющее условию (7.2).

Если в области R функция f(x, y) удовлетворяет условию Липшица

,

то указанное решение единственно.

Произведем разбиение отрезка [x₀, X] на n частей

(7.3)

Найдем приближенные значения решения y(x) в точках x_i, i = 1, 2, …, n.

Метод Эйлера (метод ломаных)

Рассмотрим уравнение (7.1) в точках x_i, i = 0, 1, …, n – 1 и заменим производную 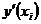разностной формулой

. (7.4)

Тогда получим рекуррентную формулу метода Эйлера для вычисления приближенных значений y(x_{i + 1}):

(7.5)

На рис. 7.1 дана геометрическая иллюстрация метода Эйлера (7.5). Уравнение касательной к графику решения y(x) в точке (x₀, y₀) имеет вид

(7.6)

так как . Интегральная кривая y(x) на отрезке [x₀, x₁] заменяется отрезком касательной (7.6), соединяющей точку (x₀, y₀) с точкой (x₁, y₁), где (см. рис. 7.1). Точка (x₁, y₁) уже не лежит на интегральной кривой y = y(x), удовлетворяющей начальному условию (7.2).

При i = 1 формула (7.5) дает точку (x₂, y₂), которая определяется с помощью касательной проведенной в точке (x₁, y₁) к интегральной кривой y(x), удовлетворяющей уравнению (7.1) и начальному условию .

Таким образом, с каждым шагом i метод Эйлера (7.5) дает точки (x_i, y_i), которые, вообще говоря, удаляются от интегральной кривой, соответствующей точному решению задачи Коши (7.1), (7.2). Вместо интегральной кривой метод Эйлера дает ломаную, изображенную на рис. 7.1, поэтому его часто называют методом ломаных.

Формулу (7.5) можно получить и другим способом. Рассмотрим разложение искомого решения y(x) в ряд Тейлора в окрестности точки x₀:

Ограничившись двумя слагаемыми и учитывая, что , при x = x₁ получим (7.5).

Мы также получили следующий результат — погрешность вычисления значения y₁ есть величина порядка O(h 2 ), а погрешность значения y_n — величина порядка O(h). Из-за большой погрешности метод Эйлера применяется редко.

Пример 7.1. Решить методом Эйлера на отрезке [1, 2] задачу Коши

Решение в программе Excel. Точным решением данной задачи является функция .

Выберем шаг h = 0,1.

В диапазоне A1:B12 заполняем ячейки, как показано в таблице 7.1.

В ячейке D2 записываем начальное значение y(0) = 1, а в ячейке C2 — формулу =(1+C2^2)*0,5/A2, которая соответствует выражению f(x₀, y₀). Затем выделим ячейку C2 и маркером заполнения протянем вниз до C11.

В ячейку D3 введем формулу =D2+0,1*C2 и протянем ячейку D3 маркером заполнения вниз до D12.

В столбце E2:E12 вычислим значения точного решения. Для этого в ячейку E2 введем формулу =TAN(LN(КОРЕНЬ(A2))) и протянем ячейку E2 маркером заполнения вниз до E12.

В столбце F2:F12 вычислим абсолютные ошибки с помощью формулы =ABS(C2-D2), введенной в ячейку F2 и скопированной в остальные ячейки.

Как видим, значения, полученные методом Эйлера, приближенно равны точным значениям. Абсолютная погрешность каждого значения равна в среднем ε ≈ 0,01. При этом видно, что погрешность y_i+1 увеличивается вместе с номером i.

y(x)Ошибки200,0476910,002309420,0914140,004154530,131940,005676640,1698420,006964750,2055560,00808860,2394260,009065970,271720,009951080,3026580,0107581190,3324180,0115031210

0,361150,0122

Создадим в программе Excel пользовательские функции для решения задачи Коши (7.1), (7.2) методом Эйлера, используя встроенный язык Visual Basic. Правую часть уравнения (7.1) для нашего примера определяет функция fxy(x, y):

Function fxy(ByVal x, ByVal y): fxy = (1 + y ^ 2) / (2 * x): End Function

Метод Эйлера реализует функция Eiler(x0, y0, x, n):

Function Eiler(ByVal x0, ByVal y0, ByVal x, ByVal n)

y1 = y0 + h * fxy(x0, y0): x0 = x0 + h: y0 = y1

Next i: Eiler = y1: End Function

Ключевое слово ByVal в списке параметров указывает на то, что каждый параметр будет передаваться по значению.

Здесь исходными данными являются начальные значения x0, y0, значение переменной x и числовой параметр n, который означает число частей, на которые разбивается отрезок [x0, x], т.е. метод Эйлера применяется с шагом h = (x — x0) / n. Результатом является приближенное значение решения в точке x.

Чтобы ввести эти функции в Excel, выполним команду «Сервис – макрос – Редактор Visual Basic» и в открывшемся окне выбираем пункт меню «Insert – Module» и вводим тексты программ-функций (см. рис. 7.2). Теперь эти функции можно использовать в формулах, как и обычные функции программы Excel.

Переходим в Excel, и построим таблицу решения примера 7.1 с помощью созданных функций. В таблице 7.2 приведены результаты вычислений, а в таблице 7.3 показаны формулы. Уменьшение погрешности по сравнению с таблицей 7.1 объясняется тем, что метод Эйлера в таблице 7.2 применяется с шагом h = 0,01.

Отметим, что правая часть уравнения вызывается в описании функции Eiler. Если понадобится решить задачу Коши с другой правой частью, то достаточно переопределить функцию fxy(x, y).

Рис.7.2. Окно редактора Visual Basic

Создадим в программе Mathcad функции для решения задачи Коши методом Эйлера и вычислим решение в точке x = 2 с шагом h = 0,1 (n = 10) и шагом h = 0,01 (n = 100):

Как видим, результаты расчетов в программе Mathcad совпадают со значениями, полученными в Excel.

Метод Эйлера с уточнением

Для повышения точности метода Эйлера применяют следующий прием. Сначала находят приближенное значение решения по методу Эйлера

,

а затем уточняют его по формуле

Этот метод называется методом Эйлера-Коши, и рекуррентные соотношения для его реализации могут быть записаны в виде:

(7.7)

Метод Эйлера-Коши имеет погрешность порядка O(h 2 ). Геометрическая иллюстрация метода Эйлера-Коши дается на рис. 7.2. Очередное приближение метода Эйлера-Коши соответствует точке пересечения диагоналей параллелограмма, построенного на двух звеньях ломаной метода Эйлера.

Метод Эйлера-Коши является одним из частных случаев методов Рунге-Кутта, которые рассмотрены в следующем пункте.

Методы Рунге-Кутта

Рассмотрим наиболее популярный метод решения задачи Коши — метод Рунге-Кутта. Этот метод позволяет строить формулы расчета приближенного решения практически любого порядка точности.

Выведем формулы метода Рунге-Кутта второго порядка точности. Для этого решение представим куском ряда Тейлора, отбрасывая члены с порядком выше второго. Тогда приближенное значение искомой функции в точке x₁ можно записать в виде:

. (7.8)

Вторую производную можно выразить через производную функции f(x, y), однако в методе Рунге-Кутта вместо производной используют разность

,

соответственно подбирая значения параметров 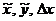. Тогда (7.8) можно переписать в виде

, (7.9)

где α, β, γ и δ — некоторые параметры. Рассматривая правую часть (7.9) как функцию аргумента h, разложим её по степеням h:

,

и выберем параметры α, β, γ и δ так, чтобы это разложение было близко к (7.8). Отсюда следует, что

С помощью этих трех уравнений выразим β, γ и δ через параметр α, тогда получим

(7.10)

Теперь, если вместо (x₀, y₀) в (7.10) подставить (x₁, y₁), то получим формулу для вычисления y₂ — приближенного значения искомой функции в точке x₂.

В общем случае метод Рунге-Кутта применяется на произвольном разбиении отрезка [x₀, X] на n частей, т.е. с переменным шагом

(7.11)

Параметр α выбирают равным 1 или 0,5. Запишем окончательно расчетные формулы метода Рунге-Кутта второго порядка с переменным шагом для α = 1:

(7.12)

(7.13)

Дадим геометрическую интерпретацию методов Рунге-Кутта (7.12), (7.13).

На рисунке 7.3 а) иллюстрируется формула (7.12). Сначала по методу Эйлера вычисляется приближенное значение в точке x_i + h_i/2. В этой точке определяется касательная к интегральной кривой, параллельно которой через точку (x_i, y_i) проводится прямая до точки пересечения с прямой x = x_{i + 1}. Ордината точки пересечения y_{i + 1} принимается за приближенное значение искомого решения в точке x_{i + 1}.

Рисунок 7.3 б) интерпретирует формулу (7.13). Методом Эйлера вычисляется приближенное значение в точке x_i+1. В этой точке тангенс угла наклона касательной к интегральной кривой равен выражению . Через точку (x_i, y_i) проводится прямая, тангенс угла наклона которой определяется как полусумма угловых коэффициентов касательных, проведенных через точки (x_i, y_i) и . За приближенное значение искомого решения в точке x_i+1 принимается ордината точки пересечения этой прямой с прямой x = x_i+1.

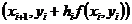
Отметим, что метод (7.13) совпадает с методом Эйлера-Коши (7.7).

Теорема 7.1. Если правая часть f(x, y) уравнения (7.1) непрерывна и ограничена вместе со своими производными до второго порядка включительно, то решение, полученное по формулам (7.12), (7.13), равномерно сходится к решению задачи (7.1), (7.2) с погрешностью .

Приведем наиболее употребительные формулы метода Рунге-Кутта, формулы четвертого порядка точности:

(7.14)

Пример 7.2. Решить методом Рунге-Кутта (7.12) задачу Коши из примера 7.1:

Решение в программе Excel. В таблице 7.4 приведены результаты применения метода Рунге-Кутта второго порядка (7.12) с шагом h = 0,1.

Сравнивая таблицы 7.2 и 7.4 можно увидеть, что метод Рунге-Кутта второго порядка (7.12) с шагом h = 0,1 дает лучшие результаты, чем метод Эйлера с шагом 0,01.

Курсовая работа: Решение дифференциальных уравнений по методу Эйлера

Министерство образования Республики Беларусь

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Кафедра вычислительной математики и программирования

к курсовому проекту

« Решение дифференциальных уравнений по методу Эйлера »

2. Математическое объяснение метода

2.1 Метод Эйлера

2.2 Исправленный метод Эйлера

2.3 Модифицированный метод Эйлера

3. Блок-схема алгоритма программы

4. Описание программы

Список использованной литературы

Приложение 1 (Текст программы)

Приложение 2 (Результаты работы программы)

Уравнение, содержащие производную функции одной переменной, возникают во многих областях прикладной математики. Вообще говоря, любая физическая ситуация, где рассматривается степень изменения одной переменной по отношению к другой переменной, описывается дифференциальным уравнением, а такие ситуации встречаются довольно часто.

Решение обыкновенных дифференциальных уравнений (нелинейных) первого порядка с начальными данными (задача Коши) – классическая область применения численных методов. Имеется много разностных методов, часть из которых возникла в домашинную эпоху и оказалось пригодным для современных ЭВМ.

В этой программе использовался метод Эйлера, один из самых старых и широко известных методов численного интегрирования дифференциальных уравнений. Этот метод имеет довольно большую ошибку; кроме того, он очень часто оказывается неустойчивым – малая начальная ошибка быстро увеличивается с ростом Х. Поэтому чаще используют более точные методы, такие как: исправленный метод Эйлера и модифицированный метод Эйлера. Нужно, однако, заметить, что метод Эйлера является методом Рунге – Кутта первого порядка.

2. Математическое объяснение метода

2.1 Метод Эйлера

Решить дифференциальное уравнение у / =f(x,y) численным методом — это значит для заданной последовательности аргументов х₀ , х₁ …, х_n и числа у₀ , не определяя функцию у=F(x), найти такие значения у₁ , у₂ ,…, у_n , что у_i =F(x_i )(i=1,2,…, n) и F(x₀ )=y₀ .

Таким образом, численные методы позволяют вместо нахождения функции

У=F(x) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=x_k -x_k-1 называется шагом интегрирования.

Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.

Рассмотрим дифференциальное уравнение первого порядка

с начальным условием

Требуется найти решение уравнения (1) на отрезке [а,b].

Разобьем отрезок [a, b] на n равных частей и получим последовательность х₀ , х₁ , х₂ ,…, х_n , где x_i =x₀ +ih (i=0,1,…, n), а h=(b-a)/n-шаг интегрирования.

В методе Эйлера приближенные значения у(х_i )»y_i вычисляются последовательно по формулам у_i +hf(x_i , y_i ) (i=0,1,2…).

При этом искомая интегральная кривая у=у(х), проходящая через точку М₀ (х₀ , у₀ ), заменяется ломаной М₀ М₁ М₂ … с вершинами М_i (x_i , y_i ) (i=0,1,2,…); каждое звено М_i M_i+1 этой ломаной, называемой ломаной Эйлера, имеет направление, совпадающее с направлением той интегральной кривой уравнения (1), которая проходит через точку М_i , смотри рисунок 1.

Если правая часть уравнения (1) в некотором прямоугольнике R<|x-x₀ |£a, |y-y₀ |£b>удовлетворяет условиям:

|df/dx|=|df/dx+f(df/dy)| £ M (M=const),

то имеет место следующая оценка погрешности:

где у(х_n )-значение точного решения уравнения(1) при х=х_n , а у_n — приближенное значение, полученное на n-ом шаге.

Формула (3) имеет в основном теоретическое применение. На практике иногда оказывается более удобным двойной просчет : сначала расчет ведется с шагом h, затем шаг дробят и повторный расчет ведется с шагомh/2. Погрешность более точного значения у_n * оценивается формулой

Метод Эйлера легко распространяется на системы дифференциальных уравнений и на дифференциальные уравнения высших порядков. Последние должны быть предварительно приведены к системе дифференциальных уравнений первого порядка.

2.2 Исправленный метод Эйлера

В исправленном методе Эйлера мы находим средний тангенс наклона касательнй для двух точек: x_m , y_m и x_m +h, y_m +hy’_m . Последняя точка есть та самая, которая в простом методе обозначалась x_m+1 , y_m+1 . Геометрический процесс нахождения точки x_m+1 , y_m+1 можно проследить по рисунку 2. С помощью метода Эйлера находится точка x_m +h, y_m +hy’_m, лежащая на прямой L_1. В этой точке снова вычисляется тангенс угла наклона касательной, на рисунке этому значению соответствует прямая L₂ . Усреднение двух тангенсов дает прямую L’₃ . Наконец, через точку x_m , y_m мы проводим прямую L₃ параллельную L’₃ . Точка, в которой прямая L₃ пересечется с ординатой, восстановленной из x= x_m+1 =x_m +h, и будет искомой точкой y= y_m+1 = y_m +hy’_m . Тангенс угла наклона L₃ равен:

Уравнение линии L₃ при этом записывается в виде:

Соотношения 5, 6, 7 и 8 описывают исправленный метод Эйлера. (рис. 2)

2.3 Модифицированный метод Эйлера

Этот метод более точен. Рассмотрим дифференциальное уравнение (1) с начальным условием y(x₀ )=y₀ . Разобьем наш участок интегрирования на n равных частей. На малом участке [x₀ ,x₀ +h] интегральную кривую заменимпрямой линией. Получаем точкуМ_к (х_к ,у_к ). (рис. 3)

Название: Решение дифференциальных уравнений по методу Эйлера Раздел: Рефераты по математике Тип: курсовая работа Добавлен 20:43:28 26 декабря 2010 Похожие работы Просмотров: 1331 Комментариев: 21 Оценило: 3 человек Средний балл: 5 Оценка: неизвестно Скачать

N_k / _y=y(x)

М_к М_к /

Y_k+1

Y_k

х_к х_к1/2 x_k+h =x_k1 X

Получаем точку N_k / . В этой точке строим следующую касательную:

Из точки М_к проводим прямую с угловым коэффициентом α_к и определяем точку пересечения этой прямой с прямой x_к1 . Получаем точку М_к / . В качестве у_к+1 принимаем ординату точки М_к / . Тогда:

Эти формулы называются рекуррентными формулами метода Эйлера.

Сначала вычисляют вспомогательные значения искомой функции y_к+1/2 в точках x_к+1/2 , затем находят значение правой части уравнения (1) в средней точке

3. Блок-схема алгоритма

где A — начальное значение x, B — конечное значение x, F(x) — значение функции в точке x_n , N — количество промежутков, st – выбор операции, C1,C2,C3 – константы для формул, nom — сохраняет номер используемой функции.

На рисунке представлена блок-схема процесса решения дифференциального уравнения методом Эйлера

Подсчитывая каждый раз новое значение уравнения F(x), получаем последовательность значений x_n y_n , n=1,2,…

По этим значениям строим график.

4. Описание программы

Программа весьма проста. В ней много предусмотрено моментов неправильного ввода данных, о которых программа предупреждает пользователя и сразу же просит повторно ввести данные.

С самого начала программа предоставляет пользователю меню выполняемых функций, которые выделяются при помощи стрелок ↑ и ↓ выбор клавишей Enter:

После запуска программы нужно выбрать Formyla -> Enter, эта опция позволит из предложенного списка формул выбрать одну, по которой компьютер будет производить расчет и строить график. Все предложенные формулы имеют номерацию; чтобы выбрать интересующий вас пример нажмите на цифру равную номеру примера, и сразу же появится новое окно, в котором сверху будет записан ваш пример. Также в окне будет этот же пример но с нулями на месте констант. Под примером будет высвечена большая буква С, это используется для ввода констант. Для этого вам нужно нажать номер константы, он появится, и после знака равно запишите чему она равна (вводятся целые и вещественные значения). По окончании набора нажать Enter. Операцию повторять пока не будут введены все числа. По окончании нажать Esc. После появится строчка «уточните границы изменения Х, от A= до B= » здесь нужно занести данные на каком промежутке абсциссы будет рассматриваться функция. Следующая строчка попросит ввести начальные данные y(A)=. Следующей строчкой будет вопрос: «сохранить данные в файле? Да/Нет» ответить на этот вопрос с помощью клавиш Д и Н (рус), после чего программа вернется в первоначальное меню. Если данные были сохранены (в папке с программой появляется файл form.txt), то в следующий раз чтобы не набирать снова выберите в меню опцию Formyla -> Open in fails и на экране появятся введенные данные с пометкой снизу, сообщая что данные были прочитаны из файла.

Следующая опция Reshenie. После нажатия в окне просят ввести N(целое число) – число промежутков, на которые разделится рассматриваемый участок (ось ОХ). После появится таблица рассчитанных данных (номер точки, значение абсциссы, значение ординаты). При нажатии любой клавиши произойдет переход в меню.

Graphic эта опция позволяет визуально видеть решение, а так же на этом графике прописываются все данные: начальная формула, шаг и промежуток построения графика, масштаб, данные об его изменении(клавишами +(увеличить) и -(уменьшить), а также возможность определить точное значение функции в любой точке.

Опция Exit применяется для выхода из программы.

Результатом выполнения курсового проекта является готовый программный продукт, позволяющий решать дифференциальные уравнения по методу Эйлера, демонстрирующий возможности численного решения поставленной задачи с заданной степенью точности.

Данная программа решает заданную пользователем дифференциальное уравнение за минимальный промежуток времени. При этом пользователю предоставляется возможность визуально оценить решение, рассматривая график полученного решения.

К достоинствам программы можно отнести также удобный пользовательский интерфейс, возможность ввода пользовательских дифференциальных уравнений, а также давольно высокая стабильность работы. Однако имеются и некоторые недостатки. К недостаткам программы можно отнести: критичность к вводимым пользователем урававней, отсутствие обработки исключительных событий. Это, естественно, ограничивает возможности программы.

Список использованной литературы

1. Д. Мак-Кракен, У. Дорн. Численные методы и программирование на фортране. –М.: Мир,1977.-389,396-408 с.

2. А.А. Самарский. Введение в численные методы. – М.:Наука,1987.-176 с.

3. Алгоритмы вычислительной математики: Лабораторный практикум по курсу «Программирование» для студентов 1 — 2-го курсов всех специальностей БГУИР/А.К. Синицын, А.А. Навроцкий.- Мн.: БГУИР, 2002.- 65-69 с.

4. ГОСТ 2.105-95. Общие требования к текстовым документам.

5. ГОСТ 7.32-91. Система стандартов по информации, библиотечному и издательскому делу. Отчет о НИР. Структура и правила оформления.

Приложение 1. Текст программы.

void formyl(int p)

if(p==1) printf(«\n 1. C1*y’ = C2*y + C3*x + C4*x*y»);

else if(p==2) printf(«\n 2. y’/(C1-100) = C2*y + C3*x + (C4+x)*y»);

else if(p==3) printf(«\n 3. pow(e,C1)*y’ = C2*y + C3*cos(x) + (C4+x+y)»);

else if(p==4) printf(«\n 4. C1*sin(x)*y’ = e*C2*y + C3*arcsin(x) + C4*y/x»);

else if(p==5) printf(«\n 5. C1*y’ = sin(C2)*y + tg(C3*x) + C4*ln(x)*y»);

else if(p==6) printf(«\n 6. C1*y’ = y*C2 + C3*sin(x) + C4*cos(x)*y»);

else if(p==7) printf(«\n 7. (C1+C2+C3+C4)*y’ = C2*y + (C3-x) + lg(C4*x)*y»);

else if(p==8) printf(«\n 8. y’/C1 = y/C2 + C3*sin(x) + C4*x*y»);

else if(p==9) printf(«\n 9. sin(C1)*y’ = C2*y + |C3|*x + x*y/C4»);

void formyl2(int p,double C1,double C2,double C3,double C4)

else if(p==2) printf(«y’/(%.2f-100)=%.2f*y+%.2f*x+(%.2f+x)*y»,C1,C2,C3,C4);else if(p==3) printf(«pow(e,%.2f)*y’=%.2f*y+%.2f*cos(x)+(%.2f+x+y)»,C1,C2,C3,C4);

else if(p==4) printf(«%.2f*sin(x)*y’=e*%.2f*y+%.2f*arcsin(x)+%.2f*y/x»,C1,C2,C3,C4);

else if(p==5) printf(«%.2f*y’=sin(%.2f)*y+tg(%.2f*x)+%.2f*ln(x)*y»,C1,C2,C3,C4);

else if(p==6) printf(«%.2f*y’=y*%.2f+%.2f*sin(x)+%.2f*cos(x)*y»,C1,C2,C3,C4);

else if(p==8) printf(«y’/%.2f=y/%.2f+%.2f*sin(x)+%.2f*x*y»,C1,C2,C3,C4);

else if(p==9) printf(«sin(%.2f)*y’=%.2f*y+|%.2f|*x+x*y/%.2f»,C1,C2,C3,C4);

double formyl3(int p,double h,double x,double y,double C1,double C2,double C3,double C4)

else if(p==2) Y=h*(C1-100)*(y*C2+C3*x+(C4+x)*y)+y;

else if(p==3) Y=h*(C2*y+C3*cos(x)+C4+x+y)/exp(C1)+y;

else if(p==4) Y=h*(exp(1)*C2*y+C3*asin(x)+C4*y/x)/(C1*sin(x))+y;

else if(p==5) Y=h*(sin(C2)*y+tan(C3*x)+C4*log10(x)*y)/C1+y;

else if(p==6) Y=h*(y*C2+C3*sin(x)+C4*cos(x)*y)/C1+y;

else if(p==7) Y=h*(C2*y+(C3-x)+log10(C4*x)*y)/(C1+C2+C3+C4)+y;

else if(p==8) Y=h*(y/C2+C3*sin(x)+C4*x*y)*C1+y;

else if(p==9) Y=h*(C2*y+abs(C3)*x+x*y/C4)/sin(C1)+y;

int vv=0,vv1=0; // руководит операциями

int N=0,W; // кол промежутков

int i,j,k; // используются во всех «for»

int nom; // номер примера

int st=4,vst=0; // строчка в меню

double C1,C2,C3,C4; // константы

double M; // масштаб

double xtoch,ytoch; // считает y(x) по графику

double A=0,B=0,ii,jj,kk; // пределы интегрирования

double x[102],y[102]; // главные переменные x,y

int g_driver=9,g_mode=2, g_error;

printf(«\n error=%d, reason=%s\n», g_error, grapherrormsg(g_error));

Метод ломаных эйлера дифференциальные уравнения

Variant 19 (Sukach Maxim, BS17-03)

Найдем

В итоге, наше решение принимает вид:

Метод Эйлера дает возможность приближенно выразить функцию теоретически с любой наперед заданной точностью. Суть метода Эйлера в пошаговом вычислении значений решения y=y(x) дифференциального уравнения вида y’=f(x,y) с начальным условием (x0;y0). Метод Эйлера является методом 1-го порядка точности и называется методом ломаных.

Для вычисления используются следующие формулы:

Метод Эйлера и точное решение при x0 = 0, xf = 9, y0 = 1, h = 0.1

Метод Эйлера и точное решение при x0 = 0, xf = 3, y0 = 1, h = 0.1

Метод Эйлера и точное решение при x0 = 0, xf = 1, y0 = 1, h = 0.1

Усовершенствованный метод Эйлера

Суть усовершенствованного метода Эйлера в пошаговом вычислении значений решения y=y(x) дифференциального уравнения вида y’=f(x,y) с начальным условием (x0;y0). Усовершенствованный метод Эйлера является методом 2-го порядка точности и называется модифицированным методом Эйлера.

Разница между данным методом и методом Эйлера минимальна и заключается в использовании следующих формул:

Усовершенствованный Метод Эйлера и точное решение при
x0 = 0, xf = 9, y0 = 1, h = 0.1

Усовершенствованный Метод Эйлера и точное решение при
x0 = 0, xf = 3, y0 = 1, h = 0.1

Усовершенствованный Метод Эйлера и точное решение при
x0 = 0, xf = 1, y0 = 1, h = 0.1

Классический метод Рунге-Кутты

Суть метода Рунге-Кутты в пошаговом вычислении значений решения y=y(x) дифференциального уравнения вида y’=f(x,y) с начальным условием (x0;y0). Классический метод Рунге-Кутты является методом 4-го порядка точности и называется методом Рунге-Кутты 4-го порядка точности.

Ну и как обычно, формулы:

Классический метод Рунге-Кутты и точное решение при x0 = 0, xf = 9, y0 = 1, h = 0.1

Классический метод Рунге-Кутты и точное решение при x0 = 0, xf = 3, y0 = 1, h = 0.1

Классический метод Рунге-Кутты и точное решение при x0 = 0, xf = 1, y0 = 1, h = 0.1

Сравнение методов для заданной задачи

Размер ошибки всех методов на промежутке [0, 9] с шагом 0.1

Размер ошибки всех методов на промежутке [0, 3] с шагом 0.1

Размер ошибки всех методов на промежутке [0, 1] с шагом 0.1

Очевидно что, классический метод Рунге-Кутты справляется с задачей аппроксимации в случае данного уравнения намного лучше чем Метод Эйлера и Усовершенствованный метод Эйлера.

График глобальной средней ошибки

Глобальная ошибка в зависимости от размера шага H на промежутке от 0.01 до 0.91 для x0 = 1, xf = 9