Метод матричной прогонки для уравнения лапласа

Метод матричной прогонки для решения сеточных уравнений гидродинамики Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Давыденко Б. В.

Предложен прямой метод решения системы конечно-разностных уравнений динамики вязкой жидкости, основанный на матричной прогонке. Метод основан на замене системы алгебраических системой векторных уравнений и применим для решения двумерных задач гидродинамики. В отличие от наиболее распространенных итерационных методов он не требует составления специального уравнения для расчета давления, а позволяет определять его непосредственно из уравнения неразрывности, что обеспечивает высокую точность и надежность получаемых решений

Похожие темы научных работ по математике , автор научной работы — Давыденко Б. В.

Текст научной работы на тему «Метод матричной прогонки для решения сеточных уравнений гидродинамики»

Произведение механических КПД Пт1 и Пт2 дает общий объемный КПД ГОП как в прямом, так и в обратном потоках мощности с учетом соответствующих соотношений для этих КПД.

Уточнена лемма [7] о наличии или отсутствии циркуляции мощности в бесступенчатых двухпоточ-ных ГОМТ. На основании леммы режимы прямого или обратного потоков мощности через гидрообъемную передачу, работающую в составе двухпоточных ГОМТ, связаны с регулировочной характеристикой трансмиссии. 2. Получены универсальные соотношения для объемного и механического КПД объемных гидромашин аксиально-поршневого типа (на примере модели Городецкого К.И.), входящих в состав двухпо-точных ГОМТ и работающих в режимах циркуляции мощности.

1. Аврамов В.П., Самородов В.Б. Гидрообъемные передачи в гидрообъемных трансмиссиях транспортных машин: Учеб. Пособие.-Харьков:ХПИ.-1986.-76с.

2. Епифанов В.В., Самородов В.Б. Кинематические и силовые характеристики гидрообъемно-механической транс-

миссии с учетом к.п.д. при прямолинейном движении транспортной машины // Теория механизмов и машин.-Харьков: Вища школа.- 1982.- Вып.32.- С.65-70.

3. Городецкий К.И.. Механический КПД объемных гидромашин //Вестник машиностроения.- 1977.- №7.- С.19-23.

4. Городецкий К.И., Михайлин А.А. Математическая модель объемных гидромашин //Вестник машиностроения.- 1981.- №9.- С.14-17.

5. Колесные и гусеничные машины высокой проходимости (конструкции, теория, проектирование, расчет, производство, эксплуатация) в10-ти томах. Том 3: Трансмиссии, Книга 2: Бесступенчатые трансмиссии: расчет и основы конструирования / В.Б. Самородов, Е.Е. Александров, Д.О. Волонцевич, А.С. Палащенко / под ред. Е.Е. Александрова. — Харьков.: ХГПУ, 1997.-185 с.

6. Объемные гидравлические привода / Т.М. Башта, И.З. Зайченко, В.А. Ермаков и др. — М.: Машиностроение, 1969.- 627 с.

7. Самородов В.Б., Волонцевич Д.О., Рогов А.В. Уточненная методика определения потерь в планетарных механизмах передачи и результаты исследования потоков мощностей в гидрообъемно-механических трансмиссиях. // 1нтегроваш технологи та енергозбереження. — Харюв: ХДПУ. — №4, 2001. — С. 105 — 109.

Предложен прямой метод решения системы конечно-разностных уравнений динамики вязкой жидкости, основанный на матричной прогонке. Метод основан на замене системы алгебраических системой векторных уравнений и применим для решения двумерных задач гидродинамики. В отличие от наиболее распространенных итерационных методов он не требует составления специального уравнения для расчета давления, а позволяет определять его непосредственно из уравнения неразрывности, что обеспечивает высокую точность и надежность получаемых решений

МЕТОД МАТРИЧНОЙ ПРОГОНКИ ДЛЯ РЕШЕНИЯ СЕТОЧНЫХ УРАВНЕНИЙ ГИДРОДИНАМИКИ

Кандидат технических наук, ведущий научный сотрудник Институт технической теплофизики НАН Украины ул. Желябова, 2а, г. Киев, Украина, 03057. Контактный телефон: (044) 424-96-44, E-mail: bdavydenko@ukr.net

Для решения задач динамики вязкой жидкости обычно используются конечно-разностные методы 1, предполагающие замену дифференциальных уравнений переноса импульса и неразрывности дис-

кретными уравнениями, составленные на разностной сетке относительно сеточных функций скорости и давления. Система дифференциальных уравнений, таким образом, заменяется системой разностных алгебраических уравнений, которая решается тем или иным способом. Наибольшее распространение полу-

чили способы решения разностных уравнений, основанные на методе итераций для расчета поля давления и удовлетворения уравнению неразрывности. Из них следует выделить алгоритм SIMPLER [4], лежащий в основе большинства современных пакетов прикладных программ для решения задач гидродинамики. Характерной особенностью итерационных методов является необходимость построения на основе уравнения неразрывности специального уравнения для расчета давления, которое, в отличие от уравнений количества движения, является для несжимаемых жидкостей стационарным.

При необходимости исследования решения нестационарных течений необходимо на каждом шаге по времени получать сходящееся решение уравнения для давления, иначе найденное на данном шаге по времени поле скоростей не будет удовлетворять уравнению неразрывности.

Такой подход к решению задач динамики с удовлетворительной точностью требует значительных затрат времени для вычислений. В отличие от традиционных алгоритмов, прямой неявный метод, предлагаемый в данной работе, позволяет решать все три уравнения динамики одновременно. Для этого система разностных алгебраических уравнений преобразовывается в систему векторных уравнений, решаемых методом прогонки вдоль одной из выбранных координат

Метод матричной прогонки обычно используется для численного решения двумерного уравнения теплопроводности [5].

Для исследования течений вязкой жидкости он применялся в [6], однако в этом случае уравнения динамики записывались в переменных «функция тока — вихрь».

В данной работе предлагается вариант метода матричной прогонки для случая записи исходных уравнений в физических переменных «проекции вектора скорости — давление»

2. Переход от системы разностных уравнений к системе векторных уравнений

Рассмотрим систему уравнений динамики вязкой жидкости для двумерных течений

Эи dv „ —+ — = 0 Эх ду

dv dv dv — + и— + v— дт dx dy

n d2V J +2v—S— dy2 dx

P dy dv + du dx dy

где х; у — прямоугольные координаты; т — время; и, V — составляющие вектора скорости; р — давление; р — плотность; V — кинематический коэффициент вязкости.

Элемент прямоугольной «разнесенной» разностной сетки, на котором выполняется дискретизация пространственных производных системы уравнений (1) — (3) изображен на рис. 1

Рис. 1. Разнесенная разностная сетка для дискретизации уравнений динамики

Конечно-разностная аппроксимация системы (1) — (3), выполненная по неявной временной схеме, будет после линеаризации иметь вид:

+ U* i,j [cux (u j -U i, j ) + (l-Cux )(u i,j-U j )] / dx +

+V* i 1/2, j+1/2 [CUy (U i+1, j- U i, j)+(1-CUy )(U i, j- U i-1, j)] /d У =

= (Pij-Pij+1)/(PdX) + +2V(Ui, j+1-2 Ui, j+ Ui, j-1) / dX2 +

+V(Ui+1,j-2 Ui, j + Ui, j-1)/ d y2 + +V(V u+1-V i,j-V i-1,j+1+V i-1, j)/ d y/ d x;

(V. V* ., / Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Затем соотношения (13)-(16) подставляются в уравнение (11). Это уравнение преобразовывается уже с учетом полученного выражения (17). Из преобразованного уравнения (11) уравнения исключается вектор и1

и = S1U и +1+ S2U У1 +1 + S4U Р’1 + S5U Р1 +1+Ф и (18)

где SlU=-nU(AU+SзUS2У); S2U=-nUSзUSlУ; S4U=-nU(DU +SзUS4У)

Подстановка полученного выражения (18) в соотношение (17) приводит к равенству

где GlV= S1V+SзVS2U; G2V=S2V+SзVS1U; G4V=S4V+SзVS4U; G5V = S5V+SзVS5U;

Следующий этап решения задачи состоит в исключении из выражений (18) и (19) векторов Р’ и Р1+1. Как это следует из представления (15), вектор Р’ будет присутствовать в выражениях (18) и (19) лишь в том случае, если хотя бы одна из сеточных переменных 71-11] будет равна единице. Другими словами, вектор Р ‘1 будет иметь компоненты, отличные от нуля, если горизонталь сетки с номером 1-1 пересекает участок расчетной области, занятый твердотельными включениями, а следующие за ними ячейки с номерами 1 будут принадлежать области течения. Для исключения Р’ необходимо воспользоваться уравнением неразрывности (7).

Ввиду того, что составляющие вектора Р’1 по определению равны нулю при 71^ = 0, уравнение (7) будет рассматриваться не для всех ] (1 1.

Прямая матричная прогонка заканчивается после расчета матриц Xi, Yi и векторов Zi для последнего шага 1=М. Вследствие особенностей используемой разнесенной сетки к выражениям (13)-(16), составленным для 1=М, добавляется еще одно соотношение

UM = X UM ■ UM+1+ Y UM ■ V M +ZUM

Следующий этап состоит в вычислении векторов и1, У1, Р1 для всех значений 1. Для этой цели используются указанные рекуррентные соотношения и граничные условия при у=утах. Из граничных условий при у=утах обычно бывают известными векторы УМ, им+1, или векторы Рм, им+1.

Далее, последовательно для всех шагов 1 от 1=М-1 до 1=1 с помощью соотношений (13) — (16) рассчитываются векторы и1 , У1 и Р1. Таким образом определяются поля скоростей и давления для текущего момента

времени. Для следующего шага по времени после корректировки коэффициентов разностных уравнений вычислительная процедура повторяется.

Рассмотренный прямой метод решения системы разностных уравнений динамики вязкой жидкости имеет ряд преимуществ по сравнению с широко распространенными итерационными методами. Он позволяет использовать неявную схему аппроксимации, что обеспечивает его абсолютную устойчивость по отношению к величине шага по времени. Кроме того, данный метод обеспечивает любую заранее выбранную точность решения разносных уравнений, а также надежность получаемых результатов. К недостаткам метода следует отнести большее по сравнению с традиционными методами количество арифметических операций. Вследствие этого увеличиваются требования к быстродействию и объему оперативной памяти вычислительных средств. Однако для современных персональных компьютеров данное требование уже не является лимитирующим.

1. Андерсон Д., Таннехилл Дж, Плетчер Р. Вычислительная гидромеханика и теплообмен. — М. : «Мир», 1990.- т.1.-384 с.

2. Пейре Р., Тейлор Т. Д. Вычислительные методы в задачах механики жидкости. — Л.: Гидрометеоиздат, 1986.- 352 с.

3. Роуч П. Вычислительная гидродинамика. -М.: Мир, 1980. -616с.

4. Патанкар С. Численные методы решения задач теплообмена и динамики жидкости. — М.: Энергоатомиздат, 1984. — 152 с.

5. Самарский А.А., Николаев Е.С. Методы решения сеточных уравнений. — М.: Наука, 1978.- 549 с.

6. Калис Х.Э., Цинобер А.Б. Плоскопараллельное течение вязкой несжимаемой жидкости в каналах под влиянием поперечного магнитного поля // Изв. СО АН СССР. Сер. технических наук.- 1967.-вып. 2, № 8.- С. 16 — 22.

9.4.1. Метод матричной прогонки

Запишем разностную схему (9.14) в виде:

Положим в формулах (9.15) N=1,2,…,N-1 и, используя (9.16), запишем систему уравнений (9.15) в векторной форме :

Um+1+AUm+Um-1=fm , m = 1,2,…, M-1 (9.17)

Где A – трехдиагональная матрица порядка M-1 C диагональным преобладанием, т. к. |1+a|>|a|, a>0 .

A=,

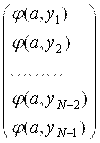
Fm = , J0 = , JA = .

Задача (9.17) аналогична задаче в п.9.3.3, отличие состоит лишь в том, что она имеет векторную форму. Предполагаем, что между соседними значениями векторов этого решения Um существует связь

Где Rk – это матрицы, Sk – векторы.

При K=0 R0=0 U0=J0, S0=J0 — Задано. Возьмем K=M-1 , запишем (9.18) , подставим в (9.17), затем опять преобразуем к виду (9.18). Получим соотношения для вычисления матриц и векторов

Вычислим матрицы Rk = — ( A + Rk-1)-1 и векторы Sk= Rk (Sk-1—Fk), Для K=1. M-1. Что позволит, используя данное значение вектора на границе UM=JA , вычислить последовательно искомые значения вектора решения по формуле