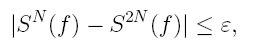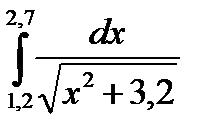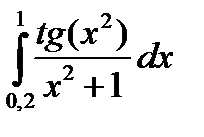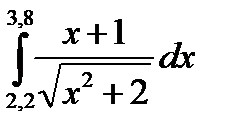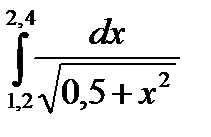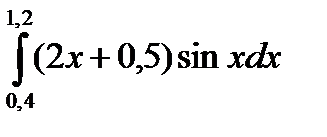Решение дифференциальных уравнений методами Эйлера и Милна
Автор работы: Пользователь скрыл имя, 02 Мая 2014 в 20:48, курсовая работа
Краткое описание
Дифференциальные уравнения чаще всего применяются для описания динамических (т.е. изменяющихся во времени) математических моделей и реально протекающих процессов, что, несомненно, характеризует их решение как исключительно важный и актуальный аспект в науке и производстве. Целью данной курсовой работы является углубленное рассмотрение возможностей численного решения дифференциальных уравнений. В задачи работы входит изучение методов Эйлера и Милна и рассмотрение примеров решений данными методами обычного дифференциального уравнения первого порядка.
Содержание
Введение 5
1. Задача Коши для обыкновенного дифференциального уравнения первого порядка 7
1.1. Постановка задачи Коши. 7
1.2. Разрешимость задачи Коши. 8
2. Классификация приближенных методов решения ОДУ с начальными условиями 10
3. Метод Эйлера – разные подходы к построению 13
3.1. Геометрический способ. 13
3.2. Применение формулы Тейлора. 15
3.3. Разностный способ. 16
3.4. Квадратурный способ 17
4. Несколько простых модификаций метода Эйлера 19
4.1. Неявный (обратный) метод Эйлера 19
4.2. Неявный метод Эйлера-Коши (метод трапеций) 19
4.3. Метод Эйлера-Коши (метод Хойна) 20
4.4. Метод Эйлера-Коши с итерационной обработкой 20
4.5. Уточненный метод Эйлера 21
Пример 1. 22
5. Исправленный метод Эйлера 28
6. Пошаговый контроль точности 30
Пример 2. 31
7. Методы прогноза и коррекции. Метод Милна 35
Пример 3. 40
8. Системы дифференциальных уравнений первого порядка Дифференциальные уравнения высших порядков 46
Заключение 48
Список используемой литературы 49
Приложение А 50
Вложенные файлы: 1 файл
Курсовая.docx
Дифференцируя (2.1), по формуле полной производной
находим приближенное значение второй производной:
Подставляя приближенные выражения , и в равенство (5.2), получаем следующую формулу для вычисления при
Определяемый ею метод называется исправленным методом Эйлера.
Так как при формулы (5.3) и (5.4) точны, а , согласно начальному условию (2.2), то на первом шаге вычислений по формуле (5.5) будет совершаться ошибка, связанная только с усечением ряда Тейлора. Следовательно, локальная ошибка или, иначе, шаговая погрешность метода (5.5) составляет величину , а это означает, что исправленный метод Эйлера относится к методам второго порядка [2].
- Пошаговый контроль точности
Нетрудно понять, что выведение надежных и, в то же время, простых и эффективных оценок погрешности, гарантирующих получение таблицы значений решения заданной точности, является делом малоперспективным, особенно для методов более-менее высоких порядков. Поэтому главным способом отслеживания точности при реализации численных процессов решения задачи Коши остается применение различных полуэмпирических правил, основанных на принципе Рунге.
Будем считать, что при использовании метода p-го порядка абсолютная шаговая погрешность должна находиться в пределах . Тогда, согласно принципу Рунге, осуществляется счет по системе узлов с шагом и по системе узлов с шагом . При четных вторая система будет совпадать с первой, т.е. . Переход от расчетной точки с приближенным значением решения в ней к расчетной точке один раз совершается за один шаг длины и приводит к значению
, другой раз совершается за два шага длины («транзитом» через точку со значением
) и дает значение
Поправка Ричардсона в таком случае будет составлять величину
Если величина меньше заданного , то можно считать, что ошибка приближенного равенства не превосходит . Если же , то следует уменьшить расчетный шаг .
При условии стоит попытаться двигаться дальше с более крупным шагом (например, удвоить ).
Пример 2. (продолжение примера 1., см. главу 4)
Посмотрим, что дает применение принципа Рунге к нескольким простым методам численного решения того же уравнения с начальным условием . Из точки перейдем в точку за один шаг используя явный и неявный методы Эйлера, метод трапеций и метод Хойна. С помощью полученных значений и найденных ранее теми же методами в примере 1 значений
подсчитаем поправки Ричардсона
при для явного и неявного методов Эйлера и для методов трапеций и Хойна. Найдем уточненные приближенные значения решения путем прибавления к значениям поправок Ричардсона . Найдем их истинные погрешности
Метод Эйлера (3.3)
Начинаем процесс вычислений
Достигли нужной точки, процесс вычислений закончен.
Неявный метод Эйлера (4.1)
Начинаем процесс вычислений
Достигли нужной точки, процесс вычислений закончен.
Метод трапеций (4.2)
Начинаем процесс вычислений
Достигли нужной точки, процесс вычислений закончен.
Начинаем процесс вычислений
Достигли нужной точки, процесс вычислений закончен.
Занесем результаты вычислений в таблицу:
В эту таблицу последним столбцом помещен последний столбец из таблицы результатов примера 1., содержащий погрешности значений . Сравнение с ним столбца со значениями поправок Ричардсона показывает, что эти поправки хорошо отражают поведение погрешностей методов (хотя и не дают основание считать их модули оценками погрешностей), а предпоследнего – эффективность уточнения по правилу Рунге-Ричардсона.
- Методы прогноза и коррекции. Метод Милна
Не смотря на то, что метод Эйлера достаточно прост, из-за недостатка точности он редко используется на практике для получения конечного ответа . Задачи, которые ставятся сегодня перед инженерами, математиками и физиками требуют гораздо более точных методов расчета приближенных решений дифференциальных уравнений.
Для случаев, когда требуется достичь вполне определенной точности , применяют так называемые методы прогноза и коррекции (схемы предиктор-корректор, методы предсказания и уточнения), заключающиеся в совместном применении явных и неявных методов одинакового или смежных порядков. По явной формуле значение решения задачи (2.1) – (2.2) в текущей (расчетной) точке прогнозируется, т.е. находится его, быть может, достаточно грубое приближение, а с помощью неявной формулы, в правую часть которой подставляется спрогнозированное значение, оно уточняется (корректируется) [2]. Примерами методов прогноза и коррекции могут служить ранее рассмотренные метод Хойна, метод Эйлера-Коши с итерационной обработкой, уточненный метод Эйлера.
Далее рассмотрим еще один широко известный метод прогноза и коррекции – метод Милна. Сначала дадим описание этого метода, затем рассмотрим вывод необходимых формул, применяемых в методе.
Пусть дано дифференциальное уравнение (2.1) с начальным условием (2.2). Выбрав шаг положим, как обычно, , ,
Обозначим для краткости
Первые четыре значения искомого решения (т.н. «начальный отрезок») находим, используя начальное условие (2.2) и применяя какой-либо численный метод решения ОДУ (например, метод Эйлера). Тем самым будут известны , .
Дальнейшие значения последовательно определяются по следующей схеме: предполагая, что известны,
- вычисляем первое приближение для ближайшего следующего значения по формуле
- значение подставляем в дифференциальное уравнение (2.1) и определяем соответствующее значение
- находим второе приближение по формуле
Милн показал, что абсолютная погрешность значения приближенно равна
Поэтому если , где — заданная предельная погрешность решения, то можно положить и . В частности, это имеет место, если совпадают в интересующих нас десятичных знаках.
Далее переходим к вычислению ближайшего следующего значения , повторяя указанный выше процесс. В противном случае, если точность не достигнута, следует уменьшить шаг . При этом необходимо осуществить пересчет соответствующего «начального отрезка».
Метод Милна выгодно отличается от других методов тем, что в нем производится корректировка каждого вновь полученного частного значения интеграла уравнения без пересчета с измененным шагом.
Далее приступим к выводу формул метода Милна (7.1) – (7.3). Для этого запишем общий вид первой интерполяционной формулы Ньютона:
где , , а выражения вида – конечные разности
Воспользуемся данной формулой, написанной для производной , в подходяще выбранной точке , причем ограничимся разностями третьего порядка, что равносильно тому, что интеграл дифференциального уравнения (2.1) аппроксимируется полиномом четвертой степени. Имеем
Полагая в формуле (7.4) и почленно интегрируя полученную формулу по в пределах от до , будем иметь
Отсюда, учитывая, что и , находим
то, подставляя эти значения в формулу (7.6), после обычных упрощений получим первую формулу Милна:
Для вывода второй формулы Милна положим в формуле (7.4) и проинтегрируем обе части получившегося выражения по в пределах от до , будем иметь
Отсюда, выполняя квадратуры, получим
Подставляя в формулу (7.8) известные выражения
придем ко второй формуле Милна:
Для вывода контрольной формулы (7.3) для погрешности второго приближения оценим главные члены погрешностей и первой и второй формул Милна. Учитывая отброшенные в интерполяционной формуле Ньютона (7.4) разности четвертого порядка, с точностью до разностей пятого порядка будем иметь
Отсюда, считая, что четвертая разность постоянна на интервале длины , получим .
Так как, очевидно, и , то
Следовательно, имеем контрольную формулу Милна:
Заметим, что если шаг достаточно мал, то приближенно можно положить
Пусть – интересующий нас отрезок, на котором строится решение дифференциального уравнения (2.1), и Тогда из формул (7.10) следует, что предельная абсолютная погрешность на отрезке приближенного решения выражается следующим образом:
Таким образом, глобальная ошибка метода Милна есть величина порядка [4].
Пример 3. (продолжение примера 1., см. главу 4)
Дано уравнение с начальным условием . Найдем методом Милна приближенное значение решения в точке с точностью до
Метод Милна имеет глобальную ошибку , это значит, что взяв , получим погрешность результата порядка , таким образом, заданная точность практически достигается.
Решение дифференциальных уравнений методами Эйлера и Милна
Автор работы: Пользователь скрыл имя, 28 Октября 2012 в 23:52, курсовая работа
Краткое описание
Целью данной курсовой работы является углубленное рассмотрение возможностей численного решения дифференциальных уравнений. В задачи работы входит изучение методов Эйлера и Милна и рассмотрение примеров решений данными методами обычного дифференциального уравнения первого порядка.
Содержание
Год написания 2011 г., кол-во страниц: 50 стр.
Введение
1. Задача Коши для обыкновенного дифференциального уравнения первого порядка
1.1. Постановка задачи Коши.
1.2. Разрешимость задачи Коши.
2. Классификация приближенных методов решения ОДУ с начальными условиями
3. Метод Эйлера – разные подходы к построению
3.1. Геометрический способ.
3.2. Применение формулы Тейлора.
3.3. Разностный способ.
3.4. Квадратурный способ
4. Несколько простых модификаций метода Эйлера
4.1. Неявный (обратный) метод Эйлера
4.2. Неявный метод Эйлера-Коши (метод трапеций)
4.3. Метод Эйлера-Коши (метод Хойна)
4.4. Метод Эйлера-Коши с итерационной обработкой
4.5. Уточненный метод Эйлера
Пример 1.
5. Исправленный метод Эйлера
6. Пошаговый контроль точности
Пример 2.
7. Методы прогноза и коррекции. Метод Милна
Пример 3.
8. Системы дифференциальных уравнений первого порядка Дифференциальные уравнения высших порядков
Заключение
Список используемой литературы
Прикрепленные файлы: 1 файл
Курсовая.docx
- Метод Эйлера – разные подходы к построению
Рассмотрим несколько способов вывода метода Эйлера для решения ОДУ. При этом будем считать, что вычисления проводятся с расчетным шагом
расчетными точками (узлами) служат точки
промежутка и целью является построение таблицы
приближенных значений решения задачи (2.1)–(2.2) в расчетных точках .
Отметим, что все рассматриваемые численные процессы решения задачи Коши для ОДУ, и в частности, метод Эйлера, являются шаговыми методами (являясь итерационными лишь по форме), в которых на каждом шаге выполняются однотипные действия; при этом уточнения решения (характерного для итерационных методов) здесь не происходит.
Пользуясь тем, что в точке известно и значение решения (согласно (2.2)), и значение его производной (согласно (2.1)), можно записать уравнение касательной к графику искомой функции
При достаточно малом шаге ордината
этой касательной, полученная подстановкой в правую часть (3.1) значения , по непрерывности должна мало отличаться от ординаты решения задачи (2.1)–(2.2). Следовательно, точка пересечения касательной (3.1) с прямой может быть приближенно принята за новую начальную точку. Через эту точку снова проведем прямую
которая уже приближенно отражает поведение касательной к в точке . Подставляя сюда , иначе, пересекая эту «касательную» прямой , приближение значения значением
и т.д. В итоге этого процесса, определяемого формулой
и называемого (явным) методом Эйлера, график решения данной задачи Коши (2.1)–(2.2) приближенно представляется ломаной, составленной из отрезков приближенных касательных (рис. 1), откуда происходит другое название метода (3.3) – метод ломанных [2].
Из геометрической интерпретации метода Эйлера видно, что с уменьшением шага увеличивается точность расчетов, а следовательно и конечного результата.
Описываемый здесь способ вывода метода Эйлера тесно связан с предыдущим. Линеаризуя решение в окрестности начальной точки по формуле Тейлора, имеем
Отсюда при получаем
Точное равенство (3.4), переписанное в виде
говорит о том, что здесь мы имеем одновременно как саму формулу Эйлера для вычисления значения , так и ее остаточный член
где – некоторая точка интервала .
Остаточный член (3.5) характеризует локальную (или, иначе, шаговую) ошибку метода Эйлера, т. е. ошибку, совершаемую на одном шаге. Очевидно, что от шага к шагу, т. е. при многократном применении формулы (3.3), возможно наложение ошибок. За шагов, т. е. в точке , образуется глобальная ошибка.
Известный факт: порядок глобальной ошибки (относительно шага ) на единицу ниже, чем порядок локальной ошибки, а порядком глобальной ошибки и определяется порядок соответствующего численного процесса решения задачи Коши.
Таким образом, локальная ошибка метода Эйлера, согласно (3.5), есть , глобальная — , т.е. метод Эйлера относится к методам первого порядка (т.е. имеет первый класс точности). Это означает, что если, например, уменьшить шаг в 10 раз (на порядок), точность результата повысится тоже в 10 раз (на один порядок) [2].
Рассматривая уравнение (2.1) в точке , с учетом (2.2) имеем равенство
Применяя к его левой части аппроксимацию производной правым разностным отношением первого порядка точности
что идентично равенству (3.4), поставляющему формулу для вычисления вида (3.2) и локальный остаточный член (3.5). Ясно, что для получения общей расчетной формулы (3.3) можно было сразу применить аппроксимацию по формуле
заменив неизвестное точное значение известным приближенным значением .
Порядок получающегося таким способом метода численного интегрирования дифференциальной задачи (2.1)–(2.2) совпадает с порядком аппроксимации производной в левой части уравнения (2.1) [2].
Проинтегрируем левую и правую части уравнения (2.1) в границах от до :
Отсюда, с учетом того, что одной из первообразных для служит , получаем
или, с использованием начального условия (2.2),
Таким образом, данное дифференциальное уравнение (2.1) с начальным условием (2.2) преобразовалось в интегральное уравнение. При из него получится равенство
Применение к интегралу в правой части равенства (3.7) простейшей (одноточечной) формулы левых прямоугольников, имеющей в общем случае вид
дает приближенную формулу
правая часть которой, очевидно, совпадает с выражением (3.2) для подсчета значения . В общем случае расчетная формула (3.3) метода Эйлера получается численным интегрированием посредством простейшей формулы левых прямоугольников в равенстве
в предположении, что на каждом i-ом шаге в роли начальной точки выступает точка . Зная точность используемой в (3.8) квадратурной формулы, легко прийти к тому же выражению локальной ошибки метода Эйлера, что и при других способах его построения [2].
- Несколько простых модификаций метода Эйлера
Разовьем последний из подходов к построению метода Эйлера. Очевидно, применение к интегральному равенству (3.8) других простейших квадратурных формул будет порождать новые методы численного интегрирования задачи Коши (2.1)–(2.2).
Если в (3.8) использовать простейшую квадратурную формулу правых прямоугольников
придем к методу
Этот метод называется неявным (или обратным) методом Эйлера, поскольку для вычисления неизвестного значения по известному значению требуется решать уравнение, в общем случае нелинейное. Данный метод, также как и явный метод Эйлера (3.3), является методом первого порядка.
- Неявный метод Эйлера-Коши (метод трапеций)
Применение к интегралу в (3.8) простейшей квадратурной формулы трапеций, имеющей в общем случае вид
приводит тоже к неявному методу
который называется неявным методом Эйлера-Коши или методом трапеций. Квадратурная формула трапеций, как известно, на порядок точнее формул правых и левых прямоугольников. Отсюда вытекает более высокий (на единицу) порядок точности метода трапеций (4.2) по сравнению с явным и неявным методами Эйлера(3.3) и (4.1), т.е. метод трапеций (4.2) – это метод второго порядка.
Некоторый интерес представляет совместное применение явного метода Эйлера и неявного метода Эйлера-Коши.
По форме равенство (4.2) представляет собой скалярную задачу о неподвижной точке относительно неизвестного значения . Поэтому, если в правую часть (4.2) подставить хорошее начальное приближение , подсчитываемое по формуле (3.3), то тогда само это равенство можно считать шагом метода простых итераций для уточнения этого значения. Таким образом, получаем гибридный метод
который называют (явным) методом Эйлера-Коши или методом Хойна (или Хьюна[5]). Данный метод имеет второй порядок точности.
- Метод Эйлера-Коши с итерационной обработкой
Можно достичь большей точности, если, исходя из того же начального приближения
сделать не одну, а несколько итераций по методу трапеций:
Такой вариант совместного применения метода Эйлера и метода трапеций называют (усовершенствованным) метом Эйлера-Коши с итерационной обработкой (или, иначе, методом Эйлера с пересчетом). Делать много итераций по формуле (4.4) не рекомендуется (обычно их выполняют не более трех-четырех). Совпадение определенного числа разрядов в полученных числах и говорит о точности, с которой решено методом простых итераций уравнение (4.2) относительно , а вовсе не о том, что с такой точностью найдено значение . Данный метод имеет второй порядок точности.
Что бы получить следующую модификацию метода Эйлера проинтегрируем уравнение (2.1) по отрезку . Имеем
откуда следует равенство
Применяя к последнему интегралу одноточечную квадратурную формулу средних прямоугольников, имеющую в общем случае вид
и заменяя значения и известными приближенными значениями и соответственно, из (4.5) выводим метод для подсчета приближенного значения
который называется уточненным методом Эйлера [3].
Как известно, квадратурная формула прямоугольников (средней точки) имеет тот же порядок точности, что и квадратурная формула трапеций, так что уточненный метод Эйлера (4.6) также является методом второго порядка. Подтверждением этого факта может служить вывод метода (4.6) на разностной основе. Применив к равенству (3.6) формулу симметричной аппроксимации второго порядка точности, получим
откуда после приближенной замены
Другие названия этого метода: метод Нистрёма (Нюстрема) второго порядка, метод Милна второго порядка.
Обратим внимание на одно принципиальное отличие метода (4.6) от всех других рассмотренных до этого момента методов: метод (4.6) является двухшаговым. Здесь для вычисления значения привлекаются два предыдущих значения и . Двухшаговость накладывает определенные ограничения, по крайней мере, на начало численного процесса: значение не может быть найдено непосредственно этим методом с тем же шагом . Поэтому недостающую вторую начальную для процесса (4.6) точку приходится получать другим путем, например, явным методом Эйлера, а чтобы не сделать сразу большой ошибки, рекомендуется осуществлять постепенное вхождение в процесс (4.6). Так, «разгон» можно выполнить по формулам
а далее уже переключаться на счет по формуле (4.6)
Дано уравнение с начальным условием . Найдем приближенное значение решения в точке методом Эйлера и несколькими его модификациями, принимая (т.е. за два шага).
Для начала, найдем точное решение данного линейного уравнения. Для этого сделаем замену:
Для нахождения данного интеграла используем метод интегрирования по частям, используя формулу
Принимая во внимание начальное условие , имеем:
Отсюда можем найти точное значение решения в точке (обозначим его )
Теперь проведем подсчет приближенных значений решения
Явный метод Эйлера (3.3)
Начинаем процесс вычислений
Достигли нужной точки, процесс вычислений закончен.
Занятие № 22. Метод Милна четвертого порядка
Цель — ознакомить студентов с методом Милна четвертого порядка решения задачи Коши для обыкновенных дифференциальных уравнений.
Рассмотрим еще один широко известный метод прогноза и коррекции — метод Милна.
Для вывода первой формулы Милна (т.е. формулы предсказания) проинтегрируем данное уравнение (1) на промежутке [xi-3, xi+1] и в полученном интегральном равенстве
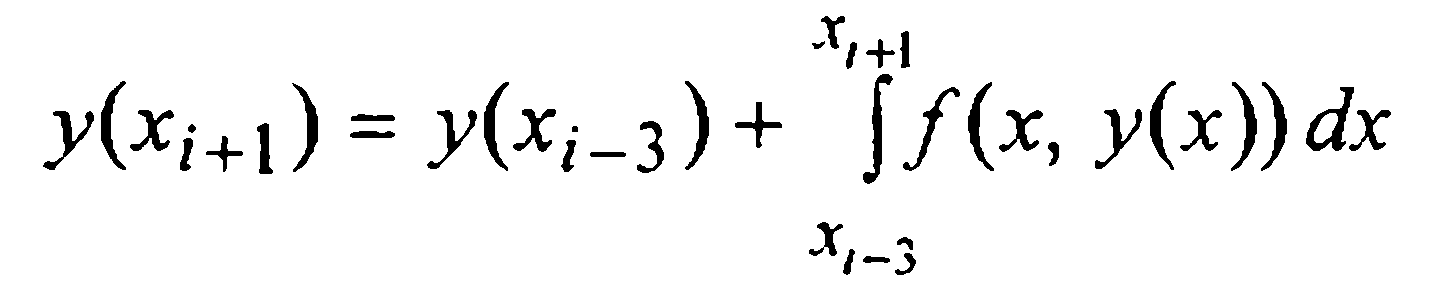
подынтегральную функцию f(x,у(х)) заменим первым интерполяционным многочленом Ньютона Р3(х), построенным по четырем узлам 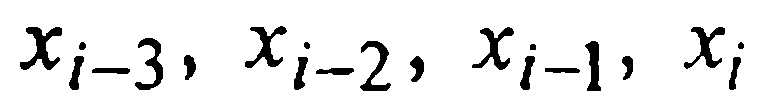
Тогда, после замены переменной 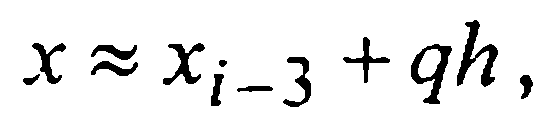
Отсюда, выразив конечные разности через значения функции, получаем первую формулу Милна (предсказания)
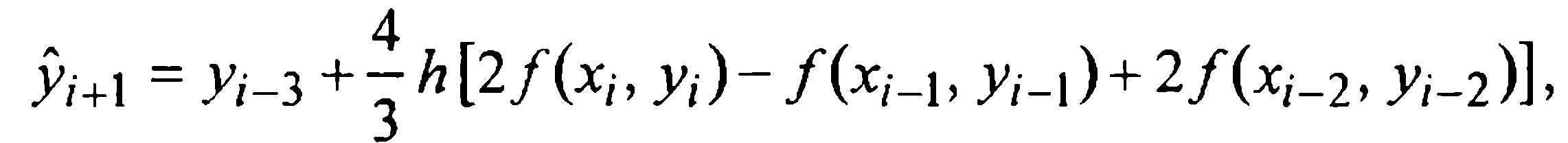
которую, очевидно, следует отнести к экстраполяционным.
Главный член локальной погрешности формулы (27) находим интегрированием следующего (первого из неучтенных) слагаемого интерполяционного многочлена Ньютона. Именно:
Считая четвертые разности примерно одинаковыми, опустим индекс у функции f в записи 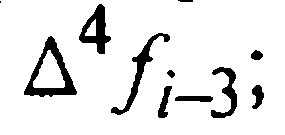
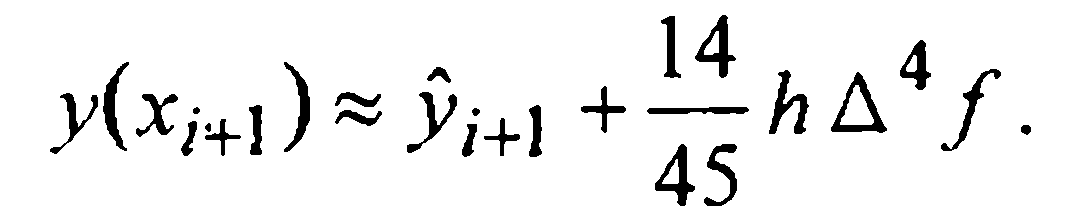
Вывод второй формулы Милна более прост. Проинтегрируем уравнение (1) теперь на промежутке [xi-1, xi+1] и в полученном равенстве
применим к интегралу простейшую формулу Симпсона. Имеем
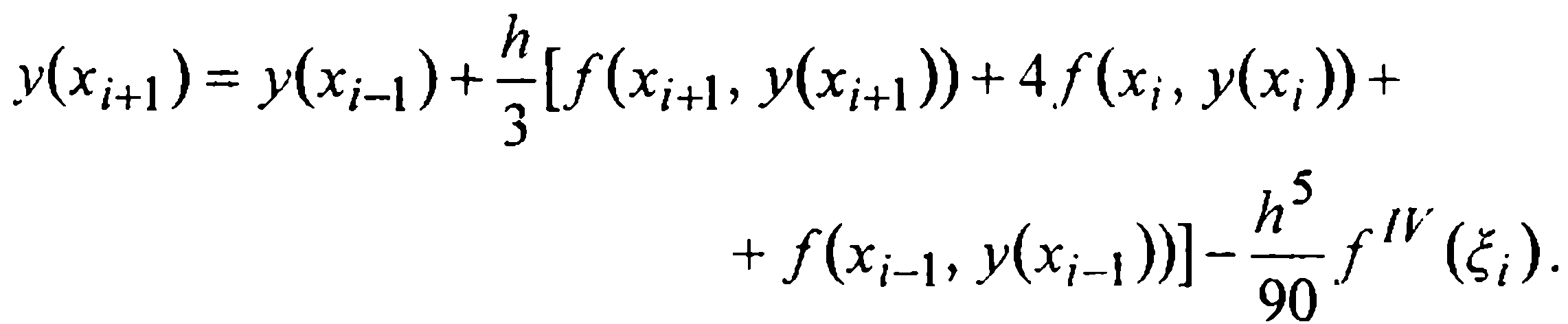
Отбрасывая здесь остаточный член и заменяя значения решения y(xi-1) и y(xi😉 известными приближенными значениями yi-1 и yi, а стоящее в правой части под знаком функции f неизвестное значение у(хi+1) тем значением 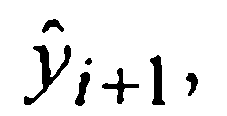
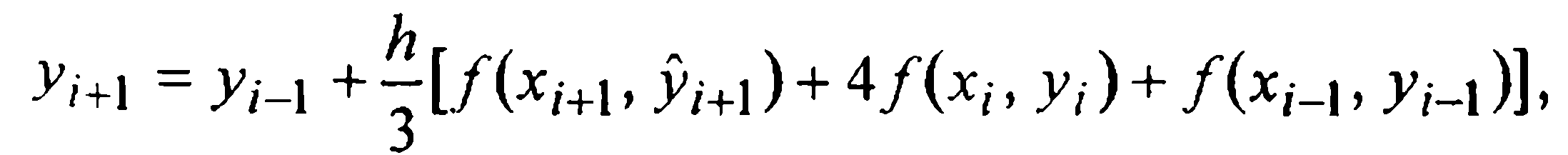
Для вывода приближенной оценки шаговой погрешности воспользуемся приближенным равенством 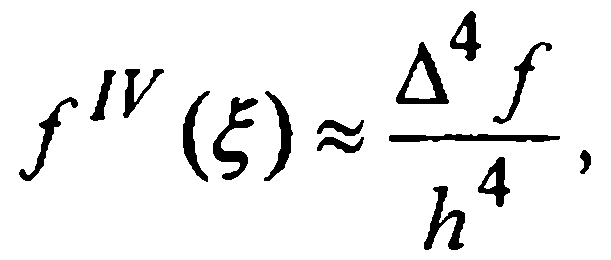
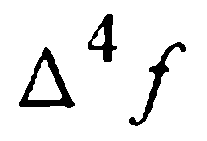

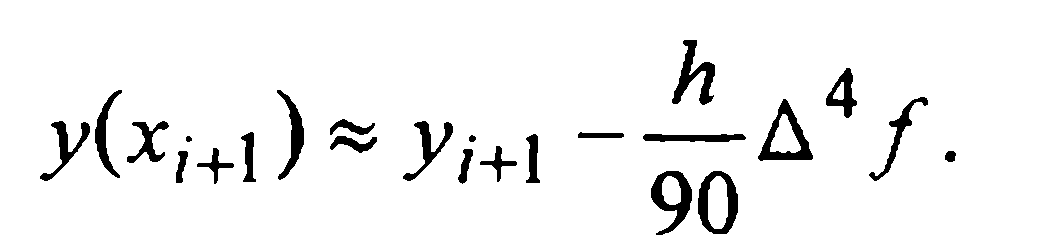
Сравнение (28) и (31) дает:
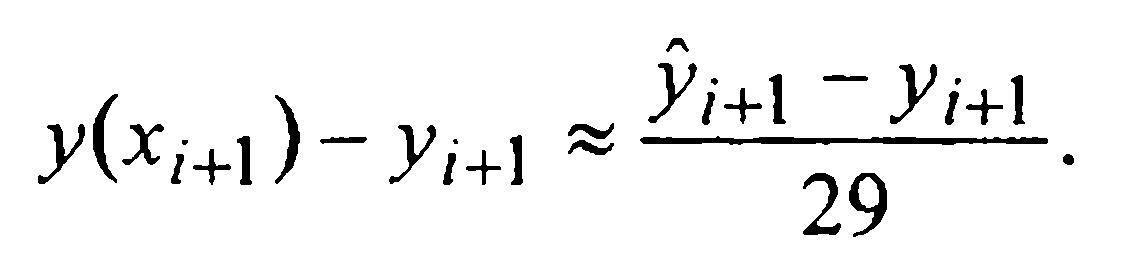
Таким образом, при численном интегрировании начальной задачи (1)-(2) методом Милна четвертого порядка, определенным формулами (27) и (30), на каждом i-м шаге следует вычислять величину
и сравнивать ее модуль с величиной ε > 0 допустимой шаговой погрешности. Если 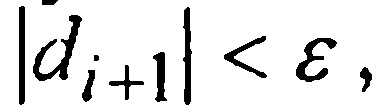
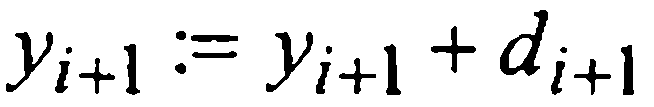
Фигурирующая в приближенном равенстве (32) постоянная 1/29 примерно вдвое меньше постоянной 19/270≈1/14 в аналогичном равенстве (24) для предиктор-корректорного метода Адамса четвертого порядка (22), что характеризует метод Милна как несколько более точный при одинаковых вычислительных затратах.
Приложение 1
Полиномы Лежандра являются специальными функциями, которые применяются при решении многих теоретических и прикладных задач. Полином Лежандра n-й степени можно определить с помощью производной n-го порядка следующим образом:
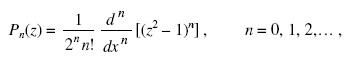
где z — комплексная переменная.
В данном учебном пособии рассматриваются и используются полиномы Лежандра для действительного аргумента x, лежащего в интервале x∈[-1, 1].
С помощью определения (1) легко получить явные выражения полиномов Лежандра действительного аргумента низших степеней:
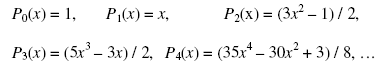
Графики перечисленных полиномов приведены на рис.1.
Все полиномы Лежандра Pn(x) имеют следующие граничные значения:
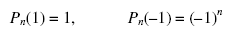
Нетрудно убедиться, что полиномы Лежандра четной степени являются четными функциями и наоборот.
Важным для практических применений является свойство ортогональности полиномов Лежандра:
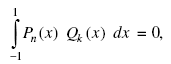
где Qk(x) — любой полином степени k, меньшей n (k
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
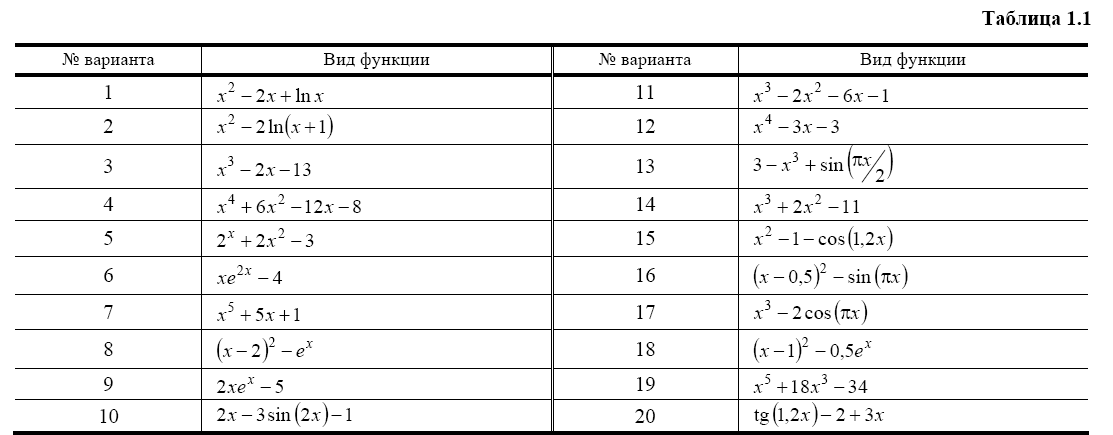
2. Ознакомьтесь с методами приближенного вычисления корней уравнений. Найдите один действительный корень уравнения с точностью 10 -5 . В ходе решения осуществить следующие шаги:
2.1. Отделить корень уравнения.
2.2. Вычислить с помощью программы значение отдельного корня методами: деление отрезка пополам, хорд, касательных, комбинированным методом, методом итераций. При использовании метода простых итераций найти решение при разных начальных приближениях. Результаты вычислений занести в таблицу.
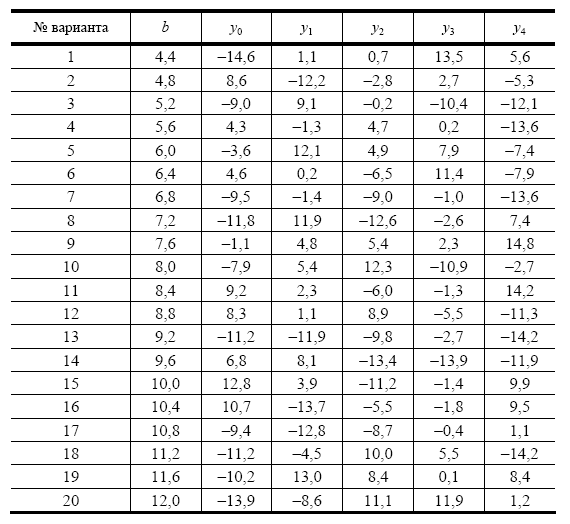
Вариант задания выбрать из табл. 1.1.
3. Найдите действительный корень уравнения с точностью 10 -4 , на интервале [a,b]. На первом этапе решения методом деления пополам, уменьшать интервал, содержащий корень, до тех пор, пока его длина не станет меньше 0,2. Потом, применить один из «более» быстрых методов.
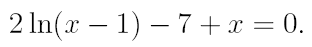 | 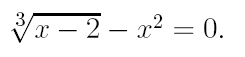 |
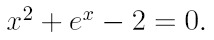 | 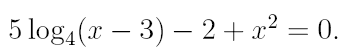 |
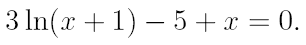 | 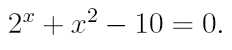 |
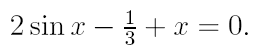 | 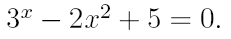 |
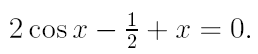 |  |
 | 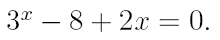 |
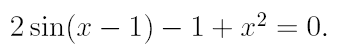 |  |
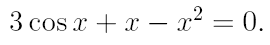 | 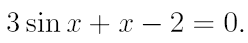 |
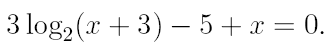 | 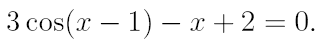 |
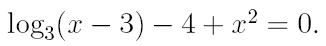 | 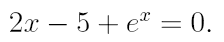 |
Отчет должен содержать:
1. График исследуемой функции с интервалами отделения корней.
2. Таблицы пошаговых расчетов корня уравнения.
3. Обоснованное заключение о преимуществах и недостатках использования исследованных методов решения применительно к заданному уравнению (для задания 1).
4. Используя схему Гаусса (схема единственного деления и схема полного выбора) решить систему уравнений
5. Решить систему уравнений двумя способами — методом итераций и методом Зейделя. Продолжать итерации до тех пор, пока точность приближенного решения не станет меньше 0,01.
Индивидуальное задание №2.
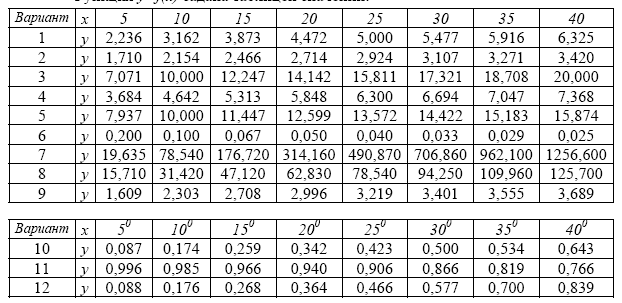
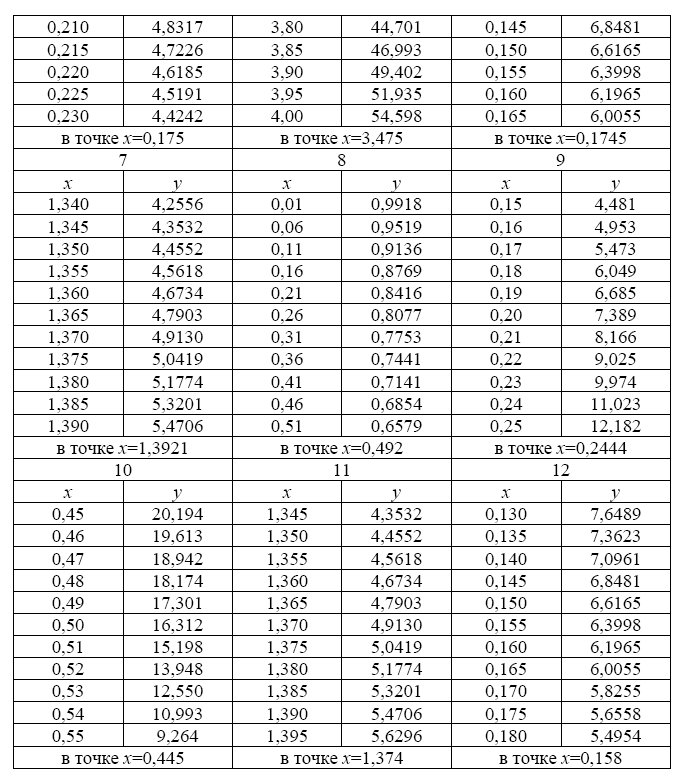
1. Функция y=f(x) задана таблицей значений:
Указания. Для вариантов 10 — 12 значения аргумента x предварительно перевести из градусов в радианы.
Даны контрольные значения аргумента x1=12; x2=26; x3=42.
a) Написать подходящие для приближенного вычисления значений y1=f(x1), y2=f(x2), y3=f(x3) интерполяционные многочлены Лагранжа первой и второй степени. Получить эти значения.
b) Составить алгоритм и написать программу на языке высокого уровня, реализующую схему Эйткена вычисления с максимально возможной точностью значения y=f(x) в произвольной точке x промежутка 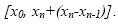
c) Сделать анализ результатов заданий 1, 2.
2. Для заданной таблично функции построить все возможные интерполяционные многочлены Ньютона максимальной степени, пригодные для определения значения функции в указанных промежуточных точках 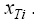
3. Вычислить значения данной функции и ее прозводной с помощью интерполяционного полинома Лагранжа Ln(x). В качестве узлов интерполяции взять:
1) равномерно распределенные точки на отрезке [a; b];
2) чебышевский набор узлов на отрезке [a; b].
При табулировании функции вычислять ряд с точностью 10 -6 .
Замечание. При вычислении ряда 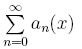
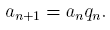
4. Найти приближенные значения функции при данных промежуточных значениях аргумента с помощью кубического сплайна и визуализируйте результаты сплайн-интерполяции.
Отчет должен содержать:
ü постановку задачи и исходные данные;
ü описание методов решения;
ü графики, полученных интерполяционных многочленов;
ü листинг программы.
Индивидуальное задание №3
1. Используя данные таблицы 1, вычислить производную указанной функции в точке х (точка х не является узлом таблицы)
2. Используя данные таблицы 1, вычислить производную указанной функции в точке х (точка х – узел таблицы)
Таблица 1.
| Вариант | Задание 1. | Задание 2. | ||
| Таблица № | х | Таблица № | х | Используемая формула |
| 3.0 | 2 (взять 5 последних значений) | 5,3 | Лагранжа | |
| 3.5 | 3 (взять 4 последних значения) | 6,7 | Лагранжа | |
| 2.5 | 2,6 | Ньютона | ||
| 5.8 | -3,2 | Ньютона | ||
| 3.1 | 2,3 | Ньютона | ||
| 3.9 | 2,1 | Ньютона | ||
| 3.3 | 4 (взять 5 первых значений) | -0,8 | Лагранжа | |
| 6.0 | 5 (взять 4 первых значения) | 3,8 | Лагранжа | |
| 3.2 | 2 (взять 5 первых значений) | 2,9 | Лагранжа | |
| 5.3 | 1,6 | Ньютона | ||
| 3.9 | 3,4 | Ньютона | ||
| 7.2 | 5 (взять 4 первых значения) | Лагранжа | ||
| 4.4 | 6,2 | Ньютона | ||
| 3.6 | 3 (взять 5 последних значений) | 4,5 | Лагранжа | |
| 2.2 | 4 (взять 5 последних значений) | Лагранжа | ||
| 6.8 | 3,7 | Ньютона | ||
| 3.4 | 5,6 | Ньютона | ||
| 3.7 | 4 (взять 4 последних значения) | 6,4 | Лагранжа | |
| 1.8 | 5 (взять 5 первых значений) | 7,4 | Лагранжа | |
| 7.6 | 4,5 | Ньютона |
Таблица 2.
| Таблица 3.
| ||||||||||||||||||||||||||||||||
Таблица 4.
| Таблица 5.
|
3. Вычислить значения интеграла, используя квадратурные формулы:
· Гаусса с двумя узлами.
Интеграл вычислить с точностью ε=10 -6 . Точность вычисления интеграла определяется сравнением результатов при различном числе разбиений отрезка интегрирования. Именно, точность ε считается достигнутой, если
здесь 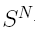
Отчет должен содержать:
· постановку задачи и исходные данные,
· описание методов решения и расчетные формулы,
· таблицы значений интегралов с указанием числа разбиений, потребовавшихся для достижения заданной точности,
1. 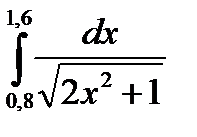

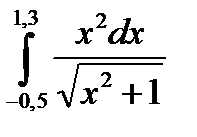
5. 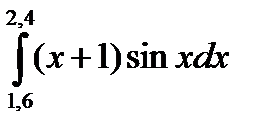
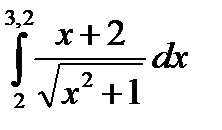

9. 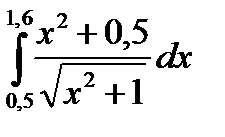
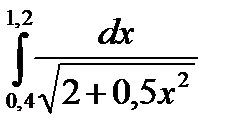
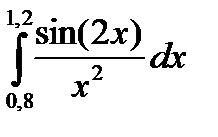
13. 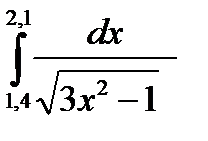
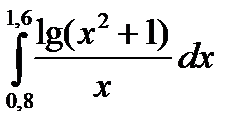

17. 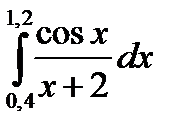
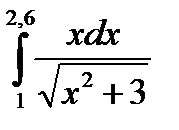

Литература
1. Бахвалов Н. С. Численные методы: учеб. пособие для вузов/ Н. С. Бахвалов, Н. П. Жидков, Г. М. Кобельков. — 4-е изд.; Гриф МО. — Москва: БИНОМ. Лаборатория знаний, 2006. — 636 с. — (Классический университетский учебник). — Библиогр.: с. 624-628. — Предм. указ.: с. 629-632.
2. Вержбицкий В. М. Численные методы: Линейная алгебра и нелинейные уравнения: учеб. пособие для вузов / В. М. Вержбицкий. — 2-е изд., испр.; Гриф МО. — Москва: ОНИКС 21 век, 2005. — 431 с.: ил. — Библиогр.: с. 419-424. — Предм. указ. с. 425-429.
3. Демидович Б. П. Численные методы анализа: приближение функций, дифференциальные и интегральные уравнения: учеб. пособие / Б. П. Демидович, В. А. Марон, Э. З. Шувалова; под ред. Б. П. Демидовича. — Изд. 4-е, стер. — Санкт-Петербург: Лань, 2008. — 400 с. — (Классическая учебная литература по математике). — Библиогр. в конце гл.
4. Киреев В. И. Численные методы в примерах и задачах: учеб. пособие для вузов/ В. И. Киреев, А. В. Пантелеев. — Изд. 2-е, стер.; Гриф УМО. — Москва: Высш. шк., 2006. — 480 с.: ил. — (Прикладная математика для ВТУЗов). — Библиогр.: с. 477-480 .
5. Пантина И. В. Вычислительная математика [Электронный ресурс] учебник для вузов/ И. В. Пантина, А. В. Синчуков. — 2-е изд., перераб. и доп. — Москва: Синергия, 2012. — 175 с.
6. Пирумов У. Г. Численные методы: учеб. пособие для вузов/ У. Г. Пирумов. — 2-е изд., испр. и доп.; гриф МО. — Москва: Дрофа, 2003. — 221 с.: ил. — (Высшее образование). — Библиогр.: с. 216. — Имен. указ.: с. 217.
7. Срочко В. А. Численные методы: курс лекций / В. А. Срочко. — Гриф УМО. — Санкт-Петербург [и др.]: Лань, 2010. — 202 с. — Библиогр.: с. 200.
8. Турчак Л. И. Основы численных методов: учеб. пособие / Л. И. Турчак, П. В. Плотников. — Изд. 2-е, перераб. и доп.; Гриф МО. — Москва: ФИЗМАТЛИТ, 2005. — 300 с.: ил. — Библиогр.: с. 290-292. — Прил.: с. 286-289. — Предм. указ.: с. 293-300.
9. Шевцов Г. С. Численные методы линейной алгебры: учеб. пособие для мат. напр. и спец. / Г. С. Шевцов, О. Г. Крюкова, Б. И. Мызникова. — Гриф УМО. — Москва: Финансы и статистика: ИНФРА-М, 2008. — 479 с. — (Финансы и статистика). — Библиогр.: с. 473-474. — Предм. указ.: с. 475-479.
http://www.referat911.ru/Matematika/reshenie-differencialnyh-uravnenij-metodami-jejlera/39750-1324339-place2.html
http://lektsii.org/2-84243.html
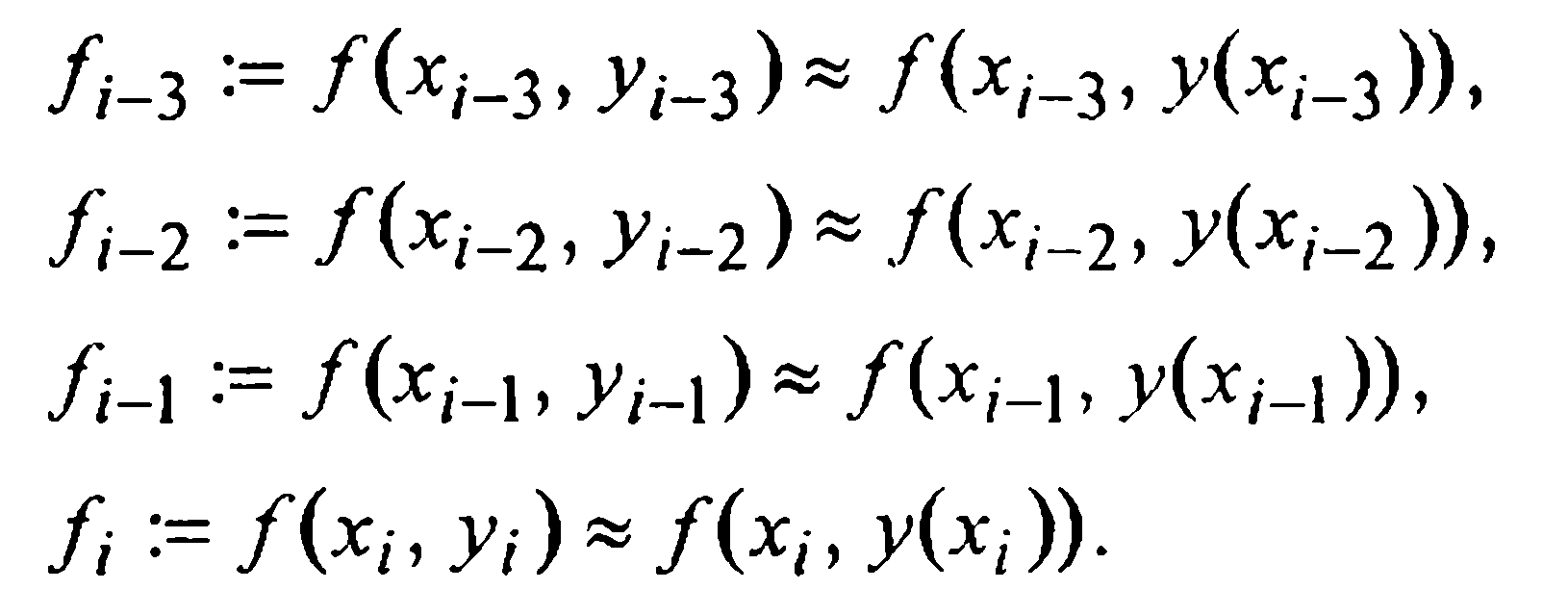
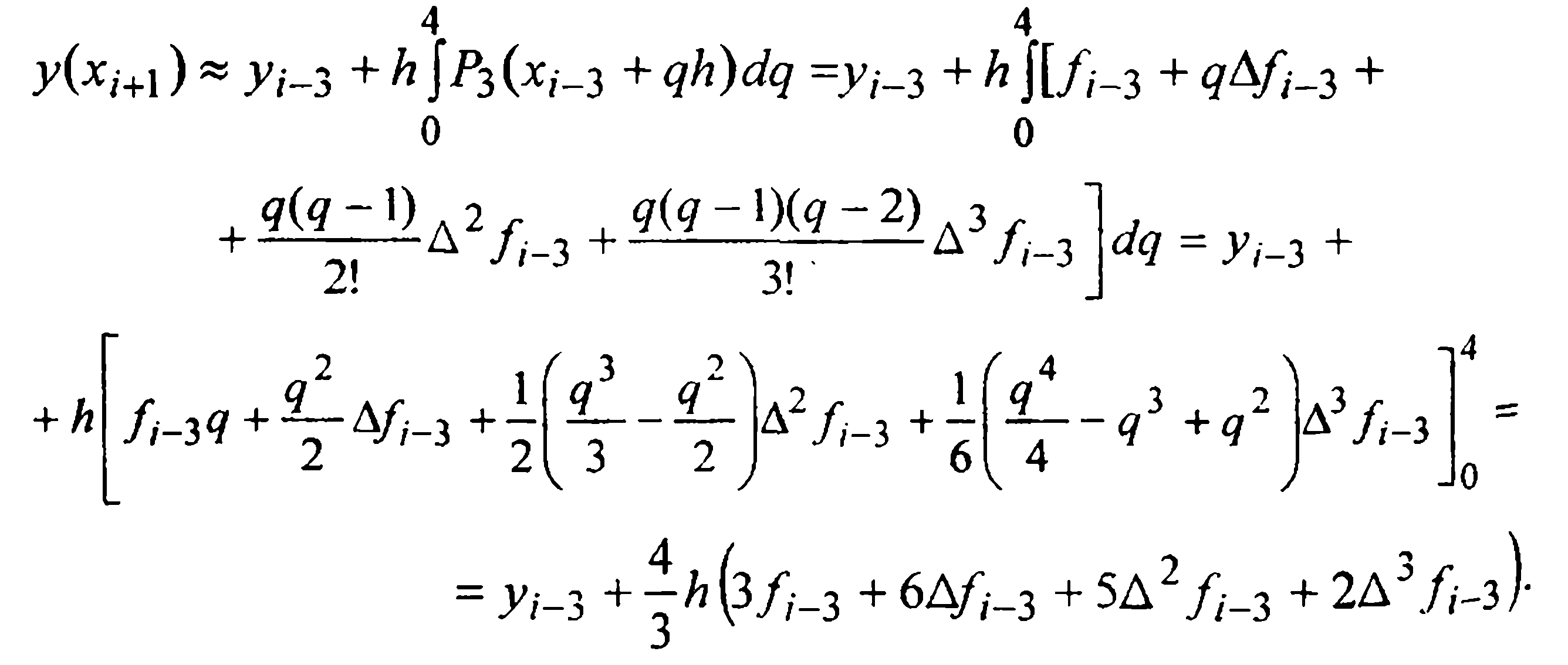
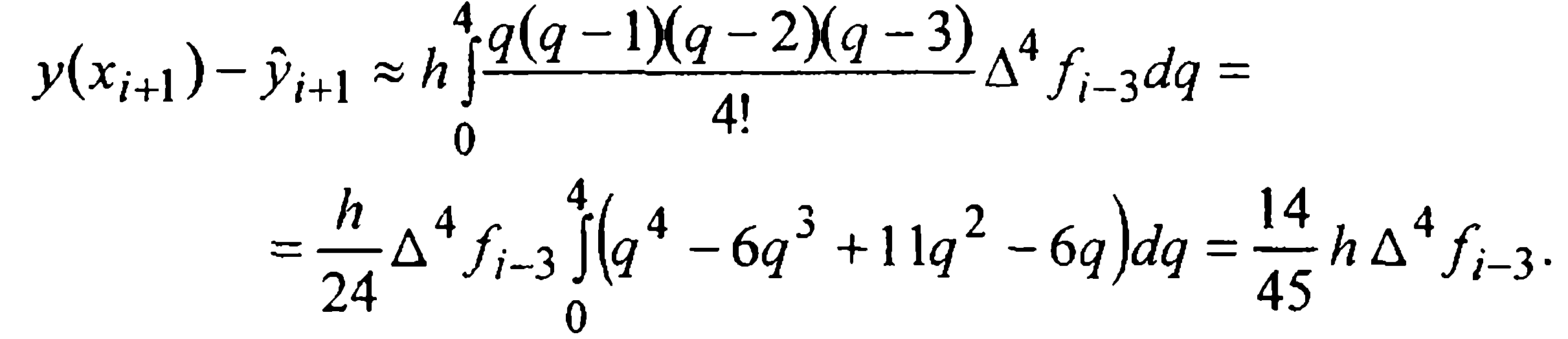
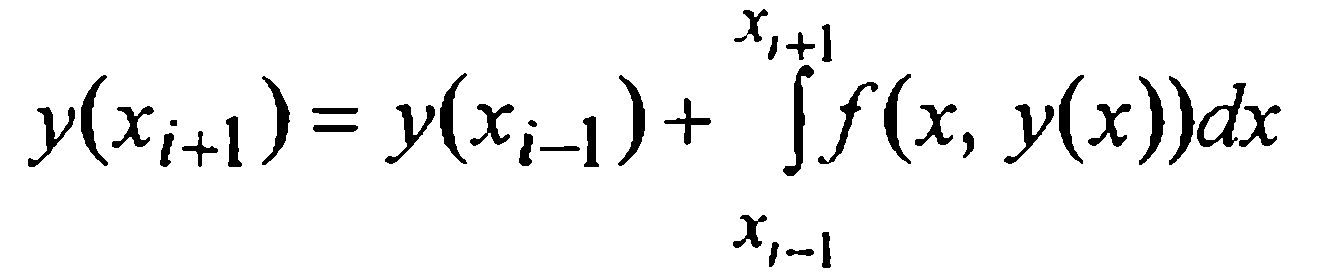
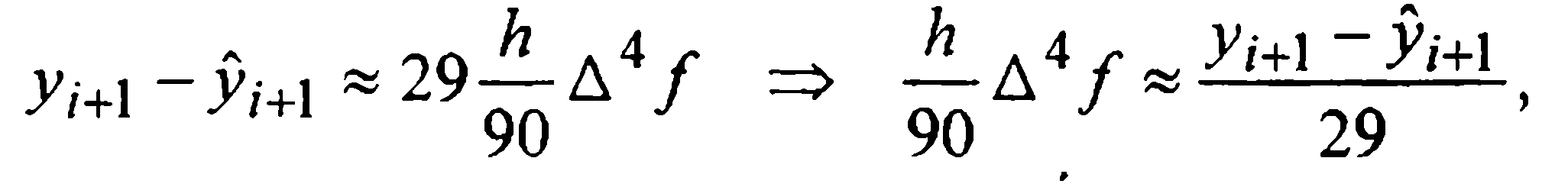
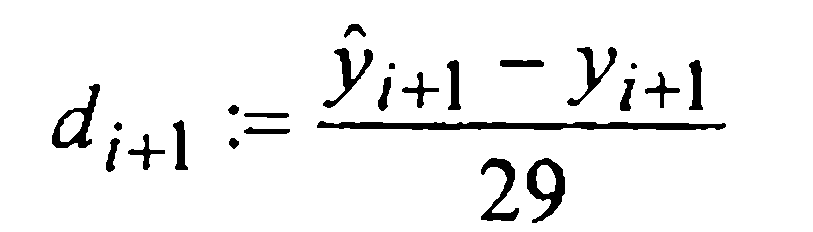




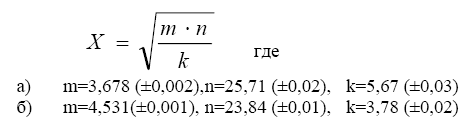

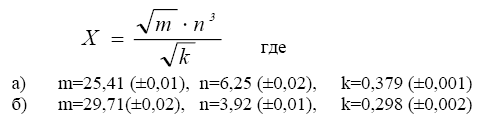
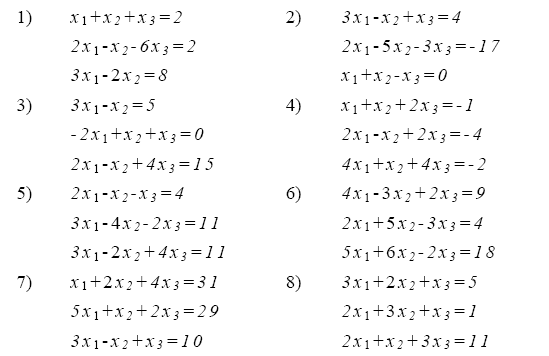
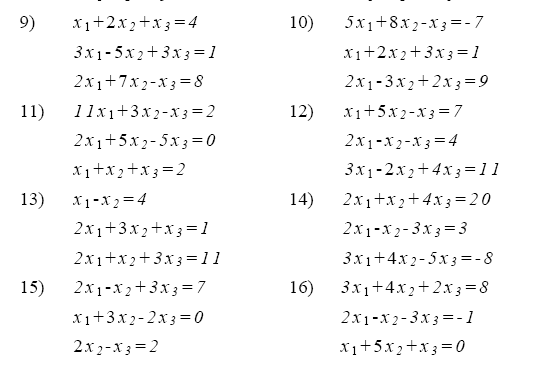
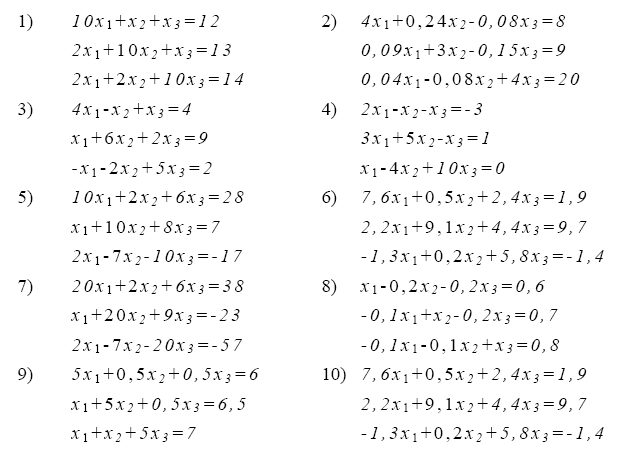

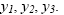

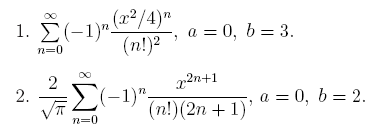
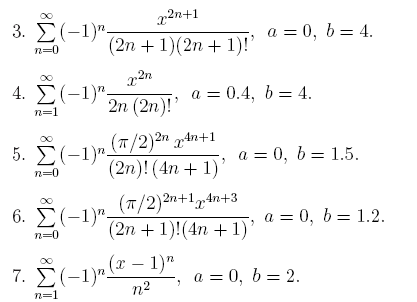
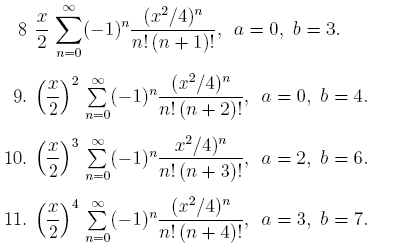

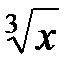 -cos(0,4-0,7x)
-cos(0,4-0,7x)